基于SVD的地铁盾构洞门钢环空间形态参数计算
张广龙, 吴继忠
(1. 昆山市中建项目管理有限公司, 江苏 昆山 215300; 2. 南京工业大学测绘科学与技术学院, 江苏 南京 211800)
0 引言
在我国当前地铁隧道建设中,盾构法兼顾了施工安全、高效、复杂地层适应性和地表沉降控制等要求,已成为主流工法和机械化施工的典范[1]。在盾构法施工中,盾构的始发和接收位置均要设置洞门钢环。作为盾构掘进的起始和终止位置,洞门钢环安装后的中心位置与设计值的偏差须在允许范围内。洞门钢环为圆环形,由于直径较大,为便于运输,通常由若干分块拼接而成,盾构的始发和接收均从洞门钢环内穿过。为确保盾构按照设计路线掘进,在洞门钢环安装完成后,需要获取洞门钢环的圆心位置、平整度、垂直度、圆度等空间形态参数,再与设计值进行比较。但上述空间形态参数不能直接测得,只能先通过测定洞门钢环上若干个离散点的三维坐标后,再进行数据拟合间接得到。
安装后的洞门钢环是一个空间圆,本质上是空间平面与球面的相交线。已有的数据处理方法总体上可以分为如下3种: 1)直接用最小二乘法原理列出观测方程。该方法涉及观测方程线性化和初始值选取[2-4],实际应用较为不便。2)先拟合空间平面,再将空间平面旋转,将观测点旋转到二维平面上,然后在平面上进行圆拟合得出圆心坐标和半径,最后将圆心坐标逆旋转,得到其真实三维坐标[5-6]。该计算步骤涉及2次空间向量旋转,程序较为繁琐。3)在空间平面拟合的基础上,根据空间圆圆心位于任意2个观测点连线的中垂面上的特性,由空间向量构建中垂面方程分步求解圆心坐标和半径[7-9],也可以将中垂面方程和空间平面方程联合,一步求解出空间圆参数和空间平面方程[10]; 但该方法需要未知参数的初始值,还可能涉及迭代运算。
本文在分析空间平面方程和球面方程特点的基础上,利用奇异值分解(singular value decomposition,SVD)法一次求得球面方程参数和空间平面法向量,再由上述参数直接计算洞门钢环空间形态参数; 并结合方差比值检验法剔除粗差。将该方法应用于南京地铁6号线双龙街出入线2组洞门钢环的空间形态参数计算,证明了其有效性,取得了较好的效果。
1 SVD解算球面方程及提取平面方程参数
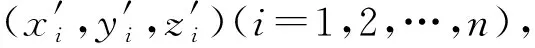
1.1 空间平面
设重心化前的空间平面方程为
ax′+by′+cz′=d。
(1)
则重心化后的平面方程为
ax+by+cz=0。
(2)
式(2)中(a,b,c)为平面的单位法向量,令
(3)
则空间平面拟合的目标函数为
‖A1X‖2=min。
(4)

‖A1X‖2=‖U1S1V1TX‖2。
(5)
由于U1是正交矩阵,式(5)可变换为

(6)
y=V1TX是单位向量,由于σ1≥σ2≥σ3,当且仅当y1=y2=0时目标函数有最小值,此时y3=±1,正负号不影响空间平面姿态。为便于表示,取y=(0,0,1)T,顾及V1正交矩阵的特点,则
X=V1y。
(7)
代入y=(0,0,1)T可知,X的值为V1的第3列。
1.2 球面
设重心化后的球面方程为:
(x-x0)2+(y-y0)2+(z-z0)2=R2。
(8)
式中: (x0,y0,z0)为球心坐标;R为半径。
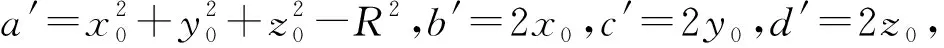
(9)
令
(10)
实际应用中观测点数n通常多于4个,则式(9)的目标函数为
‖A2X-b‖2=min。
(11)

(12)
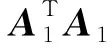
(13)

(14)
令
(15)
则有
(16)
(17)
2 洞门钢环空间形态参数计算及粗差处理
2.1 数据采集和预处理
洞门钢环上点采集一般采用无反射棱镜全站仪,观测前根据现场条件在洞门附近建立控制点或者通过全站仪自由设站方式获取设站点坐标。无论采用哪种方式均需要确保设站位置与已有控制点和洞门有较好的通视条件,实现1个测站完成1个洞门钢环所需点的采集工作,减少误差积累和产生粗差的可能性。


图1 洞门钢环及其观测点分布Fig. 1 Portal steel ring and distribution of observed points
2.2 空间形态参数计算
利用重心化后的坐标,根据式(10)构建矩阵A2和b,对A2进行奇异值分解; 根据式(12)求解球心坐标(x0,y0,z0)和半径R,从A2奇异值分解后的正交矩阵V2最后1列中提取平面单位法向量(a,b,c)。
设球心在空间平面上的投影点为(xc,yc,zc),该点即为空间圆圆心。球心到空间圆圆心的向量垂直于平面,即
(18)
式中t为直线上的任意一点到(x0,y0,z0)距离的量度。
空间圆圆心位于平面上,由式(2)和(18)得到
(19)
因此,空间圆圆心坐标为
(20)

球心到空间圆圆心的距离
(21)
空间圆半径
(22)
根据上述信息,计算各个点到平面的垂直距离Δdi和平整度m1。
(23)
计算各个点到圆周的最短距离Δri,其实质是点到圆心的距离与半径之差,再由Δri计算圆度m2。
(24)
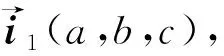
(25)
式(25)计算的是洞门钢环与XY平面之间的夹角,根据实际需要,也可以代入XZ平面或YZ平面的单位法向量,按照相同方法计算出洞门钢环与XZ平面或YZ平面的夹角。
2.3 粗差剔除方法
SVD方法不具备抵御粗差的能力,当观测数据中含有明显噪声即粗差点情况时,其估计结果必然会偏离真值。在离散点坐标采集过程中,由于施工现场环境的复杂性,有可能造成部分观测结果中有较大误差甚至粗差,有必要对误差较大的观测点加以剔除,以消除对结果的扰动。此时可通过借鉴方差比值检验法[15],其基本原理如下:
1)利用所有观测点,计算残差v和中误差σ0。
(26)

(27)
式中:α为显著性水平;r1、r2为自由度。
根据式(27)统计检验结果,确定包含粗差的观测点并将其剔除。上述过程每1轮循环剔除最大的粗差,需要循环多次,直到所有含有粗差的观测点都被剔除为止。
3 工程应用实例
3.1 数据采集
以南京地铁6号线双龙街停车场入场线和出场线的2个洞门钢环测量为例,采用免棱镜全站仪,其标称测角精度为1",测距精度为1.5 mm+1×10-6D。观测时在洞门正前方的隧道中线上设置全站仪,利用自由设站完成测站坐标计算和定向,然后直接绕洞门钢环外边缘一周采集点的三维坐标。图2示出了入场线和出场线洞门钢环重心化后的观测点。经检测,观测点中不含粗差。
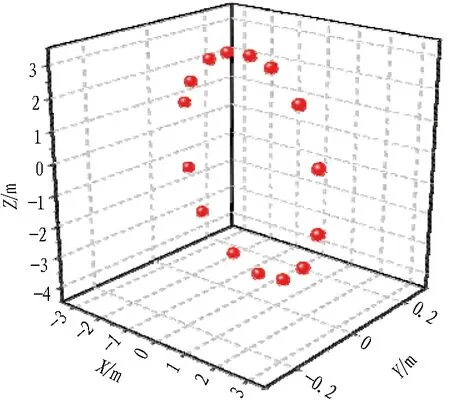
(a) 入场线洞门钢环观测点
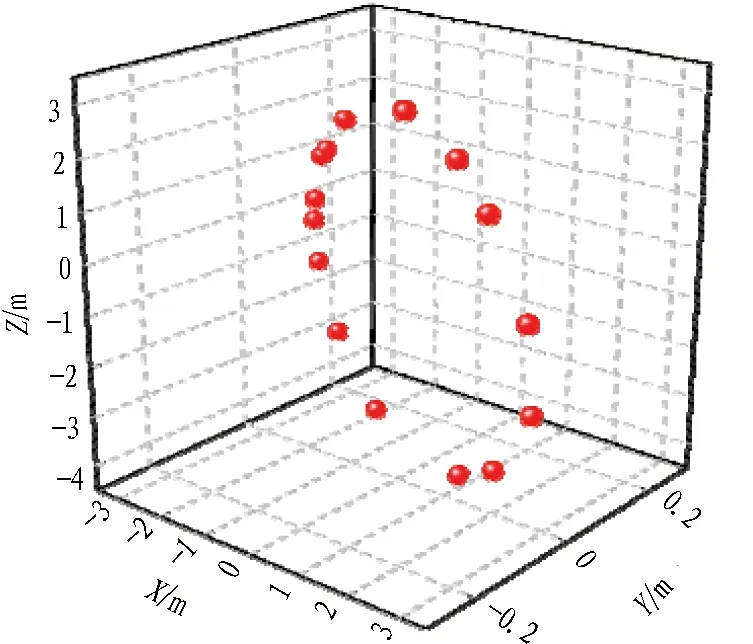
(b) 出场线洞门钢环观测点图2 洞门钢环观测点Fig. 2 Observed points on portal steel ring
3.2 数据处理结果
根据第2节描述的计算流程,利用自编软件实现了相应功能。图3示出了观测点到拟合平面和圆的距离。表1给出了洞门钢环空间形态参数计算结果,为便于比较,还同时给出了某商业软件的计算结果。

(a) 入场线洞门钢环观测点
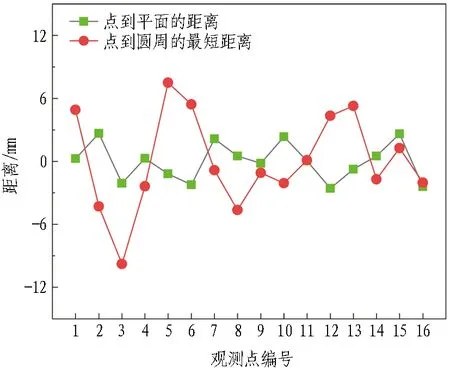
(b) 出场线洞门钢环观测点图3 观测点到拟合平面和圆的距离Fig. 3 Distances between observed points to fitting plane and circle

表1 洞门钢环空间形态参数计算结果比较Table 1 Comparison of spatial shape parameters for portal steel ring
由图3可以看出: 就入场线洞门钢环而言,各观测点到洞门钢环所在空间平面距离最大为10.8 mm,最小为-9.4 mm;各观测点到洞门钢环所在圆最短距离最大为4.9 mm,最小为-5.5 mm。就出场线洞门钢环而言,各观测点到洞门钢环所在空间平面距离最大为7.5 mm,最小为-9.8 m;各观测点到洞门钢环所在圆最短距离最大为2.7 mm,最小为-2.6 mm。出场线洞门钢环观测点总体质量优于入场线洞门钢环观测点。
从表1可以看出,采用2种不同方法计算洞门钢环空间形态参数的差异很小,洞门钢环半径和平整度的结果几乎一致,中心坐标最大差异为2 mm,圆度的最大差异的0.8 mm,对实际应用的影响可忽略不计。此外,由SVD法提取出平面的单位法向量后,可以得到洞门钢环与水平面之间的夹角,但商业软件目前未能提供该项参数。
3.3 粗差探测效果分析
为分析粗差的影响并评价粗差剔除方法的有效性,统一在每组观测点第1个点的X方向加入1 m的粗差。按照粗差剔除的流程,显著性水平取0.05,逐个剔除观测点并进行假设检验。图4示出了每次剔除1个观测点后得到的方差比值。
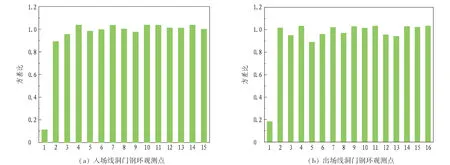
图4 逐个剔除观测点后的方差比值Fig. 4 Variance ratio after elimination of each observed point
从图4可以看出,逐个剔除第2个到最后1个观测点对应的方差比较为接近,只有第1个观测点剔除后的方差比明显小于其他结果且通过了假设检验,说明粗差定位是正确的。将各组数据的1号观测点剔除,比较粗差剔除前后空间形态参数的计算结果比较,见表2。

表2 SVD法粗差剔除前后参数计算结果比较Table 2 Comparison of calculated parameters before and after gross error elimination in SVD method
从表2可以看出,在1号观测点加入粗差后,对空间形态参数计算结果产生了一定的影响。由于2组观测点数量较多,分别有15个和16个,粗差对结果的影响不明显,对中心坐标和半径的影响最大为1.6 cm,但平整度和圆度明显增大,分别是原来的2倍和13倍左右。粗差剔除后,计算结果与表1中SVD法计算结果局部最大差异仅为1 mm,其结果可靠,说明粗差定位准确。
4 结论与讨论
在盾构始发和接收前,必须准确确定隧道洞门钢环空间形态参数,针对已有方法步骤繁琐、需要参数初始值迭代运算等不足,提出基于SVD的计算方法,结合该方法的实际应用,得出如下结论:
1)利用SVD法可以一次性解算出球面方程参数和空间平面法向量,再由上述参数直接计算洞门钢环空间形态参数,该过程无需初始值和迭代计算,步骤大大简化,SVD法与商业软件计算结果的差异可忽略不计。
2)SVD法无法抵御粗差的影响,为应对观测点中可能存在的粗差,应用方差比值检验法进行粗差探测。由于事先无法预知哪个观测点包含粗差,此时需要通过迭代的方式逐个筛选出粗差。在人为加入粗差后,利用方差比值检验可准确实现粗差定位,获得准确可靠的结果,将二者结合具有较好的应用价值。
需要注意的是,SVD法以空间平面方程和球面方程系数矩阵具有的关联性为基础,因此只适合于圆形洞门钢环的处理。对于其他类型洞门环的拟合解算还有待进一步研究。SVD法计算量较小,适用于全站仪机载程序的开发,可实现观测结果的实时输出和现场结果检核。

