S形空间曲线顶管开挖引起的地表沉降计算
——以宁波市潘桥变电站迁建工程为例
许有俊, 孟毅欣, *, 张 朝, 韩志强, 郭 飞, 高胜雷
(1. 内蒙古科技大学土木工程学院, 内蒙古 包头 014010; 2. 内蒙古科技大学 矿山安全与地下工程院士专家工作站, 内蒙古 包头 014010; 3. 内蒙古科技大学 内蒙古自治区高校城市地下工程技术研究中心, 内蒙古 包头 014010; 4. 北京市政建设集团有限责任公司, 北京 100079)
0 引言
近年来,顶管非开挖技术大量应用于城市市政管道工程建设中。受大量已有地下结构的约束,一些新建顶管工程轴线不得不采用平面曲线甚至空间曲线。与直线顶管工程相比,曲线顶管对地层的扰动更大,而由平曲线与竖曲线叠合形成的S形空间曲线顶管施工对土体的扰动更为复杂。
目前,对于直线顶管、盾构及曲线盾构施工扰动的研究成果较多。魏纲等[1]、吴修锋[2]、王日东[3]基于Mindlin弹性理论解,给出了由直线顶管开挖面正面附加应力、顶管机及后续管节的侧摩阻力引起的土体竖向位移三维计算公式。朱合华等[4]采用弹性力学薄壳理论和温克尔假设,推导了曲线顶管施工过程中管体法向和纵向变形的理论表达式,并进一步给出了地层荷载和管片内力的表达式,最后通过具体的工程实例验证其合理性。张鹏等[5]对曲线顶管的横断面沉降进行监测,发现曲线顶管施工引起的地面沉降槽曲线并不以隧洞轴线对称,最大沉降点存在一定的水平偏移,但是沉降槽的偏转方向并不是固定不变的,其偏移方向与施工参数和地层等因素相关。邓皇适等[6]、孙捷城等[7]基于镜像法及Mindlin解,对曲线盾构施工中的不对等附加推力、机头摩擦力、同步注浆压力及考虑平曲线超挖量等因素引起的地表沉降进行了计算。上述研究结果表明: 对于直线顶管、盾构隧道及曲线盾构施工引起的地表沉降的理论计算研究较多,但是对于S形空间曲线顶管施工引起的地表变形理论计算模型的研究较少,且缺乏完整的理论计算方法。
本文以宁波潘桥变电站迁建工程中的S形空间曲线顶管为研究背景,针对S形空间曲线顶进对土体扰动的因素和特点,综合考虑曲线顶管施工开挖面附加推力、顶管机机壳及后续管节的摩擦力、后续管节的同步注浆压力及顶管机转弯产生的超挖空隙对地表变形的影响,基于Mindlin解和随机介质理论构建S形空间曲线顶管地表变形计算模型,通过工程实例数据的对比验证,探究S形空间曲线顶管施工地表沉降槽偏移方向的变化规律。
1 直线与空间曲线顶管对土体扰动的区别
顶管顶进过程中,会改变周围土体的应力场,使得土体必然产生变形,同时顶管施工必然造成土体损失,二者叠加使得地表发生变形[8]。
空间曲线顶管地层损失模型如图1所示。由图可知,直线顶管施工的地层损失来源于顶管机尾部脱空产生的环形间隙(顶管机刀盘直径比后续管节的直径大4 cm左右); 空间曲线顶管施工的地层损失来源于2部分: 第1部分为顶管机尾部环形间隙,第2部分为顶管机转弯与外侧土体产生的接触间隙(特殊超挖空隙),在顶管机无超挖刀参与掘进的情况下,特殊超挖间隙出现在弯道外侧[9]。

(a) 直线顶管地层损失模型

(b) 空间曲线顶管地层损失模型图1 空间曲线顶管地层损失模型Fig. 1 Disturbance model of pipe jacking formation with spatial curve
综上所述,与直线顶管施工对周围土体的扰动过程相比,S形空间曲线顶管在掘进过程中,将产生水平、竖向特殊超挖间隙。为此,本文在直线顶管施工引起地表沉降计算方法的基础上,考虑水平、竖向特殊超挖间隙等因素,进一步推导S形空间曲线顶管施工引起的地表沉降计算方法。
2 S形空间曲线顶管施工地表沉降计算
2.1 地层损失引起的地表沉降计算
分析上述S形空间曲线顶管施工地层损失模型,采用随机介质理论来计算由于土体损失而引起的土体变形。在计算过程中考虑土体为一种“随机介质”,认为整个土体的开挖引起的地面变形是若干微小开挖单元引起地面变形的总和[10]。假定在不排水条件下最终的沉降槽体积应等于土体损失的体积,故当开挖单元完全塌落时等于单元体积dx′dy′dz′。以开挖单元中心为坐标原点,由此得到开挖单元完全塌落引起的上部土体坐标点(x,y,z)的沉降
(1)
式中r(z)为主要影响半径,r(z)=z/tanβ,β为地层主要影响角。
顶管开挖断面示意如图2所示。假设顶管机开挖完成后,后续管节进行支护,由于管径差,土体坍塌体积为管节外壁与土体间的环形区域及转弯产生的接触空隙。

图2 顶管开挖断面示意图Fig. 2 Cross-section of pipe jacking excavation
顶管机尾部环形间隙产生的地表沉降
(2)
式中:Ω为隧道超挖后断面面积;ω为顶管机断面面积;η为z轴方向的单位长度。
顶管在空间曲线段掘进过程中,对2个转弯方向的纠偏挤土效应进行分析。转弯超挖示意如图3所示。图中,水平和竖向转弯产生的接触空隙分别为δh、δv。

图3 转弯超挖示意图Fig. 3 Sketch of turning over-excavation
曲线顶管超挖量计算示意如图4所示。由顶管机曲线顶进超挖的几何关系,得顶管机转弯的特殊超挖量计算公式如下[9]:
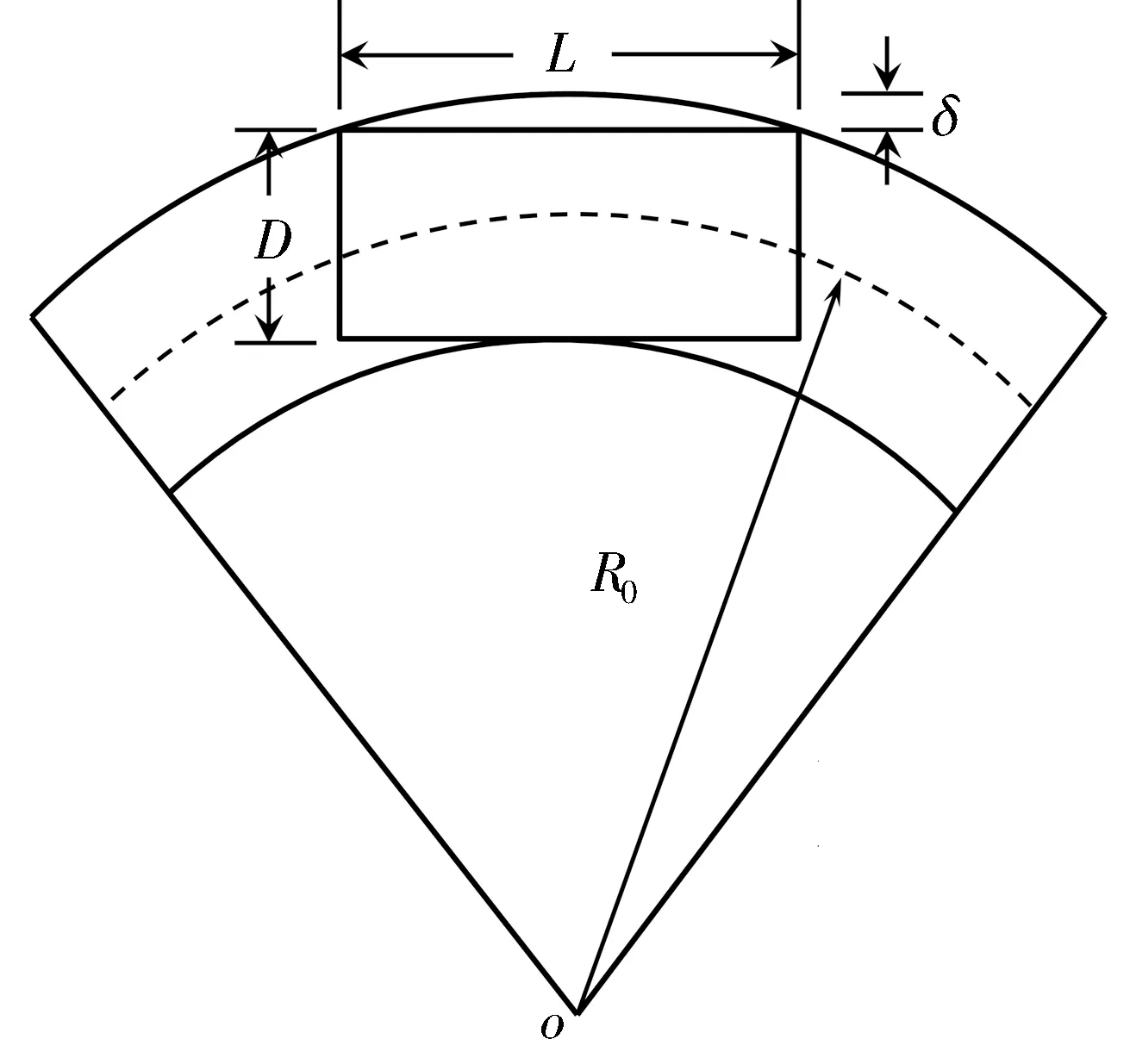
R0为曲线隧道半径; D为顶管机直径; L为顶管机长度; δ为曲线外侧超挖量。图4 曲线顶管超挖量计算示意图Fig. 4 Sketch of curved over-excavation calculation
(3)
曲线段顶进任一断面的超挖间隙面积简化为以δ等量径向增加的半环形面积,则超挖间隙面积
(4)
式中R为隧道半径。
分别计算水平和竖向超挖量所对应的接触间隙的面积为Sh和Sv,并通过式(5)计算得到水平和竖向超挖引起的沉降值分别为wover1和wover2。
(5)
2.2 施工荷载引起的地表沉降计算
本节采用Mindlin解,对顶管施工的施工荷载进行理论分析研究,计算开挖面附加推力、顶管机及管节的摩擦力和注浆压力引起的地表竖向变形。顶管掘进受力模型如图5所示。在土体掘进过程中本文做以下假定: 1)土体为线弹性半无限空间,泊松比为v,土的剪切模量为G; 2)顶管机外径D=2R,长度为L,轴线埋深为H; 3)顶管管节外半径Rg,单节长度为l=1.5 m,管节触变泥浆注浆计算长度为E; 4)开挖面附加推力为q′,作用面为与顶管机机头直径相同的圆形; 5)顶管机外壳摩擦力f沿顶管机外壳均匀分布; 6)顶管管节摩擦力f1沿顶管管节均匀分布; 7)触变泥浆注浆压力p沿顶管机外壳圆周径向均匀分布。

图5 顶管掘进受力模型图Fig. 5 Force model of pipe jacking
Mindlin解计算简图如图6所示。由图可知,当弹性半空间体中某深度c处有沿z方向的竖向集中力pv时,土体中任意一点z方向的位移为w1; 有沿x方向的水平集中力ph时,土体中任意一点z方向的位移为w2。w1、w2可根据式(6)和式(7)求得。

图6 Mindlin解计算简图Fig. 6 Calculation diagram of Mindlin solution


(6)

(7)
(8)
(9)
式(6)—(9)中:x、y、z为计算点的坐标;c为集中力的作用点深度;ph为沿x方向的水平集中力;pv为沿z方向的竖向集中力。
2.2.1 开挖面附加推力
顶管在掘进过程中,在实际施加的支护压力与地层土水压力之间会存在压力差,即刀盘正面附加推力[11]。泥水平衡顶管掘进过程中,其泥水舱压力是均匀的,故开挖面附加推力也是均匀的。顶管机刀盘开挖面积分示意如图7所示。

图7 开挖面积分示意图Fig. 7 Sketch of excavation surface integration
开挖面圆形区域坐标转换为整体坐标,如下:
(10)
将式(10)代入式(7),得到开挖面附加推力微元引起的地表沉降
(11)
其中:
(12)
(13)
顶管正面附加推力引起的xyz坐标系中任意点的竖向位移
(14)
2.2.2 顶进摩擦力
1)顶管机头摩擦力引起的沉降示意如图8所示。规定顶管机外壳与土体产生的摩擦力在顶管机外壳表面积上均匀分布。

图8 机头摩擦力引起的沉降示意图Fig. 8 Sketch of settlement caused by friction of machine head
荷载微元局部坐标转换为整体坐标如下:
(15)
将式(15)代入式(7),得到顶管机外壳侧壁摩擦力微元引起的沉降如下:
(16)
其中:
(17)
(18)
顶管机外壳摩擦力引起xyz坐标系中的土体的位移
(19)
2)后续管节与土体摩擦力引起的地表沉降示意如图9所示。

图9 管节摩擦力引起的沉降示意图Fig. 9 Sketch of settlement caused by friction of pipe joints
后续顶管侧壁区域摩擦力微元局部坐标转换为整体坐标如下:
(20)
将式(20)代入式(7),得到后续管节摩擦力微元引起的沉降如下:


(21)
其中:
(22)

(23)
后续管节摩擦力引起xyz坐标系中的土体的位移
(24)
2.2.3 触变泥浆注浆压力
后续管节触变泥浆的同步注浆压力引起的地表沉降示意如图10所示。
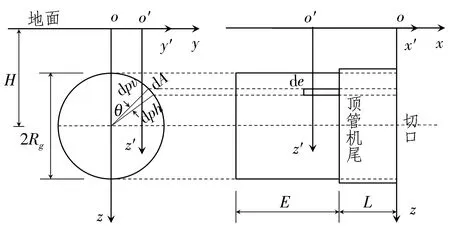
图10 同步注浆压力引起的沉降示意图Fig. 10 Sketch of settlement caused by simultaneous grouting pressure
由图10可知,注浆压力dp分解为水平分力dph=Rcosθdedθ和竖向分力dpv=Rsinθdedθ,本文仅考虑竖向分力dpv。E为后续管节总长度。
后续顶管侧壁区域注浆压力微元坐标转换后如下:
(25)
将式(25)代入式(6),得到触变泥浆注浆压力微元引起的沉降

(26)
其中:

(27)

(28)
同步注浆压力引起点(x,y,z)的竖向位移
(29)
2.3 总变形
将施工各因素引起土体中任意一点(x,y,z)的地面变形值进行叠加,即由式(2)、式(5)、式(14)、式(19)、式(24)、式(29)叠加,得到空间曲线顶管施工引起得地面竖向位移
w=wq+wf+wf1+wp+wloss+wover1+wover2。
(30)
以上各式的被积函数均不可积,采用MATLAB数学软件,对其采用自适应步长积分方法进行计算。其中,当水平和竖向无转弯时,即δh=0、δv=0时,式(30)退化为直线顶管掘进引起的地表沉降计算公式[12]。
3 工程算例对比分析
3.1 工程概况及参数取值
宁波市潘桥变电站迁建工程(隧道工程)采用泥水平衡顶管掘进施工,以2A工作井—1号工作井区间的S形空间曲线段施工为例进行计算,其轨迹为平曲线与竖曲线及竖向坡度叠合的S形空间曲线。工程平面如图11所示。实测断面为DC241-X,DC241为工程监测断面编号,X指断面上的测点号。以轴线为中心,两侧各分布4个测点,相邻间距分别为2、3、5、8 m。

图11 工程平面图Fig. 11 Plan of project
计算参数见表1,表中参数由现场监测及试验测量所得。
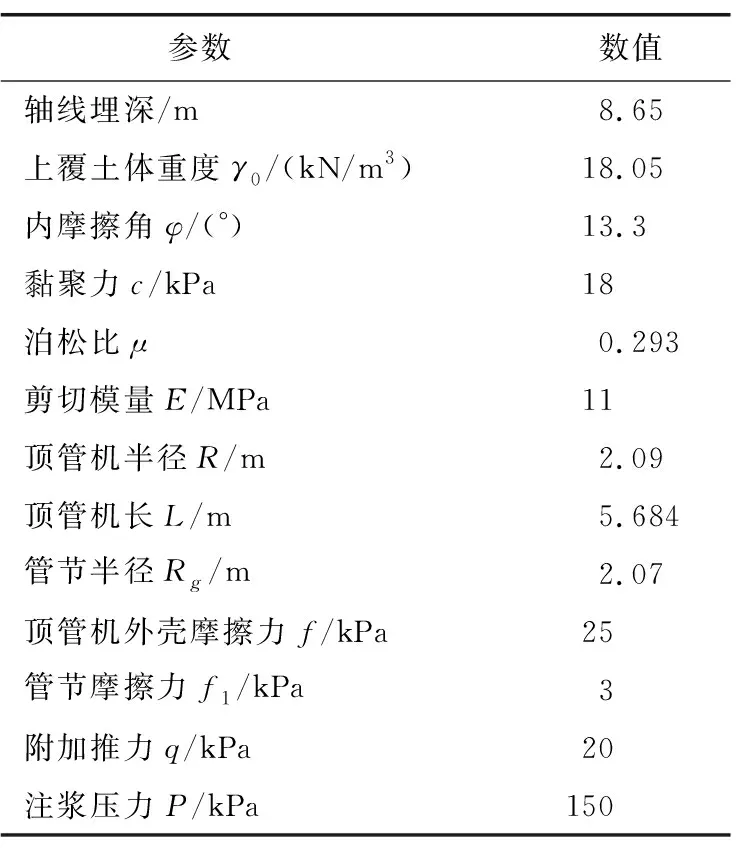
表1 计算参数Table 1 Calculation parameters
3.2 空间曲线顶管施工地表沉降计算
将表1参数代入式(30),通过计算得到S形空间曲线顶管施工引起的土体竖向位移曲线,如图12所示。由图可知,顶管施工各因素单独作用产生的沉降槽有明显区别,在顶管机曲线掘进的过程中,附加推力以及顶管机水平转弯超挖对沉降槽偏移有直接影响,其中水平转弯超挖引起的沉降量对沉降槽偏移起到关键作用。最终多因素叠加产生的沉降槽最大值偏移至顶进轴线的左侧,与实测数据规律一致。

图12 多因素引起的竖向位移曲线Fig. 12 Settlement curves caused by multiple factors
顶管机与土体摩擦力对土体扰动程度明显大于后续管节摩擦力,说明触变注浆润滑起到关键作用; 同时注浆填充会对地面有一定的抬升作用[13],隆起最大值约为3 mm; 顶管机尾部空隙是导致土体沉降的最大原因,占变形值的64%。由此可见,空间曲线顶管的沉降槽形态与直线段沉降槽形态有区别,其最大的差异是曲线顶管掘进产生的沉降槽发生了偏移。理论计算的沉降槽与实测沉降槽形态较为接近,最大值误差约为2%,验证了理论模型对沉降预测的有效性。
顶管机转弯挤土超挖示意如图13所示。由图可知,顶管右转时,通过控制顶管机机头纠偏油缸左侧行程大于右侧行程,实现顶管机机头向右偏转,此时顶管机对曲线内侧(顶进轨迹右侧)的土体产生挤压,在顶管机发生偏转的同时,顶管机左侧与土体的接触位置产生了间隙。曲线内侧管土接触相对紧密,土体损失较小,地表沉降发展较小;右侧管土间隙被顶管机尾阻隔,导致触变注浆不能及时将曲线外侧的间隙填充,在此期间,周围土体卸荷,向空隙运动,使得土体扰动更为严重,地表沉降较大[14]。

图13 顶管机转弯挤土超挖示意图Fig. 13 Sketch of soil squeezing and overbreak of pipe jacking machine
4 S形空间曲线参数对地表沉降的影响及控制措施
由理论模型计算与实例对比可知,空间曲线顶管施工的地表沉降槽偏移是由曲线超挖造成的,因此,通过使用本文计算模型对曲线半径的因素进行影响分析,并通过优化注浆工艺对地表沉降进行控制。
4.1 曲线半径
4.1.1 平曲线半径影响
为研究不同平曲线半径对土体位移的影响规律,保持竖曲线半径Rv=3 000 m,分别对平曲线Rh1=200 m、Rh2=300 m、Rh3=400 m、Rh4=600 m、Rh5=700 m 5种不同半径进行计算。
不同半径平曲线施工的沉降槽曲线如图14所示。由图可知,地表沉降最大值与曲线半径呈负相关,Rh1~Rh5对应的最大沉降值依次为34.19、28.19、24.19、20.19、19.19 mm。且最大值点都出现在弯道外侧。当平曲线半径R≤300 m时,沉降最大值接近或大于警戒值30 mm。故管节外径4.14 m、管节长度1.5 m的顶管在曲线段进行弯道设计时,经过对沉降值的分析,得到平曲线转弯半径应尽量不小于300 m。

图14 不同半径平曲线施工的沉降槽曲线图Fig. 14 Settlement trough curves with different radius of horizontal curve
沉降槽偏移量与平曲线半径的关系如图15所示。由图可知,最大沉降值随平曲线半径的增大而减小,两者之间近似呈线性关系。究其原因,随顶管曲线半径的增大,顶管机转弯纠偏需要超挖的土体体积减小,向超挖空隙运动的土体量减少,使得曲线外侧的最大值偏移量随之减小。
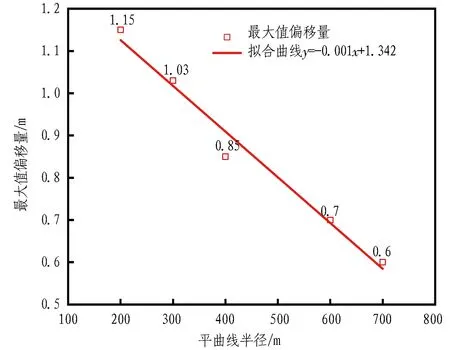
图15 沉降槽偏移量与平曲线半径的关系Fig. 15 Relationship between deviation of settlement trough and radius of horizontal curve
4.1.2 竖曲线半径影响
为研究不同竖曲线半径对土体位移的影响规律,保持平曲线半径Rh=500 m,分别对竖曲线Rv1=2 000 m、Rv2=2 500 m、Rv3=3 500 m、Rv4=4 000 m 4种不同曲线半径进行计算。
不同半径竖曲线超挖的沉降槽曲线如图16所示。由图可知,竖向转弯产生的沉降槽是以顶管轴线中心对称的,与其他施工因素产生的沉降曲线叠加之后,不会影响沉降槽的偏移。

图16 不同半径竖曲线超挖的沉降槽曲线图Fig. 16 Settlement trough curves over excavated by vertical curves of different radii
4.2 空间曲线形态
由理论计算结果和实测数据规律总结可知,顶管转弯对沉降槽形态影响较大,分别对4种转弯方式进行计算,即在顶管顶进方向上进行右上转弯、右下转弯、左上转弯和左下转弯。顶管机4种转弯超挖示意如图17所示。

(a) 向右下转弯(b) 向右上转弯

(c) 向左下转弯(d) 向左上转弯图17 顶管机4种转弯超挖示意图Fig. 17 Sketch of two types of overbreak when pipe jacking machine turns left
在理论计算空隙量的过程中,将其简化为不同水平和竖向转弯单独产生的接触空隙相叠加。通过地层扰动计算模型计算的4种顶进转弯方式所产生的沉降槽曲线如图18所示。

图18 4种不同转弯产生的沉降槽曲线Fig. 18 Settlement trough curves generated by four different turns
图18中计算规定: 水平转弯半径Rh=500 m,竖向转弯半径Rv=3 000 m。由图18可知,顶管机沿空间曲线轨迹顶进,在无超挖刀参与掘进的过程中,顶管机转弯引起地面产生的沉降槽的最大值会发生偏移,最大值的偏移方向与顶管机水平转弯方向相反,偏向弯道外侧。且顶管机竖向转弯超挖不会影响沉降槽最大值的偏移。
4.3 沉降控制措施
由3.2节可知,顶管施工地层损失引起的土体扰动占比最大,故在顶进过程中,同步注入触变泥浆工艺的优化,是减少顶进阻力、控制沉降的重要一环。
以本工程1号井—2A号井线路的空间曲线顶管为例,通过对空间曲线顶管施工产生的空隙体积计算(单节管节长度),进行注浆量的合理分配。其中,理论注浆量=理论地层空隙体积,R为顶管机刀盘半径,Rg为后续管节半径,l为隧道每节管节长度,δ为平曲线纠偏最大接触空隙量,计算得到δ=0.008 m。竖曲线产生的特殊超挖间隙忽略不计。
单管节长度范围顶管机尾部环形间隙体积
v0=(R2-Rg2)πl。
(31)
顶管机转弯外侧接触空隙体积
(32)
空间曲线段单管节长度的总空隙体积
(33)
单节顶管的长度l为1.5 m,通过计算得顶管机外径为4.18 m,后续管节外径为4.14 m,在平曲线半径为500 m的曲线段顶进过程中,每节管节长度与土体的接触体积为0.46 m3,即理论注浆量。顶管施工中,实际注浆量与理论注浆量之比定义为充盈系数。实际施工中单节注浆量大于1.4 m3时,对地层变形的抑制效果明显; 当注浆量大于2 m3时,地面冒浆,说明土层中已经充斥过量浆液。在宁波地区,穿越土质以淤泥质黏土为主,故埋深8~11 m的平曲线半径500 m的曲线顶管施工过程中,触变泥浆的充盈系数宜为3~4。
在曲线段掘进过程中,管节吊装,注浆管安装好之后,通过控制注浆时间和压力,进行全周注浆;并对顶管机转弯的超挖侧的空隙进行加量注浆,及时填补超挖空隙,减小地表沉降的发展。
5 结论与建议
本文以宁波市潘桥变电站顶管隧道工程为背景,构建了S形空间曲线顶管地层扰动计算模型,计算了曲线顶管施工过程中各项顶进参数及地层损失共同作用下的地表竖向位移,并与实测数据进行对比,验证了计算模型的可靠性。主要结果如下:
1)构建了符合实际工况的S形空间曲线段顶管施工引起地层扰动的计算方法,理论计算值与实测值吻合较好,能够对地表沉降进行预测。
2)顶管沿S形空间曲线顶进施工时,顶管机对弯道内侧的土体产生挤压,同时与弯道外侧土体产生了超挖间隙,使得弯道外侧土体损失大于弯道内侧,沉降槽最大值偏移至弯道外侧、不在顶管机轴线正上方。因此,地表监测点应布置在弯道外侧偏离轴线1.0 m处。
3)曲线顶管施工产生的地表沉降槽最大值偏移只与顶管的水平转弯有关,水平转弯造成的超挖对偏移量影响最大。顶管水平转弯半径越大,沉降槽最大值的偏移量越小。
4)地层损失是造成地表沉降的主要原因。因此,在S形空间曲线顶进时,理论注浆量应包括环形空隙与超挖间隙注浆量体积之和,在类似地层条件下曲线顶管工程中,充盈系数宜为3~4。
通过对本工程的理论计算与实际监测的对比,可以对曲线隧道施工的土体变形监测方案设计提供参考。但是在实际工程中,影响沉降最大值偏移量的因素较多,按具体参数计算,偏移预测结果会更为准确。

