挤压性大变形隧道分层初期支护适应性分析

刘志强， 朱建林， 吴 剑， 匡 亮， 唐思聪

(1. 中铁西南科学研究院有限公司， 四川 成都 611731； 2. 西南交通大学 交通隧道工程教育部重点实验室， 四川 成都 610031； 3. 中铁二院工程集团有限责任公司， 四川 成都 610031)

0 引言

目前，高地应力作用下挤压性围岩大变形问题突出，支护与围岩变形难以协调，支护结构易变形侵限、混凝土开裂、钢架扭曲等，严重影响工程质量与进度[1-3]。在结构分析中，充分考虑围岩的流变特性，可使支护参数和支护时机的选取更为合理[4-6]。为有效控制围岩大变形，选用分层支护结构不失为一种有效的手段，且在国内许多工程中得到成功应用[7-13]。尤显明等[7]以兰渝铁路木寨岭隧道岭脊核心段施工为例，给出“超前导洞应力释放+圆形4层支护结构+径向注浆+长锚杆+长锚索”的综合变形控制方案；喻有彪[8]以景寨隧道为例，在克服高地应力大变形实践过程中，摸索出以多层初期支护为主要措施的综合方案，在变形控制、进度指标提升、经济性提升等方面均取得了较好效果；司剑钧[9]针对兰渝铁路两水隧道极高地应力软岩大变形问题，开展双层初期支护和双层衬砌试验，为隧道支护和衬砌结构优化提供了实践依据；王洪昌[10]研究了双层初期支护在牡绥线扩能改造工程兴源隧道围岩大变形中的应用效果；李华伟[11]采取双层初期支护技术，有效地控制了黑龙江省某隧道的异常变形。

采用分层支护时，支护时机的选取尤为重要。钟友江等[14]结合成兰铁路云屯堡隧道，认为第2层初期支护应在第1层初期支护结构不被破坏前及时施作；唐雄俊[15]引入初期支护屈服轴力与围岩变形折减率作为合理支护时机的判据，以此来确定深埋隧道合理支护时机；方中明等[16]以湖北省宜巴高速公路峡口隧道为例，分析了隧道水平收敛和拱顶下沉分别在隧道开挖后12 d和15 d变形量达到其总变形量的90%，认为合理的支护时机应在隧道开挖后15～25 d；周勇等[17]针对广梧高速公路牛车顶隧道，探讨了岩体流变情况下隧道二次衬砌支护时机确定的理论计算方法。

综上所述，目前对于挤压性大变形隧道的支护，给出了分层支护的解决思路，但支护参数的选取对工程经验颇为依赖，而针对分层支护参数和支护时机的系统性研究较少，且研究成果缺乏普适性。因此，本文基于挤压性大变形隧道的流变特性，采用数值模拟方法分析不同变形等级下初期支护分层支护模式的合理性，以及支护时机的适应性，以期为类似工程提供参考。

1 假定条件

为探讨挤压性大变形隧道采用分层初期支护的技术路径，简化部分条件做如下假定。

1)同一围岩参数在不同埋深下所表现出来的变形等级可能存在差异，因此，基于兰渝铁路木寨岭隧道现场大型剪切试验及其流变反分析确定围岩计算参数，并通过改变埋深后的整体变形量值对应不同变形等级。

2)鉴于目前初期支护中钢架与喷射混凝土联合作用的机制研究并未明确，因此，仍采用刚度等效原则将钢架弹性模量折算到混凝土弹性模量中。

3)未考虑开挖工法，简化为全断面开挖，喷射混凝土及锚杆(索)锚固施工后未考虑待强时间，认为施作后即发挥作用。

4)仅讨论初期支护的分层支护参数及施作时机，二次衬砌的施作时机可参考兰渝线、成兰线经验，并在变形未侵限的条件下延后施作。

2 等效支护抗力量化分析

2.1 量化分析方法

初期支护中喷射混凝土(含钢架)作为与隧道围岩直接接触的结构，通过与围岩的协同变形来维持围岩的稳定性，可采用荷载结构法将围岩荷载作为外荷载作用在初期支护结构上，通过结构自身受力状态判断结构稳定性及极限状态。

初期支护中的锚杆(索)深入围岩内部，通过相对位移及注浆加固抑制围岩变形，可通过位移等效原则分析其所能提供的等效支护抗力。位移等效原则指的是隧道全断面开挖并同时施作锚杆(索)变形稳定后会产生一个位移u1，相同条件下，在隧道开挖后洞壁处施作大小为p的径向支护力，围岩变形稳定后产生位移u2，若u1≈u2，则可认为锚杆(索)形成的群锚效应的等效支护抗力为p。

因此，基于荷载结构法和位移等效原则可量化分析不同初期支护参数能够提供的等效支护抗力。

2.2 喷射混凝土等效支护抗力分析

运用有限元分析软件，通过荷载结构法分析不同厚度C25和C30喷射混凝土与不同型号钢拱架组合的初期支护达到其承载极限时所能提供的最大支护抗力。喷射混凝土力学参数如表1所示。另取围岩弹性反力系数为150 MPa/m，泊松比ν为0.4。

表1 喷射混凝土力学参数Table 1 Mechanical parameters of shotcrete

计算以单线隧道为例，隧道宽10.48 m、高11.98 m。根据规范，竖向荷载为q，水平荷载为e=λ·q。根据荷载图示(见图1(a))，建立计算模型如图1(b)所示。其中，支护结构用Beam3单元模拟，地层支护用Link10单元模拟，且只受压。

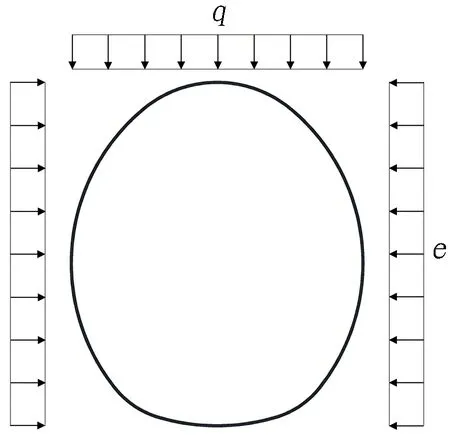
(a) 支护结构荷载示意图

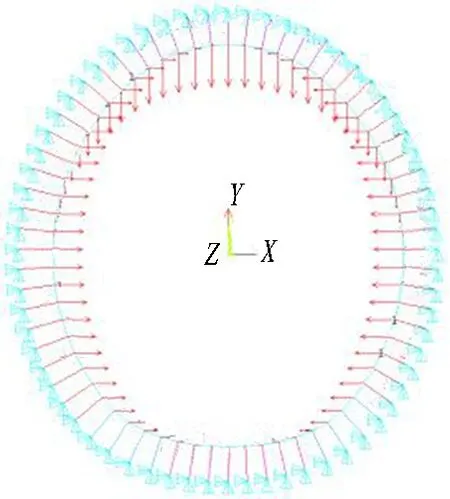
(b) 计算模型图1 支护结构荷载图示和计算模型Fig. 1 Loading diagram and calculation model of supporting structure

根据试算，支护结构为抗压强度控制，故施加不同的荷载作用，将支护结构达到抗压强度设计值时的荷载大小作为其在现行规范要求下的支护抗力值。经计算，得到不同初期支护下的等效支护抗力，如表2和表3及图2和图3所示。

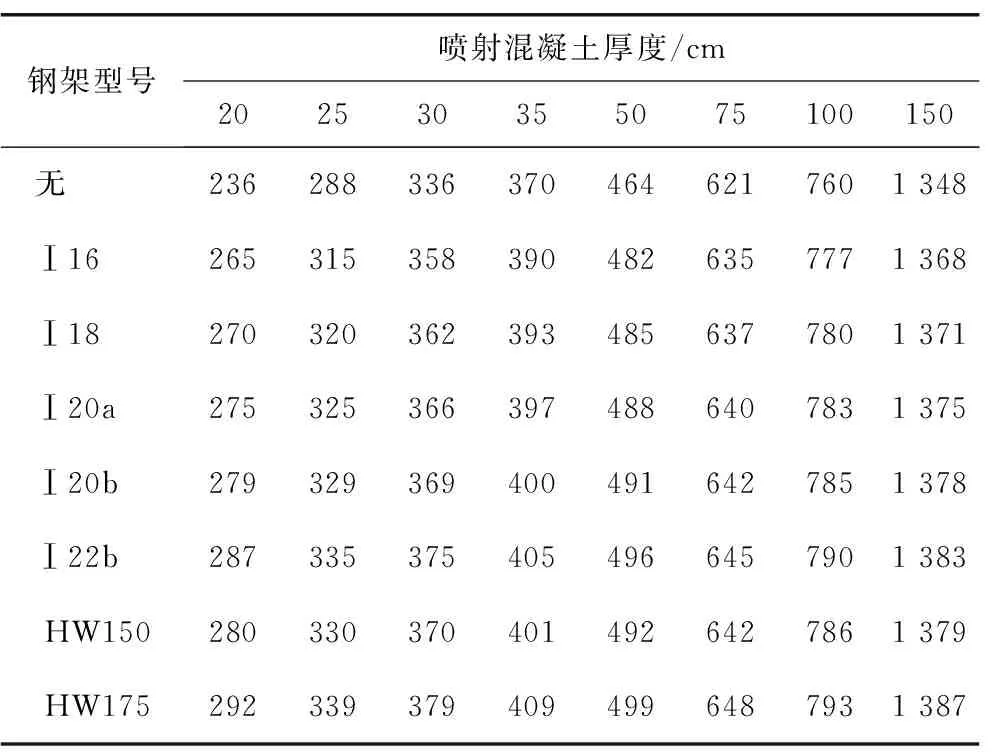
表2 C25喷射混凝土+钢架等效支护抗力Table 2 C25 shotcrete and steel frame equivalent resistance kPa

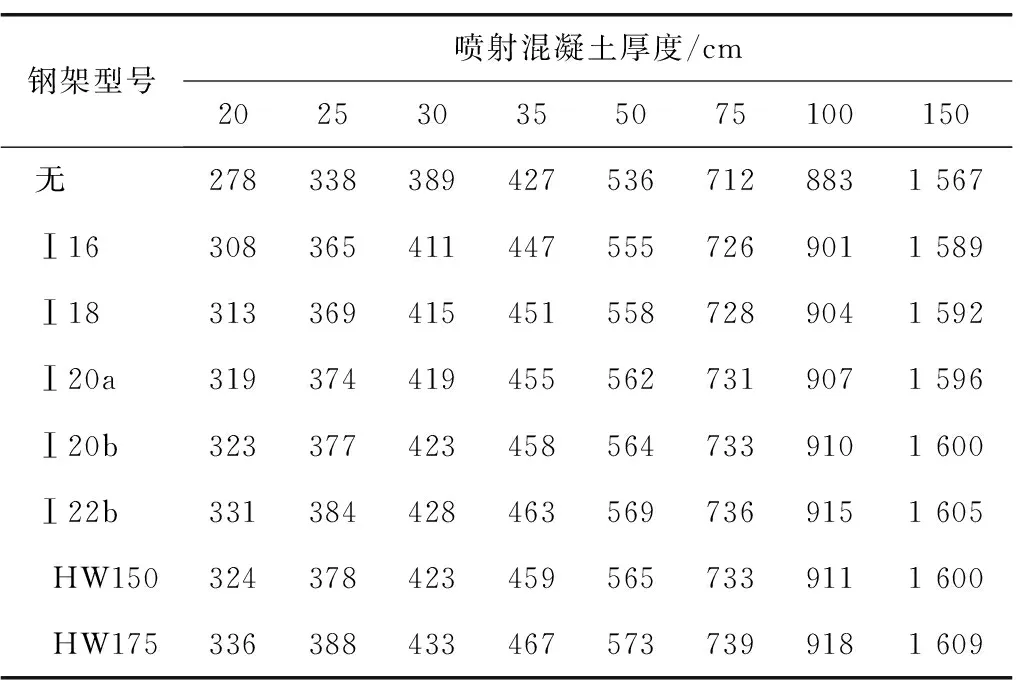
表3 C30喷射混凝土+钢架等效支护抗力Table 3 C30 shotcrete and steel frame equivalent resistance kPa

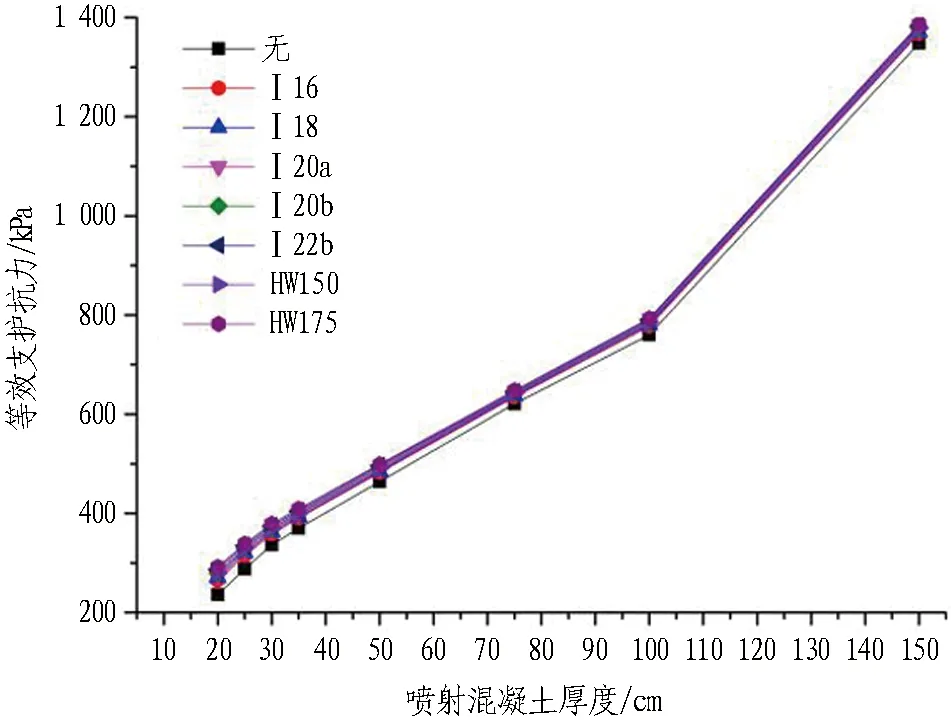
图2 C25喷射混凝土+钢架等效支护抗力曲线Fig. 2 Curves of C25 shotcrete and steel frame equivalent resistance

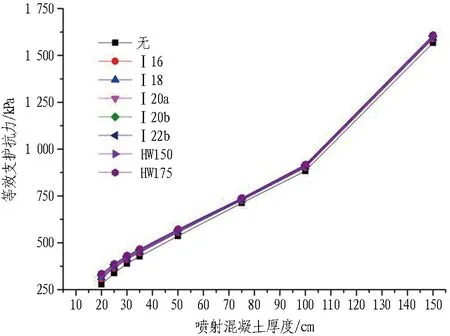
图3 C30喷射混凝土+钢架等效支护抗力曲线Fig. 3 Curves of C30 shotcrete and steel frame equivalent resistance

可知，随着同一等级喷射混凝土厚度的增加，其所能提供的支护抗力不断增大，采用刚度等效原则计算时，钢架的施作对喷射混凝土的支护能力起到了一定的增强作用，但增强效果不是特别明显，在通常设计厚度下(25～35 cm)增加10%～18%；同一等级喷射混凝土厚度情况下，C30喷射混凝土的等效支护抗力较C25喷射混凝土增加16%～18%。

2.3 锚杆(索)等效支护抗力

2.3.1 模型及参数

采用位移等效原则，通过数值计算分析砂浆锚杆和预应力长锚索的等效支护抗力。采用地层结构模型，埋深取300 m，隧道断面如图1(a)所示。计算模型为二维平面应变模型。

现场监测位移数据变化规律显示围岩具有明显的时效流变特性，选用广义Kelvin黏弹塑性流变模型作为围岩本构模型(见图4)。结合位移监测数据，通过最小二乘法曲线拟合得到围岩本构参数，如表4所示。

表4 黏弹塑性围岩本构参数Table 4 Viscoelastic-plastic surrounding rock parameters

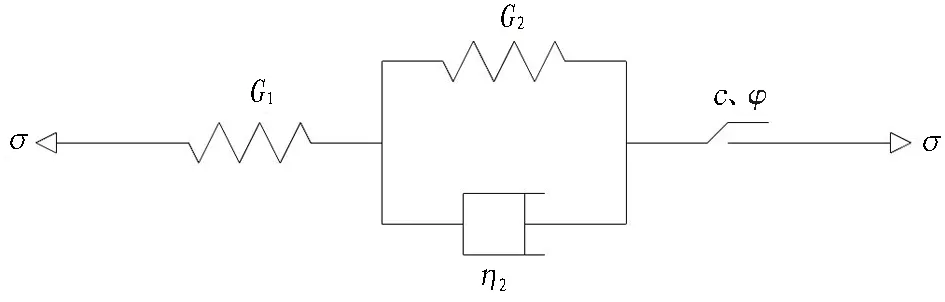
σ为围岩应力; G1、G2为剪切模量； η2为黏弹性系数； c为黏聚力; φ为摩擦角。图4 广义Kelvin黏弹塑性流变模型Fig. 4 Generalized Kelvin viscoelastic-plastic rheological model

锚杆(索)均采用cable单元进行模拟，并根据各部位的不同功能分别赋予不同的材料参数。砂浆锚杆参数如表5所示。预应力锚索参数如表6所示。

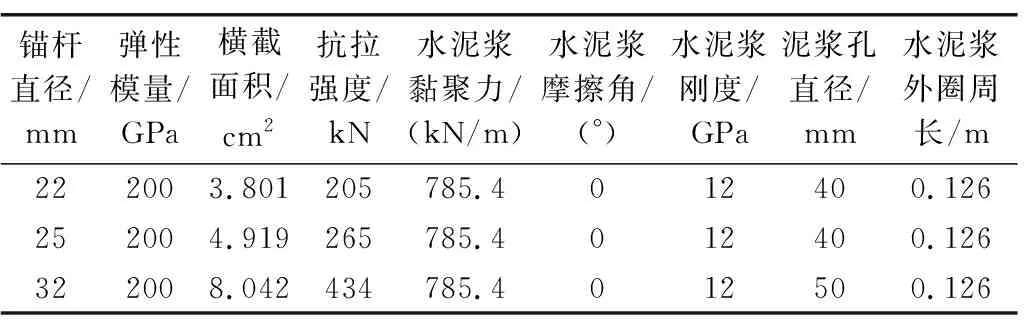
表5 砂浆锚杆参数Table 5 Mortar bolt parameters

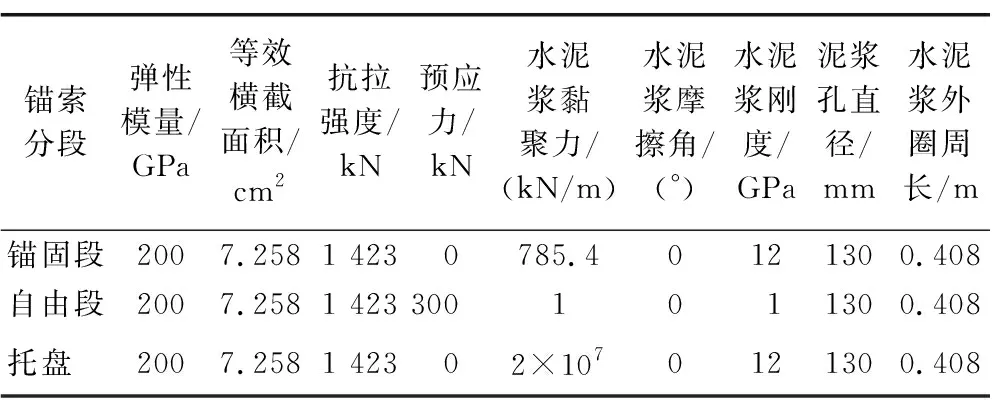
表6 预应力锚索参数Table 6 Pre-stressed cable parameters

砂浆锚杆沿隧道断面全环设置，间距为1.0 m×1.0 m(环×纵)。锚索由4根φ15.2 mm的钢绞线相互绞合而成，分为托盘、自由段和锚固段3部分。其中，自由段占锚索长度的2/3，锚固段占锚索长度的1/3。锚索自由段施加300 kN的预应力，隧道左右边墙分别设置5根锚索，间距为2.0 m×1.0 m(环×纵)。锚杆、锚索设置示意如图5所示。

图5 锚杆、锚索设置示意图Fig. 5 Bolt and cable setting diagram

2.3.2 围岩特征曲线

计算得到裸洞围岩变形稳定后边墙单侧收敛位移与径向支护抗力间的关系，如图6所示。

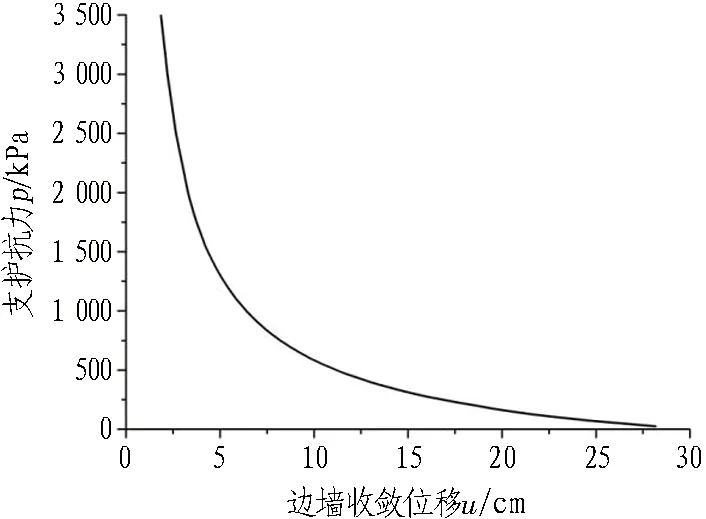
图6 围岩位移与支护抗力关系曲线Fig. 6 Curve of relationship between surrounding rock displacement and support resistance

在隧道开挖的同时施作锚杆(索)，待围岩变形稳定后得到围岩边墙收敛位移u2。将u2与图6进行对比分析，则u2位移量值对应的支护抗力就是施作锚杆(索)的等效支护抗力。

2.3.3 等效支护抗力

计算得到不同直径、不同长度砂浆锚杆的等效支护抗力如表7和图7所示。同一直径的锚杆，其所能提供的支护抗力随锚杆长度的增加而逐渐增大。当锚杆长度从4 m增加到8 m时，锚杆提供的支护抗力增量较大；而当锚杆长度从8 m增加到12 m时，锚杆提供的支护抗力增量较小。这说明一味地增加锚杆的长度并不能使锚杆的支护效果明显增加；同一长度的锚杆，随着锚杆直径的增大，其所能提供的支护抗力逐渐增大，且锚杆直径的增大对锚杆支护效果具有明显的提高作用。

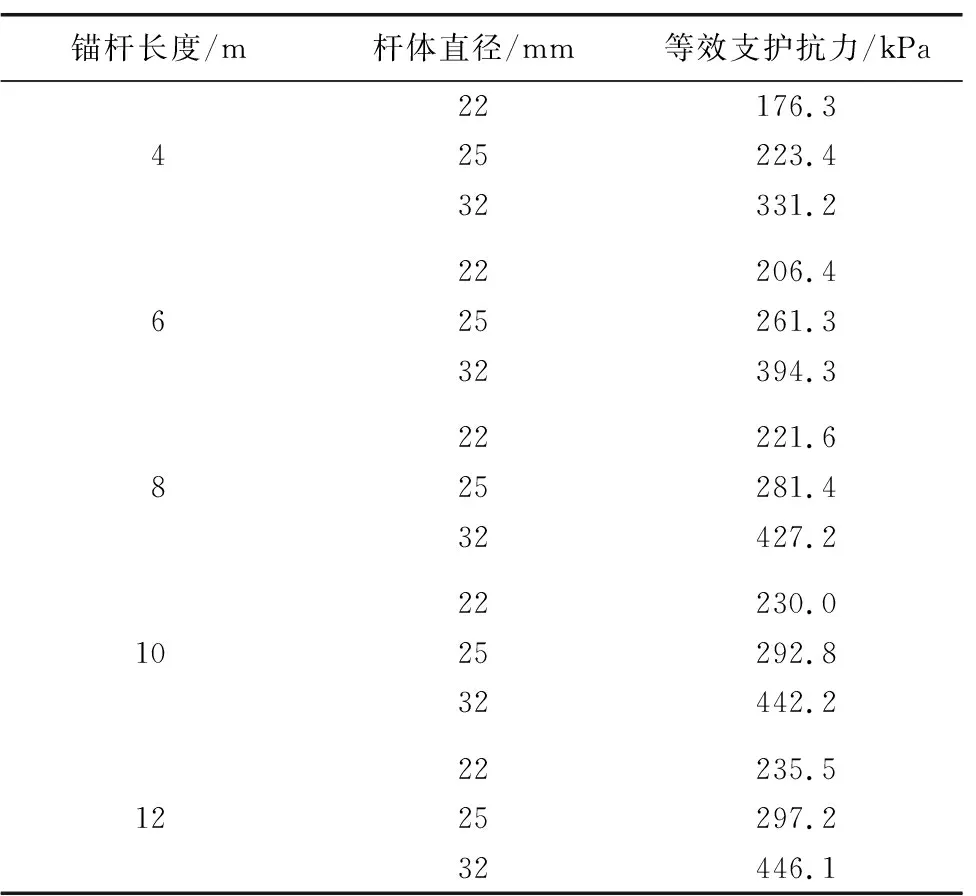
表7 砂浆锚杆等效支护抗力Table 7 Mortar bolt equivalent resistance

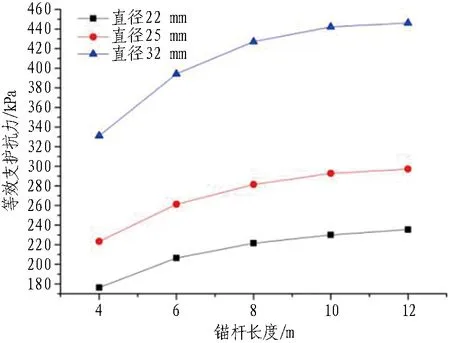
图7 砂浆锚杆等效支护抗力曲线Fig. 7 Curves of mortar bolt equivalent resistance

不同长度预应力锚索的等效支护抗力如表8和图8所示。在该计算工况下，锚索长度小于12 m时，随着锚索长度的增加，等效支护抗力不断增大；当锚索长度等于12 m时，等效支护抗力达到最大；而当锚索长度大于12 m时，随着锚索长度的增加，其对应的等效支护抗力不断减小。

表8 长锚索等效支护抗力Table 8 Long anchor cable equivalent resistance

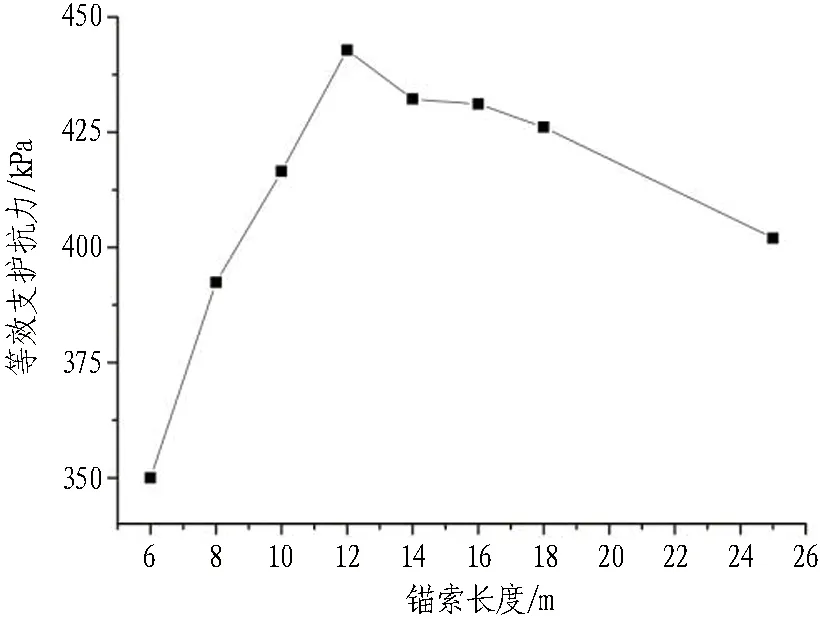
图8 长锚索等效支护抗力曲线Fig. 8 Curve of long anchor cable equivalent resistance

预应力长锚索的等效支护抗力会出现随锚索长度增加先增大后减小的规律，这主要与锚索是否达到最大轴力值相关。通过分析锚索长度与围岩塑性区范围之间的关系，发现在一定长度锚索范围内，随着锚索长度的增加，锚索对围岩变形的控制范围增大，使得锚索长度越长，其等效支护抗力越大；当锚索长度增加并延伸出围岩塑性区范围，锚索在围岩变形过程中轴力未达到最大值，其相对应的等效支护抗力反而减小。

图9示出300 m和600 m埋深下18 m长锚索轴力与围岩塑性区对应图。由图可知： 300 m埋深时，锚索超出了围岩塑性区，最大轴力为1 255 kN，未达到锚索抗拉极限1 423 kN，说明锚索的约束能力没有完全发挥；600 m埋深时，锚索在围岩塑性区范围内，其轴力达到抗拉极限1 423 kN，锚索的约束能力得到完全发挥。

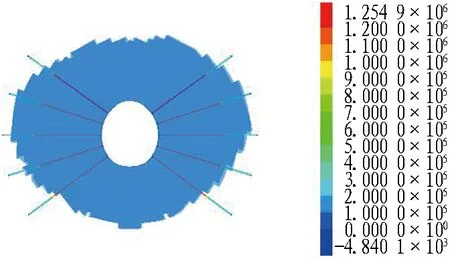
(a) 300 m埋深

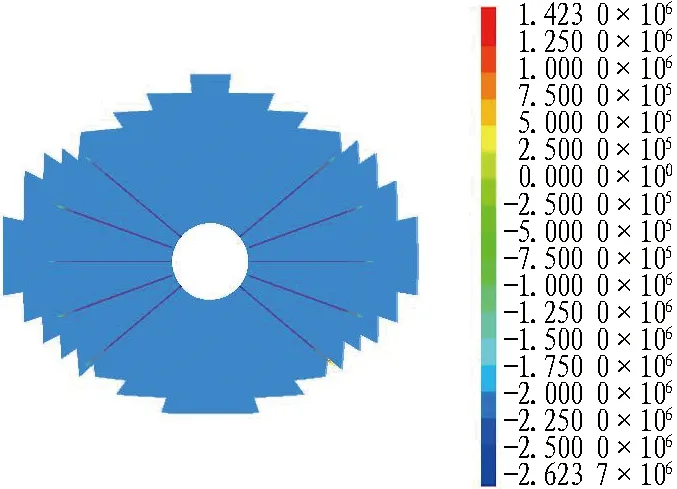
(b) 600 m埋深轴力的单位为N。图9 18 m长锚索轴力与围岩塑性区对应图Fig. 9 18 m long anchor cable axial force corresponding to surrounding rock plastic zone

针对不同的工程地质条件，还需要对锚杆、锚索的支护抗力进行进一步计算，得到准确的等效支护抗力值。

3 喷射混凝土弹塑性参数反演

在分析中，若将喷射混凝土考虑为线弹性，通常在变形很小的时候，喷层结构受力就超过其承载极限，但实际工程中，喷射混凝土破坏时的变形值远大于弹性变形理论值。为反映初期支护能随围岩变形产生较大的位移，选用基于摩尔-库仑屈服准则的弹塑性模型，并通过支护抗力等效原则确定相关力学参数。

以25 cm厚C25喷射混凝土+HW150钢架为组合的支护结构为例，通过荷载结构法可知其等效支护抗力约为330 kPa。根据图6可知，隧道开挖后在330 kPa抗力的支护下围岩边墙单侧收敛约为14.56 cm。保持支护结构的弹性模量和泊松比不变，通过资料调研，在一定范围内调整其黏聚力c和摩擦角φ，使得隧道施作支护结构产生的围岩边墙单边收敛与330 kPa支护抗力产生的变形规律一致，如图10所示，从而确定支护结构的黏聚力c和摩擦角φ。

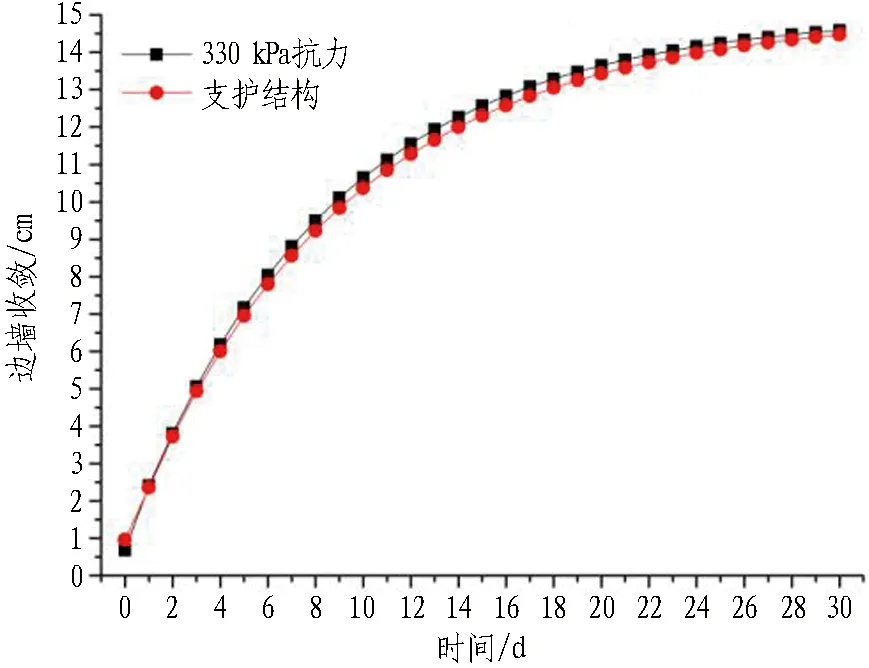
图10 不同支护围岩边墙单侧收敛Fig. 10 Unilateral convergence of sidewalls of surrounding rocks with different supports

据此方法计算，得到常用的8种初期支护的弹塑性参数，如表9所示。

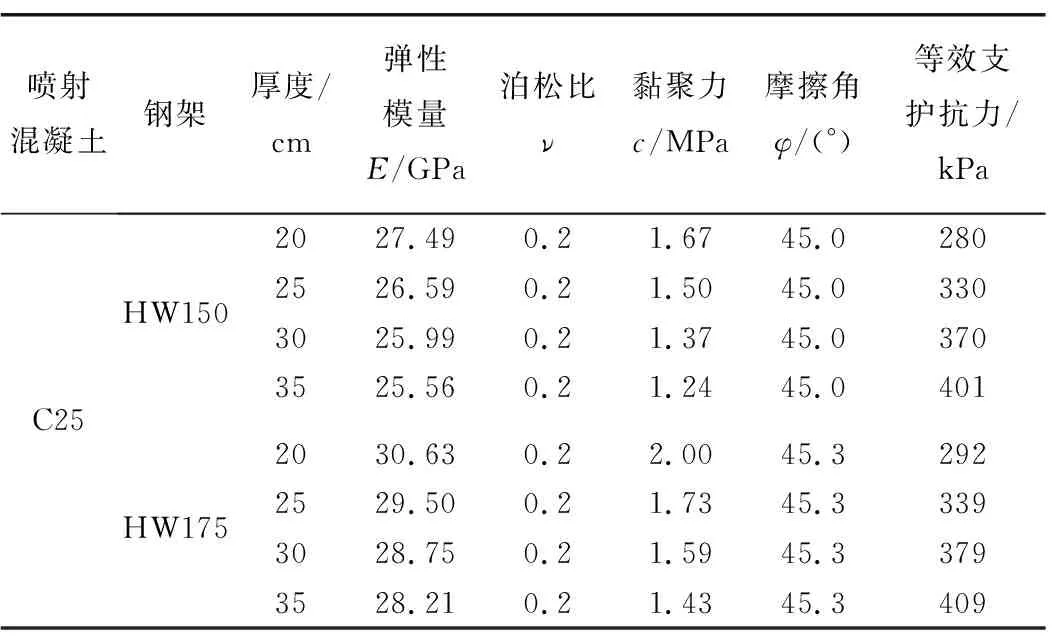
表9 初期支护的弹塑性参数反演结果Table 9 Elastic-plastic parameters inversion results of primary support

4 分层初期支护适应性分析

4.1 分层支护的思路

4.1.1 围岩与支护相互作用曲线

考虑流变效应的围岩与支护相互作用曲线如图11所示。

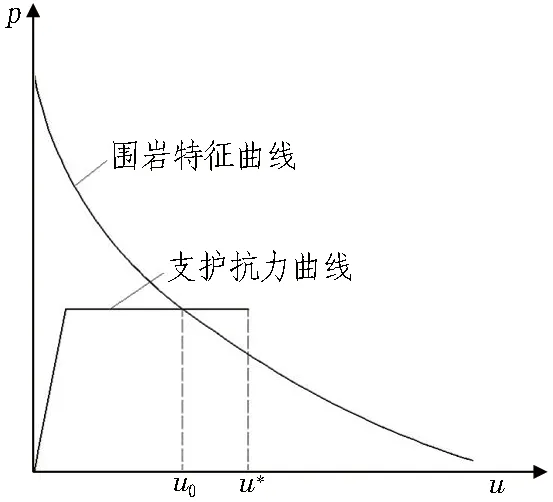
u0表示围岩特征曲线与支护曲线交点的位移值；u*表示结构破坏时现场的位移监测值。图11 围岩与支护相互作用曲线Fig. 11 Interaction curve between surrounding rock and support

u0和u*存在3种关系： 1)当u0u*时，表明支护参数不能抵抗住围岩压力，需在变形值达到u*之前施作下一层支护。以此类推，利用分层支护使最终的支护参数条件下u0≤nu*(n表示总计n层支护)。这是分层支护参数和时机的确定思路。

从变形能量的角度，隧道开挖后因临空面的存在，洞周围岩向洞内积聚，一定的支护条件所能抑制围岩积聚产生的变形能量是有限的，当每一层支护能够维持的围岩变形能量超过其阈值后，支护与围岩之间的平衡会被打破，围岩会因进一步积聚能量产生持续的变形，因此需要施作下一层支护，直至分层支护所能提供的稳定能力超过围岩总的变形能量时，两者达到平衡状态。

在分析过程中，需要明确以下3点： 1)确定支护结构的极限抗力； 2)构建如图11所示的支护抗力曲线； 3)确定u*的取值。

对于u*，国内大量现场案例均表明，当u*=15～30 cm时[18]，喷射混凝土出现开裂现象，故u*可取为15 cm(隧道单侧边墙位移值)。考虑支护参数时，初步按以往支护经验进行验算。

计算模型采用地层结构二维平面应变模型，计算过程中的时间等同于现实中的真实时间。通过对不同变形等级下挤压性大变形隧道的支护参数进行分析，提出不同变形等级下分层支护的参数建议及合理支护时机。

4.1.2 计算模型

数值计算模型尺寸(X×Y×Z)为200 m×1 m×200 m，计算参数同上文，顶部施加荷载边界实现对不同埋深的模拟。局部计算模型如图12所示。

图12 计算模型Fig. 12 Calculation model

计算隧道裸洞在埋深为300、450、600 m时，水平收敛位移值(两侧之和)分别为29.4、64.6、95.5 cm，分别对应轻微、中等和强烈大变形3个等级[19]。

4.2 轻微大变形与1层支护

轻微大变形地段采用1层支护，开挖后即施作喷射混凝土+型钢支护，及时施作锚杆。经计算，25 cm厚C25喷射混凝土+HW150@1.0 m的等效支护抗力为330 kPa，3.5 m长φ25砂浆锚杆@1.0 m×0.6 m(环×纵)的等效支护抗力为273.3 kPa。1层支护作用下围岩与支护变形时程曲线如图13所示。轻微大变形地段围岩与支护相互作用曲线如图14所示。

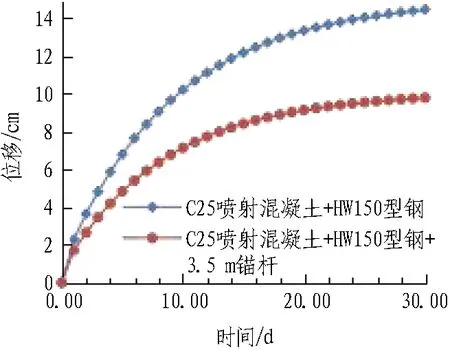
图13 1层支护作用下围岩与支护变形时程曲线Fig. 13 Surrounding rock and support deformation curves under one-layer support

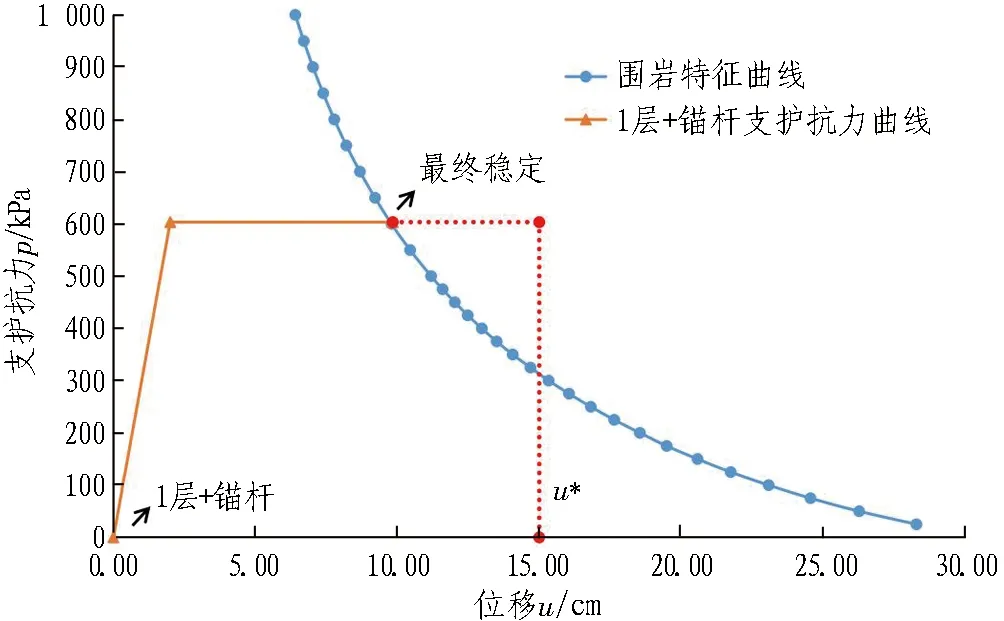
图14 轻微大变形地段围岩与支护相互作用曲线Fig. 14 Interaction curve between surrounding rock and support for slightly-large deformation

由图13和图14可知： 仅采用C25喷射混凝土+HW150型钢支护时，围岩与结构最终变形在14.53 cm左右，接近u*=15 cm；及时施加3.5 m长锚杆后，变形最终控制在9.84 cm，小于u*，表明支护形式合理。故轻微大变形地段建议采用单层初期支护+短锚杆的支护形式，即： 25 cm厚C25喷射混凝土+HW150@1.0 m，及时施作3.5 m长φ25砂浆锚杆@1 m×0.6 m(环×纵)。

4.3 中等大变形与2层支护

2层及以上支护尚需考虑支护时机，拟采用2层支护进行中等大变形地段围岩变形控制。围岩的支护特征曲线如图15所示。

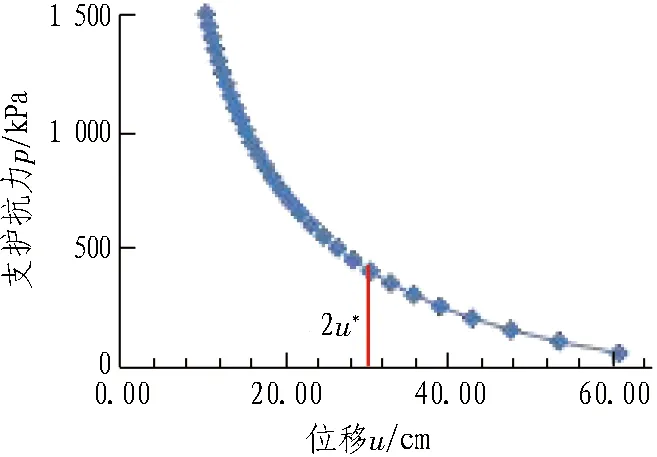
图15 中等大变形地段围岩与支护相互作用曲线Fig. 15 Surrounding rock and support curve of moderately-large deformation

4.3.1 支护参数选取

2层支护作用下，总体变形不应大于2u*，即30 cm，此时对应的支护抗力为400～450 kPa。在实际工程中，考虑一定的安全富余，单次变形宜控制在10 cm，最终所需支护抗力约为700 kPa。故1层支护选用25 cm厚C25喷射混凝土+HW150@1.0 m和6 m长φ25砂浆锚杆@1.0 m×0.6 m(环×纵)，等效支护抗力分别为330 kPa和339.6 kPa；2层支护选用25 cm厚C25喷射混凝土+HW150@1.0 m，等效支护抗力为330 kPa。总支护抗力为999.6 kPa。

4.3.2 2层支护时机选取

1层支护施加后的围岩与结构变形时程曲线如图16所示。

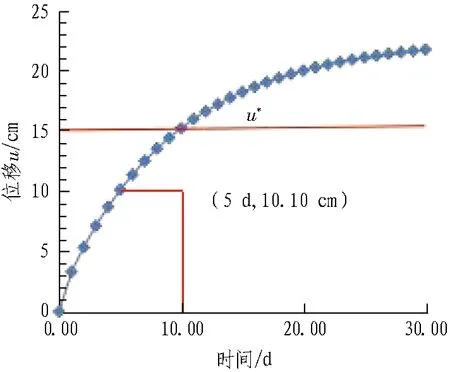
图16 1层支护作用下围岩与结构变形时程曲线Fig. 16 Surrounding rock and support deformation curve under one-layer support

由图16可知，1层支护的最终稳定值为21.72 mm，大于u*，承载能力不满足要求。宜在初期支护施加5 d后施作2层支护，此时围岩实际位移值为10.10 cm。2层支护施加后的围岩与结构变形时程曲线如图17所示。

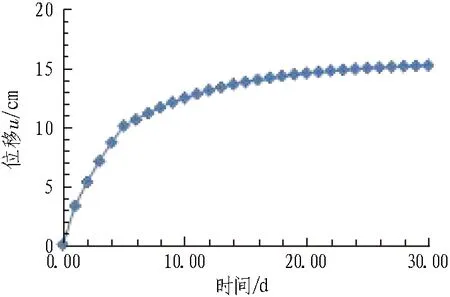
图17 2层支护作用下围岩与结构变形时程曲线Fig. 17 Surrounding rock and support deformation curve under two-layer support

由图17可知，2层支护施加后，最终的变形值为15.25 mm，小于2u*，支护参数合理，该过程的围岩与支护相互作用曲线如图18所示。故中等大变形地段建议采用2层初期支护+短锚杆的支护形式，即： 1层支护25 cm厚C25喷射混凝土+HW150@1.0 m和6 m长φ25砂浆锚杆@1 m×0.6 m(环×纵)，开挖后即施作； 2层支护25 cm厚C25喷射混凝土+HW150@1.0 m，开挖5 d后施作。

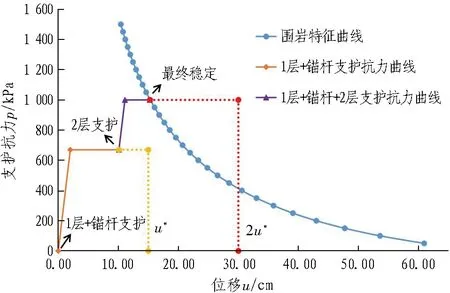
图18 中等大变形地段围岩与支护相互作用曲线Fig. 18 Interaction curve between surrounding rock and support for moderately-large deformation

4.4 强烈大变形与3层支护

不同于轻微和中等大变形，强烈大变形地段的隧道轮廓需优化，通常采用圆形洞室，半径取为5.62 m。强烈大变形地段洞室形状及支护如图19所示。

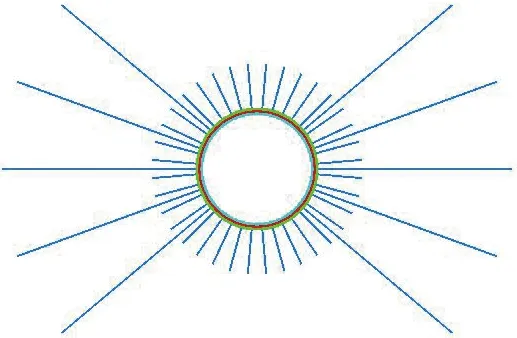
图19 强烈大变形地段洞室形状及支护Fig. 19 Cavern shape and support in extremely-large deformation

经试算，强烈大变形地段采用2层支护且及早施作时能满足验算，但考虑结构长期安全储备及施工时空条件，所以强烈大变形地段的支护拟选用3层支护，具体参数如下。

1)1层支护： 25 cm厚C25喷射混凝土+HW175@1.0 m和4.0 m长φ25砂浆锚杆@1.0 m×0.6 m(环×纵)，等效支护抗力分别为449.5 kPa和370.1 kPa，4 d(u=11.89 cm)后施作18 m长锚索@2.0 m×0.6 m(环×纵)。

2)2层支护： 20 cm厚C25喷射混凝土+HW175@1.0 m，等效支护抗力为372.5 kPa，开挖8 d(u=16.47 cm)后施作。

3)3层支护： 20 cm厚C25喷射混凝土+HW175@1.0 m，等效支护抗力为372.5 kPa，开挖12 d(u=17.88 cm)后施作。

该过程的围岩与支护相互作用曲线如图20所示，最终变形值为18.89 cm，小于3u*，说明该支护参数满足承载能力要求。实际工程中，建议采用预留第3层支护空间的方式，或采用长强快锚索(杆)主动控制，以达到减少初期支护层数、控制变形的目的。

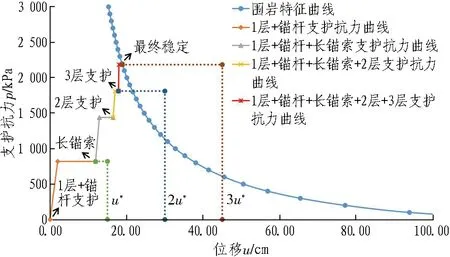
图20 强烈大变形地段围岩与支护相互作用曲线Fig. 20 Interaction relationship of surrounding rock support for extremely-large deformation

4.5 预留变形量

隧道初期支护预留变形量为预估的每一层初期支护变形量×富余系数(1.2～1.5)。根据上述分析，同时考虑不同开挖工法下封闭距离的差异，常规施工采用台阶法，相比计算简化的全断面开挖取1.5～2.0倍放大系数，得到不同等级挤压性大变形隧道的预留变形量，如表10所示。

表10 不同等级挤压性大变形隧道预留变形量Table 10 Reserved deformation of tunnels with different large extrusion deformation cm

5 案例分析

兰渝铁路木寨岭隧道全长19.1 km，最大埋深约为715 m，最大水平主应力为32.03 MPa，最小水平主应力为18.73 MPa，属高—极高地应力区。隧址区地质条件复杂，岩体节理裂隙发育，导致隧道围岩稳定性差，极易产生大变形，尤其是断层带岭脊核心段大变形问题特别突出。

为有效控制岭脊核心段极严重变形，采用圆形断面+3层初期支护的结构形式，具体支护参数为[20-21]： 第1层支护33 cm厚C30喷射混凝土，全环H175钢架@0.7 m。第2层支护25 cm厚C30喷射混凝土，全环H175型钢@0.7 m，并与第1层初期支护钢架交错布置；边墙设R38N自进式锚杆，长8 m，10根/环，纵向间距0.7 m，边墙设4×15.2 mm锚索，长15 m，10根/环，环距1.4 m。第3层支护40 cm厚C40钢筋混凝土(或格栅钢架喷射混凝土)。

通过分析得到第1层支护的等效支护抗力为510.4 kPa；第2层支护的等效支护抗力为435.4 kPa，长锚杆的等效支护抗力为396.3 kPa，长锚索的等效支护抗力为621.2 kPa；第3层支护的等效支护抗力为563.6 kPa。

围岩与支护相互作用曲线如图21所示。由图可知，该支护参数满足承载能力要求，验证了依据本文方法选取支护参数的合理性。

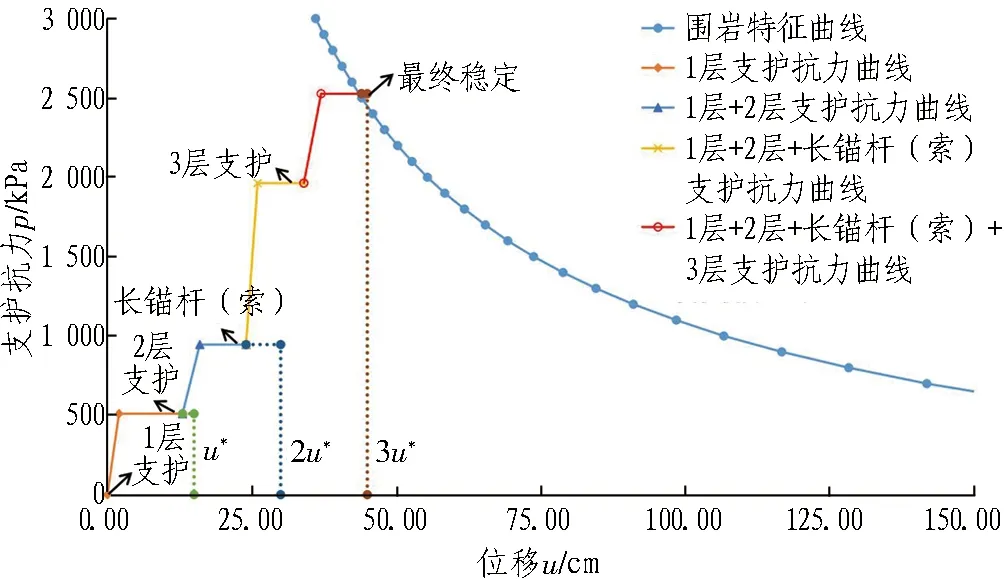
图21 木寨岭隧道断层带岭脊核心段围岩与支护相互作用曲线 Fig. 21 Interaction relationship of surrounding rock support in Muzhailing tunnel

6 结论与讨论

针对挤压性大变形隧道，考虑隧道开挖后的流变效应，分析分层支护对围岩变形的控制效果，对不同等级挤压性大变形隧道的适宜支护形式进行研究，得到以下主要结论。

1)不同变形等级挤压性大变形隧道支护形式分析结果表明，基于支护等效抗力分析、围岩与支护相互作用曲线的方式确定的分层支护模式在挤压性大变形隧道支护中是可行的。

2)基于荷载结构法和位移等效原则可量化分析不同初期支护参数能够提供的等效支护抗力，根据监测数据可反演分析流变参数，并根据流变分析确定不同支护的施作时机。

3)计算得到不同变形等级的挤压性大变形隧道支护建议参数与分层形式： 轻微大变形可选用1层初期支护+短锚杆的支护形式；中等大变形可选用2层初期支护+短锚杆的支护形式；强烈大变形可选用圆形隧道+3层初期支护+短锚杆+长锚索的支护形式。

本文初步提出了挤压性大变形隧道分层支护的思路，并给出了不同变形等级挤压性大变形隧道的支护参数和支护时机的建议。然而，在实际工程中，隧道埋深和地应力环境不尽相同，需在此基础上进行针对性分析，以确定适宜的支护参数与时机。