基于神经网络PID算法的供热控制系统仿真研究

董帅帅，高晓红

（吉林建筑大学，吉林长春， 130000）

0 引言

进入21世纪以来，环境问题愈发引起人们的关注，雾霾、PM2.5等词也逐渐进入人们的视野。在如今倡导绿色可持续的发展口号下，传统的燃烧煤炭等资源的供热方式显然不符合时代主题。而太阳能作为一种新型能源，不仅符合绿色可持续发展观，而且不会造成环境污染。在控制系统中，PID控制方案是其中比较典型的，但是随着时代进步，传统的控制方案逐渐满足不了控制要求，所以，不断有新的控制方案被各个领域的专家以及学者提出。其中人供神经网络控制、模糊控制和遗传算法控制等，在新的控制方法中被普遍应用。人工神经网络是模拟生物的神经系统，是神经元的集合，它的提出是受到生物神经网络的启发，人工神经网络通过多个神经元的信息传递与记忆，能够像人一样具有学习能力和处理复杂问题的能力。把人工神经网络与PID控制系统结合起来，既保证了PID控制器的稳定性，又能吸收神经网络的学习性自主性优点，有效的避免了传统供热控制系统控制过程中遇到的难题。

对于传统供热控制系统，时变性、大滞后性和非线性等是温度控制的特点，而基于人工神经网络的自主性特点，结合PID控制，得到一种基于神经网络的PD控制器[1]，实现控制系统的温度控制，应用于实际供热控制系统中，具有比较好的控制效果。

1 建立系统的传递函数

■1.1 供热控制系统

通过查阅资料，我们确定采用太阳能对对加热为主，电加热为辅助的供热方式，为了系统运行高效，对整个供热控制系统进行功能划分。首先是集热部分，顾名思义，集热部分主要是对供热用水进行加热，通过收集太阳能，将水箱中的水温升高。通过温度传感器、光照度传感器来收集数据在集热部分，其中温度传感器被用来判断水温是否达到预设供热值，光照度传感器来判断外界天气情况，若水温达到设定值则将其送至水箱中储存备用。集热部分、供热部分和换热部分和控制中心是该供热控制系统的四个主要组成部分；在换热部分，我们收集来自集热部分的热水，然后判断是否达到供热条件，利用换热器对一次侧热水和二次侧热水进行换热，换热效果通过冷热水的热交换体现。但是换热效率不能保证，因此为了换热效率的控制，我们加入变频器，换热效率由变频器的频率决定，从而更加精准的实现二次侧水温的控制。供热部分主要是在一二次侧冷热水进行热交换后，将达到供热条件的二次侧热水输入至用户，来改变用户的环境温度。整个过程是通过控制部分来实现，系统的整体调控是通过PLC为控制器进行控制。系统原理图如图1所示。

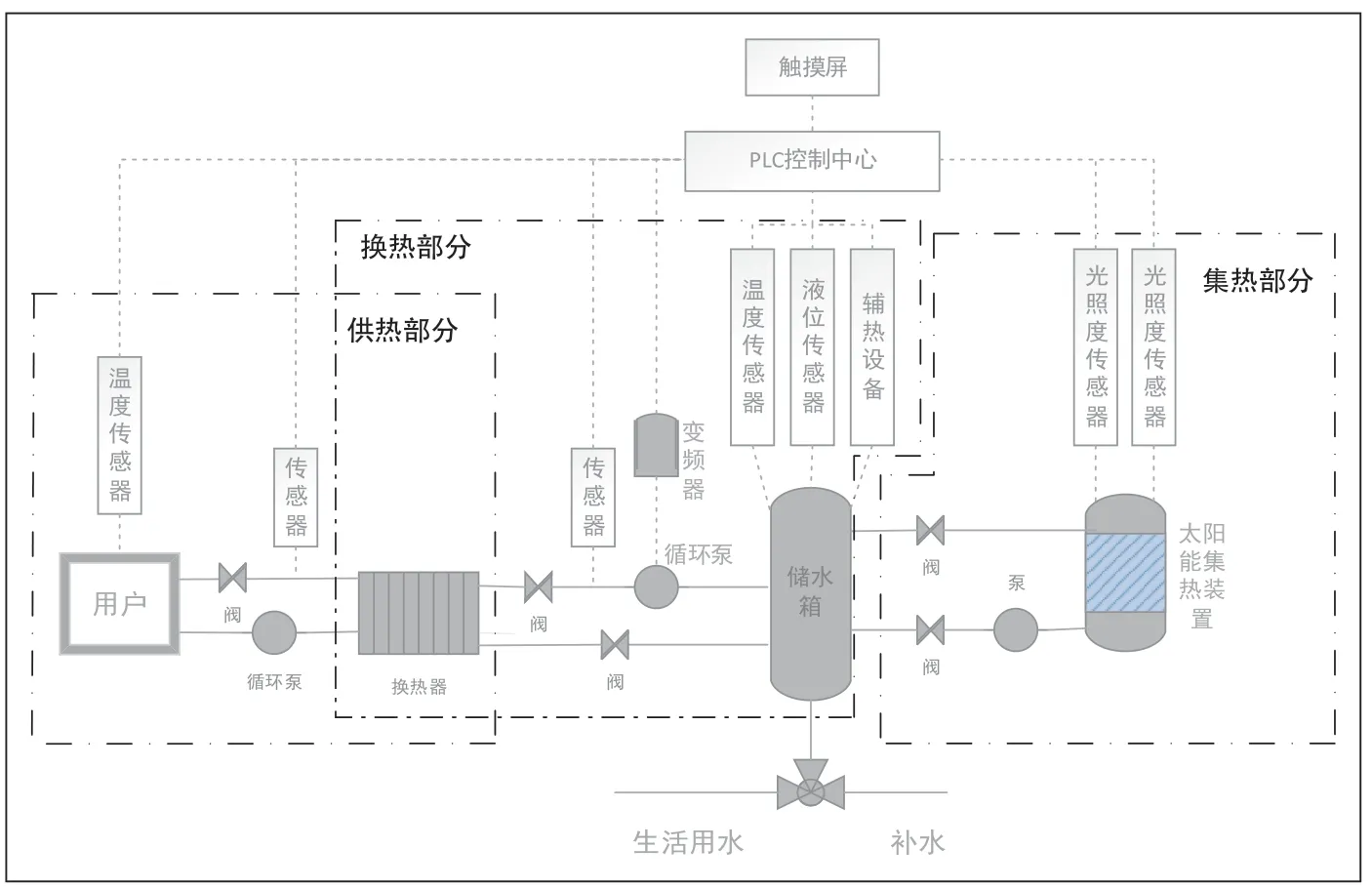
图1 供热控制原理

■1.2 控制原理

图2为神经网络PID控制原理。确定输入值，神经网络不断对PID的三个参数进行学习优化，最终确定控制器的三个参数比例（KP）、积分（KI）、微分（KD）的最优解，改变PID控制器的参数，最终实现对输出值的控制[2]。其步骤为：

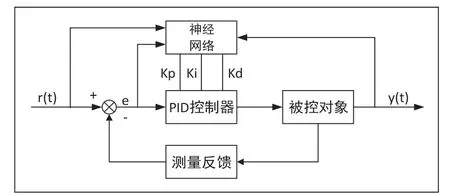
图2 基于神经网络PID控制原理

（1）根据控制要求，确定BP神经网络的基本结构，即：输入层、输出层、隐含层的节点数目，并且给定各层的初始化参数。

（2）根据被控参数的实际值与设定的基准值进行比较，并计算其偏差e；

（3）根据上述步骤中所得到的偏差值将其作为神经网络层的输入值，BP神经网络根据此输入值自主学习获得PID控制器的Ki、Kp、Kd三个参数的最优化值；

（4）PID 控制器根据得到的Ki、Kp、Kd三个参数进行计算获得控制器的输出值[3]；

（5）调整神经网络权值，对PID控制器参数的自适应调整；

（6）循环计算。

■1.3 传递函数的建立

在传统的供热控制系统中，我们的主要参数为温度，除此之外还有水压等参数。基于神经网络PID的供热控制系统主要是通过变频器改变循环泵的工作频率对换热效率进行控制，最终达到温度控制的目的。通过查阅资料，典型的工业控制系统中，温度控制系统大多为一节系统，为了减少误差，我们排除一些外界因素，如设备因素后，最终确定分系统为供热控制系统的传递函数模型可以看作是一节惯性加纯延时系统。其传递函数如式(1)所示：

式中：K—对象的放大增益；T—对象的时间常数；τ—对象的纯滞后常数。

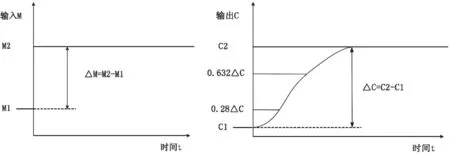
图3 一阶惯性纯滞后对象响应曲线

传递函数的确定方法有很多，比如频率法和根轨迹法，对于一阶惯性环节串联上纯滞后环节，我们通过根据Cohn--Coon（科恩-库恩)公式来确定相应参数。

根据公式有：

式中：ΔM—系统阶跃输入；ΔC—系统的相应输出响应；t0.28—为温度上升到0.28ΔC时的时间；t0.632—为温度上升到0.632ΔC时的时间。

在供热控制系统中，不同频率下，系统的输入如图4所示。

图4为供热控制系统不同频率下的输入的阶跃曲线，所以根据Coon Cohn公式可得：

图4 不同频率下系统的输入的阶跃曲线

式中，M终和M初分别为各频率下的系统输入最终值和输入初始值。

图5输出温度与时间关系曲线初始值与最终值，通过测得系统的温度变化曲线，以20Hz时温度变化为例。

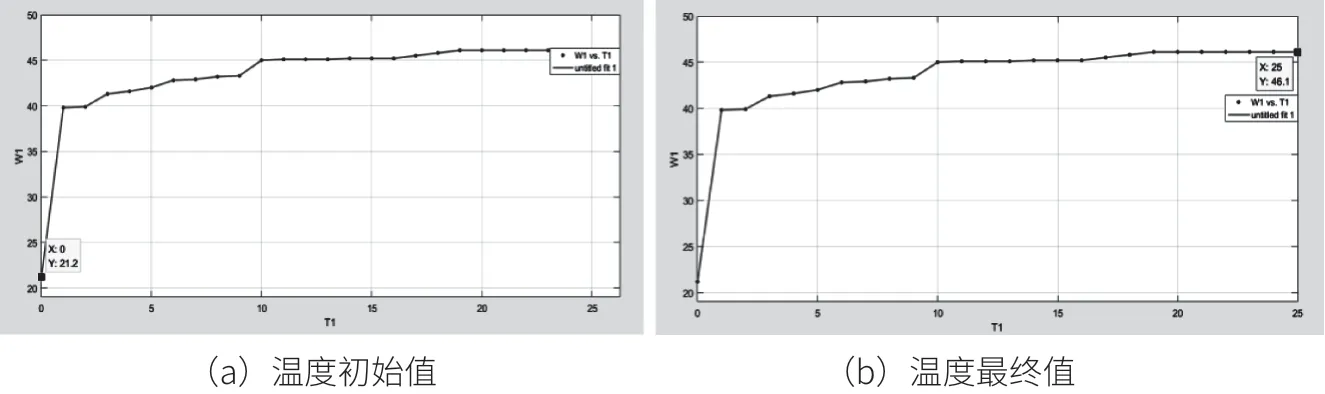
图5 输出温度与时间关系曲线初始值与最终值

通过科恩-库恩公式我们可以得到：

图6 输出温度与时间关系曲线

由图5、6知，对应ΔC处的时间为：t0.2822.5s;t0.632=50.8s;可计算出一阶延迟传递函数的两个时间参数如下:

则控制系统的传递函数可表示成：

同理，30Hz和40Hz时，控制系统的传递函数为：

分别对不同频率进行多次实验，计算得出传递函数，最终求其平均值之后得系统的传递函数为：

2 神经网络结构

神经网络是模拟生物的神经系统，是神经元的集合，它的提出是受到生物神经网络的启发，人工神经网络通过多个神经元的信息传递与记忆，能够像人一样具有学习能力和处理复杂问题的能力,在神经网络中，任意两个神经元节点之间的连接信号表示为信号传递的加权值[5]。图7单神经元示意图。图中Xa...Xn为神经元的输入信号，ωa...ωn为权值，Y为输出。

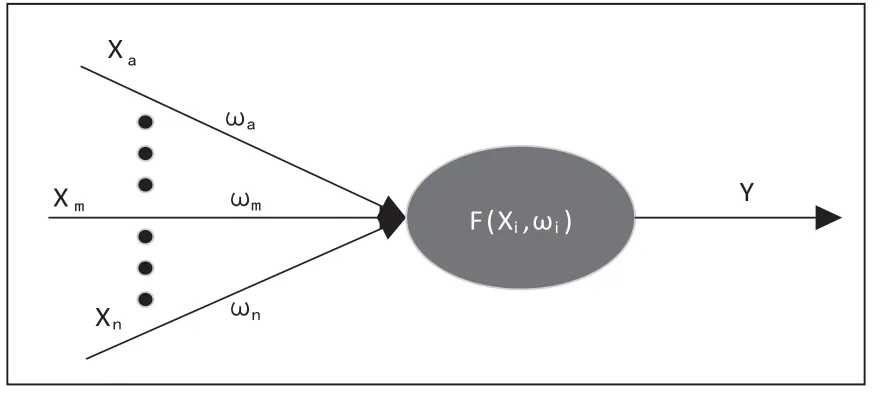
图7 单神经元示意图

神经网络是对生物脑部的简化。脑部神经元数量相当庞大复杂，不可能一丝不差的还原出来，所以通过脑模型抽象简化，我们得到了现在所熟知的神经网络控制算法。因为这种该算法的优点，它广泛应用于智能控制、自动控制和医学等领域。

3 神经网络PID控制器的模型搭建与仿真

■3.1 神经网络的训练

打开MATLAB，可以通过“应用程序”选项选择神经网络工具箱，除此之外我们可以输入命令直接调用神经网络工具箱[5]。打开工具箱页面后将数据导入相应区间，调整好参数后将建立的fis文件保存。一个良好的神经网络控制系统，我们期望误差为零，为了使训练误差减小，将训练周期设为1000，最终数据的训练输出结果曲线如图8所示。

图8 训练数据收敛曲线

根据图8可知，当训练周期结束后，其输出结果为：Kp的误差为0.848；Ki为0. 097837；Kd为0.11473。误差结果几乎趋近于零，控制在较低范围内，所以满足供热控制系统的控制需要。

训练结束后需要导入数据进行验证，其验证结果如图9所示。

图9 验证数据结果示意图

■3.2 仿真模型

将训练后的数据保存后导入到MATLABA的工作区间，通过S函数建立神经网络控制器的模块，设计了神经网络PID控制仿真器，并基于神经网络原理图，在Simulink中构建了基于神经网络的供热控制系统的控制仿真模型，仿真时间300s,采样周期设置为0.01s，系统的输入峰值为45的阶跃信号。

仿真系统的输入为误差e和误差变化率ec,根据误差即误差变化率，系统会不断地改变权值系数，调节输出参数，是输出值一直在最优值范围，是系统达到稳定。

■3.3 仿真结果

在把设置好参数后，仿真得到系统的阶跃响应曲线如图11所示。

从图11可以看出:相较于传统PID控制系统，神经网络PID到达稳定时间较快，超调量减小，最大误差较小，达到了预期效果。

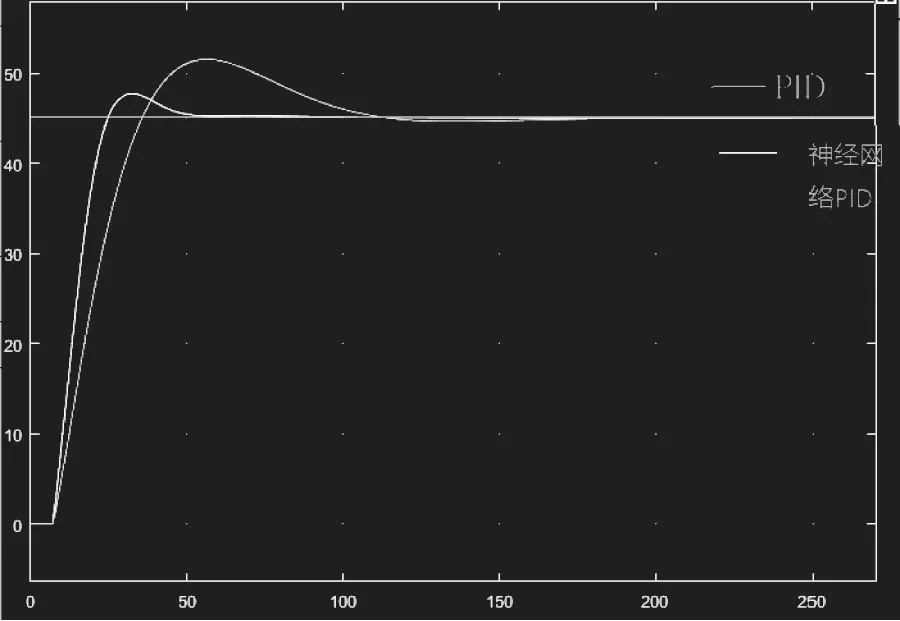
图11 系统位移阶跃响应曲线对比

4 结论

通过MATLAB软件中的Simulink模块，搭建系统的控制模型，为了与传统的控制方式作比较，增加了传统PID控制方式的仿真模型，经过参数调整后，我们得到了传统PID控制方式和神经网络PID控制方式的仿真结果，结果表明: 神经网络模PID 控制策略优于PID控制，在稳定性方面，相较于传统PID控制，神经网络PID控制稳定性好，提前了63s，其超调量从14.5%下降到6.1%，减小了8.4%。结果表明在在温度控制系统中，神经网络PID控制控制效果良好。

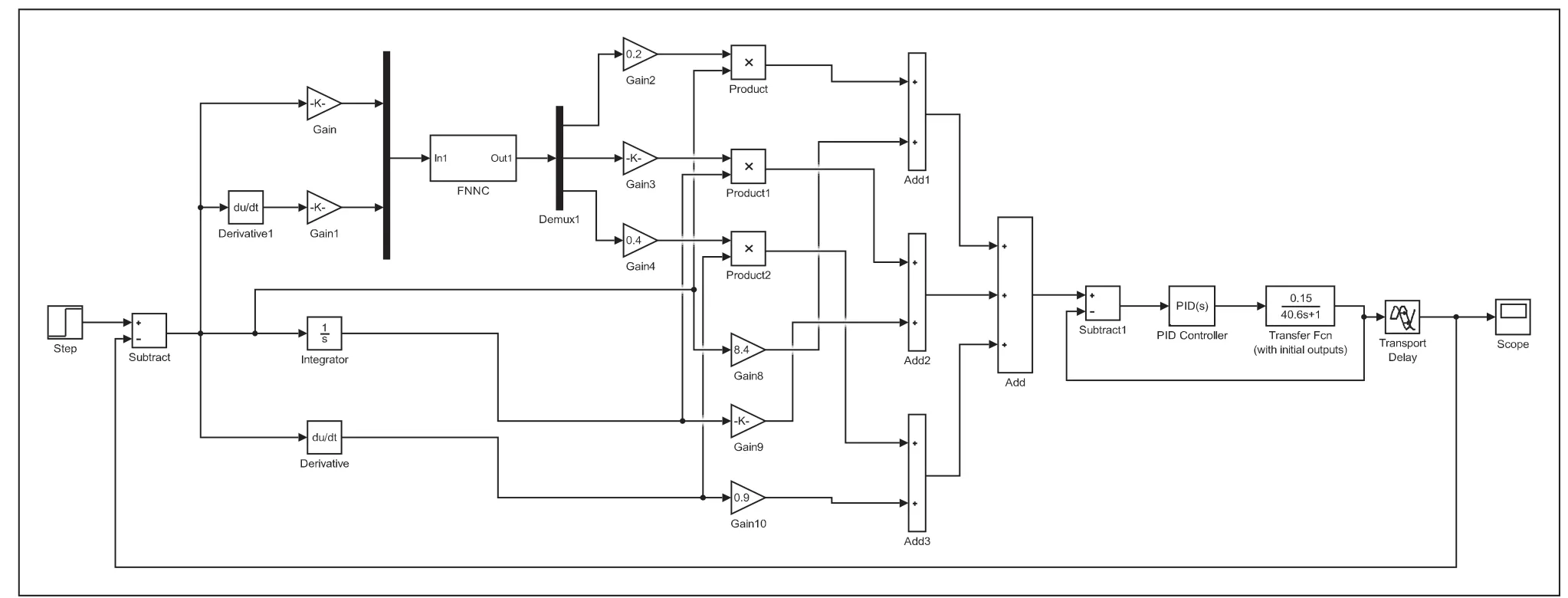
图10 神经网络PID仿真模型