基于松散型WNN 的运动想象脑电信号解码研究
胡秀枋,何 爽,邹任玲,张一凡,毛晨罡,黄 鑫,李 丹,曹 立
(1 上海理工大学健康科学与工程学院,上海 200093; 2 上海市第六人民医院,上海 200233)
0 引 言
脑机接口技术(Brain-Computer Interface,BCI)是一种脑部神经和外部设备直接进行交互的系统,可以达到直接控制外部设备的目的[1-2],目前已应用于睡眠与癫痫的检测[3-5]、抑郁症识别和情感识别[6-7]以及运动想象[8]等方面。 其中,运动想象脑电信号解码在实时BCI 应用中有重要的临床意义。
目前,基于运动想象脑电信号解码很热门,取得较大的进展。 其中,Andrade 等学者[9]使用主成分分析法对特征值进行处理,并使用支持向量机(Support Vector Machine,SVM)进行单次试验的左右手抓球分类,得到了70%的平均准确率。 刘冲等学者[10]利用SVM 对二分类数据集进行分类,得到的分类准确率为82.86%。 WANG 等学者[11]提出支持向量机-典型相关分析-信道选择算法(SVMCCA-CS),对二分类的数据集选择权重最大的通道,平均准确率可达80.03%。 但深度学习也逐渐被大量应用在脑电信号的解码中。 Tang 等学者[12]基于EEG 的时空特征,建立5 层卷积神经网络模型对左手和右手的二分类MI EEG 进行解码,得到了86.41%的平均准确率。 Shahtalebi 等学者[13]基于CNN 提出一种Siamese 结构,对四分类的平均准确率为73.21%。 Chen 等学者[14]提出一种滤波器组空间滤波和时空卷积神经网络(FBSF-TSCNN)的方法,其中FBSF 模块将原始信号转换为合适的EEG表示,TSCNN 对其进行分类,并提出了一种新的分段训练策略,平均准确率有一定的提高。
松散型的小波神经网络(Wavelet Neural Network,WNN)是将小波分析和神经网络分开计算再进行组合,在故障的模式识别、时间序列预测等方面应用比较成熟。 本文提出将松散型小波神经网络(Wavelet Neural Network,WNN)应用于运动想象多分类的解码研究中,使用双树复小波提取脑电信号特征,为神经网络提供特征向量,进行训练,完成分类,讨论解码效果。
1 数据集描述及预处理
1.1 数据集描述
数据集是格拉茨科技大学所提供的BCI Competition IV 的数据集2a[15]。 该数据集包含有9个受试者的EEG 数据,采样频率为250 Hz,为四分类数据集,其中分别为左手、右手、脚和舌头。 单个受试者训练与测试共计进行了576 次试验,每类动作想象均为144 次。
在t =0 s 时,屏幕上出现十字并伴随哔(Beep)的一声,提醒受试者开始准备;在t =2 s 时,屏幕上出现指向不同方向的箭头,分别指向左、右、下或上(对应于左手、右手、双脚或者舌头四个动作中的一个),在屏幕上停留的时间为1.25 s,并没有进行反馈。t =6 s 时,运动想象任务结束,持续时间为3 s左右。 受试者有短暂的休息时间,并等待下次实验的开始。 单次实验的实验范式如图1 所示。

图1 运动想象实验范式时序图Fig. 1 MI experimental paradigm timing diagram
1.2 数据集预处理
由于数据的通道名的缺失,按照国际10/20 系统的方式对信号进行命名。 受试者在执行运动想象任务包括想象肢体或者舌头上的运动存在ERS 和ERD现象,且主要存在于alpha (8 ~12 Hz)和beta (13 ~30 Hz)[16]。在特征提取前,对信号进行简单的预处理,首先提取有效的脑电信号即3~6 s 的脑电数据和去除眼电通道的数据,对信号进行8~30 Hz 的带通滤波,以此提高信号的信噪比,并进行重参考等操作。
2 特征提取及分类器
2.1 特征提取
双树复小波变换(Dual-tree Complex Wavelet Transform,DTCWT)是Kingsbury[17]在2001年提出的一种对离散小波变换的改进的小波变换,是对小波变换的延伸。 弥补了离散小波变换移位方差、方向性差和缺乏相位移动等缺点,通过二叉树结构的两路滤波器对信号进行分解与重构,其中包括实部与虚部,可以想象为2 个并行的小波变换,如图2 所示。 图2 中,h0(n) 和h1(n) 表示共轭正交滤波器对,g0(n) 和g1(n) 表示共轭积分滤波器对,↓2 表示隔点采样。 虚部的采样信号为实部二抽取所丢失的值。 函数表达式为:

图2 双树复小波结构Fig. 2 Dual-tree complex wavelet structure
其中,φ(t) 是输入信号,φh(t) 和i φg(t) 分别是复小波的实部与虚部。
提取特征时,使用Python 中的DTCWT 库将脑电信号分解为4 个级别。 对每个复小波系数计算平均值、DTCWT 系数的平均功率、标准差和子带比,将其进行组合构建特征矩阵。 因此得到的特征矩阵大小为22×4×5(通道数×特征×DTCWT 系数),将其转换为1×440 的矢量进行分类。
2.2 松散型小波神经网络
小波神经网络(Wavelet Neural Network,WNN)是将小波分析与人工神经网络相结合而提出的一种网络结构。 主要是使用非线性的小波基取代了通常的非线性函数,解决了一般神经网络结构的一些非线性优化问题。 WNN 是Zhang 等学者[18]于1992年提出的基于小波分析的神经网络,使用小波函数作为超参数。 WNN 是一种基于小波分析理论和小波变换的多分辨率的人工神经网络。 小波神经网络的输出值计算公式为:
其中,φ表示小波函数;x表示输入向量;m表示输入数量;λ表示隐藏层的数量;ω表示网络权重。
松散型WNN 中,将小波分析和神经网络分开计算再进行组合,前者为神经网络输入特征向量,二者紧密相连,却又相对独立,具体结构如图3 所示。 随着深度学习技术的不断发展,适当增加隐藏层的深度可让松散型WNN 与紧密型WNN 性能相差无几。

图3 松散型WNNFig. 3 Loose WNN
3 结果与分析
本研究硬件环境采用16 GB 内存(RAM),AMD Ryzen 5 4600H 处理器的笔记本,编程语言为Python3.6,DTCWT 库为0.12.0。
3.1 不同分类器的比较
每位受试者在WNN 中的准确率见表1。 同时,利用SVM 和LGBM 两种经典的机器学习算法作为WNN 的对比实验,选出最优的分类器。

表1 基于DTCWT 的不同分类器解码结果Tab. 1 Decoding results of different classifiers based on DTCWT
由表1 可知,使用小波神经网络对脑电信号的解码效果最优,平均准确率达到了76.03%,比支持向量机的平均准确率高10.19%,比LGBM 的平均准确率高11.91%。 其中,WNN 中最高准确率比SVM和LGBM 分别高9.09%和12.38,最低准确率比SVM和LGBM 分别高11.15%和14.27%。 在3 种分类器中,WNN 在9 位受试者中的表现均属于最佳,每位受试者的准确率均高于SVM 和LGBM。 因此,WNN与SVM 和LGBM 相比,整体的分类性能更优越,是分类效果更好的分类算法,应用在不同的个体上波动范围更小,是一种有效的分类算法。
3.2 与现有方法的比较
为了验证WNN 的有效性,将在WNN 中得到的分类结果与现有方法的分类准确率进行了比较,具体结果见表2。

表2 与现有方法的比较结果Tab. 2 Comparison results with existing methods
由表2 可以看出,本文方法仅有A06 的准确率低于EEGNet;FBSF+TSCNN 中只有A01 和A09 高于所提出的方法;Siamese NN 中也只有3 位受试者高于本文提出的方法,即A01、A06 和A09;多特征+CNN 中A01、A02、A03 和A06 高于本文提出的方法,但其它5 位受试者都比本文方法低。 其中,本文所提出的算法的最低准确率均高于其它4 种方法,最大准确率只比多特征+CNN 低0.02%。 另外在各个方法中A01、A03、A07 和A08 的准确率均高于其他几位受试者。 各方法的分类识别准确率如图4 所示,从中可以看出,相比于其他文献中的解码方法,本文方法的平均准确率更高,达76.03%;解码效果更好,具有一定的优势,符合当前分类结果的主流趋势。
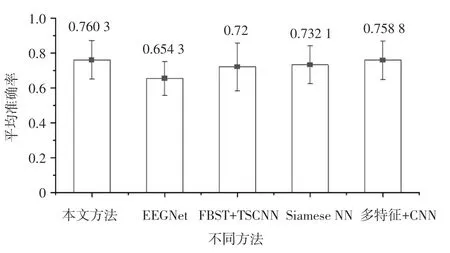
图4 各方法四分类识别准确率Fig. 4 Accuracy of each method IV classification recognition
4 结束语
本文提出将松散型小波神经网络应用于运动想象脑电信号的分类当中。 DTCWT 作为常规神经网络的前置手段,为神经网络提供特征向量。 使用DTCWT 对预处理后的脑电信号进行分解,对分解后的复小波系数进行特征提取,计算平均值、平均功率、标准差和子带比,构建特征向量并送入到神经网络进行分类,可以一定程度上提高运动想象的分类准确率,最终在BCI Competition IV 2a 得到的平均准确率为76.03%;与不同分类器比较,WNN 分类效果较好。 在此基础上,和现有的EEGNet、FBST +TSCNN 及多特征融合+CNN 等方法进行了比较分析,结果良好。 因此,基于DTCWT 的松散型小波神经网络在运动想象分类中是有效的,为运动想象解码研究提供了一种新的方法。

