基于全阶时间幂灰色预测模型的优化研究
孙竟耀,李 程
(上海工程技术大学航空运输学院,上海 201620)
0 引 言
灰色系统理论是针对信息不完全或不确定的系统的控制理论,自上世纪八十年代创立以来,完善了对“小样本数据”、“贫信息”的不确定性系统的研究。 随着研究的深入,GM(1,1)也开发出许多分支模型。 但是,为了解决GM模型在实际应用过程中对不同数据类型适用性低,预测精度不理想的情况,寄希望以不同的初始值优化方法和不同的背景值取值方式提高GM 模型的适应性和分析预测精度。 在背景值求解方式的优化方面,蒋玉婷等学者(2020)[1]在背景值的求解方式上将牛顿插值法和柯特斯公式相结合进行计算,并在实例验证中取得良好的效果。 王正新等学者(2008)[2]在非齐次指数序列拟合函数的基础上重新推导背景值表达式。蒋诗泉等学者(2014)通过GM 模型背景值几何意义的研究,给出了基于函数逼近理论和复合梯形公式的背景值优化公式。 张彬等学者(2013)[4]论证了基于背景值和边值协同优化对GM 模型的预测精度提升有效。 高媛媛等学者(2020)[5]通过将背景值调整为连续化后的原始序列函数,从而提高了灰色微分方程和白化方程的适配度,给出了新的优化思路。 王承庆(2017)[6]在正弦变换和误差最小化原理的前提下实现对GM 模型初始条件和背景值的优化,并在国内水产品总产量的预测问题上得到较好验证。 龙钊等学者(2021)[7]计算三参数重构背景值,并进一步引入二次项优化灰色作用量,实现了背景值和灰色作用量的综合优化。 张可等学者(2010)[8]基于粒子群算法对GM(1,1) 模型背景值系数动态寻优,实现了预测精度的提升。
同时,李守军(2018)[8]对GM(1,1) 优化的模型结构进行整合提炼,增加幂函数项得到全阶时间幂灰色预测模型FOTP-GM(1,1),在初始值序列的特征提取下实现模型结构和参数的动态改变,对近似非齐次指数序列具有较好的预测效果。 FOTPGM(1,1)模型较传统GM(1,1) 模型在结构上用幂函数结构替换常数项b,随着被模拟数列的特征变化,幂函数结构也随之变形为DGM(1,1)、NGM(1,1,k)、NDGM、SAIGM 等模型。 由此可见,FOTP- GM(1,1) 模型能够灵活变动结构,具有对不同序列数据的适应性。而FOTP- GM(1,1) 的背景值由于先连续化、后离散化的求解方式,因此在转换求解过程中必然存在误差,这也为预测精度的提升提供可能。
综上,本文将着重在拓展模型FOTP-GM(1,1)上进行优化,构建时利用智能算法对背景值的系数设定动态寻优,将背景值系数设定为0 到1 之间的变量,利用粒子群算法在对应区间内动态寻优,实现提高FOTP-GM(1,1)模型精度的目的。
1 模型基础及优化
1.1 传统GM(1,1)模型
定义1设非负原始序列为X(0)=(x(0)(1),x(0)(2),…,x(0)(n)),其中x(0)(k) ≥0,k =1,2,…,n则称X(1)=(x(1)(1),x(1)(2),…,x(1)(n)),其中:
称Z(1)为X(1)的紧邻均值生成序列,其中:
定义2设序列X(0),X(1)和Z(1)满足定义1,则GM(1,1)模型的基本形式为:
1.2 FOTP-GM(1,1)的建模与求解
定义 3设非负初始值序列X0={x(0)(1),x(0)(2),…,x(0)(n)},n∈N+对应的1-AGO 序列定义为:
背景值序列定义为:
其中,z(1)(k +1)=αx(1)(k)+(1-α)x(1)(k +1),k =1,2,…,n -1。
定义4根据定义3,给出全阶时间幂灰色预测的定义式:
其中,- a是模型背景值系数;bi(i =1,2,…,h) 是模型的灰色作用量;bith-i是模型的时间幂项;h为模型时间幂项的阶数。
定义5根据灰导数信息覆盖原理,这里定义FOTP-GM(1,1)模型的离散形式可转换为连续的微分方程形式,称之为FOTP-GM(1,1)模型白化方程:
就模型发展系数- a,灰色作用量bi的求解做出定义,若(a,b1,b2,…,bh)T是待估参数序列,则:
则FOTP-GM(1,1)模型的最小二乘估计满足:
根据参数估计结果,整理后FOTP- GM(1,1)模型的时间响应函数为:
在一阶累加序列x(1)(k) 和时间响应序列离差平方和最小的背景下,得模型最优迭代初值为:
为避免在参数求解过程中的矩阵病态性问题FOTP-GM(1,1)模型的阶数h有固定的上限值,通过计算实对称矩阵BTB的谱条件数cond(BTB)2。若cond(BTB)2|h =p <1012且cond(BTB)2|h =p+1>1012,则h =p。
2 FOTP-GM(1,1)模型背景值优化
2.1 FOTP-GM(1,1)模型误差分析
以2 阶模型h=2 为例,对定义5 中模型的式(8)白化方程在区间[k -1,k] 进行积分,并简化后得:
与式(13)的h =2 阶形式比较,可得:
根据积分的几何意义分析,背景值的实际值曲线应是底边长在区间[k -1,k] 上的曲边梯形面积,而实际计算过程中因微分方程的求解过程中存在的误差,此为误差来源。
2.2 动态背景值a 粒子群算法寻优
粒子群算法(PSO)最早启发于人类对鸟类觅食行为的思考,鸟类以单一个体进行单独觅食,在一定区域内搜寻最近的食物位置,利用自身经验判断最佳位置,并在判断的过程中不断与鸟群共享信息,使得鸟群最终找到最佳觅食位置。
粒子群寻优算法的核心公式如下:
其中,ω是惯性因子,旨在对粒子的局部最优和整体区间最优两者进行权重协调;c1和c2是分别是学习因子1 和2,学习因子调节每个粒子在寻优过程中的检索步长;r1和r2为存在于[0,1]区间的随机数。 综合上述定义,粒子群寻优算法中,粒子群中由m个粒子组成的X =(x1,x2,…,xm),第i个粒子在空间中的位置表示为Xi =(xi1,xi2,…,xim),单一粒子寻优速度为Vi =(vi1,vi2,…,vim)T,每个粒子单体最佳位置为Pi =(pi1,pi2,…,pim)T,整体寻优后的最优位置为Pg =(pg1,pg2,…,pgm)T。
在模型的常规求解过程中1-AGO 背景值序列系数a通常取值0.5,这种赋值情况经过诸多案例证明可以得到较为理想的预测精度,但赋值仍缺少有力依据。因此在FOTP- GM(1,1) 模型的背景值划定取值范围在[0,1]区间,利用粒子群算法在区间内进行寻优。
寻优依据为计算输出模拟数据的平均相对百分误差(MAPE),以平均相对百分误差最小值为筛选标准,MAPE计算公式为:
3 实证分析
FOTP-GM(1,1)模型可以完成对存在指数变化规律的序列数据进行模拟预测。 本节将在四阶FOTP-GM(1,1)模型的基础上参考李守军[1]设定的4 组典型指数序列进行实证分析。 数据序列包括齐次指数序列,带有常数项的非齐次指数序列、带有速度项和常数项的非齐次指数序列以及带有加速度、速度和常数项的非齐次指数序列、实证分析环节将上述四种序列数据类型均作为输入数据在传统GM(1,1)模型和四阶FOTP-GM(1,1)模型进行模拟,然后利用粒子群算法在[0,1]范围内对四阶模型进行背景值系数寻优,最后对4 种模型的模拟数据和预测数据计算平均相对百分误差并综合比较,论证背景值优化后的模型预测精度。
3.1 初始数据处理
(1)设定齐次指数序列X1:x(0)=0.9×1.8k,k =1,2,…,15。X1数据序列k =1,2,…,10 作为初始值数据用于建模,经1-AGO 后得到序列X(1)1 ,紧邻均值系列Z(1)1 :
(2)设定带常数项非齐次指数序列X2:x(0)=1.2×1.9k +1.5,k =1,2,…,15。X2数据序列k =1,2,…,10 作为初始值建模,经1-AGO 后得到序列,紧邻均值系列:
(3)设定带有速度项和常数项的非齐次指数序列X3:x(0)=1.6×2.1k +0.5k +1.2,k =1,2,…,15,X3数据序列k =1,2,…,10 作为初始值建模,经1-AGO 后得到序列,紧邻均值系列:
(4)设定带有加速度、速度和常数项的非齐次指数序列X4:x(0)=1.2×1.5k +0.3k2+1.5k +1.1,k =1,2,…,15。X4数据序列k =1,2,…,10 作为初始值建模,经1-AGO 后得到序列,紧邻均值系列:
3.2 模型参数估计与背景值寻优
得到上述数据后,运用式(9)建立矩阵Y和B利用最小二乘估计法求解(a,b1,b2,b3,b4)T=BTB-1)BTY得到模型参数,经粒子群算法寻优后背景值参数见表1。

表1 四阶FOTP-GM(1,1)模型参数估计表Tab. 1 Parameter estimation table for the fourth-order FOTP-GM(1,1) model
3.3 模型精度对比
将参数估计结果和粒子群算法寻优后,利用得到的优化后的背景值系数带入建模分析。 划定序列数据k =1,2,…,10 为初始值测试集数据,k =10,…,15 为预测集数据。 4 组指数序列数据经过传统GM(1,1)模型FOTP-GM(1,1)模型和基于背景值改进的FOTP-GM(1,1)模型,计算模拟数据和预测数据相对误差,对k =1,2,…,15 模拟相对误差计算平均相对模拟百分误差,计算结果整理见表2 ~表5。

表2 齐次指数数序列计算结果Tab. 2 Calculation results of chi-square exponential number series
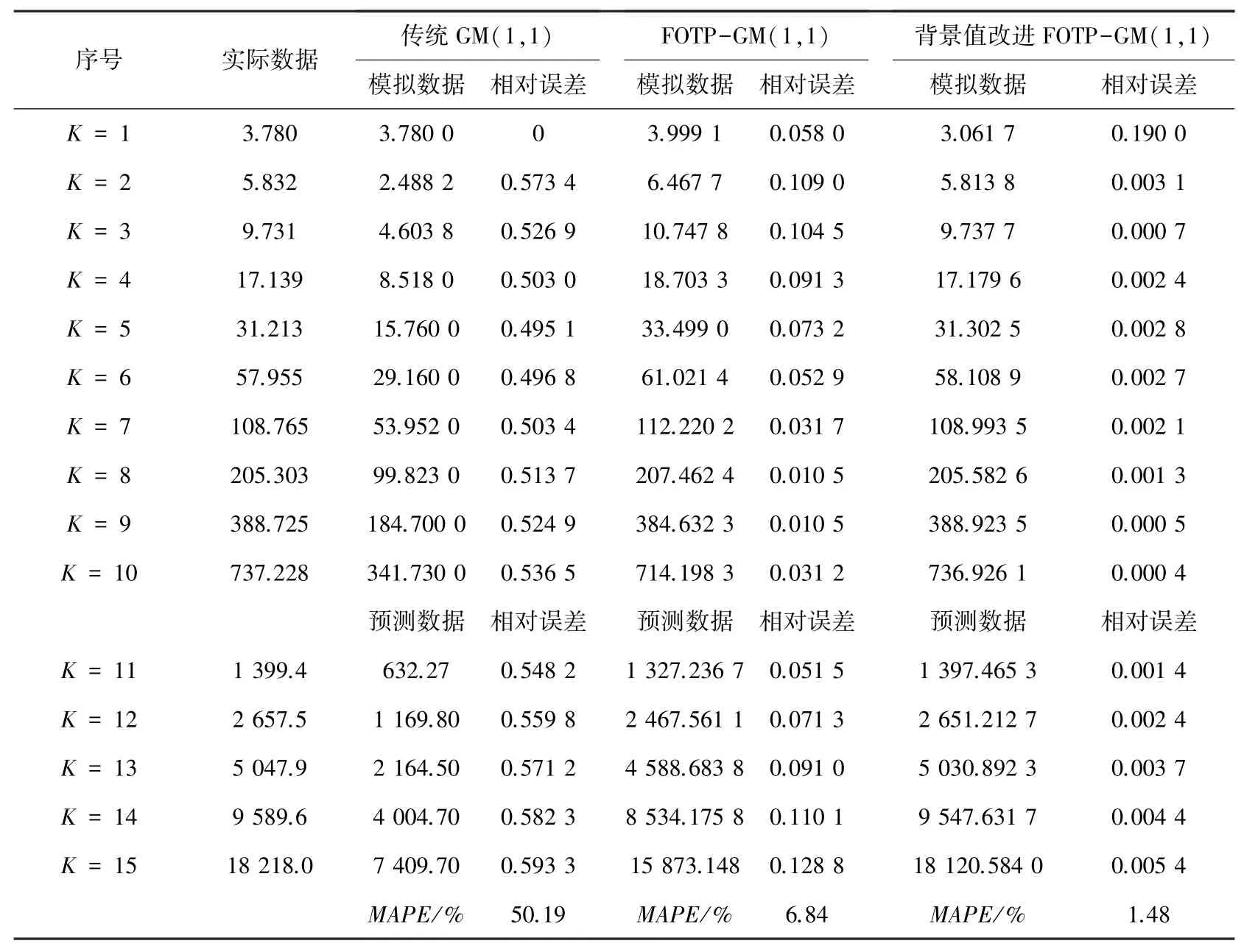
表3 带常数项的非齐次指数数序列计算结果Tab. 3 Calculation results of non-simultaneous exponential number series with constant terms
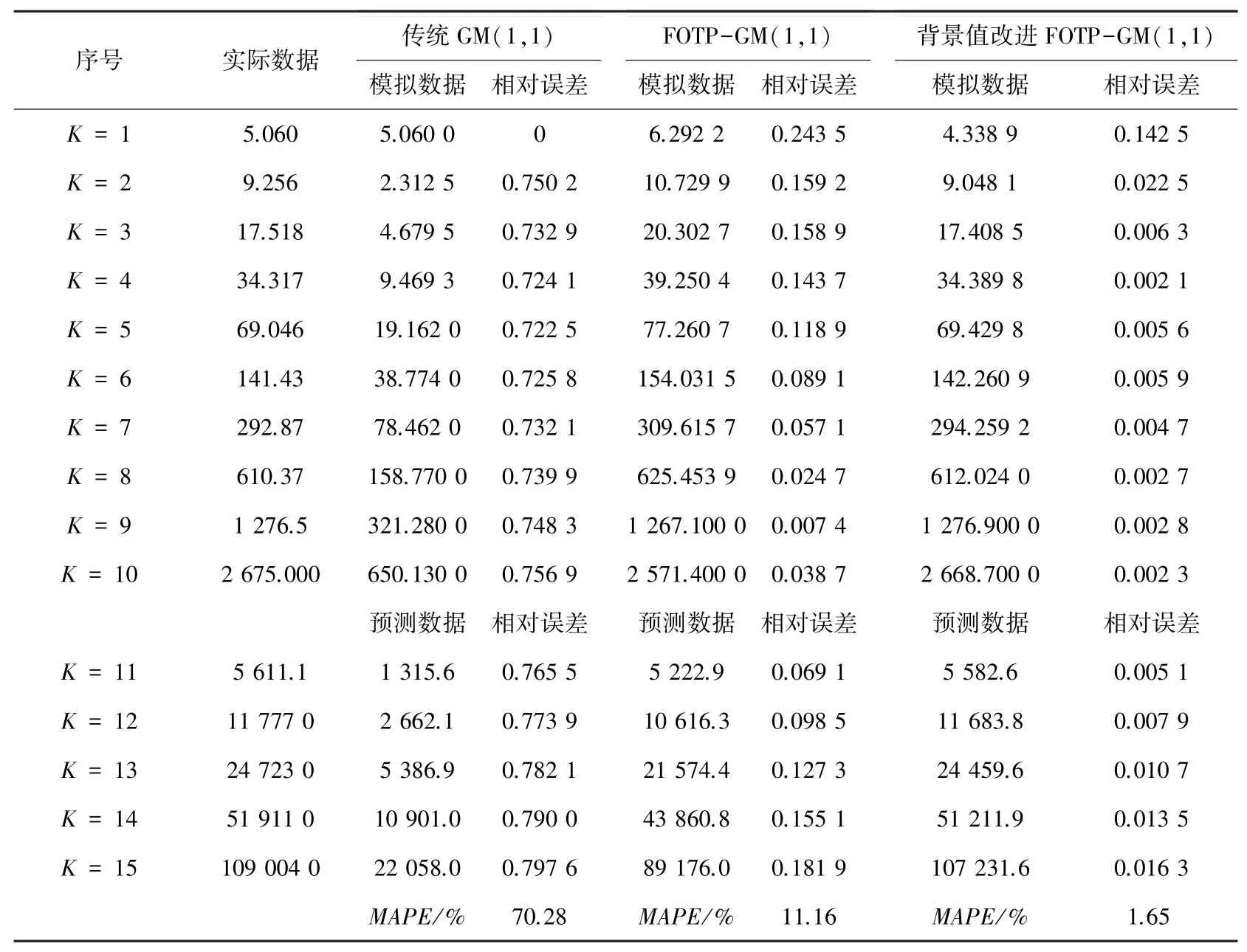
表4 带速度项和常数项的非齐次指数数序列计算结果Tab. 4 Calculation results of non-simultaneous exponential number series with velocity term and constant term

表5 带加速度、速度、常数项的非齐次指数序列计算结果Tab. 5 Calculation results of non-simultaneous exponential series with acceleration,velocity,and constant terms
从上述表2~5 可以分析得到,经过背景值优化后的四阶FOTP-GM(1,1)模型在预测精度上得到明显提高,齐次指数序列预测精度较前2 种模型精度分别提高了98.37%和97.15%;带常数项非齐次指数序列预测精度较前2 种模型精度分别提高了97.05%和78.36%;带速度项、常数项非齐次指数序列预测精度分别提高了97.65%和85.21%;带加速项、速度项、常数项非齐次指数序列预测精度提高了19.64%和40.37%,精度均得到了显著提升。 将3 种模型按照输出结果绘制模拟数据序列曲线和相对误差曲线如图1~图8 所示。

图1 3 种灰色模型对齐次指数序列模拟曲线Fig. 1 Simulation curve of chi-square exponential series
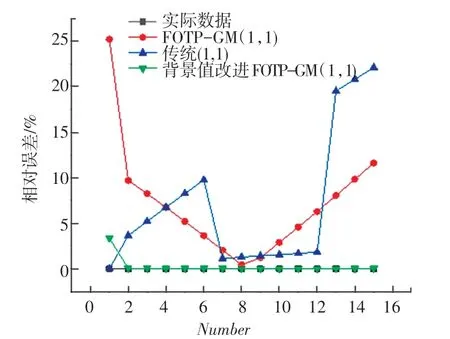
图2 3 种灰色模型对齐次指数序列模拟相对误差曲线Fig. 2 Simulation of relative error curves

图3 3 种灰色模型对带常数项非齐次指数序列模拟曲线Fig. 3 Simulation curve of non-simultaneous exponential series with constant terms
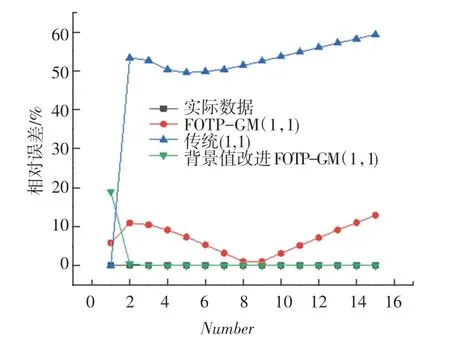
图4 3 种灰色模型对带常数项非齐次指数序列相对误差曲线Fig. 4 Simulation of relative error curves

图5 3 种灰色模型对带速度项、常数项非齐次指数序列模拟曲线Fig. 5 Simulation curve of non-simultaneous exponential series with velocity term and constant term

图6 3 种灰色模型对带速度项、常数项非齐次指数序列相对误差曲线Fig. 6 Simulation of relative error curves with velocity term and constant term

图7 3 种灰色模型对带加速度项、速度项和常数项非齐次指数序列模拟曲线Fig. 7 Simulation curve of non-simultaneous exponential series with acceleration,velocity and constant terrms

图8 3 种灰色模型对带加速度项,速度项,常数项非齐次指数序列相对误差曲线Fig. 8 Simulation of relative error curves with velocity term and constant term
从上述图1 ~8 分析可得背景值优化后的FOTP-GM(1,1)模型与实际曲线更贴合,相对误差曲线较传统GM(1,1)模型和FOTP-GM(1,1)模型波动更小,背景值优化效果得到体现。 通过精度对比,以误差精度小于10%为标准进行筛选,得数据序列类型与灰色模型之间的适配关系见表6。

表6 模型与数据类型适配表Tab. 6 Model and data type adaptation table
4 结束语
全阶时间幂灰色预测模型因为其自身的结构特点使得对近似非齐次指数特征的数据序列具有较好的预测精度。 但是在背景值构造过程中缺少理论依据,因此模型精度存在提高的可能。 本文将模型背景值α =0.5 更新为[0,1]内的动态值,利用粒子群优化算法在动态变化范围内按照相对百分误差最小为原则进行寻优,以寻求得到最合理的背景值α。得到最优背景值α后,带入模型进行拟合输出并与传统GM(1,1)模型和未优化背景值的FOTP-GM(1,1)模型比较预测精度的变化情况。 以齐次指数序列、带常数项的非齐次指数序列、带速度项、常数项的非齐次指数序列和带加速度项、速度项和常数项的非齐次指数数列为例,分别进行背景值的粒子群算法优化。 结果表明,经过背景值优化后4 种不同类型数据序列模拟精度以及预测精度均得到提高,齐次指数序列、带常数项非齐次指数序列预测精度提升最为明显,背景值优化后平均相对百分误差只有0.02%和1.48%,带加速度项、速度项、常数项的非齐次指数序列预测精度也得到了提升。 所以,FOTP-GM(1,1)模型本身可以适用于上述4 种数据类型,而这种将固定参数转变为一定范围内的动态值利用粒子群算法进行寻优,可以实现预测精度的显著提升,也为相关灰色预测模型的改进优化提供了思路和研究方向。

