基于NGO－VMD－FCBF－Informer 的电力负荷组合预测模型

蒲 维，杨毅强，张渊博，付江涛，宋 弘

（1 四川轻化工大学自动化与信息工程学院，四川 宜宾 644000； 2 人工智能四川省重点实验室，四川 宜宾 644000； 3 阿坝师范学院，四川 阿坝 623002）

0 引 言

在国内发布“十四五”的规划中，明确指出加快电网基础设施智能化改造和智能微电网建设，提高电力系统互补互济和智能调节能力将成为未来的发展方向。 电力资源作为一种二次能源，是其他各行各业健康发展的基石，高精准的电力负荷预测对整个电力系统经济有效、安全运行起着不容忽视的作用［1］。 随着新能源汽车等用电设备的数量不断增长，导致电网的随机性、不确定性、不稳定性进一步提高，因此，迫切需要一种稳定性好、预测精度高的电力负荷预测模型。

文献［2－3］分别采用了粒子群算法和遗传算法进行参数优化，虽然对预测精度有所提升，但这2 种算法存在收敛速度缓慢，且复杂繁琐的问题。 文献［4－5］采用了经验模态分解对原始数据进行分解，但在使用经验模态分解的过程中会伴随有端点效应、模态混叠等情况，而变分模态分解可以有效地避免经验模态分解存在的问题［6－9］。 文献［10－12］中选用单一的电力负荷数据作为输入特征，未考虑到影响负荷数据的其他因素（如工作日、温度、电价），不能充分提取变量间的信息关系。 文献［13－14］中采用循环神经网络（Recurrent Neural Network，RNN）进行预测，该网络能够很好地捕获数据的时序性，但经常伴随着梯度消失、爆炸的问题。 文献［1，3，11，15］中采用长短期记忆神经网络（Long Short－Term Memory，LSTM）。 LSTM 网络是在RNN基础上添加多个阈值门改进的，能够很好地解决RNN 网络梯度消失、爆炸的问题，但当原始数据呈现高度线性，且含有噪声时，采用LSTM 网络进行预测模型训练会导致过拟合的情况。 文献［9，16］中，采用了BP 神经网络（Back propagation，BP）进行训练，其权值和阈值等参数在训练过程中是随机产生的，且BP 网络存在学习率低，泛化能力弱，同时极易陷入局部最优的问题［17］。

基于已有的研究内容，本文提出了一种新型的预测模型—基于NGO－VMD－FCBF－Informer 电力负荷组合预测模型，以解决现有电力负荷预测模型优化方法不够理想的问题，同时对该模型进行了有效性的论证。

1 算法原理

1.1 北方苍鹰优化算法

Dehghani 等学者［18］在研究北方苍鹰捕食行为的过程中获得了灵感，由此提出了一种新的搜索算法，并将其命名为北方苍鹰优化算法（Northern Goshawk Optimization，NGO）。 该优化算法主要是对北方苍鹰的捕食行为进行模拟，北方苍鹰种群作为NGO 算法中的搜索者，种群中每只北方苍鹰需要对目标猎物的捕获问题提出解决方案，NGO 算法的优化效果明显强于GWO 算法、WOA 算法及MPA算法［18］。

捕食过程由猎物识别和猎物捕获两个阶段组成。 在猎物识别阶段中，北方苍鹰进行全局随机搜索，识别并选择最佳区域猎物，同时发动快速攻击。表达式如下：

其中，Pi为第i只北方苍鹰的目标猎物位置；Xk为K只北方苍鹰向量组成的矩阵；为新状态第一阶段下第i个提议的解决方案的第j个维度。为第一阶段的目标函数值；r为［0，1］ 区间的随机数；I也是随机数，其值可以取1 或2。

在猎物捕获阶段中，由于猎物试图逃跑，因此存在一个短暂的追逐过程——追尾，然后捕获猎物。这种行为的模拟增加了算法对搜索空间的局部搜索的利用能力。 表达式如下：

其中，R为种群攻击范围半径；t为当前迭代次数；T为最大迭代次数；为第二阶段的目标函数值。

1.2 变分模态分解

变分模态分解（Variational Mode Decomposition，VMD）算法是由Dragomiretskiy 等学者［19］在2014年提出了一种新型完全非递归的模态信号处理方法。该方法可以通过特定的方式将原始数据分解成若干个不同带宽及频率的本征模态函数（Intrinsic Mode Function，IMF）。

与经验模态分解相比，VMD 分解可以有效的避免端点效应及模态混叠的情况，可以更好地提取负荷数据信息，并且，VMD 分解的IMF 分量层数K及惩罚因子α 可以人为设置，其自适应性明显更强。针对电力负荷数据具有非线性、非平稳性等特点，VMD 分解是一种非常适宜的分解方法。

1.3 快速相关性滤波算法

快速相关性滤波算法（Fast Correlation－Based Filter，FCBF）作为一种典型基于相关性分析的特征选择方法之一，能有效衡量2 个特征变量之间相关性，其评判标准为对称不确定性（Symmetrical Uncertainty，SU），以此筛选出与目标特征变量相关性高的特征变量［20］。

在相关信息量中引入熵作为随机特征X与Y不确定性的度量，通过熵的定义可以将特征X的熵进行表达，则可进一步表达出同时满足特征X与Y的条件熵。 表达式如下：

其中，P（xi）、P（yj）分别表示当随机特征X与Y取xi、yj值的概率。

引入信息增益（Information Gain，IG） 来表达在特征X熵减（Y提供的关于X的额外信息），表达式如下：

可得出SU的表达式：

其中，SU的取值范围为（0，1），且值越大表示2个特征变量之间相关性程度越高。

1.4 Informer 模型

研究表明，Transformer 在提高预测精准度方面具有潜力，但Transformer 存在二次时间复杂度、高内存使用量和编码器－解码器体系结构固有的局限性等问题。 为了解决这些问题，Informer 模型应运而生［21］，该模型对Transformer 原有的自注意力机制进行了概率稀疏化，降低了计算复杂度，并有效提高了序列预测的准确度［22］。 Informer 模型结构如图1所示。

图1 Informer 模型结构图Fig. 1 Informer model structure diagram

1.4.1 稀疏自注意力机制

与传统的自注意力机制相比，稀疏自注意力机制在将传统的自注意力机制的Q（Query）进行稀疏化操作得到新的。 稀疏自注意力机制的公式如下：

其中，A表示Attention机制；Q，K，V表示由输入变量线性变换获得的相同行列的3 个矩阵；T表示矩阵的转置；softmax表示激活函数；d表示变量输入维度。

1.4.2 编码器

编码器（Encoder）由数量若干的多头概率稀疏自注意力和“蒸馏”（Distilling）共同构成，是用来接受输入端长时间序列数据输入，同时从输入中获取数据的长期依赖性。 自注意力蒸馏机制公式如下：

1.4.3 解码器

解码器（Decoder）由一个多头自注意力和一个掩码多头稀疏自注意力共同构成，采用生成式预测方式来缓解长序列预测时的速度过慢的问题。 公式如下：

其中，表示start token；L为时间序列的长度。

2 基于NGO－VMD－FCBF－Informer 的电力负荷组合预测模型

2.1 实验数据

2.1.1 数据选取

本文选取某地2010年7月至9月期间电力负荷数据集，其负荷数据信息采样间隔为30 min，采集共计4 415 组负荷数据。 在此，选取2010年7月1日至9月20日，共计3 936 组数据作为训练集，选取2010年9月21日至30日，共计479 组数据作为测试集。

该数据集包含了7 个实时特征变量及电力负荷信息，其中包括2 个时间序列特征变量：时间点与星期变量；4 个气象特征变量：干球温度、露点温度、湿球温度及湿度变量；1 个市场特征变量：电价变量。

2.1.2 数据预处理

由于原始数据的输入特征变量在数值上可能存在相差几个量级的问题，这将导致数量级大的特征变量在学习算法中占据主导地位，从而忽略了针对量级小的特征变量的学习。 为了解决量纲上存在差距造成的影响，同时提高算法的收敛速度及预测精度的问题，本文选用Min－Max 归一化对负荷数据进行归一化处理。 归一化公式如下：

其中，Xmax和Xmin分别为原始数据中的最大值及最小值；X′为归一化处理后的数据值。

2.1.3 性能评价指标

本文选用了均值绝对误差（MAE）、平均绝对百分比误差（MAPE） 及均方根误差（RMSE） 三个指标作为实验负荷预测结果精度的衡量标准。 性能评价指标的数值越低，表明该模型的预测精度越精准。性能评价指标的公式如下：

其中，hp、hi分别表示t ＝i的预测值和实际值。

2.2 基于NGO－VMD－FCBF－Informer 的电力负荷组合预测模型流程

基于NGO－VMD－FCBF－Informer 的电力负荷组合预测模型流程如图2 所示。 整个预测流程由2 个部分共同组成：NGO 算法优化VMD 分解部分及FCBF－Informer 电力负荷预测部分。

图2 NGO－VMD－FCBF－Informer 组合预测模型流程图Fig. 2 Flow chart of NGO－VMD－FCBF－Informer combination prediction model

2.2.1 NGO－VMD（OVMD）

在使用VMD 分解对原始数据进行处理前，需要手动设置IMF分量层数K及惩罚因子α。 由于这2 个参数在VMD 分解中占据着主导地位，对分解的结果起着决定性的作用，如若参数设置不当将导致后续步骤难以进行［22］。 纵然研究人员可以凭借经验对2 个参数进行预先设置，但人为设置参数会存在主观性、随机性等问题。 且参数往往需要多次设置、直至较优，该过程繁琐且费时费力，并且人为确定的最终参数极大可能会逊于NGO 算法寻优确定的参数，这将导致VMD 分解不充分，原始数据的非线性、非平稳性不能得到最大程度的缓解。 因此，本文选用NGO 算法对VMD 分解的IMF分量层数K及惩罚因子α进行寻优，OVMD 部分的主要工作是对原始数据进行分解处理。 采用NGO 算法优化VMD 分解的［K，α］ 参数组合具体步骤如下。

（1）设置VMD 分解的收敛容差等基本参数。

（2）设置NGO 算法的种群数及最大迭代次数；选用样本熵局部最小值作为NGO 算法适应度函数。

（3）设置VMD 分解的［K，α］ 参数组合寻优范围。

（4）利用VMD 对原始信号进行分解处理，同时计算出寻优范围内不同［K，α］ 参数组合的适应度值。

（5）随着迭代的进行，利用NGO 算法的优化机制不断更新出种群个体的位置信息。

（6）循环（4） ～（5）的步骤，直至获得了最优［K，α］ 参数组合或者迭代次数达到预设最大迭代次数。

（7）输出当前最优［K，α］ 参数组合。

本文设置IMF分量个数k及惩罚因子α的寻优范围分别为［2，20］与［200，4 000］，［k，α］ 参数组合经过NGO 算法寻优，最终本文确定的最优［k，α］参数组合为［18，3 400］，利用VMD 算法对原始数据进行分解。 根据分解的结果可知，IMF1 分量至IMF18 分量的分量频率依次增大，数值量级依次减小。 在这18 个IMF分量中，IMF1 所占数量级最大、且与原始数据最为接近，IMF2 分量与IMF3 分量的数值量级属于同级，IMF4 分量至IMF18 分量的数值量级较一致。

2.2.2 FCBF－Informer

FCBF－Informer 的作用是筛选出与电力负荷高度相关的特征变量作为输入变量后进行负荷预测，采用FCBF－Informer 进行负荷预测的具体步骤如下：

（1） 在经过NGO 算法对VMD 分解的IMF分量层数K及惩罚因子α的优化步骤后，采用FCBF算法对多维特征变量进行筛选，筛选出与电力负荷高度相关的特征变量作为输入变量。

（2） 将确定作为输入变量的特征变量与各个IMF分量同时作为Informer 模型的输入，对输入变量进行归一化处理后，再进行训练和预测，得到各个IMF分量对应的预测值。

（3）对各个IMF分量的预测值进行反归一化操作，将反归一化操作后各个IMF分量预测值进行重构叠加得到最终的预测值，并将该值与原始数据进行对比分析。

经过FCBF 算法的处理，可以获知，本文选用数据集的原始输入特征变量与电力负荷相关程度由高到低依次为电价、露点温度、干球温度、湿球温度、湿度以及星期（未计入时间点特征变量），并且星期特征变量相关性较小，所以本文选择除去星期特征变量剩余的5 个特征变量作为Informer 模型的输入变量。

3 算例分析

3.1 Informer 模型超参数确定

在Informer 模型中，不同的超参数会对负荷预测的精度产生重大的影响。 经过多次实验本文最终确定Informer 模型的编码器、解码器的输入步长及层数等基本超参数设置，见表1。

表1 Informer 模型超参数设置Tab. 1 Setting of Informer model hyperparameters

3.2 实验结果

3.2.1 组合模型实验结果

为论证OVMD 及FCBF 算法引入到Informer 模型的可行性和有效性，在此将OVMD、FCBF 与Informer 进行了组合，构成不同组合预测模型进行预测。 性能指标见表2，实验结果如图3 所示。

表2 不同组合模型的性能评价指标Tab. 2 Performance evaluation indexes of different combination models

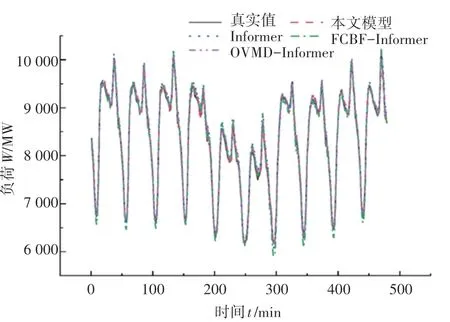
图3 不同组合预测模型结果Fig. 3 Results of different combination prediction models

FCBF－Informer 及OVMD－Informer 两种模型在3 个性能评价指标上均有不同程度上的降低。 在Informer 模型中引入FCBF 算法，FCBF 算法可以在众多特征变量中筛选出与预测变量相关性较大的特征变量，研究人员可以自主地选择输入特征变量，避免了特征变量间的冗余，在降低计算时间的同时，提高了收敛速度。 Informer 模型中引入OVMD 分解，OVMD 分解可以降低原始数据的非线性、非平稳性，减少了波峰和波谷的出现次数，提高原始数据的质量。

同时，相比于 Informer、 FCBF － Informer 及OVMD－Informer 三种模型，本文模型进一步降代了3 个性能评价指标，本文模型预测结果的性能评价指标MAE为 48.21，MAPE为 0.58%，RMSE为59.48。 该模型预测曲线拟合程度在一定程度上得到加强，尤其是在预测波峰和波谷到来的时间点，其预测结果与真实值更为接近。 充分论证了在Informer 模型基础上引入OVMD 分解及FCBF 算法的可行性和有效性。

3.2.2 不同模型实验结果

为了进一步论证本文模型的可行性和有效性，在此选用了BP、LSTM、CNN－LSTM、CNN－BiLSTM等模型与本文模型进行了对比实验。 为了保障实验的客观性，对比实验模型中超参数的设置尽量与本文模型保持相同或者一致（如输入步长、丢弃率、批量大小等），若对比模型中存在本文模型没有的超参数，而其他模型拥有同类超参数也应该相同或者一致（如隐藏层的层数、神经元个数等）。 性能指标见表3，实验结果如图4 所示。

表3 不同模型的性能评价指标Tab. 3 Performance evaluation indexes of different models

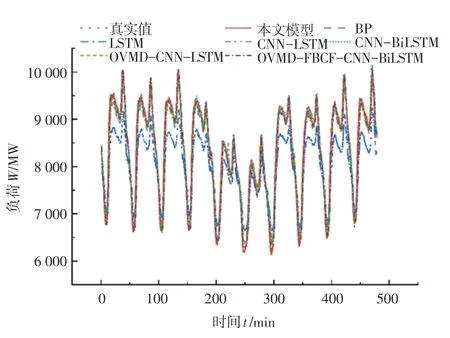
图4 不同模型预测结果Fig. 4 Different models predict results

由所列不同模型的性能评价指标可知，与BP、LSTM、CNN－LSTM、CNN－BiLSTM 这类单一预测模型相比，Informer 模型有着不错的预测效果，这是因其在时域上对非平稳性、非线性负荷数据拥有更为敏感的感知能力，同时在捕捉历史负荷数据输入特征变量及特征变量间的潜在信息更为充分，能够对输入输出之间进行更为高效的拟合，因而该模型的预测性能更为优异。 不过，单一的预测模型对历史负荷数据集质量要求苛刻，在对非平稳性、非线性的历史负荷数据进行预测时得到的结果精度较差。

组合模型可以在保障历史负荷数据的时序性基础上提高其平稳性，同时对输入特征变量进行筛选，进行多变量对单变量的负荷预测。 由此可见，组合模型预测相比单一预测模型有着更为满意的结果。

4 结束语

为了解决现有预测模型优化方法不够理想、预测精度不高的问题，本文提出了一种基于NGOVMD－FCBF－Informer 的电力负荷组合预测模型，经过仿真对比实验论证，得出了如下结论：

（1）文中利用NGO 算法对VMD 分解的IMF 分量层数K及惩罚因子α寻优，经过OVMD 处理后的数据相较于原始数据，在很大程度上其非线性、非平稳性得以降低，有利于Informer 模型更好地进行训练。

（2）文中考虑了气象条件等影响因素，同时采用FCBF 算法对影响负荷的特征变量进行筛选作为预测模型输入，不仅可以减少部分工作量，加快算法的计算速度，同时对预测模型的精度有一定的改善。

（3）根据实验结果显示，本文提出的预测模型克服了单一模型的局限性，有效地解决了现有方法预测结果精度不高的问题，可以为电力系统的日常工作、安排提供有益的理论指导参考，具有极其重要的意义。