融合指标分组的高维混合多目标进化优化

李 玲，郭广颂

郑州航空工业管理学院 智能工程学院，郑州 450046

在实际优化问题中，存在很多同时包含显式指标（定量指标）和隐式指标（定性指标）的优化类型，如光栅优化[1]、钢梁设计[2]、柴油机标定[3]、机场故障处理[4]等，这类问题称为混合指标优化问题。当混合指标优化问题包含4个及以上目标时，该问题称为高维混合多目标优化问题。尽管近年来提出并得到迅速发展的NSGA-II、SPEA2、MOEA等多目标进化优化方法可以有效解决传统的多目标优化问题，但是对于高维混合多目标优化问题，上述方法难以得到问题的Pareto最优解。主要原因在于，种群中非被占优解的比率会随着目标个数的增加而急剧增长，使得Pareto 占优准则无法区分个体性能，这就导致基于密度估计方法的选择标准成为主导。然而，由于这些算法的密度估计方法无法在高维目标空间中恰当评估个体性能，结果保留了大量远离Pareto前沿的占优抵抗解。特别地，当优化指标为混合指标时，因隐式指标无法用目标函数表示，极大地增加了问题的求解难度。

目前主要有三种途径求解高维混合多目标优化问题：（1）考虑优化目标的多样性与复杂性，采用启发式算法或智能算法对所有目标同时进行Pareto 优化[5-6]。启发式算法和智能算法在这一研究中表现出巨大潜力，这也是目前求解高维混合多目标优化问题的主要研究途径。但同时对所有目标进行Pareto占优求解，算法计算开销巨大，收敛性和多样性较差。（2）采用协同进化优化，缩小子种群搜索空间，提高算法搜索效率[7-8]。协同进化优化方法很适合大规模多目标优化问题求解，但对混合指标优化中两类指标的协调问题尚缺乏有效策略。（3）采用交互式进化优化，将混合多目标问题转化为确定性多目标或单目标问题[9-11]。该类方法对一维或二维混合指标问题效果较好，对于高维混合指标问题优化效果较差。

由于高维混合多目标优化问题的两类指标性质不同，按传统多目标优化思路对混合指标加权转化成确定性多目标或单目标问题求解，难以确定目标权重。另外，对于隐式指标的评价，无论由人直接完成，还是由代理模型完成，相比显式指标运算速度都要慢很多。两类指标进化速度的不一致，会严重影响进化优化效率和Pareto最优解质量。文献[12]将高维多目标优化问题分解为若干子优化问题，采用多种群并行进化求解每一子优化问题。结合高维混合多目标特点，如果根据指标性质对混合指标分组，采用并行进化优化，每个子种群只优化少量单纯显式指标或隐式指标，并基于聚合函数对子种群Pareto解进一步优化，则可以利用多种群并行运算快速获得整体最优Pareto解。实现这一思想，需要足够多满足多样性与覆盖性的样本，并对隐式指标做出准确的估计。

鉴于此，本文提出一种基于指标分组的高维混合多目标并行进化优化方法。主要思想是：基于人评价的少样本个体隐式指标，采用深度卷积神经网络实现大规模种群隐式指标预测；按指标相关性，分别对显式指标和隐式指标分组，形成若干子优化问题；采用多种群并行进化算法求解各子优化问题，并将各子种群的优化解组成外部保存集；采用聚合函数对外部保存集的优化解进一步优化，获得优化问题的Pareto最优解。

本文方法的创新之处是：（1）将两类指标单独转化成若干个目标函数较少的多目标优化问题，采用子种群并行进化优化求解，提高了问题求解速度；（2）并行进化过程中，在隐式指标预测的同时，允许显式指标完成多次进化，提高了显式指标优化进程，缩小了用户对隐式指标评价次数；（3）采用深度学习神经网络预测隐式指标，实现大规模种群评价，指标评价更准确，减轻了用户疲劳；（4）采用外部保存集对聚合函数进一步优化，保证了Pareto最优解的逼近性与分布性。

1 相关工作

1.1 混合指标进化优化

混合指标优化问题是多目标优化问题的特殊类型，显式指标与隐式指标并存是这类问题的显著特征。相比单纯数值多目标优化，该问题研究较少，且研究方法主要沿用传统多目标优化策略。现有研究成果中，一类集中于将混合指标优化问题转化为确定型多目标优化问题。这类方法大多采用在搜索过程中融入用户决策的交互式优化方法，因为通过人机交互，用户可以对优化结果的性能指标做出更合理的判断[13]。Satoshi 等将定性与定量指标加权转化为一个适应值函数，采用交互式进化计算进行图像处理滤波器设计[14]；Garcia-Hernandez等将用户评价的隐式指标与显式指标合成为一个适应值，采用交互式进化优化方法求解不等面积设施布局问题（unequal area facility layout problem，UA-FLP）[15]。另一类研究集中于改进进化策略提高算法性能，或是与第一类情况的混合。Liu等基于启发式变异操作和后续配置一个考虑梯度方法的局部搜索策略，提高算法效率[16]；Liu提出了一种多目标蚁群优化算法解决UA-FLP中物料搬运成本和距离要求，该方法通过启发式技术将约束问题转化为无约束问题，然后应用局部搜索、Pareto优化、设施变形和小生境等策略达到有效的设施设计[17]；García-Hernández等提出了一种支持用户定性标准的多目标交互式遗传算法[18]。由于含有隐式指标，对于相同的混合指标优化问题，采用不同的转化方法，得到的确定优化问题是不同的，相应地，这些确定优化问题的解也可能不同。这意味着，不同的转化方法会得到混合指标优化问题的不同解，那么决策者如何从这些解中进一步选择是一个很困难的问题。特别地，上述方法的研究对象均为1个隐式指标与1个或2个显式指标的混合情况，没有涉及高维混合目标的优化问题。

1.2 协同进化优化

协同进化优化算法（cooperative co-evolutionary algorithm，CCEA）是一种将多变量优化问题分解为若干简单少变量的子优化问题，将种群划分为若干个与子优化问题对应的子种群的优化方法。该方法通过构建每个子种群的搜索结果构成问题的完整解，进而得到问题的最优解。相对于单目标优化问题，利用协同进化优化算法求解多目标优化问题，目前的研究成果较少。Ma等提出一种基于决策变量分析的多目标进化算法，并使用控制变量分析来识别目标函数之间的冲突[19]；Li等建立了一个协同搜索框架用于对3个目标特征的选择，以此克服建模选择优化特征子集过程中保持分类精度和减少特征数量的矛盾[20]；另外，Tirumala通过2 个子种群协同进化优化深度学习网络，为深度学习与进化优化结合提供了新思路[21]。最近，协同进化优化算法还被用于动态多目标优化问题[22-23]。上述方法为求解多目标优化问题提供了可行途径。然而，由于缺少预测隐式指标方法及与显式指标协调的目标函数构建策略，现有协同进化优化算法无法直接用于求解高维混合多目标优化问题。

2 提出的方法

2.1 优化问题

考虑如下一类高维混合多目标优化问题：

式中，x为n维决策变量；S为x的可行域；fi(x,ci)(i=1,2,…,p)为含参数ci的显式性能指标对应的目标函数；为隐式性能指标，是用户对进化个体满足程度的定性评价值。

2.2 总体框架

本文提出一种高维混合多目标并行进化优化方法求解问题（1），总体框架如图1所示。首先，将高维混合多目标优化问题按显式指标与隐式指标两类目标分组，原优化问题被分成规模较小的K个显式指标和K′个隐式指标子优化问题；其次，按对子优化问题的相关性，将种群分成K+K′个子种群；然后，每个子种群对应优化一个子问题，这一过程融入小样本深度学习预测隐式性能指标，通过子种群并行进化提高种群多样性；最后，将各子种群的Pareto最优解集合并成外部保存集，通过优化聚合函数实现聚合优化，获得逼近性最佳解集，再从中选择出代表性个体推荐给用户评价，完成一次迭代。

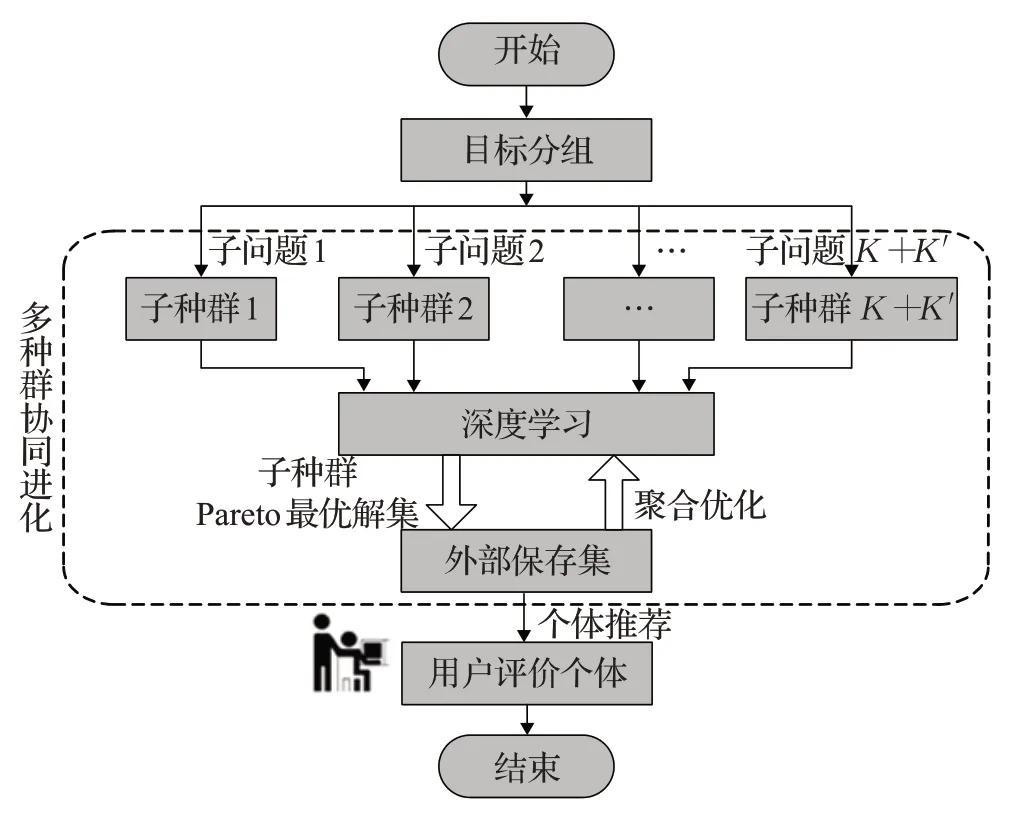
图1 算法框架Fig.1 Algorithm framework

可以看出，目标分组、子优化问题进化求解、外部保存集的形成与更新是本文方法的关键技术。

2.3 目标分组

问题（1）包含显式指标与隐式指标两类指标，不仅指标数量较多，而且指标还可能是冲突的，直接作为优化目标很难获得Pareto最优解。基于此，本节根据相关性对问题（1）进行目标分组。具体方法是：每一进化代对种群所有个体，计算显式指标目标函数fa(x,c) 与fb(x,c)之间的Spearma 相关系数ρa,b,a,b=1,2,…,p,如果ρa,b超过阈值，则fa(x,c)与fb(x,c)可以分为一组，记为。由于隐式指标没有目标函数，则计算每一进化代种群所有个体隐式指标值的Pearson 相关系数ra′,b′,a′,b′=p+1,p+2,…,p+q,如果ra′,b′超过阈值，则可以分为一组，记为。对于最后没有匹配的剩余隐式指标，则单独归为一组。根据上述分组方法，问题（1）描述的高维混合多目标优化问题可以分成如下K+K′组：

式中，fkh(x,c),k=1,2,…,K,h=1,2,…,mk，是组Gk包含的第h个显式指标目标函数；,k′=p+1,p+2,…,p+K′,h′=1,2,…,mk′是组Gk+k′包含的第h′个隐式指标目标函数，且满足K+K′≤p+q。

式（2）的分组结果体现出将问题（1）两类指标中最相关的目标划为一类，其中K由优化问题（1）的显式目标函数性质决定，K′则由隐式指标结果和数量决定。按式（2）可将问题（1）的1 个优化问题分成如下K+K′个子优化问题：

与问题（1）相比，式（3）子优化问题的优化目标个数明显减少，因此问题复杂性降低，更容易求解Pareto解。

2.4 子优化问题的并行进化求解

对于问题（3），本节采用子种群并行进化求解，通过多种群并行进化实现高效求解问题（1），具体分为如下三个阶段。

（1）深度学习

受疲劳限制，人评价个体数量有限，基于此，本节采用深度神经网络的少样本学习方法实现大规模种群个体的隐式指标赋值。记第t代进化种群为x(t)，种群规模为N，供用户评价的推荐个体为xc(t),c=1,2,…,Nc，则种群剩余个体记为xre(t),re=1,2,…,N-Nc。将上一代种群DL(t-1)={(xi(t-1),f(xi(t-1)))|i=1,2,…,N}作为初始样本训练集，Dl(t)={(xc(t),f(xc(t)))|c=1,2,…,Nc}作为小样本训练集，xre(t)的隐式指标通过学习获得。深度学习部分基于深度卷积神经网络构建。深度学习的初始训练部分，将DL(t-1)的个体{xi(t-1)}以图片形式作为输入，直接采用深度神经网络卷积1 提取个体{xi(t-1)} 的属性特征，再将属性向量输入两层全连接层训练，得到个体特征。设个体属性特征向量为d′，使用卷积核对d′学习，经过池化层，得到个体特征向量：

对于xi(t-1)的评价值f(xi(t-1))，采用嵌入层处理，获得个体隐式指标向量。将和个体隐式指标向量一并通过两层全连接层训练，得到偏好特征。

采用小样本训练集Dl(t)对上述分类器按平方梯度幅度损失（squared gradient magnitude loss，SGM）进行微调，实现小样本学习[24]。Dl(t)的个体{xc(t)}以图片形式作为输入，采用卷积2提取个体属性特征，按式（4）得到个体特征向量。对于推荐个体xc(t)的评价值f(xc(t))，也采用嵌入层处理，获得个体隐式指标向量。将和个体隐式指标向量一并通过两层全连接层训练，得到偏好特征。同理，测试集{xre(t)}采用卷积1和全连接层训练，得到种群剩余个体特征。将和输入到全连接层，采用Adams算法作为优化策略[25]，进行特征匹配。对输出值进行Logistic Regression，得出剩余个体xre(t)的隐式指标预测概率值：

（2）子种群划分

为了提高优化效率，采用子种群并行优化策略。即要求子种群对应求解问题（3）的子优化问题，这需要各子种群内个体的指标分布应与所优化目标一致。基于此，采用个体指标均衡度划分子种群[26]。在交互式进化过程中，由于每一代的个体指标在决策中所起作用相同，设指标效用系数为1，且每一代均能收集到相关数据对相应指标进行评价，故直接将个体xi(t)的显式指标与隐式指标分别归一化，再做升序排列，记为V11(xi(t)),V12(xi(t)),…,V1p(xi(t));V1p+1(xi(t)),V1p+2(xi(t)),…,V1(p+q)(xi(t)),则个体xi(t),i=1,2,…,N的指标均衡度为：

其中Gip(t),Giq(t)∈[0,1],Gip(t)、Giq(t)可以反映两类性能指标的动态差异性，Gip(t)、Giq(t)越大，表明个体的两类指标分布越均衡，反之，两类指标分布差异越大。

采用式（7），对种群个体分别计算式（2）的目标分组指标均衡度。在两类指标均衡度中，每次选择一个指标均衡度最高的个体，共选择K+K′个个体。以这K+K′个个体为中心，按基因相似性对种群聚类，则种群可以分成K+K′个子种群。这些子种群的规模并不相同，但由于按目标分组指标均衡度划分聚类，Pareto最优解的选择压力更大，每一个子种群的个体分布更有利于求解子优化问题。

（3）子种群优化

从（2）中获得K+K′个子种群，采用并行优化方法，让每一个子种群采用NSGA-II 对应求解一个子优化问题。因为每一个子优化问题包含的目标数量较少，所以对于每一个子种群采用Pareto 占优关系比较个体性能。采用多种群并行优化的优势在于，由于不同子种群优化的目标不同，各子种群的进化方向也不同，这有利于保持整个进化种群的多样性。需要说明的是，由于大量隐式指标需要深度学习获得，这会造成子优化问题的优化速度比要慢很多。为了协调进化速度，子优化问 题每完成一次进化，允许完成多次进化，这样通过尽快优化显式指标提高进化速度，减少用户评价隐式指标的次数。

2.5 外部保存集的形成

第2.4 节（3）中子种群的Pareto 最优解代表了低维目标空间里子优化问题的最优解，这些最优解很可能是问题（1）的局部最优解，而非全局最优解。为了获得高维目标空间中，逼近性与分布性兼顾的Pareto 最优解，需要对子种群的Pareto最优解进一步选择。记第t代的外部保存集为，其中,k=1,2,…,K+K′表示来自第k个子种群的Pareto 最优解集，|At|≤N。因为外部保存集由组成，所以每代进化后，外部保存集中的个体将全部更新，其规模由决定。设聚合函数fK+K′(x)为：

式中，加撇的函数值是对原函数值归一化的结果。ωgh是显式指标目标函数fgh的权重，本文假设每个目标函数重要性相同，则ωgh=1/(p-mK)；ωqkh′是隐式指标的权重，同样认为每个隐式指标重要性相同，取ωqkh′=1/(p+q-mK′)。fK+K′(x)是所有子优化问题解与参考点之间的加权切比雪夫距离，优化解的fK+K′(x)值越小，到参考点距离越近，解的分布性越好，优化解性能也越好。通过At对fK+K′(x)的优化，可以平衡所有目标函数，获得具有好的逼近性能的最优解，记为Ct+1。这一聚合优化过程的可行解域At是子种群并行优化阶段的最优解域，由于优化目标只有fK+K′(x)，随着进化深入，At规模将不断缩小，优化问题复杂度也逐渐降低。聚合优化过程中，仍采用深度学习获得个体隐式指标。最后，按个体相似性，从Ct+1选择前Nc个个体推荐给用户，作为下一代评价个体。

3 实验

3.1 优化问题

对于混合指标优化，目前最广泛采用的测试问题是设施布局问题（facility layout problem，FLP）。本文采用属于FLP 的室内布局优化问题验证方法的性能[13]。室内布局方案由客厅、卧室等7个居室单元组成，如图2所示。布局总开间W和总进深H分别为W=12.5 m，H=10 m。该问题包含2个显式指标f1(x,c),f2(x,c)和2个隐式指标。其中，f1(x,c)是室内面积总造价（单位：元），f1(x,c)由决策变量x=[x1,x2,x3,x4,x5,x6,x7]和参数c=[c1,c2,c3,c4,c5,c6,c7]组成，决策变量x1～x7代表各居室单元的边长，x1,x4,x5,x6∈(0,10)，x2,x3,x7∈(0,12.5)，各变量均采用离散值，取值个数分别为5、12、5、5、5、5、5。将所有变量采用实数编码排列，构成个体基因型。参数c1～c7代表各居室单元的单位面积造价，c1=800,c2=1 000,c3=600,c4=1 000,c5=600,c6=600,c7=500。

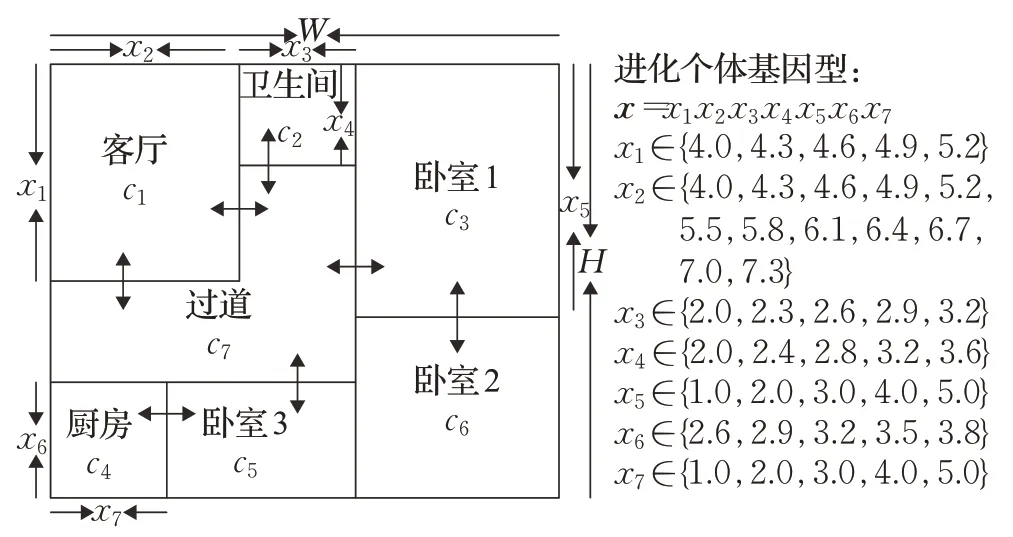
图2 室内布局Fig.2 Indoor layout

f2(x,c)是公摊面积与墙体面积和（单位：m2），其参数是公摊系数c8和墙体系数c9：

采用Google TensorFlow深度学习库开发进化优化系统。用户对每代12个推荐个体，在1～100整数范围内评价该个体的2个隐式指标，同时系统计算并显示每个个体的2个显式指标。在人机交互过程中，系统在后台运行相关算法，通过边交互边优化形式，逐渐生成用户满意的室内布局方案。

3.2 性能指标

因为隐式指标不能用目标函数表达，所以问题（1）的真实Pareto前沿面是不确定的，这导致传统多目标优化问题的世代距离（generation distance，GD）、反世代距离（inverted generation distance，IGD）等性能指标均不适用问题（1）。基于此，本文采用空间评价指标（spacing，SP）[27]和最大传播距离（maximum spread，MS）[28]评价解集的分布性和延展性，SP 值越小，解集的分布性越好，MS 值越大，解集的延展性越好；采用最好超体积（best hypervolume，bH）评估解集的逼近性[13]，bH 值越大，解集的逼近性越好；采用显式指标均值（E测度）和隐式指标均值（I测度）评价解集质量；采用迷失度[29]、满意性和进化耗时Tt等评价不同方法的可用性，Tt由机器耗时Tp和用户耗时Tu组成，Tp包含深度学习时间Tcn和并行程序运行时间Tnp。

3.3 对比方法及参数设置

采用本文方法和K均值聚类预测隐式指标开发的混合指标优化算法（记为方法1）、采用本文方法但不采用目标分组子种群并行进化开发的混合指标优化算法（记为方法2）和文献[13]提出的混合指标IGA（记为方法3）3种相关算法作为对比方法。这3种方法从不同角度求解混合指标优化问题，具有较强的代表性。

为验证算法有效性，分别按上述3种方法开发相应系统。方法参数设置相同，即种群规模N=500，用户评价个体数Nc=12，单点交叉概率pc=0.95，单点变异概率pm=0.01，最大进化代数T=10。对于单点交叉操作，父代个体交换随机选择的一个交叉点之后的编码串构成新个体；对于单点变异操作，从随机选择的一个变异点的基因对应的离散集合中，随机选择一个值代替该变异点的基因，产生新个体。选择男女各5名在校大学生作为体验用户，分别记为用户1～10。每位用户独立运行对比方法10 次，独立运行本文方法20 次，其中10次运行结果用于分析不同参数或策略对本文方法性能影响，另外10 次运行结果用于与对比方法比较分析本文方法的性能。

3.4 结果分析

3.4.1 不同参数或策略对本文方法性能影响

（1）目标分组方法

目标分组数K+K′是本文求解问题（1）的关键参数，分组数决定了问题（1）的子优化问题规模，直接影响优化结果。设Spearman 相关阈值与Pearson 相关阈值分别为。依据第2.3节，通过可以确定出K+K′。为了比较不同目标分组结果对优化性能的影响，本节设定不同，并确定出相应K+K′，通过性能指标比较算法性能，实验结果如表1所示。表中括号外的数据表示均值，括号内的数据为标准差，E测度和I测度分别包括2个显式指标测度E-1、E-2和2 个隐式指标测度I-1、I-2，粗体显示的数据是所有K+K′分组方法得到的最优结果。

表1 目标分组对性能的影响Table 1 Effects of indexs decomposition on performance

（2）深度学习预测隐式性能指标

根据第2.4 节（1），首先将上一代种群x(t-1)，共500 个个体作为初始样本训练集DL(t-1)，训练深度学习网络初始模型，然后将当前代12 个用户评价个体作为小样本训练集Dl(t)，对初始模型进行修正，最后将当前种群剩余488个个体作为测试集{xre(t)}，利用修正后的深度学习模型，预测当前种群剩余个体xre(t)的隐式性能指标。式（5）中，超参数偏好模型权重和个体模型权重对隐式性能指标预测具有重要影响。偏好特征和种群剩余个体特征均为特征向量。

对于混合指标优化问题，隐式指标预测最能体现算法的适应能力，因此采用隐式指标优化损失验证本文算法的泛化性：

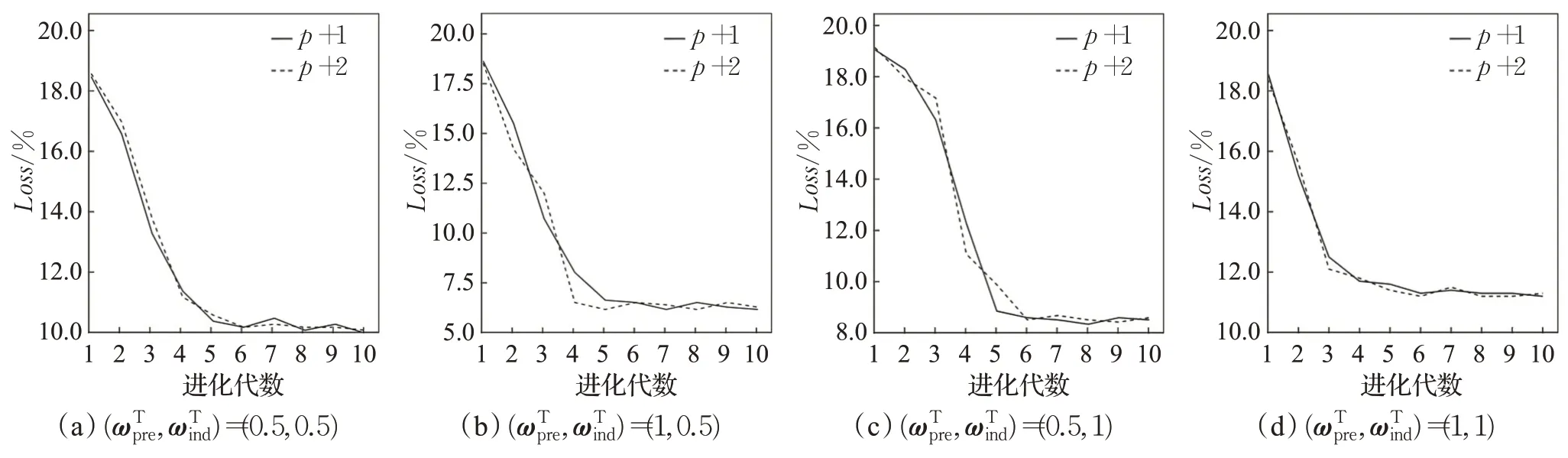
图3 深度学习神经网络Loss曲线Fig.3 Loss curves of deep learning neural network

（3）子种群并行进化

子种群并行进化是本文求解问题（1）的关键。子种群根据指标均衡度划分，不同的子种群划分决定了Pareto最优解数目。Tt和Tnp/Tcn可以反映两类指标协同进化效果。Tt越小，表明算法速度越快。Tnp/Tcn中，Tnp与Tcn越接近，表明在隐式指标深度学习预测的同时，显式指标进化次数越多，指标协调性越好。图4给出了指标分组数目K/K′的变化情况，可以看到，随着进化深入，K/K′逐渐趋于0.5，即K+K′=1+2。这说明，显式指标分组趋同，隐式指标分为2 组，本文方法的指标分组策略有效。表2 给出了10 位用户子种群并行进化统计结果，其中分别是Gip(t)和Giq(t)的均值。表中10位用户的均在0.8以上，且差异不显著，说明子种群并行进化可以获得良好的指标均衡性。10 位用户的分组结果中，K均为1，有4 位用户的K′为2，说明显式指标相关性一致，隐式指标相关性会因个性偏好产生差异。K′越小，最优解越多，可能的原因是将2个个性偏好蕴含相关的隐式指标独立优化，外部保存集中生成的非全局最优解较多，但对聚合函数的Pareto最优解较少。K′越大，Tt越大，原因在于对隐式指标优化的子种群数量增加，导致并行进化代数增加，耗时随之增加。10位用户的Tnp/Tcn差异不显著，说明虽然用户的目标分组不同，但是采用子种群并行优化的指标协调性是一致的，即能够通过尽快优化显式指标，减少用户评价隐式指标次数。

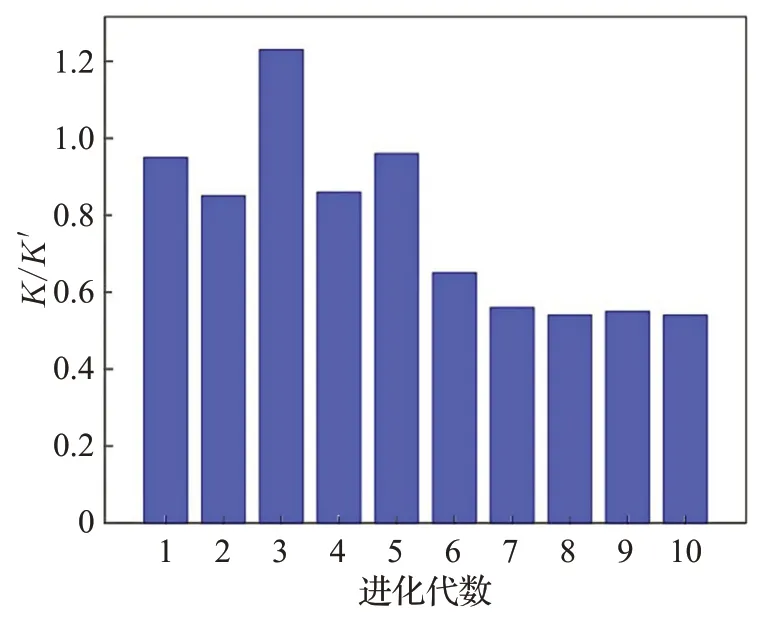
图4 指标分组比值Fig.4 Indexs decomposition ratio

表2 子种群并行进化对性能的影响Table 2 Effects of subpopulation parallel evolution on performance

3.4.2 与其他方法的对比

（1）指标均衡性

指标均衡性是指标分组的基础，考察进化过程中指标均衡性变化对于分析算法性能具有重要意义。本文方法与对比方法的种群指标均衡度如图5 所示。可以看到，本文方法的均高于对比方法，这表明采用本文方法，即便对于不同用户，问题（1）的显式指标和隐式指标均能获得最佳优化。原因在于，本文方法的指标分组策略提高了优化速度，各子种群可以获得更好的种群多样性。因为在隐式指标预测的同时，允许显式指标完成多次进化，提高了显式指标优化进程，所以本文方法的略高于。类似地，方法1的显式指标均衡度高于方法2和方法3。由图5（b）可见，对比方法中，相同进化代内变化比略大，这是因为隐式指标估计与聚类策略和指标分组策略密切相关，当用户评价个体选择不同时，深度学习的结果也将不同，这将导致隐式指标均衡性的改变。本文方法的隐式指标估计策略比对比方法全面，因此变化最小。基于良好的指标均衡性，为获得Pareto最优解提供了依据。

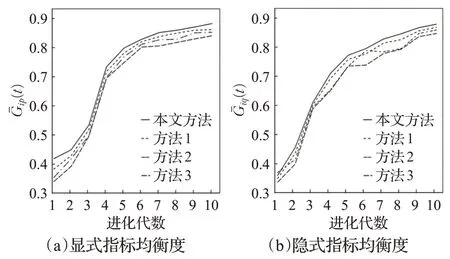
图5 指标均衡度Fig.5 Index equilibrium degree

（2）Pareto最优解集质量

比较本文方法和对比方法获得的Pareto最优解，对4种方法最优解指标取均值，统计结果如表3所示，其中粗体显示的数据为所有方法得到的最优结果。从表中可以看到，本文方法最优解数量最多，说明本文方法可以获得最多性价比高的布局方案，推荐用户评价个体更为丰富。4种方法中，本文方法SP最小，方法1比方法2和方法3的SP都小，说明本文方法的Pareto最优解分布性最好，原因在于本文方法和方法1均采用子种群并行进化，可以获得分布性更均匀的Pareto最优解。本文方法和方法1 均采用目标分组，因为本文方法多数用户K+K′为1+1，所以MS接近1，且大于方法1。方法2和方法3 均采用所有性能指标加权的单目标优化，所以MS均达到最大值。这表明本文方法采用深度学习预测隐式性能指标比方法2 更准确，Pareto 前沿延展性更好。本文方法bH 最大，说明本文方法获得的Pareto 前沿更接近真实Pareto前沿，原因在于本文方法的探索能力强，更有利于找到最优解。本文方法E 测度最小，说明本文方法获得的Pareto最优解造价最低，套内面积最大。本文方法I测度最大，说明即便10个用户存在偏好差异，本文方法获得的个体评价值仍最高。本文方法E测度最小，反映出本文方法针对存在偏好差异情况下获得的Pareto最优解性价比更高。

表3 Pareto最优解集质量Table 3 Quality of Pareto optimal solution set

（3）交互性

算法的交互性从可用性和推荐性两方面评价。征询用户对室内布局方案的定性评价意见，用户对室内布局方案的偏好概括如下：（1）客厅面积应最大；（2）卫生间面积应在5～8 m2之间；（3）3 个卧室中，卧室1（主卧）面积应最大；（4）厨房布局应对称；（5）卧室2和卧室3面积应接近；（6）过道不宜太狭窄。结合上述意见，构造评价结果满意性指标S(x)，如式（12）所示，S(x)值越小，相应个体就越满足上述评价意见，用户的满意程度也越高。需要说明的是，由于隐式指标评价强烈依据个性化偏好，式（12）不能充分地表达隐式评价指标，只能必要地衡量优化结果满意性，因此式（12）不能作为隐式指标函数代替参与优化。图6（a）给出了4 种方法的S(x)均值箱图，由图可见，本文方法的S(x)值最小。这表明本文方法优化结果更能体现用户偏好，算法对隐式指标的刻画能力最强。

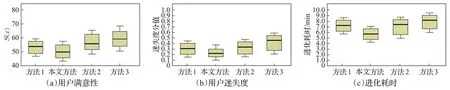
图6 可用性指标Fig.6 Availability indicators

迷失度用于度量用户对操作对象的迷茫程度，反映用户的疲劳性感受[29]：

式中，No′是用户在一次进化任务中评价的互异个体数目，No′是用户在一次进化任务中获得的最优评价的个体数目，T′是算法运行终止进化代数。当迷失度小于0.4 时，用户不会对操作对象显示出任何可观察到的迷失特征，当迷失度大于0.5 时，用户就会出现迷失特征，同时疲劳会快速增加。用户迷失度箱图如图6（b）所示。可以看到本文方法迷失度最小，用户评价最准确。

进化耗时Tt反映了算法的优化效率，同时也可以表征用户的疲劳性。交互时间越长，用户越容易疲劳。4 种方法的Tt箱图如图6（c）所示。可以看到本文方法耗时最短，说明本文方法用户操作时间最短，用户最不容易疲劳。

通过实验结果与分析，本文方法对混合指标分组优化能获得分布性和延展性更好的Pareto前沿，深度学习预测隐式指标更准确，子种群并行进化能有效协调不同类型的指标优化。与对比方法相比，本文方法能获得质量更高的Pareto最优解集，人机交互性更好。

4 结束语

高维混合多目标优化问题包含不同类型指标，且数量较多，求解难度较大。本文提出一种针对该问题的并行进化优化方法。该方法基于目标相关性对优化目标分组，将高维混合多目标优化问题分解为若干子问题。为了实现目标分组，采用深度卷积神经网络预测隐式性能指标，降低用户操作负担。对于每个子优化问题，采用对应子种群并行进化，提高问题求解速度。通过室内布局优化问题验证该方法的有效性，并与其他多种相关进化优化方法进行比较。实验结果表明，本文方法能有效提高算法搜索性能，获得高质量Pareto最优解集。高维混合多目标优化问题的交互式进化求解过程存在偏好波动，这会带来隐式指标的动态变化，进而改变Pareto最优解集。另一方面，如果显式指标存在时间变化参数，也会带来Pareto 最优解集的动态变化，这些都给问题求解增加了新的困难。因此，寻找Pareto最优前沿的特征点检测环境变化，并根据环境变化预测种群进化方向，是进一步研究的问题。