基于微分域电流过零点偏移特征的电抗器匝间保护新方法
陈继瑞,李宝伟,2,田宝江,朱云峰,王智勇,王瑞彬
(1.许继集团有限公司,河南 许昌 461000;2.华中科技大学 强电磁工程与新技术国家重点实验室,湖北 武汉 430074;3.国网河南省电力公司电力调度控制中心,河南 郑州 450052)
0 引言
超、特高压电网是我国现有电网构架的核心,装设高压并联电抗器(简称高抗)作为平衡系统无功、抑制系统过电压的成熟手段,已被广泛应用于电网输电线路中[1]。高抗是一种绕组铁芯带有气隙的大容量并联电感线圈,中性点位置一般装设有阻值可灵活选择的小电抗[2],故高抗的零序阻抗远大于变压器,零序电流较小。但当中性点不带小电抗时,高抗饱和后产生的零序电流将给匝间保护带来严峻考验。
高抗三相绕组出现不对称饱和后等效于在绕组内部串接1个零序电压源,电气特征主要表现为绕组电流幅值增加、计算电感值降低及出现零序电流,这些特征与匝间短路故障特征相似,容易引起匝间保护误动作。例如,某500 kV换流站高抗输电线路,在综合考虑潜供电流熄灭时间与经济性后,取消了中性点小抗。在线路合闸送电时,电抗器匝间保护出现了误动,现场波形特征为:绕组电流发生畸变、幅值增加;零序电流大于匝间保护定值;分相差差流为0。由上述特征可知,电抗器一次绕组出现饱和。
传统继电保护应对高抗饱和的方法,与变压器甄别励磁涌流类似,主要是识别相电流二次谐波含量大于定值后,进行按相或交叉闭锁保护。这虽能解决部分饱和问题,却面临着谐波制动定值整定困难及匝间故障动作灵敏度降低的问题[3-6]。文献[7]给出了一种利用电抗器相电流直流分量与二次谐波总含量,结合相阻抗测量值的变化特征,进行饱和与匝间故障识别的方法[7]。该方法能可靠识别典型的匝间故障与饱和工况,但对于匝间故障与饱和共存且非周期分量衰减较慢的情况,存在匝间保护动作灵敏度不足的问题。文献[8]在差动电流二次谐波含量小于经验值工况下,给出一种通过差流采样值特征识别变压器励磁涌流的方法,该方法并未考虑电流过零点前后采样峰值间距的对称度特征,在铁芯饱和不严重且二次谐波含量低于经验值时,存在空投饱和保护误开放的问题。但该文献给出了一种电流采样值特征量化识别故障与饱和的思路。
本文以不带中性点小抗的电抗器为研究对象,分析了不同电压合闸角及有无中性点小抗等工况下,电抗器空投饱和后的励磁电流特征,阐明了电抗器饱和机理,提出一种基于微分域电流过零点偏移特征的电抗器匝间保护新方法。该方法利用电抗器空投饱和后,微分域相电流过零点前后半波的采样峰值间距小于工频特征(未饱和)下相电流过零点前后半波的采样峰值间距的特征(即采样峰值间距值发生偏移),对匝间故障与饱和进行识别。当采样峰值间距偏移度小于阈值时,识别为饱和闭锁匝间保护,否则识别为故障,经短时间延时后开放匝间保护。对于匝间故障与空投饱和共存工况,利用电抗器磁通饱和前,励磁电流线性区内各时刻电感的均方根值特征来识别匝间故障与饱和。若线性区内各时刻电感均方根值大于阈值,则识别为空投饱和,闭锁匝间保护;否则识别为匝间故障,经短时间延时后开放匝间保护。本文方法不仅可以快速、准确地识别高抗饱和与匝间故障,还避免了谐波闭锁带来的定值整定困难及匝间故障动作灵敏度低的问题。最后通过仿真验证了本文方法的正确性和有效性。
1 高抗饱和机理及匝间保护误动原因分析
1.1 高抗绕组饱和机理分析
高抗绕组与变压器绕组结构不同,为了平衡漏磁及系统无功,高抗绕组铁芯内部带有气隙[9]。标准的高抗绕组伏安曲线特性要求1.5UN(UN为额定电压)以下伏安特征基本为线性,即1.4UN~1.7UN平均连线斜率不低于线性斜率的50 %[10]。因此,高抗与变压器空投饱和时的涌流特征不能一概而论。
1)高抗空投饱和机理分析。
以单相高抗绕组模型为例,绕组模型等效电路如图1所示。图中:M为绕组漏感;L为绕组自感;U为绕组端电压。忽略绕组内阻影响,绕组端电压方程如式(1)所示。
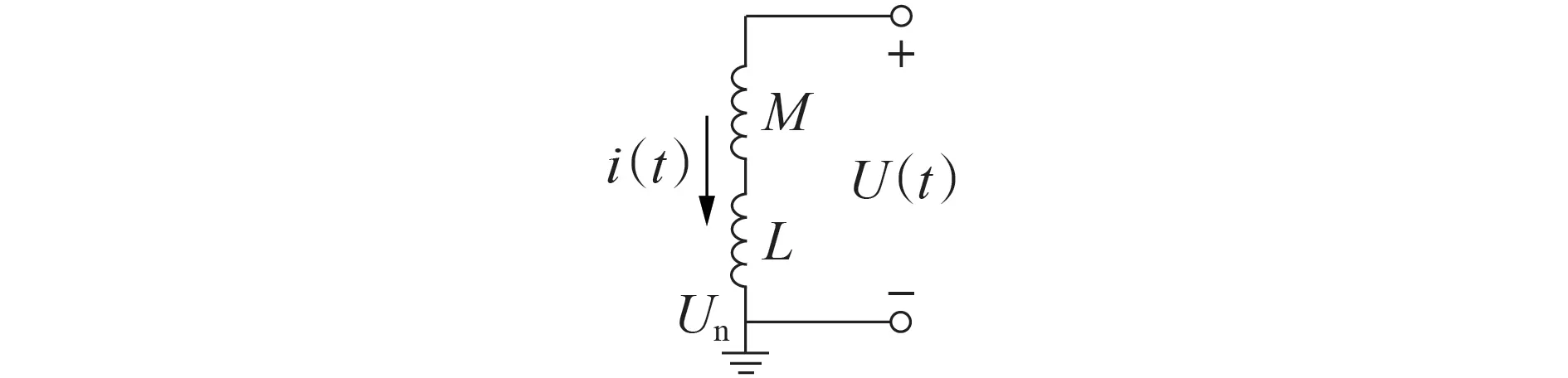
图1 主电抗器绕组等效模型图Fig.1 Equivalent model diagram of main reactor winding

式中:Un为中性点小抗绕组端电压,无中性点小抗时Un=0;Lz=L+M为绕组的总电感;ψM为漏感磁通;ψL为自感磁通;ψz=ψL+ψM,为绕组的总磁通。
假设高抗绕组总磁通为:

式中:ω为角频率;ψφ=(U-Un)/ω,为稳态磁通;ψr为剩磁;τ为时间常数。
由于高抗铁芯存在气隙,可忽略剩磁影响。当电压0°合闸时,半个周期(即α=π)时稳态绕组总磁通最大可达ψz≈2ψφ,此时绕组总磁通大于1.5ψφ进入磁通饱和区,绕组电流出现饱和特征。
2)中性点小抗对高抗涌流抑制机理分析。
当空投带中性点小抗的高抗时,由式(1)可知,当某相绕组铁芯饱和时,Un≠0,主电抗器绕组上磁通产生的感应电压将减小为U-Un,ψz也将减小,绕组饱和程度受到抑制,抑制程度与中性点小抗绕组端电压的大小及相位有关。
另外,目前实际运行系统中,中性点小抗值一般按主电抗值的1/3来选取[2]。因系统的零序阻抗远小于主电抗值,当空投带中性点小抗的高抗时,相当于系统零序阻抗与高抗电抗值相当,这大幅增加了系统阻抗值,涌流特征会被明显抑制。
1.2 高抗匝间保护误动原因分析
对于超、特高压交流输电线路的高抗而言,为了提高弱匝间故障下匝间保护的灵敏度,一般不配置二次谐波制动,同时匝间保护的零序电流启动定值也设置得较低,一般为10 %~20 % 的高抗额定电流。
现场误动的高抗匝间保护原理判据主要由零压零流比幅式的零序功率方向元件、零序阻抗测量元件及零序电流启动元件组成[11-15]。
1)零压零流比幅式的零序功率方向元件原理。电抗器发生区外单相接地故障时,零序电流相位滞后零序电压;电抗器发生区内单相接地或匝间故障时,零序电流相位超前零序电压。
2)零序阻抗测量元件原理。电抗器的一次零序阻抗一般为几千欧姆,而系统的一次零序阻抗通常为几十欧姆。电抗器发生区内故障时,端口测量零序阻抗为系统零序阻抗;电抗器发生区外故障时,端口测量零序阻抗为电抗器本体零序阻抗。利用电抗器本体阻抗与系统零序阻抗在数量级上的差异,可有效识别出电抗器区内和区外故障。
3)零序电流启动元件原理。高抗发生区内匝间或接地故障时,等效于电抗器内部存在1个零序电压源,在高抗与系统之间的回路中将产生零序电流,可利用零序电流来识别高抗匝间故障。
某500 kV换流站高抗匝间保护误动的事故波形中,高抗饱和后相电流IA、IB、IC及首端零序电流3I0有效值见图2,高抗饱和后零序电压采样值3U0、零序电流采样值3I0及零序测量阻抗Z0的时序图见图3。由图可知:空投高抗后B相电流明显出现涌流和衰减非周期分量;零序电流最大值为0.3 A左右;零序测量阻抗在0~60 Ω范围内波动;零序电流相位超前零序电压。现场匝间保护零序电流启动定值为0.126 A,零序阻抗定值为60 Ω,则可知满足匝间保护动作条件,现场高抗匝间保护动作。
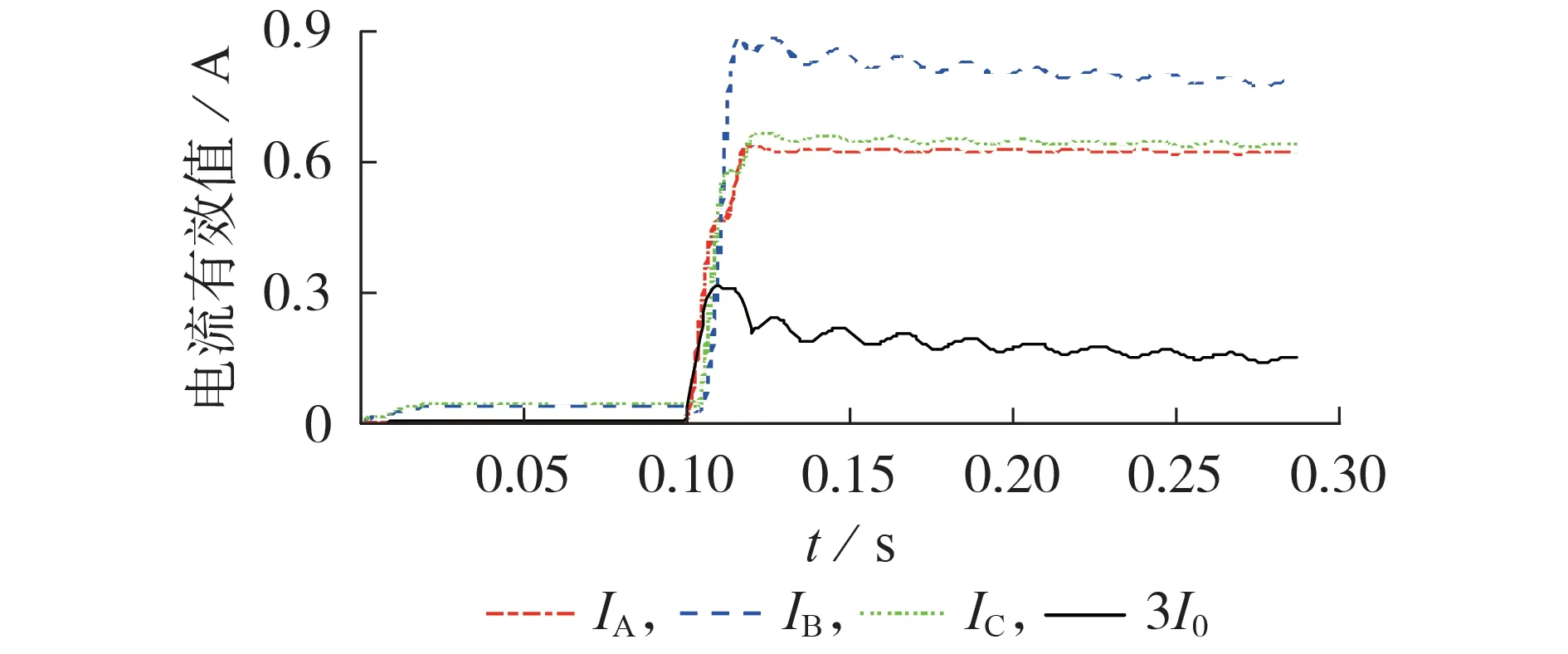
图2 高抗饱和电流特征图Fig.2 Characteristic diagram of current with high voltage shunt reactor saturation

图3 高抗饱和零序电气量特征图Fig.3 Characteristic diagram of zero-sequence quantities with high voltage shunt reactor saturation
综上所述,要提高匝间保护空投的可靠性,还是要回到饱和与匝间故障识别的问题上来。本文从高抗空投饱和、匝间故障及饱和与匝间故障共存等方面开展研究,探索高抗饱和与匝间故障的电气量特征变化规律,从而识别饱和与匝间故障。
2 高抗饱和与匝间故障识别方法
2.1 微分域电流过零点峰值间距偏移方法
由第1节可知高抗饱和需满足绕组总磁通大于1.5ψφ条件,在忽略剩磁的情况下,由式(2)可计算得到高抗进入磁通饱和区前1个周期内至少有1/4周期长度的线性区。在磁通进入饱和区后励磁电流会明显增加,在励磁电流最大时出现拐点,对应的微分域电流出现采样值过零点。以现场空投高抗饱和的误动波形为例,分析微分域电流过零点的电气量特征,微分域电流波形特征如图4所示。

图4 空投饱和微分域电流波形图Fig.4 Schematic diagram of current waveforms in differential domain during no-load closing saturation
由图4可知:在6 ms时刻空投高抗后出现原始相电流;15 ms时刻磁通进入饱和区,电流快速增加;17.5 ms时刻电流达到最大峰值,同时拐点出现,电流快速减小;20 ms时刻电流退出饱和;对应的微分相电流在15 ms时刻出现正峰值,17.5 ms时刻出现过零,20 ms时刻出现负峰值,过零点前后正负半波采样峰值的时间间距Δt≈5 ms,远小于工频正弦波峰峰值时间10 ms,这也是高抗存在较长线性区的典型特征。
高抗相电流微分变换的计算方法如式(3)所示。

式中:iφ为原始相电流采样值;iWφ为微分域相电流采样值;n表示第n个采样点;ΔT为单个采样间隔。
微分域相电流过零点时刻前后半波采样峰值间距偏移度计算方法如式(4)所示。
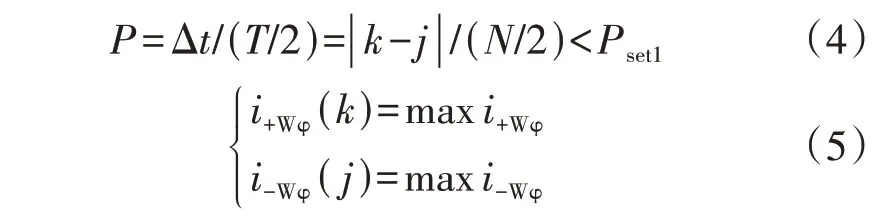
式中:P为该相微分域电流过零点时刻前后正负半波采样峰值间距偏移度;T=NΔT,为采样周期,N为单周期采样点数;k、j分别为正、负半波峰值对应的时刻;Δt=| |k-jΔT,如图4所示;i+Wφ(k)、i-Wφ(j)分别为计算得到的Δt对应的微分电流正、负半波峰值;maxi+Wφ、maxi-Wφ分别为正、负半波微分域电流采样值最大值;Pset1为偏移度门槛值。
若任一相微分电流满足式(4)则识别为高抗空投饱和,闭锁匝间保护;否则识别为匝间故障,经延时Tdelay后开放匝间保护。
2.2 磁通线性区电感均方根值特征方法
考虑到高抗空投饱和与匝间故障共存时,高抗饱和特征会使微分域相电流满足式(4),从而闭锁匝间保护,本文利用磁通线性区内的电感值特征来识别匝间故障,开放匝间保护。
令uφ为高抗任一相电压采样值,对应的微分域电流采样值可由式(3)得到。由电压和微分域电流采样值可计算出对应时刻的高抗电感值Lφ,电感值计算方法如式(6)所示。

高抗磁通线性区按最短时间,即1/4的周期考虑,电感均方根值的计算方法如式(7)所示。

式中:LEφ为电感均方根值;Lset1为均方根电感门槛值。
式(7)为按N/4数据窗滑动计算,只要高抗匝间故障存在,计算得到的电感均方根值就会小于Lset1,经延时Tdelay后快速开放匝间保护。
基于微分域电流过零点偏移特征的匝间保护新方法的动作逻辑如图5所示。

图5 电抗器匝间保护新方法动作逻辑图Fig.5 Logic diagram of novel method of reactor inter-turn protection
2.3 仿真验证
1)高抗绕组饱和机理验证。
某500 kV换流站高抗线路的主接线拓扑如附录A图A1所示。图中:S1和S2为无穷大系统,电压等级为550 kV;Line0为系统等效线路;Line1为带高抗的输电线路;现场高抗模型参数如附录A表A1所示。通过搭建RTDS仿真模型,使用现场的V-I曲线参数,对图A1中的主接线拓扑进行仿真试验,模拟合闸开关BRK2空投电抗器。分别在带中性电抗器(阻值为300 Ω)(工况a)和不带中性电抗器(阻值为0)(工况b)下,控制线路Line1A相电压在0°~90°范围内多次空投高抗,电抗器三相绕组电流、谐波含量及零序电流的数据如表1所示。表中:hA、hB、hC为三相二次谐波含量。电抗器一次额定电流Ie=0.189 kA。

表1 2种工况下高抗涌流特征对比Table 1 Comparison of inrush current characteristics of high voltage shunt reactor between two conditions
由表1可见:在A相电压0°合闸且不带中性点小抗时,A相电流约为0.26 kA(1.38Ie),零序电流约为0.06 kA(0.32Ie);在A相电压0°合闸且带中性点电抗器时,A相电流约为0.25 kA(1.32Ie),零序电流约为0.03 kA(0.16Ie);随着合闸角递增,2种工况下的A相电流量值和二次谐波含量也呈现递减趋势,带中性点小抗工况下,零序电流量值减小约一半,尤为明显。上述结果验证了高抗的相电流涌流特征受合闸角影响较大,零序电流特征受中性点小抗影响较大,这是导致现场电抗器匝间保护误动的主要原因。
2)本文所提匝间保护方法的动作性能验证。
在图A1不带中性点小抗的高抗模型基础上,模拟了多次A相电压0°~90°合闸角下高抗空投饱和、正常运行发生3 %~10 % 匝间故障及空投于3 %~10 %匝间故障工况时的高抗试验,以验证本文所提匝间保护方法的性能。
由表A1中的高抗参数可计算出高抗额定电感值Le=5.35 H。仿真时Pset1取值为0.75,Lset1取值为0.9Le=4.815 H,Tdelay取值为20 ms。
由于直接使用式(6)求解电感值时,在微分电流采样或电压采样过零点时会产生奇异解。因此,本文求解电感值时,先采用式(7)对电压和微分电流采样值进行处理后,再按式(6)计算电感值。
以A相电压0°空投高抗(工况1)为例,本文所提匝间保护新方法的仿真结果如图6所示,其他空投工况仿真结果类似,不再赘述。图中,开放状态1、0分别对应开放、闭锁保护,后同。由图6可知:A相电压0°空投时,高抗A相绕组饱和最严重,A相微分电流过零点峰值偏移度为0.5;另外,A相绕组线性区电感值在额定电感附近且均大于给定的阈值门槛4.815 H,因此,本文所提匝间保护方法的判据均不满足开放条件,匝间保护不动作。

图6 工况1下的仿真结果Fig.6 Simulative results under Condition 1
以高抗A相绕组正常运行时,发生3 % 匝间故障(工况2)为例,本文所提匝间保护方法的仿真结果如图7所示,其他匝间故障工况仿真结果类似,不再赘述。由图7可知:高抗A相绕组正常运行发生3 % 匝间故障时,高抗A相绕组微分电流幅值变大,三相微分电流过零点峰值偏移度为1;A相绕组电感值小于门槛4.815 H,B、C相绕组电感值大于门槛4.815 H。由此可见,本文方法的判据均满足开放条件,匝间保护动作。

图7 工况2下的仿真结果Fig.7 Simulative results under Condition 2
以高抗A相绕组空投于3 % 匝间故障(工况3)为例,本文所提匝间保护新方法的仿真结果见图8,其他空投于匝间故障工况仿真结果类似,不再赘述。由图可知,高抗A相绕组空投3 % 匝间故障时,高抗A相绕组微分电流幅值变大且A相微分电流过零点峰值偏移度为0.58,然而,A相绕组线性区电感值小于门槛4.815 H。因此,由此可见,本文方法的判据均满足式(7)所示的开放条件,匝间保护动作。
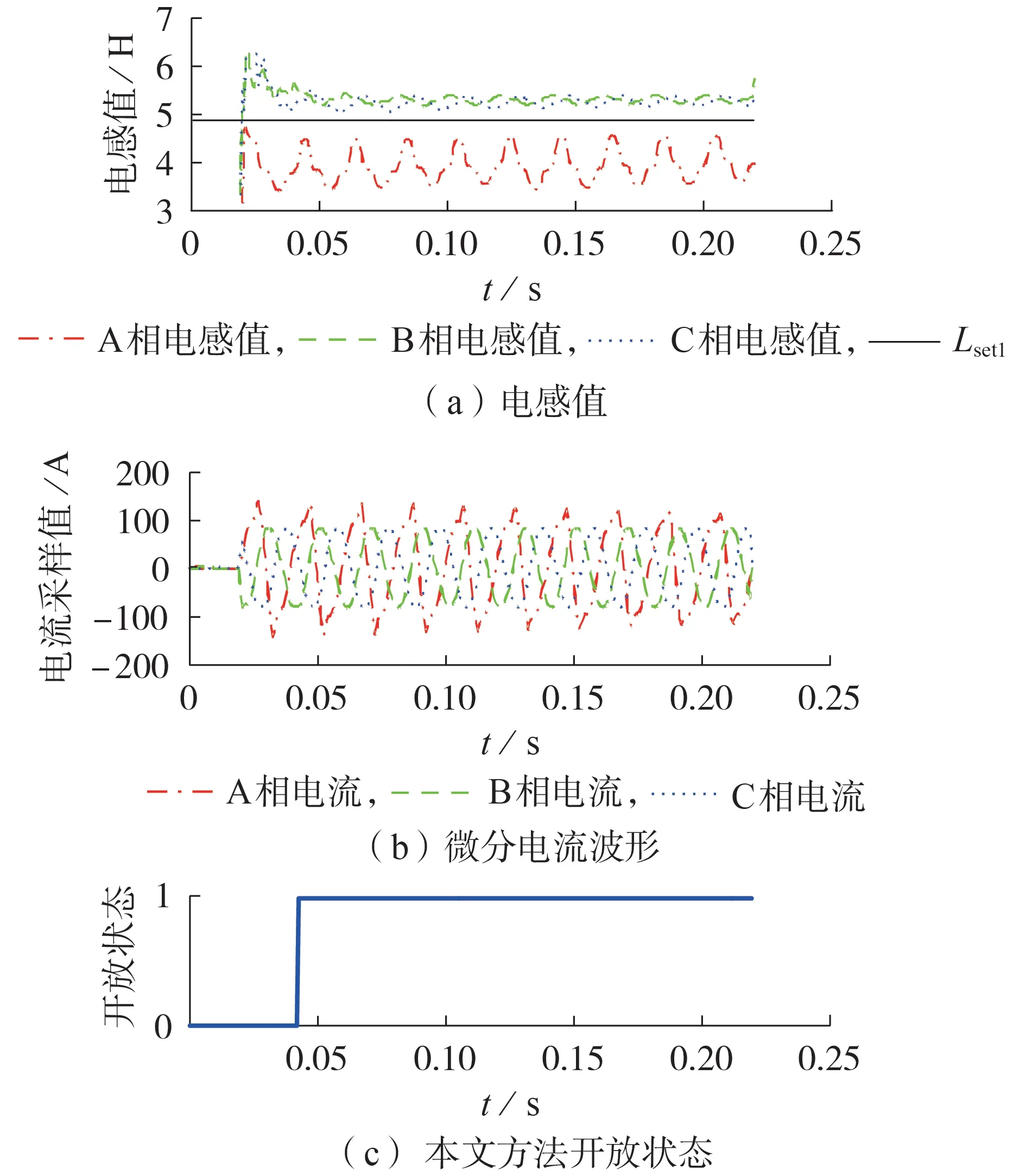
图8 工况3下的仿真结果Fig.8 Simulative results under Condition 3
综上分析可知,针对500 kV换流站不带中性点小抗的电抗器模型,空投高抗时匝间保护均可靠闭锁,正常运行3 % 以上匝间故障和空投3 % 以上匝间故障下,匝间保护均可靠动作,从而验证了本文所提匝间保护方法在识别匝间故障及空投饱和工况时的有效性与正确性。
3 结语
本文研究了500 kV换流站高抗空投饱和的机理,分析了中性点小抗对高抗空投饱和工况下,相电流和零序电流涌流特征更加严重是导致现场高抗匝间保护误动的主要原因;以高抗伏安曲线特征为基础,对高抗饱和区微分域电流过零点前后正负半波采样值特征进行研究,提出一种基于微分域电流过零点偏移特征的电抗器匝间保护方法。
本文所提方法通过识别微分域相电流过零点前后正负半波峰值间距与工频特征下相电流过零点前后正负半波峰值间距的偏移度,识别高抗空投饱和与匝间故障;对于高抗空投饱和与匝间故障共存工况,通过识别高抗空投饱和时线性区内均方根电感值接近额定电感,空投匝间故障时线性区内均方根电感值小于额定电感的特征,甄别出匝间故障。另外,本文所提方法避开了传统二次谐波制动识别饱和方法存在的定值整定困难及对匝间故障灵敏度不足的问题,同时该方法不改变原有匝间保护原理,对匝间故障动作灵敏度高。仿真结果验证了本文所提方法的正确性和有效性。
附录见本刊网络版(http://www.epae.cn)。

