基于区间优化算法的电力系统可靠性评估逆问题模型

彭吕斌，胡 博，谢开贵，孙 悦，黄 威，曹 侃，周鲲鹏

（1.重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400044；2.国网湖北省电力有限公司 电力科学研究院，湖北 武汉 430077）

0 引言

电力系统可靠性评估［1］从元件可靠性参数（component reliability parameter，CRP）、电气参数、系统结构参数等出发，通过可靠性建模、系统状态分析等过程，计算系统和节点可靠性指标。历经多年的研究和工程实践，电力系统可靠性评估已经发展成为相对完善的理论。然而，可靠性评估技术目前存在两方面的挑战。

挑战1：部分不准确的CRP影响了可靠性评估的应用价值。CRP是可靠性评估的基础和关键。一旦参数有误或缺失，就会导致错误的评估结果［2-3］，进而可能误导电力系统的规划、改造等决策，甚至影响未来规划系统的安全、可靠运行［4］。CRP通常由元件历史停运数据的统计分析而得。然而，可靠性数据统计工作具有复杂性、动态性，且易受人为因素影响，具体表现在以下几个方面：①历史停运记录难免存在错误或者无效的数据［2，5］；②元件可靠性随年份呈现动态变化，若历史数据未及时更新，则得到的参数值会不准确［2，5］；③停运数据的自动录入在我国尚未完全实现，而人工记录会受到公司和人员考核或者人为错误等主观因素的影响［5］。鉴于上述因素，CRP的准确性难以保证。因此，在加强设备停运数据管理的同时，有必要寻求对电力CRP进行校核和补正的途径。当今，由于负荷用户对停电事件的关注与日俱增，且随着先进量测设备［6］在电网中的安装普及，电网运营者通常有详实准确的停电事件记录，而停电记录易转换为可靠性指标。因此，系统／节点可靠性指标易于获得并且准确度较高［2，5］。通常在给定系统电气参数、网络结构、运行参数等后，可以认为电力CRP和系统／节点可靠性指标间具有一一对应的关系［2-3］，如果能够从已知的可靠性指标入手求取或校正CRP，则不失为一种合理的方法。

挑战2：在电力系统优化、设计和改造问题中，为达到预期的系统可靠性水平，有时需要确定元件的可靠性参数。这同样涉及了由可靠性指标出发计算CRP的过程。现有研究一般是通过建立优化模型来求解可靠性参数，在求解过程中通过可靠性评估“正向”过程计算系统可靠性指标。然而，由于可靠性评估的计算复杂度大，且缺乏解析表达形式，关于优化模型的有效求解十分困难，解的质量和计算效率都较低，难以实现较为准确的投资。

以上两方面挑战从本质上均可归纳为如何由可靠性指标“逆向”计算CRP，若能直接从“逆向”过程的角度入手，对“逆向”计算模型、方法进行系统性的研究，跳出可靠性评估“正向”过程思路的限制，则有潜力较好地解决以上2个问题。据此，文献［7］首次提出电力系统“可靠性评估逆问题（inverse problem of reliability evaluation，IPRE）”的概念。IPRE理论的提出，为实际工程中众多由已知可靠性指标计算CRP的问题提供了全新的解决思路。逆问题理论能为电力系统的规划设计、改造、检修等工程领域的决策提供量化参考，如计算缺失的CRP、校正错误可靠性参数、在系统设计或改造中优化确定元件应达到的可靠性水平等。根据需解决的工程问题，逆问题可分为面向部分未知可靠性参数求取的逆问题、面向错误可靠性参数校正的逆问题、面向可靠性参数优化的逆问题等。

当前针对电力系统IPRE的研究还很鲜见。文献［7］建立了发输电系统IPRE的方程组模型，并将其应用到系统可靠性改造场景中。文献［8-9］主要研究了方程组模型的求解算法。文献［10］建立了配电系统的IPRE模型，用以求取一部分元件的可靠性参数。但以上研究均只针对IPRE中待求可靠性参数个数与已知可靠性指标个数相等的这一特殊情形，所建立的模型和所提出的求解方法较难推广至一般情形。另外，发输电系统可靠性指标是有关可靠性参数的多维、高度非线性函数，这使得发输电系统IPRE的求解较为困难。对于可靠性参数校正［11-12］、可靠性参数优化设计［13-14］等需要刻画可靠性指标与参数关系的问题，现有研究采用梯度（或Newton）下降法［11-13］或者群体智能算法［14］求解。然而，常规梯度（或Newton）下降法依赖于良好的初值解，可能会收敛到局部最优，而局部最优解并非参数的准确值；群体智能算法不仅同样存在早熟问题，而且难以处理复杂的约束。因此，选择性能良好的全局优化算法是IPRE研究中的重点。

针对已有逆问题研究的不足，本文基于可靠性指标解析计算函数，为综合计及已知可靠性指标个数大于、等于或小于待求参数个数的3种情形，提出逆问题的一般性模型，并提出基于改进区间优化算法（interval optimization algorithm，IOA）的逆问题求解方法。通过算例分析验证了本文所提模型和方法能够求得准确的可靠性参数，并在一定程度上提升了计算效率。

1 IPRE

IPRE指由已知的系统或节点可靠性指标求取未知的CRP。根据该定义，CRP补全与校正、参数优化设计等均属于IPRE的范畴。图1说明了IPRE的概念，图中可靠性指标包括失负荷概率（loss of load probability，LOLP）、失负荷频率（loss of load frequency，LOLF）和期望缺供电量（expected energy not supplied，EENS）。IPRE涉及的相关概念和因素如表1所示。

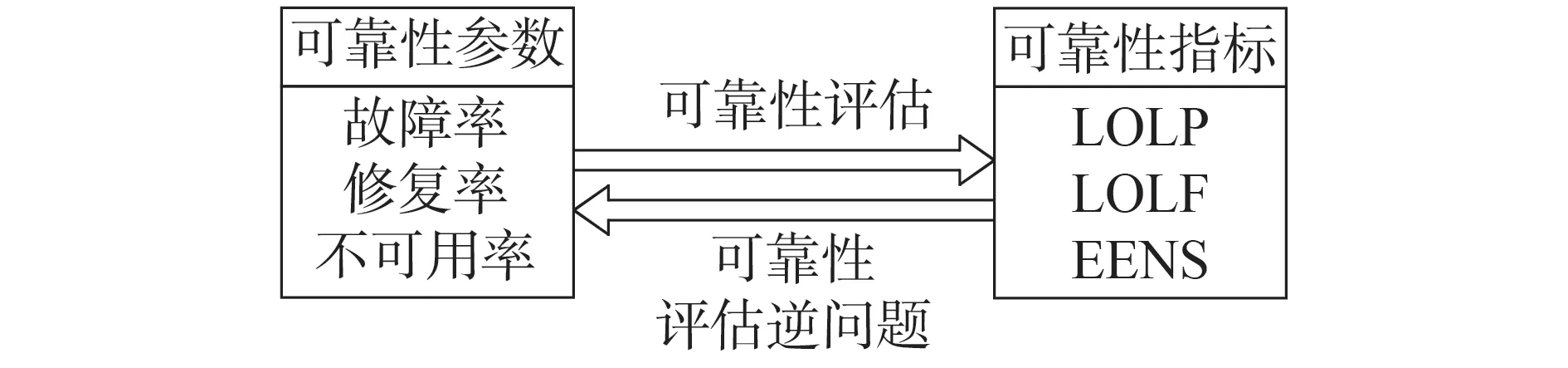
图1 IPRE的概念Fig.1 Concept of IPRE

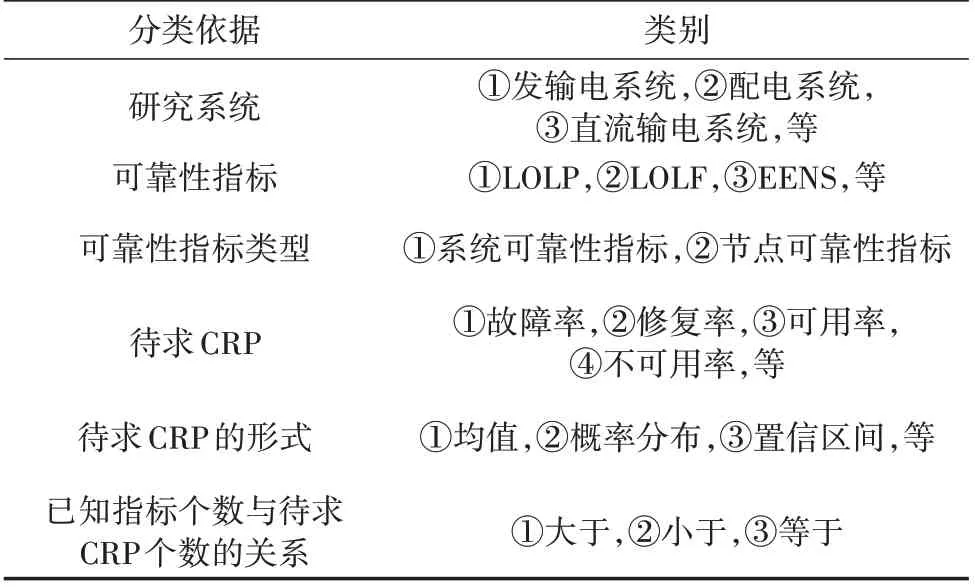
表1 IPRE的相关概念和因素Table 1 Related concepts and elements for IPRE

本文主要关注发输电系统的IPRE，待求CRP的形式采用常用的均值。在研究IRPE时，本文假设给定的可靠性指标准确，除待求CRP外，其他的CRP均已知。利用已知的可靠性指标值和可靠性指标关于待求CRP的函数关系，可以构造表达IPRE的非线性方程组，其一般形式如下：

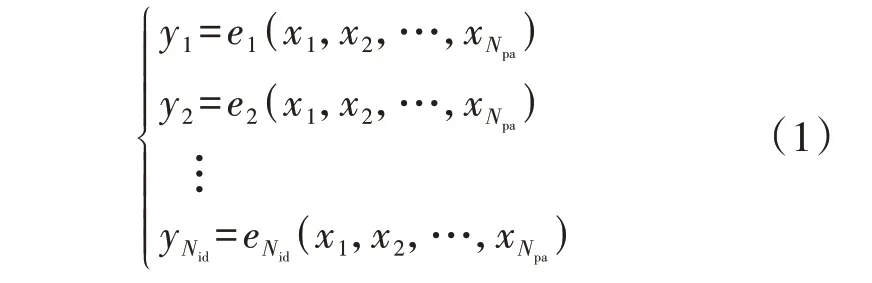
式中：Npa为待求CRP的个数；Nid为已知可靠性指标的个数；y1、y2、…、yNid为给定的系统或节点可靠性指标；x1、x2、…、xNpa为待求的CRP；e1、e2、…、eNid为各可靠性指标关于CRP的函数关系，具体表达式将在第2节中介绍。

根据非线性方程组式（1）中待求量个数Npa与方程个数Nid的大小关系，IPRE可以分为如下3种情形：

1）若Npa=Nid，则式（1）是Nid维的非线性方程组；

2）若Npa＜Nid，则可将式（1）转化为非线性优化问题求取未知可靠性参数；

3）若Npa＞Nid，则式（1）可能会有无限个解。

现有IPRE研究均主要针对情形1），其求解方法不适用于另外2种情形。当Npa与Nid不相等时，可将非线性方程组转化为优化问题求解。当Npa≤Nid时，大多数情况下IPRE有唯一解。但当Npa＞Nid时，IPRE可能会出现无限个解。此时，若要从中确定唯一解，则需要结合具体工程场景的附加信息，构建对应于场景的逆问题模型。需要说明的是，对非线性方程组解个数进行判断较为困难，以上只是面向工程实际的一般规律。

2 可靠性指标的解析函数

为便于IPRE问题的求解，方程组式（1）的每一个等式中可靠性指标宜表达为待求可靠性参数的解析函数。下面给出基于状态枚举法的可靠性指标关于待求CRP的解析函数。以LOLP指标的解析函数为例，介绍可靠性指标解析函数的推导。LOLP指标值δLOLP的计算公式为：

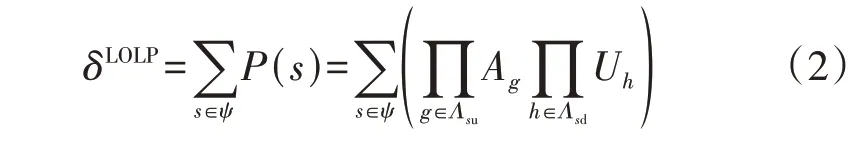
式中：ψ为枚举产生的失负荷系统状态集合；P(s)为系统状态s发生的概率；Λsu和Λsd分别为系统状态s下处于正常和故障的元件集合；Ag和Uh分别为元件g的可用率和元件h的不可用率。假设电力系统有n个元件，每个元件考虑正常和故障2个状态，且元件故障的发生相互独立。将待求CRP涉及的元件个数记为m，这m个元件称为所研究元件，剩余n-m个元件称为其他元件。所研究元件一共有M=2m个组合状态，其中第j个组合状态记为Fj。例如，假设有4个待求CRP，分别为元件1的故障率λ1、元件2的故障率λ2和修复率μ2、元件3的修复率μ3，则m=3、M=8，其组合状态见表2。表中：“1”和“0”分别表示对应元件处于故障和正常状态；F1表示元件1故障而元件2和元件3正常的一种组合状态，其他类似。

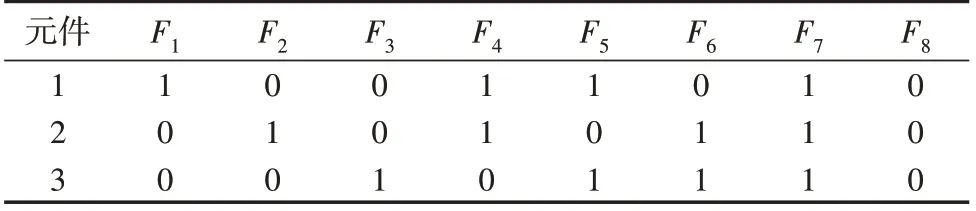
表2 3个所研究元件的组合状态Table 2 Composite states of three studied components

根据上述3个所研究元件所处的组合状态，可以将系统状态集合ψ拆分为8个子集合，分别记为φ1、φ2、…、φ8。相应地，式（2）可拆分为8项之和，具体如式（3）所示。

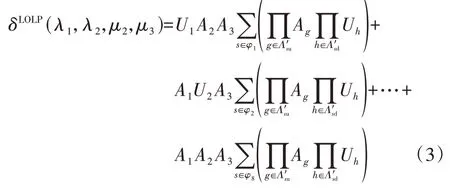
式中：Λ′su和Λ′sd分别为系统状态s下处在正常和故障状态的其他元件的集合。式（3）表示LOLP是4个待求CRP的函数。3个所研究元件的可用率和不可用率如式（4）所示。

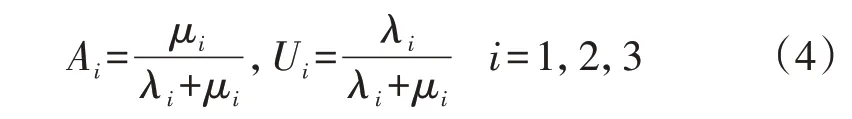
进一步地，LOLP指标的解析函数可写为：

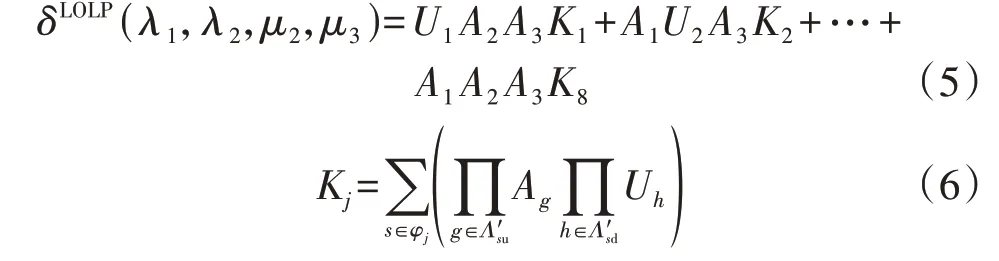
式中：φj（j=1，2，…，8）为所研究元件处在第j个组合状态对应的系统事件集合；Kj为当给定的所研究元件处在组合状态Fj时系统的LOLP。当系统的电气参数、网架结构和运行参数确定时，Kj只取决于nm个其他元件的可靠性水平。由于假设其他元件的可靠性参数已知且不变，因此，Kj是一个常数，其可通过一次可靠性评估求得［7］。将上述m=3的例子扩展为一般形式为：

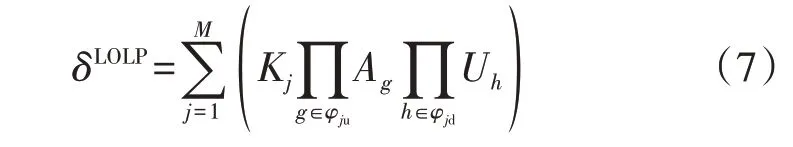
式中：φju和φjd分别为组合状态Fj下处于正常和故障状态的元件集合。

采用类似的推导过程，LOLF和EENS的解析函数分别为：

式中：δLOLF和δEENS分别为LOLF和EENS的指标值；λg和μh分别为元件g的故障率和元件h的修复率；H(s)为系统状态s下的削负荷量；T为单位时间长度，本文取1 a（8 760 h）；与Kj类似，Jj和Lj（j=1，2，…，M）为一组常数，它们可通过一次可靠性评估计算得到［7］。需要说明的是，在确定系数Kj、Jj和Lj时需要判断给定的系统状态是否失负荷及计算其削负荷量H(s)。本文算例中采用的是基于直流潮流的削负荷策略，实际系统的削负荷策略可能会更为复杂。然而，负荷削减方式不影响逆问题的解析建模及应用。当针对某实际系统建立其可靠性指标解析函数时，只需在可靠性评估中采用该系统实际的削负荷策略计算H(s)即可。

式（7）—（9）即为可靠性指标关于待求CRP的解析函数。当可靠性指标和系数Kj、Jj、Lj是已知量，待求量是所研究元件的未知CRP时，基于式（7）—（9）可构建方程组式（1）。上述基于状态枚举法的解析函数的推导和建立过程见文献［7］。此外，基于蒙特卡罗模拟法也可以推导类似的解析函数［15］，本文不再赘述。

3 IPRE的优化模型

不论式（1）中的Npa和Nid是何种大小关系，基于最小二乘估计（least squares estimation，LSE）原理，方程组式（1）都可以转化为非线性优化模型（记为模型P1）统一求解，具体如下：

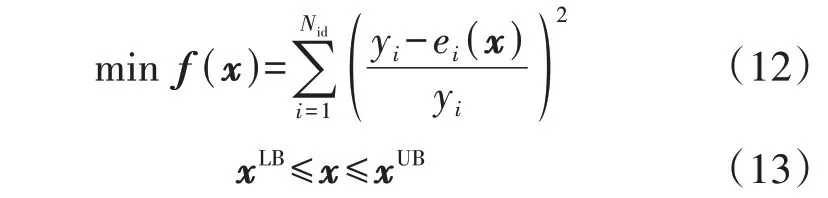
式中：x为待求CRP构成的向量，包括元件故障率、修复率等，是模型P1的决策变量；yi为元件i模型的输入数据，包括已知的系统或节点LOLP、LOLF和EENS指标值；xUB、xLB分别为由工程经验得到的CRP的取值上、下限。模型基于可靠性指标解析函数，以可靠性指标的计算值与指标的已知值的偏差平方和最小为目标函数。式（13）表示决策向量x的上下限约束。

当Npa＞Nid时，模型P1可能会有无数解。此时，求解结果缺乏实际意义，无法直接应用在工程实践中。若想从中确定唯一解，则需要结合具体工程场景，在模型P1的基础上补充附加信息或设置边界条件，构建对应场景的逆问题模型（记为模型P2）。本节以规划场景中的可靠性参数求取为例，说明模型P2的构建。为满足预定的系统或节点可靠性指标要求，模型P2以元件投资（或改造）的总费用最小为目标函数来优化设计元件的可靠性参数，其计算公式如式（14）所示。

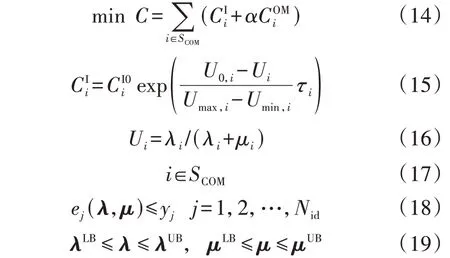
式中：SCOM为含待求可靠性参数的元件集合；为元件i的投资费用；C为元件i的年运维费用，可按投资费用的一定比例考虑；α为年金现值系数，与贴现率和设备经济寿命有关［16］，该系数将年费用折算到现值；U0，i和分别为元件i的基准不可用率和基准投资费用（其具体含义见第6节）；Umax，i、Umin，i分别为元件i不可用率的上、下限；τi为关于元件i的一个常数［17］；λ、μ分别为待求的故障率、修复率参数向量；ej(λ，μ)为对应于λ、μ的第j个可靠性指标的计算值；λLB、λUB分别为待求的故障率参数向量上、下限；μLB、μUB分别为待求的修复率参数向量上、下限；yj为对第j个指标的要求。式（14）表示总费用由元件投资费用和运维费用组成；式（15）表示投资费用是元件不可用率Ui的函数；式（18）表示需要满足的可靠性指标约束；式（19）表示待求元件参数的范围。在模型P2中，决策变量是待优化的CRP，例如Ui、λi和μi。可靠性指标值以预设的可靠性指标约束的形式呈现，在确定元件的可靠性参数时，考虑了CRP与投资费用间的关系。

需要说明的是，模型P1是通用的基础逆问题模型，其不依赖于具体工程问题，既可用于求取现有的CRP，也可用于在规划场景中求取未来应达到的可靠性参数。模型P2可视为模型P1存在无限解时的情形，是结合了附加信息的逆问题模型，模型P2依赖于具体工程问题。本节给出的模型P2仅是以面向规划场景的可靠性参数优化为例来说明模型的构建。针对其他工程问题，也可结合其中用于确定CRP的附加信息，构建出对应的模型P2。

4 IOA

逆问题模型具有强非线性。由于工程实践中通常只能获取待求CRP的粗略取值范围，而常规非线性优化算法依赖于初值解，因此难以求得准确的参数值。如引言所述，选择具有全局收敛能力的优化算法是逆问题研究的重点。

IOA用区间迭代替代常规算法的点迭代，通过区间分割和检验，可以保证找到最优解或判断当前区间内无解，该算法为IPRE的求解提供了新思路。然而，现有文献常用的IOA［7，18］只能适用于方程个数与待求变量个数相等的非线性方程组。为处理方程个数和变量个数不等的情况，本文采用改进的IOA来求解逆问题的优化模型。区间数和区间运算的概念见文献［19］。

4.1 基本IOA

4.1.1 模型P1的IOA

为便于介绍IOA，首先将模型P1写成如下紧凑形式：

式中：X为x取值的区间向量。

IOA的构造和改进的一个关键是区间删减工具的使用［20］。删减工具能够准确删除不可能存在最优值的区间。删减工具包括中点检测［21］、单调性检测［21］、凸性检测［20］、区间Newton法［20］等。其中，区间Newton法不仅可以删减区间，还具有检验解的存在性并迭代到精确解的能力，下面重点介绍区间Newton法。

若考虑模型P1待求变量的取值区间足够大，则最优点从驻点中产生。记目标函数f的梯度为g，J为向量g的雅可比矩阵，J(X)为J在区间向量X上的区间扩展，区间矩阵J(X)的中心为JC，JC的一个近似逆矩阵为Y。

寻找目标函数的驻点可转化为求方程组g=0的解。使用区间Newton迭代可找到方程组在指定区间X上的所有解。基本区间Newton算子的计算复杂度很大，已有一些研究对基本区间Newton算子进行了改进，常用的有区间Krawczyk算子，其迭代公式如下：

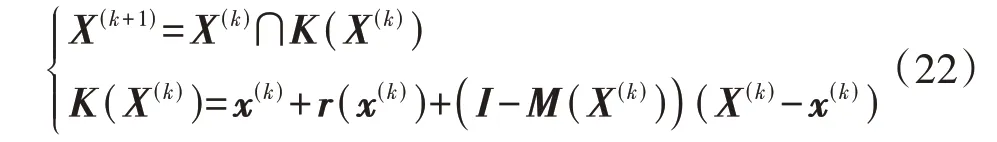
式中：k=0，1，…，为迭代次数；∩表示对符号两边的区间向量取交集；x(k)通常取X(k)的中点；I为单位阵；M(X(k))和r(x(k))计算公式如式（23）所示。

区间Krawczyk算子有以下3条性质［20］：①若x*使得g(x*)=0，且x*∈X(k)，则x*∈K(X(k))；②若X(k)∩K(X(k))=∅，则g=0在X(k)中无解；③若K(X(k))≠∅且K(X(k))⊂X(k)，则g=0在X(k)中必有解。利用区间Krawczyk算子的性质可判断在给定区间上是否有解。此外，若K(X(k))≠∅，K(X(k))⊂X(k)且W（K(X(k))）＜W（X(k)），则区间X(k)内有唯一解，其中W（·）表示求区间向量（·）的宽度。此时，以任意一点x(0)∈X(k)为初值，采用以下点Newton迭代公式，可得到解如式（24）所示。

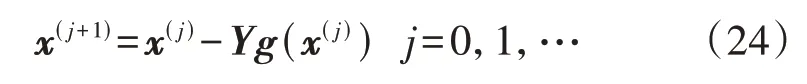
4.1.2 模型P2的区间优化求解算法

将优化模型P2写成如下的紧凑形式：

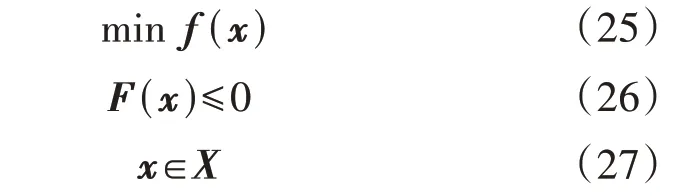
式中：F(x)≤0为式（15）—（19）的矩阵形式。

求解式（25）就是寻找约束域内的极小点。约束优化问题的极小点需要满足Fritz-John最优性条件（以下简称John条件）。记增广变量t为：

式中：u=[u0，…，ui，…，uNid]，为Lagrange乘子，并 且0≤ui≤1。将John条 件 写 成 关 于t的 函 数 组，并 记为φ(t)：

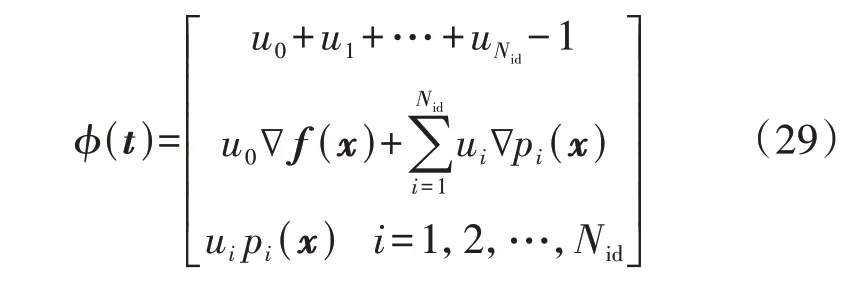
此时，在给定区间上，含约束的优化问题P2转化为求解如下的方程组：

至此，应用4.1.1节中的区间Newton法求解式（30），即可求解模型P2。需要注意的是，对求解过程中产生的每个区间，需要检验该区间是否满足约束。

4.2 IOA的改进措施

4.1节介绍了IOA的基本思路，但在实际使用中会面临计算量大的问题。利用区间删减工具可提高计算效率。针对具体的优化问题，不同的区间删减工具对于提升求解效率的效果不同。因此，结合逆问题数学模型的特点，在基本IOA的基础上，本文引入合适的区间删减工具，设计了改进IOA。下面将介绍选用的区间删减工具。

4.2.1 高斯塞德尔（Gauss-Seidel）技巧

本节利用Gauss-Seidel技巧改进区间Krawczyk算子，即为区间Krawczyk-Hansen算子［19］。该算子可以得到更狭窄的区间，迭代过程由以下的公式描述：

式中：Xi为区间向量X的第i个分量；H为区间Hi第k次迭代的数值；Mi，j为Krawczyk-Hansen系数矩阵M的第i行第j列元素；x为可行解xi第k次迭代的数值；r为中间变量ri第k次迭代的数值。区间Hi会比Krawczyk算子Ki更狭窄，因此可提高收敛速度。

4.2.2 包络一致性

在给定的区间上，合理应用包络一致性（hull consistency，HC）可减小区间宽度，或者排除不存在解的区间［20］。若有方程f(x)=0，又f(x)可以拆成d(x)和h(x)两项之差，即：

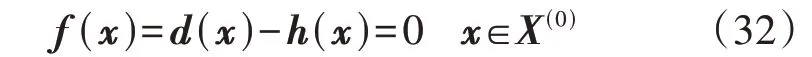
应用HC，可将区间X更新为：

若更新后的X为空集，则表明初始区间X(0)上不存在f(x)的零点。类似地，HC也可应用到不等式约束上。HC适用于求解IPRE，其详细分析见附录A。

5 基于IOA的逆问题求解流程

图2给出了基于IOA的电力系统IPRE的求解流程图。在求解逆问题时，根据待求CRP个数Npa和已知可靠性指标的个数Nid的大小关系，应当建立相应的模型和选择IOA。此外，根据解的情形，在逆问题求解过程中，可能会进行不同模型和算法之间的转换。关于图2的详细说明和IOA的流程分别见附录B和附录C。

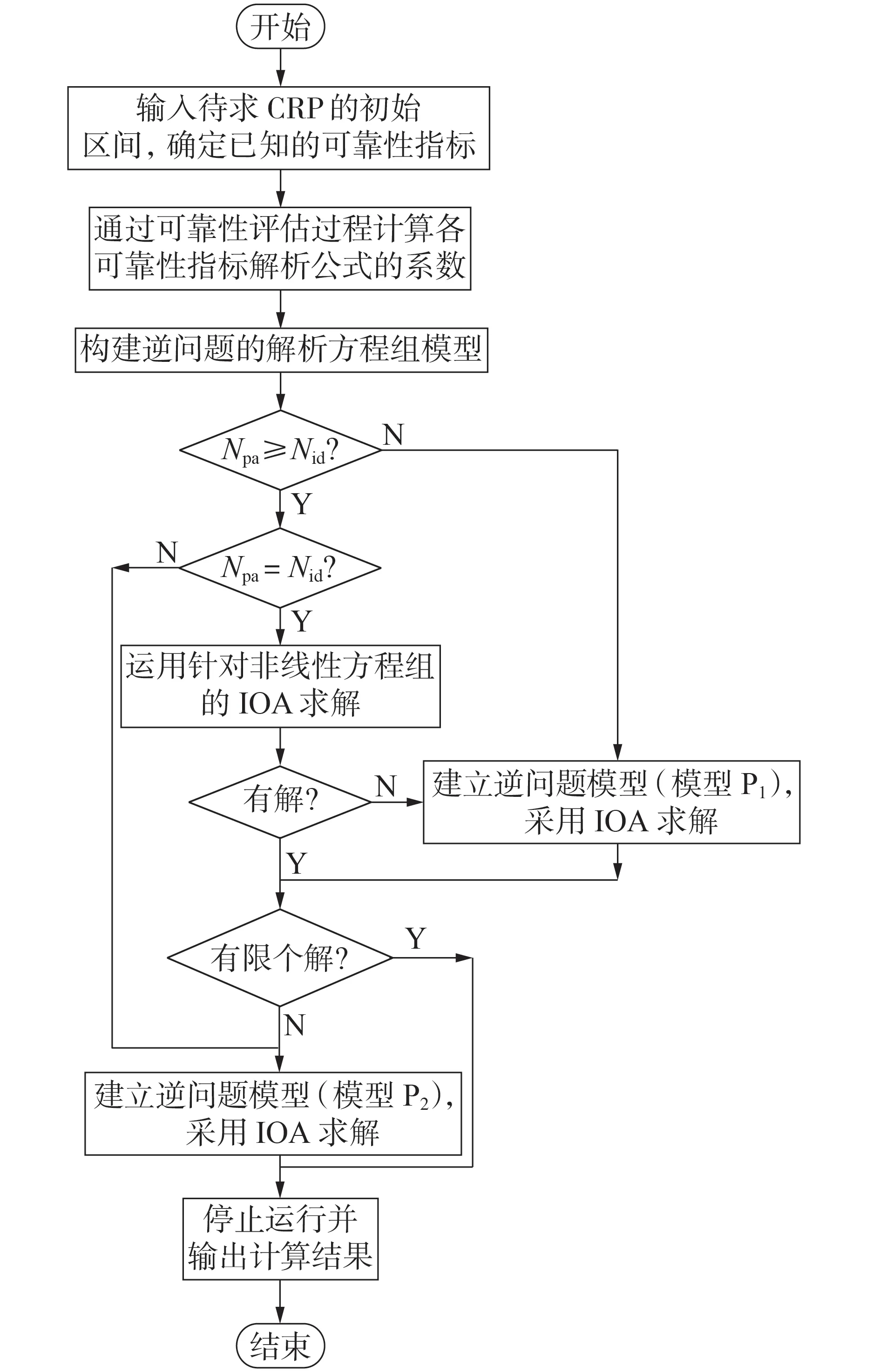
图2 IPRE的求解流程图Fig.2 Flowchart of solving IPRE

6 算例分析

本文基于RBTS［22］、IEEE-RTS的发输电系统［23］和1个91节点的实际电力系统（简称为CS系统）测试所提模型和求解算法的效果和性能。部分测试系统的参数见附录D。算例包括如下3个部分：逆问题模型P1的求解；逆问题模型P2的求解；比较所提改进IOA与区间Krawczyk算法［7］的计算效率。

首先，采用状态枚举法计算得到测试系统的可靠性指标，并将其视为逆问题的已知可靠性指标。测试系统的系统可靠性指标如表3所示。

表3 各测试系统的已知可靠性指标Table 3 Known reliability indices of test systems

6.1 逆问题模型P1的求解

6.1.1 IEEE-RTS系统的测试

为测试所提模型和算法的有效性，算例中将假设部分CRP待求。待求CRP有λG1-20MW、μG22、μG15-12MW、λL7、μL11、λL23这6个，其中λG1-20MW为节点1所连的全部20 MW容量机组的故障率，μG22为节点22所连机组的修复率，μG15-12MW为节点15所连12 MW机组的修复率，μL7为支路7的修复率，其他类似。在该逆问题中，假设位于同一节点的同类型同容量机组的CRP相同。若无特别说明，则下文中CRP符号的含义与之类似。机组和支路的编号与测试系统文献［23］给出的编号顺序一致。利用的可靠性指标有6个，包括节点15、节点18和系统的LOLF、EENS指标。结合工程经验，待求CRP的初始取值区间设置为其真值的50 % 至其真值的2倍。除了用IOA求解逆问题模型P1外，本节还用其他常见的非线性优化算法来求取未知CRP，包括内点法（interior point algorithm，IPA）［24］和信赖域反射法（trust region reflective algorithm，TRR）［25］。采用不同算法的求取结果如表4所示，此外，表4还展示了非线性优化算法的初值解，表中故障率和修复率单位均为次／a，后同。

表4 P1下不同算法的可靠性参数求取结果（IEEE-RTS系统）Table 4 Results of reliability parameters with different algorithms under P1（IEEE-RTS system）

由表4可见，IOA的精度高于2种常规非线性算法。常规非线性算法得到的机组CRP结果的精度较好，但是输电线路CRP的误差较大。这主要是因为可靠性指标对于输电线路CRP不敏感，导致常规非线性算法容易收敛到局部最优，较难达到全局最优。

6.1.2 CS系统的测试

本节采用CS系统以测试模型和IOA在大规模实际系统上的性能。该系统由中国某跨省的实际系统简化而来，包含64台机组和173条输电线路，总装机容量为10 684 MW，峰荷为9 732 MW。设已知可靠性指标的个数为11，待求CRP个数为10。待求CRP的初始取值区间为其真值的50 % 至其真值的2倍。IOA和IPA以及TRR算法的求解结果如表5所示。

表5 P1下不同算法的可靠性参数求取结果（CS系统）Table 5 Results of reliability parameters with different algorithms under P1（CS system）

由表5也可得到与表4相似的结论。针对CS系统的案例，常规非线性算法的修复率结果误差很大。

6.2 逆问题模型P2的求解

对于任一元件i，定义它的基准不可用率U0，i及对应的基准投资费用CI0i关系如下：当优化后的不可用率低于基准不可用率时，投资费用会比基准投资费用高，反之则低。元件的基准不可用率设定为测试系统文献［22-23］给出的原始不可用率，并假设机组元件的基准投资费用与它的容量成正比，设发电机的CI0为104$／MW，输电线路的CI0为104$／km，变压器的CI0为 $ 105。所有元件的投资费用计算公式（式（15））中的系数τ统一取7.0。对于逆问题模型P2，本节还使用一种元启发式优化算法——粒子群优化（particle swarm optimization，PSO）算法，以对比验证IOA的性能。

6.2.1 RBTS系统的测试

假设有6个待求CRP，如表6所示。各CRP的取值区间均设置为其基准值的50 % 至其真值的2倍，6.2.2节和6.2.3节设置与此相同。利用的可靠性指标有系统LOLF和EENS指标2个。PSO算法的种群规模设置为15，最大迭代次数为150次，并重复运行5次。表6给出了算法的结果对比，其中PSO算法为5次运行的最优结果，IOA对应的总费用为计算的总费用区间的中点。

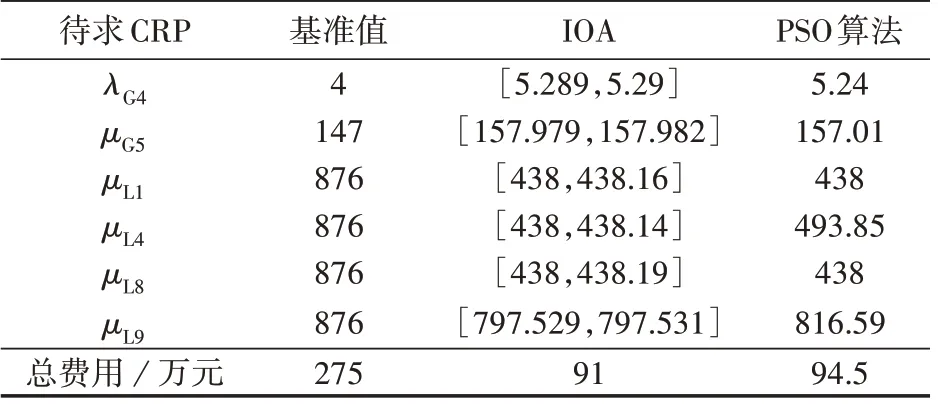
表6 不同算法的可靠性参数求取结果（RBTS系统）Table 6 Results of reliability parameters with different algorithms（RBTS system）

6.2.2 IEEE-RTS系统的测试

待求的CRP有9个，利用的可靠性指标有系统LOLP、LOLF和EENS指标3个。算法的求解结果如表7所示。

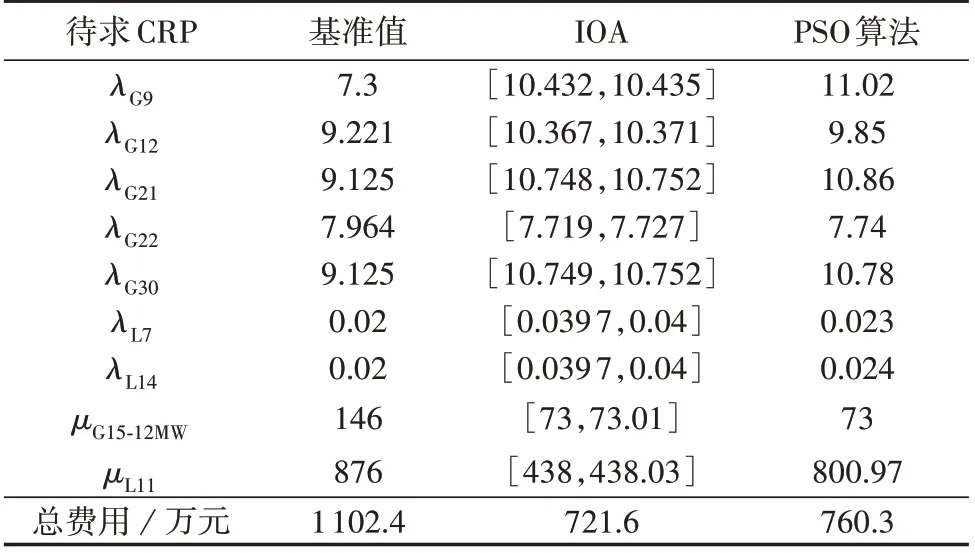
表7 P2下不同算法的可靠性参数求取结果（IEEE-RTS系统）Table 7 Results of reliability parameters with different algorithms under P2（IEEE-RTS system）

比较表6或表7中的总费用基准值和算法的优化结果可知，在给定的可靠性参数优化模型以及经济性参数下，存在比基准可靠性参数取值及对应的基准费用更优的可靠性参数取值组合，且IOA得到的投资费用结果要明显好于PSO算法。这表明在处理含可靠性约束的逆问题P2时，IOA具有较好的精度，而元启发式算法（PSO算法）的精度不够高。另外，表7中2种算法的计算结果的差距比表6要大，这可能是因为PSO算法的寻优性能随着变量维度的增加而劣化。图3展示了表7中采用2种算法分别求取最优总费用时的迭代曲线，图中PSO1—PSO4对应4次独立重复的PSO算法迭代过程。

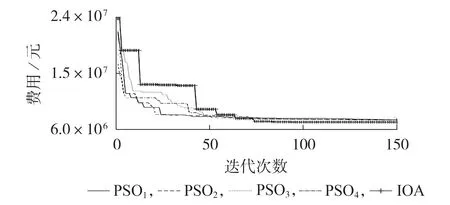
图3 IOA和PSO算法在求取总费用时的迭代曲线Fig.3 Iteration curves of IOA and PSO algorithm for obtaining total cost

6.2.3 91节点CS系统的测试

待求的CRP有10个，利用的可靠性指标有系统LOLP、LOLF和EENS指标3个。算法的求解结果如表8所示。

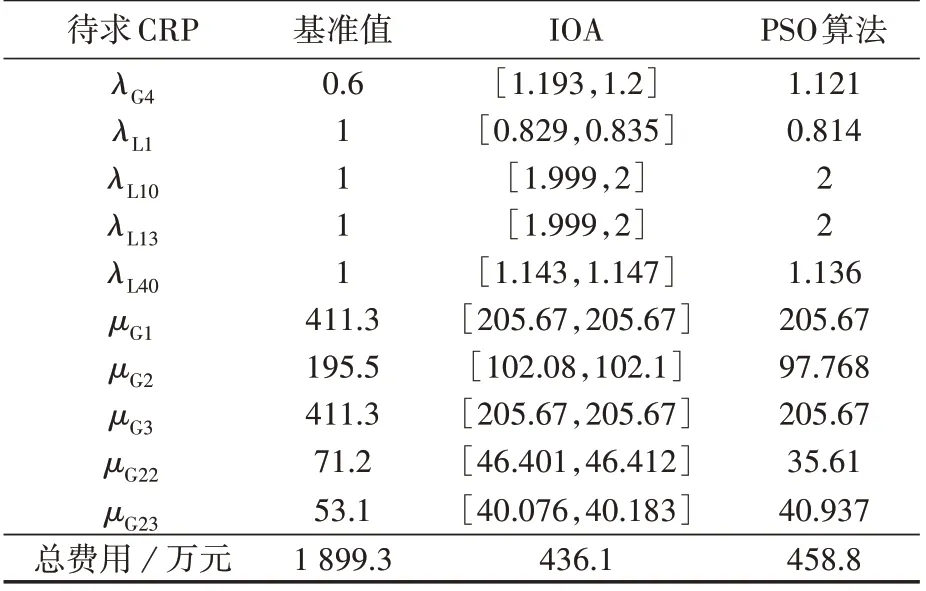
表8 P2下不同算法的可靠性参数求取结果（CS系统)Table 8 Results of reliability parameters with different algorithms under P2（CS system）

由表8得到的结论与表7相似，即在给定的可靠性参数优化模型以及经济性参数下，存在比基准可靠性参数取值及对应的基准费用更优的可靠性参数取值组合，且IOA得到的投资费用结果要好于PSO算法。

6.3 改进IOA的计算效率

基于IEEE-RTS系统测试改进IOA，量化分别采用Gauss-Seidel技巧改造和HC时的IOA效率，使用的指标包括收敛时的区间分割次数、区间评估次数等，其中区间评估次数为区间算子的求取次数。

表9给出了Gauss-Seidel技巧改进后对IOA性能的影响，表中，K-Newton指区间Krawczyk算子，H-Newton指改造后的区间Krawczyk-Hansen算子，区间范围［0.5，1.6］指待求CRP的区间上、下限分别设置为其真值的50 % 和其真值的1.6倍，区间范围［0.8，1.3］含义类似。当待求CRP个数为3时，利用的可靠性指标为系统LOLP、LOLF和EENS指标；当待求CRP个数为6时，利用的可靠性指标为节点15、节点18、系统各自的LOLF和EENS指标。

表9 Gauss-Seidel技巧改进对IOA性能的影响Table 9 Effect of Gauss-Seidel strategy improvement on performance of IOA

由表9可见，Gauss-Seidel技巧可小幅提升IOA的计算效率。表10给出了应用HC对IOA的影响。

由表10可见，相比区间H-Newton算法，使用HC可进一步降低算法的区间评估次数。

表10 HC对IOA性能的影响Table 10 Effect of HC on performance of IOA

然后，以RTS系统为例，分析算法计算效率的影响因素。利用的可靠性指标为节点15、节点18、系统的LOLF和EENS指标。表11给出了在不同的待求参数组合及参数的取值范围下，IOA的求解时间、区间分割次数、评估次数等效率评价指标。

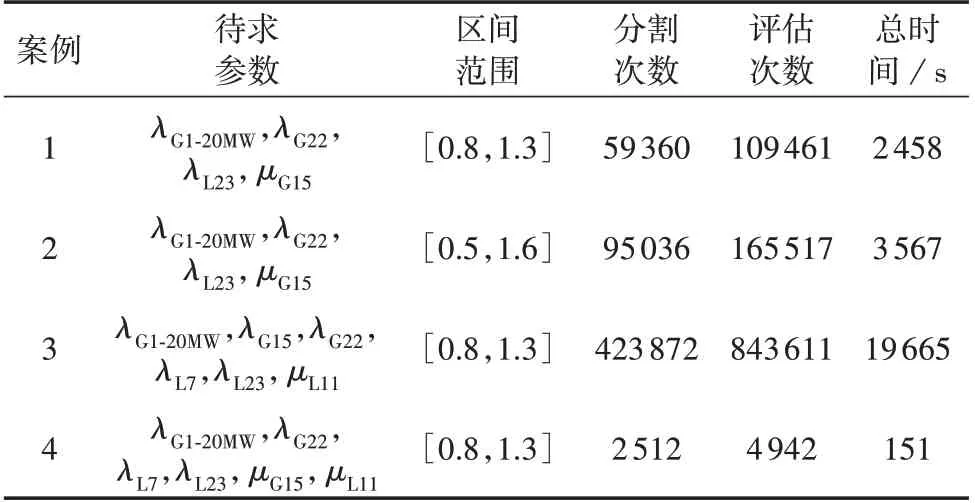
表11 不同条件下IOA的计算效率Table 11 Computation efficiency of IOA under different conditions

由表11中的案例1—3可知，通常区间分割次数、总时间等指标随着待求参数个数和区间范围的增加会显著增长。另外，IOA的计算效率还与选择的待求参数有关。比较案例3和案例4可知，虽然它们待求参数的数量同为6个，但由于选取的待求参数不同，计算时间存在较大的差别。

7 结论

针对现有IPRE研究的不足，本文在现有工作的基础上，建立了IPRE的一般性模型。针对逆问题的3种基本情形，分别采用相应的改进IOA求解。基于RBTS、IEEE-RTS和91节点系统测试了模型和算法在逆问题的不同情形下的有效性，并得出如下的结论。

1）根据待求可靠性参数个数与已知可靠性指标个数的大小关系、解的个数等，需要选用不同的逆问题模型和求解算法。

2）求解结果表明，相比常规非线性优化算法和PSO算法，IOA在逆问题的各种情形下均能求得参数的准确取值或者取得最优的解。使用常规优化算法时，一部分元件（如某些输电支路）可靠性参数的误差较大。

IPRE拓展和完善了传统可靠性评估理论，具有重要研究意义。当前，逆问题理论尚处于起步阶段，在其模型、方法和应用上仍需要系统深入的研究。例如：为更贴近工程实际，在可靠性参数补全和校正问题的研究中，下一步可计入可靠性指标统计值的误差；本文利用的是可靠性指标的统计均值，后续研究还可根据可靠性指标统计数据的概率分布信息求取元件参数的置信区间或概率分布。

附录见本刊网络版（http：//www.epae.cn）。