基于动态无功电压灵敏度的有源配电网移动式储能优化调度

王育飞，陈 强，郑云平，薛 花，李 明，米 阳

（1.上海电力大学 电气工程学院，上海 200090；2.国网新疆电力有限公司电力科学研究院，新疆 乌鲁木齐 830013）

0 引言

近年来，我国电量供需基本平衡，但区域性、时段性缺电现象仍然存在；分布式电源出力具有波动性和随机性，可能导致配电网出现“峰上加峰”现象，负荷峰谷差进一步加大［1］。同时，当分布式电源渗透率较高时，易造成系统电压发生偏差甚至越限［2-3］。移动式电池储能系统（mobile battery energy storage system，MBESS）兼具功率调节灵活性和时间-空间灵活性，为削峰填谷、电压质量等问题的解决提供了重要思路［4］。因此，研究MBESS在配电网中的优化调度具有重要的意义。

目前，国内外学者针对配电网中MBESS应用及调度的研究取得了一定的成果，且主要从MBESS有功出力的角度进行研究。文献［5］针对分布式电源带来的供需不平衡问题，提出了一种固定式储能和移动式储能的协调运行模型，以提高系统运行的经济性与可靠性，并采用自然聚集算法对模型进行求解。文献［6］以削峰填谷为优化目标，建立了双层优化调度模型，采用增强烟花算法（enhanced fireworks algorithm，EFWA）进行求解。文献［7］针对孤岛微电网构建了多目标优化模型，并提出了一种改进的偏好-激励协同进化算法。也有文献同时考虑MBESS的有功出力和无功出力，对MBESS的调度进行研究。文献［8］同时考虑MBESS参与削峰填谷和无功补偿，提出了一种日前优化调度模型，并采用改进粒子群优化算法进行求解。文献［9］以减小网损和调压为目标，提出了一种MBESS调度模型，并采用CPLEX求解器进行求解。文献［10］同时考虑利用MBESS进行峰谷差价套利、调压和最小化网损建立多目标模型，使配电网效益最大化，并提出了一种基于粒子群优化算法和混合整数凸规划的优化方法求解MBESS的调度方案。综上所述，在求解MBESS调度模型时，已有文献大多采用数学规划法、人工智能算法等，鲜有从电压灵敏度分析的角度进行研究。

电压灵敏度分析法已在光伏消纳能力［11-13］、储能选址定容［14］、电力系统稳定性［15-17］等研究领域获得较好的应用。制定MBESS调度方案的关键在于确定其功率补偿点与补偿量。配电网中的候选补偿点众多，若同时求解补偿点与补偿量，则易陷入维数灾难问题［18］。而采用灵敏度分析法先确定MBESS的有功和无功补偿点，可有效减少计算量。

对于配电网中已经配置的在常规情况下用于应急保电的MBESS而言，其在闲置时可用于削峰填谷。考虑到MBESS具备功率四象限运行能力，可同时吸收／发出有功功率和无功功率［19］，并能兼顾配电网调压，实现MBESS参与配电网调节的收益最大化，本文旨在通过无功电压灵敏度确定MBESS的最佳接入位置，从削峰填谷与改善配电网电压质量的角度分析MBESS的优化调度。MBESS的有功出力、无功出力与其接入位置存在耦合关系，无功电压灵敏度能够准确地反映注入无功功率后节点电压的变化。基于MBESS同时输出有功功率和无功功率，且有功和无功均会对节点电压产生影响，通过削峰填谷目标确定有功时序出力，从而计算满足仿射关系下的无功电压修正灵敏度；基于存在网络重构的配电网，并考虑不同时间下节点电压调整需求的不同，提出计及调压需求的动态综合无功电压修正灵敏度的计算方法。首先，构建了综合考虑MBESS运行经济性与可靠性的双层优化调度模型；其次，通过动态综合无功电压修正灵敏度计算MBESS的时序接入节点；然后，根据无功调压目标确定MBESS的无功时序出力；最后，确定MBESS的最优调度方案。

1 考虑MBESS功率四象限输出的有源配电网电压灵敏度分析

1.1 MBESS功率四象限输出特性

MBESS由载体和电池储能系统组成，其中电池储能系统变流器（power conversion system，PCS）通过双环控制器对输出的有功功率和无功功率进行解耦控制，实现储能系统输出功率的四象限运行。MBESS功率四象限输出范围如图1所示。图中：PMB，t为t时刻MBESS的有功出力，单位为kW；QMB，t为t时 刻MBESS的无功 出力，单位 为kvar；SMB为MBESS的额定视在功率。当PCS中的外环控制器检测到配电网存在有功功率和无功功率需求时，内环控制器控制电池储能的有功、无功出力大于0，此时电池储能向电网释放有功、无功功率，处于放电状态，对外进行无功补偿，相应的MBESS工作模式处于第一象限；当外环控制器检测到配电网中的有功功率和无功功率富余时，内环控制器控制电池储能的有功、无功出力小于0，此时电网向电池储能输送有功、无功功率，电池储能处于充电状态，从外界吸收无功功率，相应的MBESS工作模式处于第三象限；同理，MBESS也可工作于第二、四象限或坐标轴上，可根据实际需求灵活控制其充放电状态。

图1 MBESS功率四象限输出范围Fig.1 Power four-quadrant output range of MBESS

基于MBESS有功功率和无功功率的灵活调节能力，本文主要针对MBESS的有功出力参与削峰填谷、无功出力参与电压调节多应用场景下的优化调度进行研究。

1.2 有源配电网的电压灵敏度分析

1.2.1 基于仿射关系的无功电压修正灵敏度计算

对于含有N个节点的配电网而言，其节点电压幅值变化量ΔU与有功序列ΔP及无功序列ΔQ之间的关系满足：

式中：ΔUP为有功功率变化引起的节点电压幅值变化量；ΔUQ为无功功率变化引起的节点电压幅值变化量；αPV为有功电压灵敏度矩阵；βQV为无功电压灵敏度矩阵。式（1）的具体展开式如附录A式（A1）所示。

MBESS接入配电网提供服务，其有功功率和无功功率均会对节点电压造成影响。因此，在采用无功电压灵敏度确定MBESS的最佳接入节点时，应考虑有功出力对系统电压的影响。

MBESS的有功出力与无功出力具有相对独立性，可先确定其参与削峰填谷的有功出力，即式（1）中的ΔP。将αPV和ΔP的结果代入式（1）即可求得MBESS有功出力确定情况下的节点电压幅值变化量ΔUP，从而建立电压与注入有功功率和无功功率之间满足的仿射关系。进一步地，确定单位无功补偿量，补偿量的大小只会影响灵敏度值的大小，并不会影响灵敏度之间的大小关系。最后可计算得到相应的电压增量，修正后的无功电压灵敏度矩阵如式（2）所示。

式中：ΔU′为修正后的节点电压幅值变化量。

为了反映系统中节点j注入无功功率时该节点对系统整体电压的影响，可将βQV按列求和，用式（3）表示节点j注入无功功率时的静态综合无功电压修正灵敏度ZS，j。

式中：βij为节点j注入无功功率ΔQj后节点j对节点i的无功电压灵敏度。

1.2.2 计及网络重构的动态综合无功电压修正灵敏度分析

当MBESS的无功出力参与电压调节时，应根据各节点的实际调压需求进行调整。不同节点的电压偏离额定电压值的程度不同，因此引入电压偏差因子ωi对静态综合无功电压修正灵敏度进行改进，如式（4）所示。

式中：Vi、Vi，rate分别为节点i的实际电压值、额定电压值。

有源配电网中可能同时存在因分布式电源的接入导致的并网节点电压偏高、馈线末端电压偏低的情况。当利用MBESS对电压偏高节点的电压进行下调时，应避免造成电压偏低节点的电压发生恶化；当利用MBESS对电压偏低节点的电压进行上调时，应避免造成电压偏高节点的电压发生恶化。因此，考虑对电压偏高节点和电压偏低节点进行分类，对静态综合无功电压灵敏度进行改进，如式（5）所示。

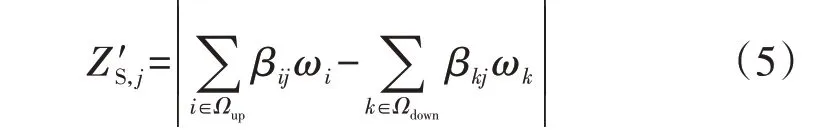
式中：Z′S，j为改进后节点j的静态综合无功电压灵敏度；Ωup、Ωdown分别为实际电压值高于、低于额定电压值的节点集合。

在有源配电网中，有时为了缓解分布式电源所带来的线路阻塞及电压质量问题，会对配电系统进行网络重构。若网络拓扑结构发生改变，则整个系统的节点电压分布规律也随之改变。考虑网络重构与不同分布式电源出力情况下各节点的电压情况，结合MBESS的时间-空间灵活性，将上述改进的静态综合无功电压修正灵敏度推广至动态综合无功电压修正灵敏度，对调度周期内各个时刻的无功电压灵敏度Z′S，j，t进行计算，如式（6）所示。

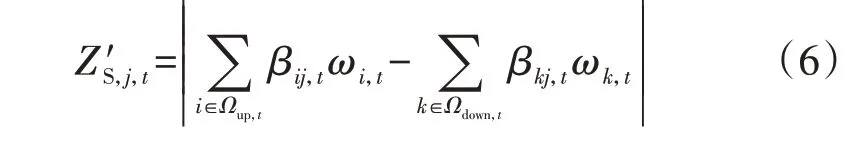
式中：Ωup，t、Ωdown，t分别为t时刻实际电压值高于、低于额定电压值的节点集合；βij，t、βkj，t分别为t时刻节点j注入无功功率ΔQj后节点j对节点i、节点k的无功电压灵敏度；ωi，t、ωk，t分别为t时刻节点i、节点k的电压偏差因子。

2 MBESS双层优化调度模型

2.1 外层经济运行模型

外层优化模型以MBESS的日净收益最大化为目标，以配电网内允许安装的MBESS容量约束、节点电压约束、线路功率约束及系统功率平衡约束为约束条件，决策变量为MBESS的时序有功出力序列。

2.1.1 目标函数

外层优化模型的目标函数可表示为：

式中：F为MBESS的日净收益；Ca为低储高放套利收益；Cd为折合到每天的延迟电网升级收益；Cl为日降损收益；CMBESS，inv、CMBESS，o&m分别为MBESS折合到每天的 投 资 成 本、日 运 维 成 本；Ce，t为t时 刻 的 电 价；PMBESS，h，t为t时 刻MBESSh的有功 出力，为正值 表示MBESSh向电网释放电能，为负值表示MBESSh从电网吸收电能；Tlife为MBESS的等效运行年限；Cexp为电网的升级成本；rinf、rdis分别为通货膨胀率、贴现率；τ、ξ分别为MBESS的削峰率、负荷年增长率；Ploss，t、PMBESS，loss，t分别为MBESS接入前、后t时刻系统的有功 功 率 损 耗；Ctruck，h为MBESSh的 卡 车 成 本；EESS，h、PESS，h分别为MBESSh的额定容量、额定功率；CE、CP分别为储能系统的单位容量、单位功率投资成本；H为每天调度的MBESS数量；Clabor为每辆卡车每天的驾驶员人力成本；Cm为MBESS的单位功率维护成本。

我们国家存在收入不均问题，这样也能够看出，个人所得税的改革是存在一些问题的，我国的社会主义市场经济和广大人民群众的生活现状就是工薪阶层的福利待遇比较少，并且物价持续增加，低收入人员存在经济困难的问题。因此需要降低个人所得税征收额，或者是对于那些低收入的人员，采取免缴的工作调整措施，增加福利，降低免征额，这样可以起到更加显著的效果。

2.1.2 约束条件

1）配电网内允许安装的MBESS容量约束。

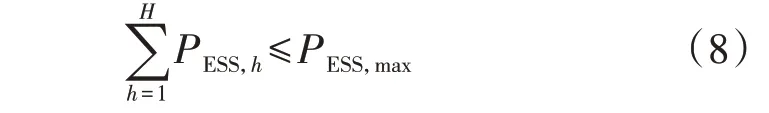
式 中：PESS，max为 配 电 网 内 允 许MBESS接 入 的 最 大容量。

2）节点电压约束。

式中：Vi，t为t时刻节点i的电压幅值；Vi，max、Vi，min分别为节点i电压的上、下限。

3）线路功率约束。

式中：Sl，t为t时刻线路l的传输功率；Sl，max为线路l所允许传输功率的最大值。

4）系统功率平衡约束。式中：Pgrid，t、PDG，t、Pload，t分别 为t时刻 的 网供有功 功率、分布式电源有功出力、负荷有功功率；Qgrid，t、QDG，t、Qload，t分 别 为t时 刻 的 网 供 无 功 功 率、分 布 式电 源 无 功 出 力、负 荷 无 功 功 率；QMBESS，h，t为t时 刻MBESSh的无功出力；QMBESS，loss，t为MBESS接入后t时刻系统的无功功率损耗。

2.2 内层时序优化模型

内层优化模型以等效负荷标准差最小化和各时刻的整体电压偏移最小化为目标，以MBESS功率约束、荷电状态约束、运行状态约束为约束条件，决策变量为MBESS的接入节点及时序无功出力序列。

1）削峰填谷目标函数。

内层考虑MBESS的有功出力调节能力，MBESS既可以作为电源向电网供电，降低负荷曲线的高峰，也可以作为负荷从电网吸收电能，抬高负荷曲线的低谷。因此，选取等效负荷标准差最小化作为内层削峰填谷的目标函数，如式（12）所示。

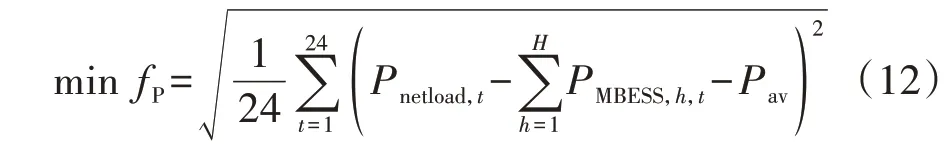
式中：fP为等效负荷标准差；Pnetload，t为t时刻的等效负荷；Pav为MBESS接入配电网后整个调度周期内等效负荷的平均值。

2）无功调压目标函数。

为了定量反映MBESS接入对系统电压水平的提升能力，引入能反映t时刻节点i电压质量的馈线电压指标IVQ，i，t，以各时刻整体电压偏移最小化作为无功调压的目标函数，如式（13）所示。

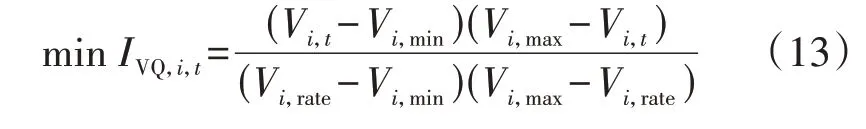
2.2.2 约束条件

假设MBESSh的接入位置已根据改进的无功电压灵敏度确定，则接入节点i处的MBESS在t时刻的出力应满足以下约束条件。

1）MBESS功率约束。

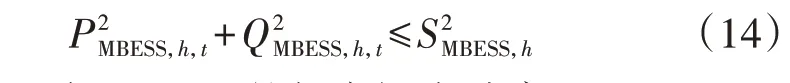
式中：SMBESS，h为MBESSh的额定视在功率。

2）荷电状态约束。

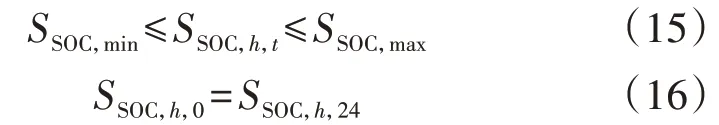
式 中：SSOC，h，t为t时 刻MBESSh的 荷 电 状 态；SSOC，max、SSOC，min分别为MBESS荷电状态的上、下限值；SSOC，h，0、SSOC，h，24分别为调度 周 期 始、末时刻MBESSh的荷 电状态。

3）运行状态约束。式中：μc，h，t、μd，h，t分别为t时刻MBESSh的充电、放电状态标志变量，MBESSh处于充电状态时有μc，h，t= 1、μd，h，t= 0，MBESSh处于放电状态时有μc，h，t= 0、μd，h，t= 1，MBESSh处于浮充状态或移动状态时有μc，h，t=μd，h，t= 0。

3 求解方法及流程

MBESS的调度问题具有高维、非线性特性，根据动态综合无功电压修正灵敏度确定不同时刻MBESS的接入节点，可避免采用优化算法对配电网中可接入的节点进行编码，能有效降低编码维度。

本文采用双层优化方法对MBESS的调度问题进行循环反馈优化。首先，基于上述灵敏度计算结果，选择各时刻灵敏度最大的节点作为MBESS的接入节点。然后，根据多应用场景对MBESS的时序有功、无功出力进行编码，采用EFWA进行求解。EFWA在前期具有较强的全局搜索能力，在中后期具有较强的局部搜索能力，可避免传统智能算法求解该类问题易陷入局部最优解的困扰。其中，设定利用MBESS无功出力进行调压的目标为最小化各时刻配电系统的节点电压偏移，找到可行解即跳出循环寻优过程。最后，将所得MBESS的时序无功出力序列反馈至外层模型。

为了方便潮流计算，引入式（18）所示网络邻接矩阵M表征配电网中各节点之间的联络状态。

式中：第i行第j列元素表示节点i与节点j之间是否有线路连接，若有则取值为1，否则取值为0。

若接入配电网的MBESS数量大于1，则将MBESS依次并入电网，后接入的MBESS在已接入MBESS的基础上更新等效负荷数据并重新计算灵敏度。

综上，MBESS双层优化调度模型的求解流程图如图2所示，具体求解步骤见附录B。

图2 MBESS双层优化调度模型的求解流程图Fig.2 Flowchart of solving two-layer optimal scheduling model of MBESS

4 算例仿真分析

4.1 算例数据

为了适应网架结构发生变化的应用场景，本文选用进行网络重构的配电网验证所提方法的有效性。以IEEE 33节点配电系统为例，其结构见附录C图C1，并采用文献［20］中的网络重构方案及日前负荷、光伏发电和风电数据进行仿真分析，相关仿真参数见附录C表C1。配电网在00:00—07:00、07:00—16:00、16:00—24:00这3个时段的开断线路分别为“l7、l9、l14、l28、l31”“l7、l9、l30、l33、l37”“l8、l30、l33、l35、l37”。

系统的额定电压为12.66 kV，分别在节点9和节点32处接入额定容量为2.0、0.4 MW的光伏，分别在节点15和节点26处接入容量为0.5、1.5 MW的风机。风电、光伏发电及负荷日前预测曲线见附录C图C2。各时段的电价见附录C表C2。假设配电网中已配置2个常规情况下用于应急保电的MBESS（MBESS1和MBESS2），在闲置时可将其用于削峰填谷，同时兼顾配电网调压，其参数见附录C表C3。

4.2 仿真结果分析

4.2.1 基于灵敏度选择接入节点结果分析

首先，通过潮流计算获得各节点的时序电压值，根据电压情况分别计算传统综合无功电压灵敏度和综合无功电压修正灵敏度。为了验证本文所提灵敏度计算方法的有效性，选取15:00时刻的综合无功电压灵敏度（标幺值）进行对比分析，结果如图3和附录C表C4所示。在15:00时刻的网络结构下，节点30与节点31之间的线路处于断开状态，两节点均处于各自馈线支路的末端。由于此时节点32处的光伏出力较大，节点31的电压值已接近额定电压值，基本不需要进行调压。而节点30的电压值已接近下限值，应对该节点的电压进行上调，故MBESS更适合选择节点30作为此时的接入节点。

图3 15:00时刻的综合无功电压灵敏度对比Fig.3 Comparison of comprehensive reactive power and voltage sensitivity at 15:00

若按照传统综合无功电压灵敏度的计算结果选择MBESS接入节点，则在15:00时刻应选择节点31；而若考虑各节点的实际电压情况及MBESS的有功出力，即采用本文所提灵敏度计算方法，则在15:00时刻选择节点30作为MBESS的最佳接入节点更合适。

4.2.2 MBESS的调度结果分析

采用本文所提灵敏度计算方法计算全天24 h的时序灵敏度，并对各时刻的灵敏度进行排序，选取各时刻灵敏度最大的节点作为MBESS的最佳接入节点。

由于未考虑各节点间的实际距离，假设MBESS能在1 h内完成任意两节点间的移动和安装。2个MBESS的调度方案如表1所示。由表可以看出，根据各时刻网络结构及各节点电压情况的不同，2个MBESS在不同时段根据灵敏度计算结果所得的最佳接入节点也不同。2个MBESS的时序有功和无功出力结果如图4所示。MBESS的削峰填谷效果如图5所示。由图5可以看出，通过MBESS吸收或注入有功功率，净负荷曲线的峰谷差得到明显减小。

图4 MBESS的时序有功和无功出力Fig.4 Sequential active and reactive output of MBESSs

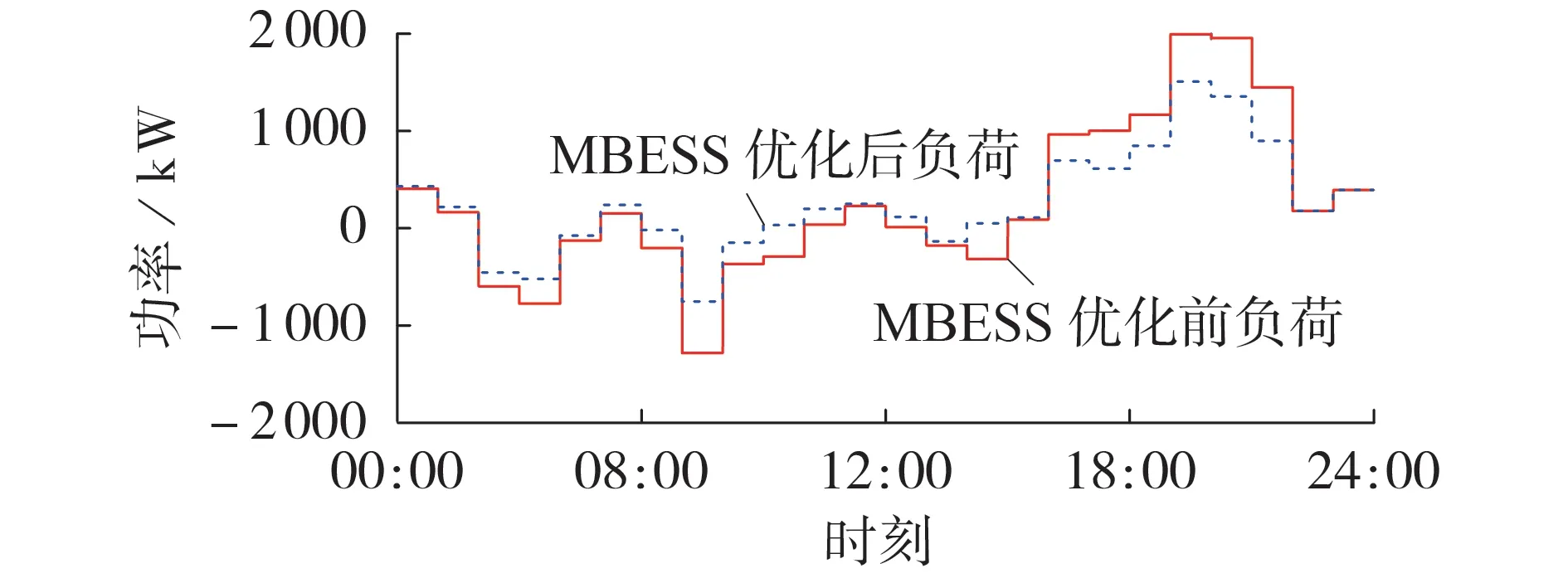
图5 MBESS的削峰填谷效果Fig.5 Peak load shifting effect of MBESS

表1 MBESS的调度方案Table 1 Scheduling scheme of MBESSs

为了验证EFWA的优越性，将其与粒子群优化算法、CPLEX求解器进行对比分析，结果如表2所示（表中节点电压范围为标幺值）。由表可知：采用粒子群优化算法进行求解时，负荷峰谷差减小为2 393 kW，相比优化前负荷峰谷差率降低了27 %，系统网损减少了117 kW，MBESS日净收益为174元；采用CPLEX求解器进行求解时，负荷峰谷差减小为2 441 kW，相比优化前负荷峰谷差率降低了25.5 %，系统网损减少了59 kW，MBESS日净收益为167元；采用EFWA进行求解时，负荷峰谷差减小为2 261 kW，相较于优化前负荷峰谷差率降低了31 %，系统网损减少了210 kW，MBESS日净收益为198元；3种优化方法均能使全时段系统节点电压保持在允许的合理范围内，满足配电网的调压要求。

表2 不同优化方法的求解结果对比Table 2 Comparison of solution results among different optimization methods

通过上述对比分析可知，EFWA在削峰填谷效果、减少系统网损及MBESS日净收益3个维度的求解结果都更优于粒子群优化算法和CPLEX求解器方法，其在求解MBESS优化调度问题时具有优越性。

MBESS提供无功出力后全时段系统的节点电压（标幺值）如图6所示。可以看出，MBESS通过在不同时间对不同节点进行无功补偿，使系统整体电压全时段都保持在0.95～1.05 p.u.范围内，且电压分布较为均匀，有效减少了总体电压偏移。

图6 MBESS接入后各节点电压Fig.6 Voltage of each bus after access of MBESS

计算MBESS的经济效益，结果见表3。可看出，优化MBESS的调度方案后，MBESS可获得的日净收益为198元。此外，MBESS的无功调压具有隐性价值，但由于目前的电力市场机制不够完善且缺乏政策支持，本文暂未考虑该部分收益。

表3 MBESS的经济性分析Table 3 Economic analysis of MBESS

5 结论

为了应对分布式电源接入配电网带来的负荷峰谷差过大和电压质量问题，本文提出了一种基于动态综合无功电压修正灵敏度分析的优化调度方法。针对传统电压灵敏度在有源配电网中适用性不足的问题，综合考虑MBESS的有功、无功出力对系统节点电压的耦合影响以及不同网络结构下各节点电压的调压需求，提出了满足仿射关系的动态综合无功电压修正灵敏度的计算方法，并采用EFWA求解所提双层优化调度模型。算例仿真结果表明，采用所提电压灵敏度计算方法确定MBESS的调度方案，能在保证经济性的前提下，有效地减小负荷峰谷差，提升系统的整体电压水平。

附录见本刊网络版（http：//www.epae.cn）。