一种新型双向三电平倍流LCL-T谐振直流变换器

张钟艺，金 涛，肖晓森，戴向阳，吴维鑫

（1.福州大学 电气工程与自动化学院，福建 福州 350108；2.福州大学 福建省新能源发电与电能变换重点实验室，福建 福州 350108）

0 引言

随着以电动汽车为代表的新能源产业的发展，对车载充电机（on-board charger，OBC）［1］的性能提出了更高的要求。为了拓展OBC功能与运用场合，将以往传统的单向式功率传输改变为双向式功率传输［2-3］。近年来，双向OBC大多数采用电压源DC-DC变换器，特别是LLC谐振拓扑［4-5］，因能实现宽负载范围内的开关管零电压开通（zero voltage switching，ZVS）和整流二极管的零电流关断（zero current switching，ZCS），提高变换器运行效率，从而得到越来越多的关注与应用。

此外，由于恒流充电方式［6］具有能够根据电池容量计算出充电电流值与充电时间的优势，目前被广泛应用在新一代车载蓄能锂电池荷电状态（state of charge，SOC）智能管理上。但随着恒流充电的进行，锂电池内阻将不断增加，而传统的电压源型变换器并不存在自然的恒流输出特性，因此需要具备较宽的电压增益调节范围。而LLC谐振拓扑普遍采用脉冲频率调制进行电压增益控制［7］，这将导致必须通过较大的开关频率变化来拓宽电压增益调节范围，额外提高了谐振腔磁性元件设计难度且会产生电磁干扰问题［8］。文献［9-10］则提出了一类基于输入串联输出并联（input series and output parallel，ISOP）系统的谐振直流变换器，通过高频隔离变压器，使2个LLC／CLLC谐振模块ISOP，以此来获得可变电流增益，但要求实际器件差异较小，同时还需设计辅助结构或特定控制，才能实现各模块较好的均流。

对于单向LCL-T谐振拓扑［11-13］，当变换器运行在归一化频率fn= 1时，输出电流将与负载无关［14-15］，无需额外控制就可形成自然的恒流输出特性，同时还令电感比λ＜1来实现开关管ZVS［16］。但双向LCL-T谐振拓扑势必要求λ=1，即利用谐振腔参数对称设计，实现变换器双向功率传输特性相一致。文献［17-18］介绍了一种LCL-T谐振型双有源桥双向DC-DC变换器，采用双移相控制方式，通过调节初、次级全桥交流侧电压相位与电流相位关系以维持恒流输出，并产生一定量的无功功率，进而实现开关管ZVS。但无功功率将降低恒流输出精度与变换器运行效率，且控制方式受全桥结构的严格约束。此外，为使开关管能够适应高压输入的场合，三电平中性点箝位（three-level neutral-point clamp，3L-NPC）脉冲宽度调制变换器［19］应运而生，在实现开关管ZVS的基础上，使得开关管耐压降至输入电压的一半［20］。并且，为实现不同电压等级的车辆之间的功率传输，要求变换器具备可变电流增益的恒流充电功能。

综上，本文将LCL-T谐振结合三电平级联中性点箝位（three-level cascaded neutral-point clamp，3L-CNPC）有源桥，提出了一种新型双向三电平倍流LCL-T谐振直流变换器。其由谐振腔输入、输出端口分别连接一个3L-CNPC有源桥构成，而3L-CNPC有源桥是借鉴文献［12-13］的ISOP思想，由2个3LNPC桥臂直流侧并联，交流侧通过耦合变压器级联来构成，并通过其箝位作用实现各桥臂自均流。由于耦合变压器级联的特殊方式，有源桥各子桥臂可独立或并行工作，据此设计不同的调制方式控制谐振腔输入电压，建立变换器一倍、二倍准恒流（quasiconstant-current，QCC）模式。同时为了克服文献［17-18］中双移相控制增加额外开关损耗的缺点，在实现双向功率传输特性一致、谐振腔器件参数对称设计的前提下，借鉴传统单向谐振变换器基波分析法建模，进而研究了一种受归一化频率fn、品质因数Q控制的LCL-T谐振准恒流输出，并考虑无功功率控制和实现开关管ZVS，设计满足给定准恒流输出精度的输出工况筛选算法。

1 各模式工况暂态分析

1.1 拓扑结构

图1为本文所提新型变换器的拓扑结构，其由输入端口（电压为Uinp、Uins）、分压电容（C1p、C2p、C1s、C2s）、3L-CNPC有源桥与LCL-T谐振腔模块（resonant tank module，RTM）组成。3L-CNPC有源桥由3LNPC主桥臂（main bridge arm，MBA）与3L-NPC辅助臂（auxiliary bridge arm，ABA）在直流侧并联，在交流侧通过匝比固定为1的耦合变压器TXp（TXs）级联所构成，且分布在RTM两侧（左侧为LMBA、LABA，右侧为RMBA、RABA），形成对称的变换器拓扑电路。Q1—Q4、T1—T4为MBA开关管，Q5—Q8、T5—T8为ABA开关管，D1—D8、DT1—DT8为开关管体二极管，C1—C8、CT1—CT8为开关管寄生电容，Dj1、Dj2（j=1，2，3，4）为箝位二极管，Cf1—Cf4为飞跨电容。RTM由谐振电感Lr、谐振电容Cr、漏感Lk与匝比为k的隔离变压器TX构成。

图1 本文所提新型变换器的拓扑结构Fig.1 Topology structure of proposed novel converter

左侧有源桥中，LABA输出端口电压为umo，LMBA输出端口电压（即RTM输入电压）为uab=uao+uob，其中uao为LMBA输出电压，uob为TXp副边输出电压，且由于TXp耦合作用，umo=uob，则uab=uao+umo。同理，右侧有源桥中，RMBA输出端口电压为ucd=uco′+uho′，其中uco′为RMBA输出电压，uho′为RABA输出电压。此外，uao′与umo′的输出控制相互独立。

各模式工作暂态分析一律基于以下几点原则：①功率从左传输到右，且右侧有源桥输入源端口等效为负载电阻RL，变换器输出电压即为Uins，输出电流即为iins；②开关管和二极管均为理想器件，导通电阻为0，开关管寄生电容大小均等于Coss；③TXp、TXs均为理想变压器，严格遵守匝比规律，可忽略励磁电流；④分压电容C1p、C2p和C1s、C2s分别能够理想均分Uinp和Uins；⑤飞跨电容Cf1—Cf4间无器件差异。

1.2 一倍准恒流模式工况

一倍准恒流模式所采用的调制方式为：RTM右侧有源桥所有开关管常闭，LABA中Q5、Q8常闭而Q6、Q7常开，使得TXp被短路，则umo=uob=0，进而uab=uao。同时，为实现开关管ZVS，在［t1，t4］时段LMBA采用固定最小移相角α的方式，形成超前管Q1、Q4与滞后管Q2、Q3。一倍准恒流模式下开关管驱动信号及关键参数波形如附录A图A1所示。在此基础上，得到上半工作周期（［t0，t8］）各开关模态电路如附录A图A2所示，且其对应各暂态分析如下。

开关模态0（［t0，t1））：根据谐振电流ip环路，ip将持续对Cr充电，使得谐振电容电压uCr大于RTM输出电压um，导致RTM输出电流is1不断上升。该过程中，uao被C1p箝位至Uinp/2，则uab=Uinp/2。此外TXs耦合作用形成is=iTXs，其中is为is1折算至TX副边整流电流，iTXs为TXs副边耦合电流，则根据is与iTXs环路，uho′、uco′均被C1s箝位至Uins/2，使得ucd=Uins，即um=kUins。

开关模态1（［t1，t2））：在t1时刻关断Q1，ip立即对C1充电，同时C4通过Cf1、C2p回路放电，构成LMBA超前管ZVS换流过程。该过程使uao由Uinp/2逐渐降为0。但因死区时间较短，ip近似不变，故RTM右侧有源桥暂态过程不变。

开关模态2（［t2，t4））：在t2时刻，C1电压一旦升至Uinp/2，立即被D11箝位，同时C4电压也降至0，并导通D4，则换流过程结束。ip经C2p、D4、Cf1与Q2续流，uab=0。在t3时刻，导通Q4实现ZVS。但由于ip仍对Cr充电，维持uCr＞um，导致ip将逐渐减小。

开关模态3（［t4，t5））：在t4时刻关断Q2，ip立即对C2充电，同时C3放电，构成LMBA滞后管ZVS换流过程。uao由0逐渐降为-Uinp/2。但受ip减小的影响，关断电流随之减小，尽管本阶段中，ip极性未变，但滞后管较之超前管更难实现ZVS。

开关模态4（［t5，t6））：在t5时刻，C2电压升至Uinp/2，C3电压降至0，并导通D3，则换流过程结束。同时刻导通Q3实现ZVS，uao被C2p箝位至-Uinp/2，则uab=-Uinp/2，使得ip过零点并反向增大。为维持ip与is1，Cr开始放电，导致uCr下降。当uCr=um时，is1达到正极性峰值，此后，随着uCr＜um，is1将不断下降。

开关模态5（［t6，t7））：在t6时刻，uCr降至-kUins，is1过零点，使得is均分两路，一路对CT1、CT2和CT5、CT6充电，另一路使CT3、CT4和CT7、CT8放电，构成RMBA和RABA中体二极管ZCS换流过程。同时，ucd将随着换流过程的进行由Uins逐渐下降至-Uins，也即um由kUins逐渐下降至-kUins。根据图A2（f）可列出如下节点电流方程组：

式中：iC1s为流经分压电容C1s的电流；iCT1、iCT4、iCT5、iCT8分别为流经开关管寄生电容CT1、CT4、CT5、CT8的电流。由式（1）中后四式可得iCT5=iCT8=iCT1=iCT4=is/2，代入第三式中可得iins=is，表明ZCS换流过程并不会增加额外的电能损耗。

开关模态6（［t7，t8］）：在t7时刻，ZCS换流过程结束，CT3、CT4和CT7、CT8的电压降至0，DT3、DT4和DT7、DT8被导通以实现ZCS。再根据is与iTXs环路，可得iins=is，同时uho、uco均被C2s箝位至-Uins/2，则ucd= -Uins，即um= -kUins。又由于uCr＜um，ip持续对Cr反向充电，则is1不断反向增大，变换器开始进入下半工作周期。

根据上述暂态分析，输出uab为三电平，即Uinp/2、0和-Uinp/2。同时在变换器全工作周期中，iins恒为is，因此右侧有源桥可完全等效视为全桥整流电路。

1.3 二倍准恒流模式工况

不同于一倍准恒流模式，LABA将采用与LMBA相同的调制方式，RTM右侧有源桥所有开关管仍然常闭，但变换器输入端口电压由Uinp降为Uinp/2，形成二倍准恒流模式。该模式下uab=uao+umo=2uao=2umo，输出uab的三电平仍为Uinp/2、0和-Uinp/2，则输出ip近似于一倍准恒流模式。因此，二倍准恒流模式下开关管驱动信号及关键参数波形与一倍准恒流模式基本相同。其上半工作周期开关模态0电路如附录A图A3所示。LABA中开关管Q5、Q6导通，TXp原边电流iTXp从m点流出，经TXp原边、o点、C1p和Q5、Q6回流入m点。而ip环路可参考一倍准恒流模式。另依靠TXp箝位作用实现自均流，则ip=iTXp。根据本模态电流环路，uao、umo均又被C1p箝位至Uinp/4，则uab=2umo=2uao=Uinp/2。

后续二倍准恒流模式开关模态暂态分析均可参照一倍准恒流模式。由于二倍准恒流模式下is1和is的暂态过程均无异于一倍准恒流模式，右侧有源桥也可等效视为全桥整流电路。

2 LCL-T谐振准恒流输出特性研究

2.1 LCL-T谐振恒流特性分析

通过基波分析法建立变换器交流等效运算电路，如图2所示。图中：ufund、uo、ip、is1分别为uab、um、ip、is1基波矢量；ωs=2πfs，为开关角频率，fs为开关频率；Req为负载电阻RL的交流等效电阻，表达式见式（2）。

在一、二倍准恒流模式下，uab输出方波电压幅值Uab=Uinp/2，um输出方波电压幅值Um恒为kUins。建立基波矢量峰值Ufund.p、Uo.p与Uab、Um的转换关系，如式（3）所示。

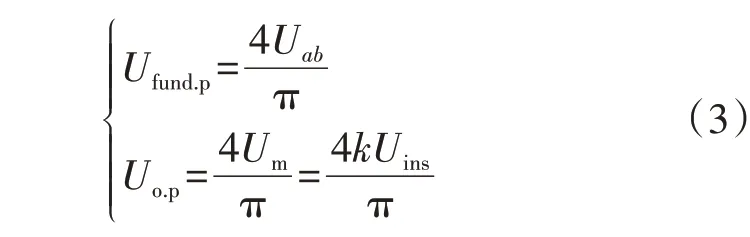
另定义LCL-T谐振腔谐振频率fr、归一化频率fn、特征阻抗Zn、品质因数Q和谐振电感比λ，表达式为：

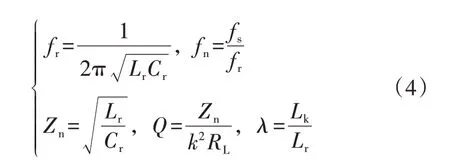
再根据图2并结合式（2）—（4），变换器一倍准恒流模式下电压增益M1与电流增益H1均可以化简为以fn、λ、Q为自变量的函数表达式，分别见式（5）、（6）。

式中：iinp=Uab/Zn，为额定输入电流。

式中：θ为谐振腔输入阻抗Zin阻抗角。

由于ip=ufund/Zin，ip初始相位φ=-θ。根据式（9），只有当fn=1，λ＜1时，才能使得φ＜0。但为保障变换器双向功率传输特性一致，λ需恒等于1。为此，固定λ=1，研究无功功率控制和实现开关管ZVS受fn、Q影响的规律，并以此作为限制条件，筛选特定的变换器输出工况，以实现一种受fn、Q控制的LCL-T谐振准恒流给定精度输出。

2.2 变换器无功功率控制和实现开关管ZVS

根据：

则无功功率传输效率η为：

有功功率传输效率ηp为：

再根据式（10），ip时域表达式为：

则超前管关断时刻电流大小为：

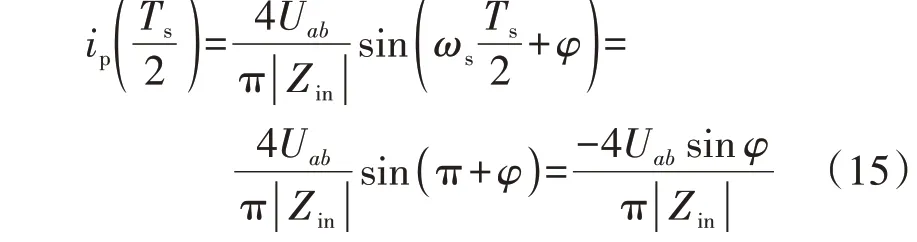
式中：Ts为开关周期。

由于超前管死区时间tDTb（即图A1中［t1，t3））一般极短，可视ip恒定，则利用电荷守恒原理来设计tDTb。一倍准恒流模式下，建立如下不等式：

式中：uds为开关管耐压。则tDTb取值范围为：

滞后管死区时间tDTL（即图A1中［t4，t5））在tDTb基础上适当加大。另结合图A1可建立如下不等式：

则根据式（17）、（18），建立实现开关管ZVS的不等式为：

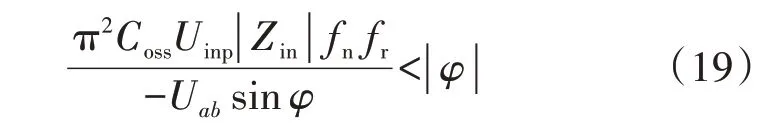
基于式（8）、（19），建立如下函数：

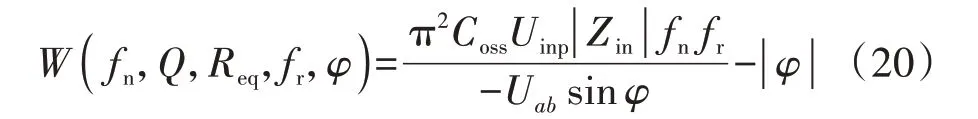
又根据式（2）、（4）可得：

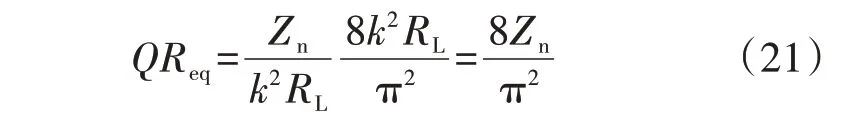
将式（21）代入式（8）消除Req，则函数W(fn，Q，Req，fr，φ)可被转化为函数w(fn，Q，Zn，fr，φ)，表达式为：

2.3 LCL-T谐振准恒流输出工况设计方法

给定一倍准恒流模式输入工况为：Uinp=200 V，iinp=1.76 A，fr= 45 kHz，Coss=480 pF（基于Saber平台IRF460器件MASK模型）。则Zn=Uab/iinp=56.8 Ω，进而可得Cr=1/（2πZnfr）=62 nF，Lr=Z2nCr=200 μH=Lk。

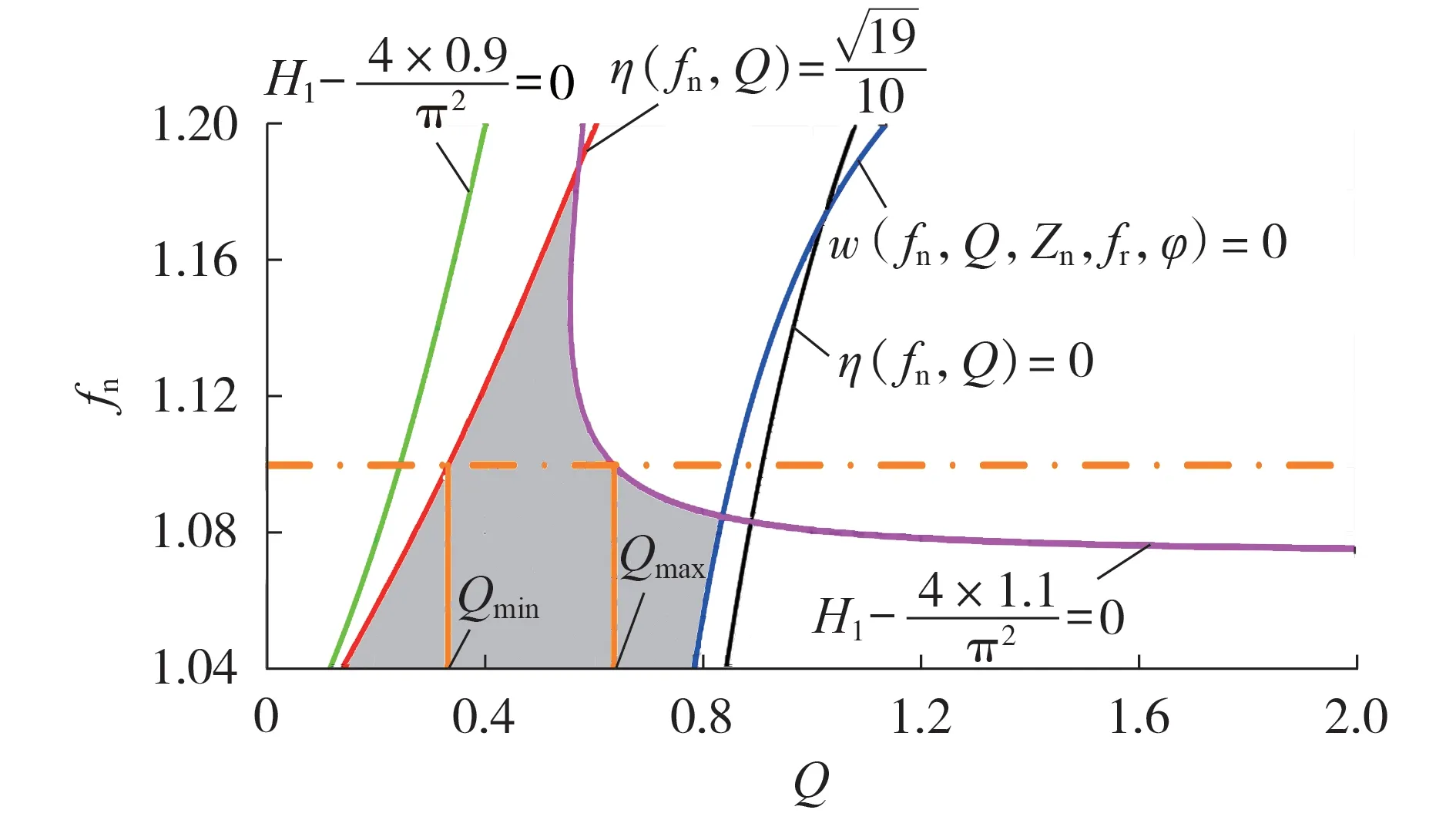
图3 各隐函数曲线图Fig.3 Graphs of implicit functions

图3中阴影区域即为满足各限制条件的fn、Q取值区域。但这些条件还不能完全阐释准恒流输出特性。必须要具备在窄电流增益变化下实现宽电压增益变化的能力，使准恒流输出特性更加接近自然的恒流输出特性。图3中，随着fn值大小的变化，与阴影区域边界相交可得Qmax、Qmin，再代入H1与M1表达式中，计算出H1max、H1min与M1max、M1min。基于这些计算值，制定一套准恒流输出工况筛选算法，输出满足H1与M1给定限制范围的fn、Qmax和Qmin，其流程图如附录A图A4所示。

再根据已给定的fr、Zn，计算出一倍准恒流模式输出工况：fs=fnfr，最大负载电阻RLmax=Zn/Qmin，最小负载电阻RLmin=Zn/Qmax。而二倍准恒流模式输出工况则在不改变Lr、Cr和Lk的基础上，保持与一倍准恒流模式输出工况相同即可。

3 仿真验证与分析

3.1 仿真参数设计

根据第2节分析，通过筛选算法可以得到：fn=1.1，Qmax=0.63，Qmin=0.34，H1max-H1min=4.125 %＜10 %，M1max/M1min=168.14 %＞160 %。则一倍准恒流模式输出工况为：fs=50 kHz，RLmax=167.06 Ω，RLmin=90.16 Ω。结合2.3节给定的输入工况，其余额定及仿真参数如附录A表A1所示。仿真结果中输出电压、输出电流变量下标中的1、2分别代表一倍、二倍准恒流模式。

3.2 一倍准恒流模式仿真分析

根据式（18），可 得tDTb＜ |φ|（/4πfs）=0.15（/4π×50 000）≈0.24 μs。为更好地实现超前管与滞后管ZVS，适当增大tDTb，取tDTb=0.25 μs、tDTL=0.25 μs。又令α=tDTb·2πfs=π/40。一倍准恒流模式仿真结果如图4所示，图中ugs为开关管驱动电压。

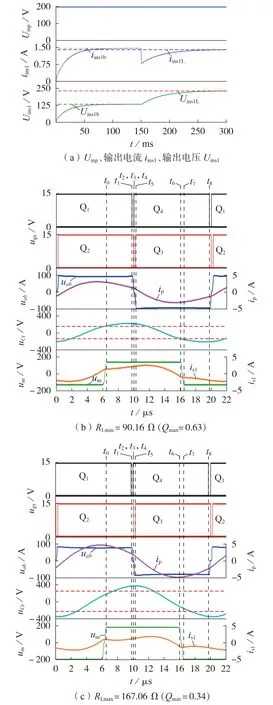
图4 一倍准恒流模式仿真波形Fig.4 Simulative waveforms for one-time QCC mode

图4（a）显示：在仿真前段RLmin=90.16 Ω下，输出电流iins1b≈1.467 A，输出电压Uins1b≈132.3 V，输出功率P1b≈194 W；在仿真后段RLmax=167.06 Ω下，输出电流iins1L≈1.400 A，输出电压Uins1L≈233.9 V，输出功率P1L≈327.5 W。计 算 得 到H1max=iins1b（/2iinp）≈0.416 8，H1min=iins1L（/2iinp）≈0.397 8，M1max=Uins1L/Uinp≈1.169 5，M1min=Uins1b/Uinp≈0.661 5。以此校验准恒流，可得H1max-H1min≈1.9 %，M1max/M1min≈176.8 %，|(H1max-4/π2)/(4/π2)|≈2.83 %，|(H1min-4/π2)/(4/π2)| ≈1.85 %。仿真结果证明变换器实现了输出工况筛选算法中给定精度内的准恒流输出特性。

图4（b）经处理形成类似图A1的表示。［t0，t1），uab保持Uinp/2=100 V，um保持Uins1b=132.3 V，ip极性未变，持续给Cr充电，uCr保持上升并大于um（横虚线），导致is1不断上升；［t1，t2），t1时刻关断Q1，在tDTb内，uab由Uinp/2下降至0，这之后Q4在t2时刻导通以实现ZVS，又由于α=tDTb·2πfs，则t2、t3、t4时刻重叠；［t4，t5），t4时刻关断Q2，在tDTL内，uab由0下降至-Uinp/2，这之后Q3在t5时刻导通以实现ZVS；［t5，t6），ip下降过零并导致uCr下降，当uCr=um时is1达到峰值，此后is1逐渐减小并过零；［t6，t7），当uCr＜um时，is1过零导致um由Uins1b逐渐下降至-Uins1b；［t7，t8］，um维持-Uins1b，变换器准备进入下半工作周期。对比可知仿真结果与1.2节理论分析基本相同。图4（c）的暂态分析可参考图4（b），但在不同的输出工况下，根据式（9）、（15）—（17），φ随Q减小而减小并导致ip（Ts/2）变大，则ZVS换流过程变短，因此uab输出更加明显的三电平。

3.3 二倍准恒流模式仿真实验

根据1.3节，由于二倍准恒流模式的输出uab也为三电平Uinp/2、0和-Uinp/2。因此，除变换器输入端口电压改为Uinp/2外，电流、电压指标将与图4（a）基本相同。但二倍准恒流模式uds=Uinp/4是一倍准恒流模式uds=Uinp/2的一半，而ip（即ip（Ts/2））相似，则根据式（16）、（17），二倍准恒流模式ZVS换流过程所需tDTb将是一倍准恒流模式的一半。为显示对比效果，维持一倍准恒流模式死区，最终仿真结果如附录A图A5所示。

图A5（a）中同样可计算出H2max=2H1max≈0.833 5，H2min=2H1min≈0.795 5，M2max=2M1max≈2.339，M2min=2M1min≈1.323。以此校验准恒流，可得H2max-H2min≈3.8 %，M2max/M2min≈176.8 %，|(H2max- 8/π2)/(8/π2)|≈2.83 %，|(H2min-8/π2)/(8/π2)|≈1.85 %。仿真结果同样证明，尽管二倍准恒流模式将加剧电流增益波动，但仍实现了给定精度内的准恒流输出特性。而图A5（b）、（c）的暂态分析可参考一倍准恒流模式。但在前段和后段输出工况的［t1，t5），二倍准恒流模式相较于一倍准恒流模式输出uab的三电平更明显。

4 实验验证与分析

4.1 样机参数及实物

样机参数与仿真相同，补充具体器件规格，如附录A表A2所示。所搭建样机实物如附录A图A6所示，采用对称布局，独立设计RTM，驱动控制板尽可能贴近有源桥，降低开关管驱动信号干扰。实验结果中ugs、uds下标中Q1、Q2分别代表开关管Q1、Q2。

4.2 样机实验结果

考虑驱动延迟以及实际器件差异，在仿真基础上，对一倍准恒流模式部分参数进行调整，其中tDTb、tDTL分别取0.3 μs、0.5 μs，α取π/25，RLmin（Qmax= 0.63）、RLmax（Qmin=0.34）分别取90 Ω、163.6 Ω。一倍准恒流模式实验结果如图5所示。

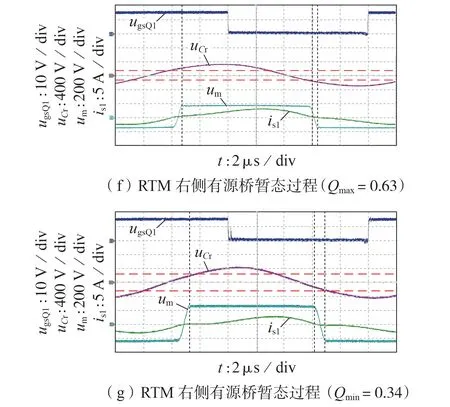
图5 一倍准恒流模式实验波形Fig.5 Experimental waveforms for one-time QCC mode

图5（a）中输入端口电压Uinp=200 V，iins1b≈1.6 A，Uins1b≈144 V，P1b≈230.4 W；iins1L≈1.5 A，Uins1L≈240 V，P1L≈360 W。计算出H1max=iins1b（/2iinp）≈0.454 4，H1min=iins1L（/2iinp）≈0.426，M1max=Uins1L/Uinp≈1.2，M1min=Uins1b/Uinp≈0.72。H1max-H1min≈2.84%，M1max/M1min≈166.7 %，|(H1max-4/π2)/(4/π2)| ≈12 %，|(H1min-4/π2)/(4/π2)|≈5 %。由于受实际器件差异影响，准恒流输出精度相比仿真有所下降，但实验结果与仿真结果基本一致，验证了一倍准恒流模式实现了准恒流输出特性。图5（b）中，不同输出工况下，输出uab均为三电平，即Uinp/2=100 V、0、-Uinp/2=-100 V。且ip相位均滞后于ufund相位，但φ随Q减小而减小并导致ip（Ts/2）变大，因而缩短了ZVS换流过程使三电平更加明显，对比图5（c）中ZVS实现效果，可知样机实验进一步验证了3.2节仿真结果。此外，对比图4（b）、（c）与图5（f）、（g），除波形幅值上的差别外，两者具备相同的暂态过程，验证了1.2节理论分析。

同样维持一倍准恒流模式死区，二倍准恒流模式实验结果如附录A图A7所示。图A7（a）中输入端口电压Uinp/2=100 V，电流、电压指标与图5（a）基本相同。计算出H2max=2H1max≈0.908 8，H2min=2H1min≈0.852，M2max=2M1max≈2.4，M2min=2M1min≈1.44。H1max-H1min≈5.68 %，M2max/M2min≈166.7 %，|(H2max-8/π2)/ |(8/π2)≈12 %，|(H2min- |8/π2)/(8/π2)≈5 %。实验结果与仿真结果也基本一致，验证了二倍准恒流模式也实现了准恒流输出特性。图A7（b）、（c）与图5（b）、（c）基本相同，但各工况下uab三电平更加明显，同时存在电压耦合导致零电平振荡现象。通过对比图A7（d）、（e）与图5（d）、（e）的开关管ZVS实现效果，其中udsQ1、udsQ2均由Uinp/2=100 V降至Uinp/4=50 V，表明样机实验中二倍准恒流模式ZVS换流过程短于一倍准恒流模式，由此可验证3.3节相关仿真结果。对比图A5（b）、（c）与图A7（f）、（g）可知，除了波形幅值上的差别外，两者也具备相同的暂态过程，验证了1.3节理论分析。此外，图A7（h）、（i）证明uab由uao耦合umo形成，同时也叠加了部分TXp电压耦合振荡。而图A7（j）、（k）中ip=iTXp，则证明TXp箝位作用实现各桥臂自均流，意味着LABA开关管ZVS实现情况可直接参考LMBA。

4.3 样机效率分析

作出一倍、二倍准恒流模式在输出工况RLmin=90 Ω（Qmax=0.63）～RLmax=163.6 Ω（Qmin=0.34）范围的准恒流、效率ηp曲线，如图6所示。

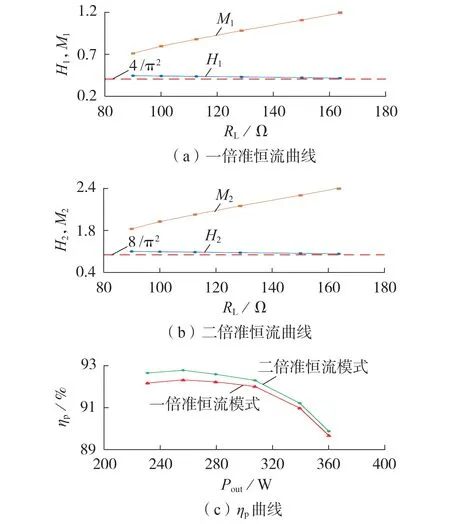
图6 样机准恒流、效率曲线Fig.6 QCC and efficiency curves of prototype

图6（a）、（b）显示，在筛选出的输出工况范围内，随着负载电阻RL增大，2种模式下H1和H2均分别维持在自然恒流增益点（4/π2和8/π2）附近，而M1和M2均持续增大，也表明可实现动态准恒流输出特性。另对比2种模式开关暂态差异，并分析损耗组成，可以发现一倍准恒流模式相较于二倍准恒流模式不存在TXp原边绕组铜损，但由于各开关管具有更高的uds，关断损耗明显增大，而本次样机设计功率较小，运行频率较高，因此关断损耗将会大于绕组铜损，并最终导致图6（c）中二倍准恒流模式的ηp优于一倍准恒流模式。此外，已知Q越小则φ越小，θ越大，也即增大η会减小ηp，将所得参数值fn= 1.1和Qmin=0.34代入式（9）、（12）、（13），求得理论上的ηp最小值ηpmin=90.36 %，而图6（c）显示2种模式在所设计输出工况下ηp最小值均接近ηpmin，由此验证了2.3节中所设计的无功功率限制条件。

5 结论

本文提出一种新型双向倍流LCL-T谐振变换器，在3L-CNPC有源桥中，通过耦合变压器级联各子桥臂交流侧，据此设计不同调制方式控制谐振腔输入电压以建立一倍、二倍准恒流模式，使变换器具备可倍增电流增益的准恒流输出特性。

1）通过分析各模式开关暂态中电流路径，可视一侧有源桥为全桥整流电路，并通过基波分析法建立等效运算电路；

2）为实现双向功率传输特性一致，利用等效运算电路，分析无功功率控制和实现开关管ZVS限制条件；

3）基于各限制条件，设计满足给定准恒流输出精度的输出工况筛选算法，并通过仿真与实验证明了所提新型变换器能够在筛选出的输出工况下，实现给定精度内的准恒流输出及各桥臂自均流。

附录见本刊网络版（http：//www.epae.cn）。