基于Optistruct的云粒子组合探测器改装结构优化设计

鲜章林，武亮

（中国飞行试验研究院试验机设计改装研究部，西安 710089）

0 引言

飞机结冰常常会给飞行安全带来极大的危害，因此在运输机型号试飞科目中，自然结冰试飞是型号合格审定过程中必须面对的风险科目之一。云粒子组合探测器（CCP）[1]作为主要的结冰气象探测设备，是试验机改装中的一个常规项目。在运输机改装过程中，根据机体结构的改装难易程度，云粒子组合探测器一般加装在机身背部区域。为最大程度减少机身迎角和机身表面气流对探测器的影响，同时最大程度保证气象测量的精确性，运输机上一般要求云粒子组合探测器凸出飞机表面700～800 mm之间，因此需要对应高度的改装结构对云粒子组合探测器进行加装。

为保证飞行试验的安全性，且没有计算机仿真软件进行数值计算作为理论支撑，传统的云粒子组合探测器改装结构的设计较为保守，结构质量偏重。此外，传统的云粒子组合探测器改装结构设计因人而异，改装形式较多，与改装当前倡导的标准化和模块化改装理念相违背，同时不利于改装技术的继承和发展。

针对上述问题，本文以某试验机云粒子组合探测器改装结构为研究对象，基于OptiStruct进行结构的拓扑-尺寸联合优化[2]设计，获得可保证结构关键位置变形约束、满足最大静力约束、保持一阶固有频率、保证结构稳定性的轻量化结构。同时，基于上述优化设计，促进云粒子组合探测器改装结构的标准化，从而为后续试验机类似改装结构设计提供参考。

1 优化方法

1.1 拓扑优化

通常情况下，拓扑优化[3]主要针对最初的概念设计阶段，其主要目的是使结构在指定的设计区域内寻求材料的最佳分布或者最佳结构布局形式，以达到最优的刚度分配，或者是寻找结构最优的载荷传力路径，从而提高结构的特定性能或者减小结构质量[4]。

在OptiStruct模块中，拓扑优化采用变密度法[5]，即以每个单元的密度直接作为设计变量，在0～1之间连续变化，0和1分别代表空或实，中间值代表假想的单元密度值。变密度法中，以单元密度及其弹性模量之间的联系为突破口，以单元密度为设计变量，通过该单元密度来进行拓扑优化，通常以结构质量最小为目标函数。

多工况下，以结构质量最小为目标函数的变密度法的典型拓扑优化模型[5-6]为：

式中：ρi为拓扑优化结构中第i个单元的相对密度；n为设计域内单元总数；K为单元刚度矩阵；U为节点位移向量；F为节点力向量；Sj，k为第k个工况中第j个节点处的位移响应；σmax，k为第k个工况中结构的最大的应力响应；W为结构整体质量。

此时优化问题转换为以ρi为优化变量的数学规划问题，通过相应的寻优算法即可完成该问题的求解，然后通过过滤掉低单胞体积的有限元即可得到优化后的材料分布。

1.2 尺寸优化

目前利用拓扑优化获得结果往往难以直接应用到零件加工中，通常需要参考其材料分布及传力路径并结合加工、装配等其他多方面因素对各个子零件进行重新设计，在获得所有零件形式后利用尺寸优化[6]可以对各子零件的厚度、宽度等特征尺寸进行进一步优化，从而获得最终的零件尺寸。

在目前的大型结构尺寸优化中，由于零件数量众多及有限元单元模型的精细化而导致的优化变量和结构响应规模庞大，工程中往往基于敏度分析技术对实际的优化模型进行简化，将隐式的有限元优化模型简化为显示模型，基于该方法的优化流程如图1所示。

图1 优化流程图

1.3 拓扑-尺寸联合优化

本文通过Catia进行三维建模并借助Optistruct优化分析模块，基于变密度法和灵敏度分析技术，对云粒子组合探测器改装结构进行联合优化，通过三级建模实现改装结构从无到有的结构实现，并对最终结构进行结构有限元验证，主要步骤如下：

第一级：根据云粒子探测器安装高度要求及改装结构气动要求建立改装结构的总体气动外形，根据气动外形建立实体设计域结构有限元模型，材料属性各向同性，以探测器最前端位移为约束，以最小质量为目标函数进行拓扑优化，以获得最优结构布置。

第二级：根据拓扑优化确定结构的总体布局形式后，利用Catia进行二次三维建模，并以此建立有限元模型，对各个零件关键尺寸进行尺寸优化。

第三级：根据尺寸优化结果对有限元模型进行尺寸更新，验证结果，并获得最终的三维Catia结构数模。

2 云粒子组合探测器改装结构优化

某运输机云粒子组合探测器位于前机身背部FR30-FR31框、左1～左2长桁之间，距离机身表面高度约为734 mm。云粒子组合探测器和改装结构的总体气动外形如图2所示。

图2 某云粒子组合探测器改装总体气动外形

根据试验机飞行包线，本文选择飞行高度H=0 km、马赫数Ma=0.6、迎角α=2°和侧滑角β=20°条件下的气动载荷作为计算的极限工况，不考虑惯性载荷。

2.1 拓扑优化

对上述结构建立有限元模型，并对顶部云粒子组合探测器外形进行简化，如图3所示。考虑到改装结构底部与机身连接以及顶部与云粒子组合探测器连接的唯一性，此次拓扑优化只对改装结构的中间区域进行优化，该区域被称为设计域。在拓扑优化有限元模型中，设计域由27 650个体单元组成，安装底座及顶部云粒子组合探测器由6403个壳单元组成。

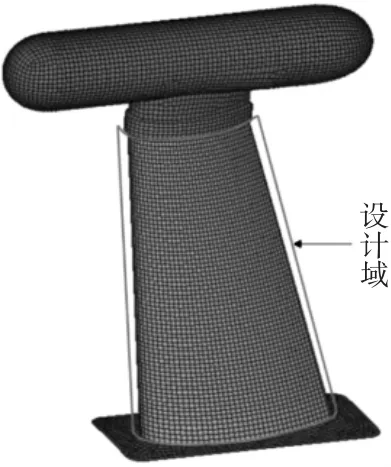
图3 拓扑优化有限元模型

在改装结构底部与机身连接处施加固支约束，利用Inverse-Distance插值算法将CFD气动压力插值到结构有限元模型外表面节点上，以最小质量为目标函数，以探测器前端（节点号：13 242）最大位移及结构最大应力为约束函数，采用变密度法对设计域进行拓扑优化，优化模型表示为：

式中：MASS设计域为设计域零件质量；σmax为所有零件最大VonMises应力；DIS13242为探测器最前端节点位移。

变密度法可以获得设计域内各个单元的密度分布，单元密度的大小体现了该单元对载荷传递的重要性，数值取值为0～1，数值越大则表明该单元对载荷传递的重要性越大，由此即可得到载荷在设计域内的传递路径，图4～图5给出了改装结构的密度分布情况。根据密度分布图可以发现，云粒子组合探测器改装结构在此载荷工况下传力路径特点为：1）前后缘传递载荷较小，主要载荷通过中部高度较高位置由上而下传递至底座；2）随着弯矩由上而下增大，传力路径由上而下逐步加宽；3）左侧出现2条传力路径，且在根部区域汇合；4）右侧顶部区域出现2条传力路径，到中部逐渐汇合，直到根部。考虑到此工况为飞机沿航向向左侧滑20°的情况下产生的，导致左右两侧传力路径不完全对称。

图4 拓扑优化单元密度示意图（0≤单元密度≤1）

图5 拓扑优化单元密度示意图（0.25≤单元密度≤1）

2.2 基于拓扑优化的模型设计

拓扑优化得到的结果在不考虑3D打印等加工方法时往往难以直接进行数控加工，这是由于数控加工工艺约束难以完全应用到拓扑优化中，通常需要依据拓扑优化结果按照工艺及装配需求重新设计结构零件。根据拓扑优化结果，同时考虑到实际飞行中左右侧滑的可能性，在图5的基础上，保证气动外形不变的情况下，对改装结构进行优化设计。优化后的模型主体采用典型的“薄蒙皮梁式”翼面结构，由翼梁、翼肋和蒙皮等组成，三维模型如图6所示，主要零件包括探测器连接接头、端肋、中间肋（前缘、盒段和后缘）、根肋、前梁、后梁及蒙皮。

2.3 尺寸优化

依据拓扑优化结果建立的云粒子探测器改装结构反映了整个结构的载荷传递路线，但各个零件的具体尺寸均根据以往经验进行设置，缺乏详细数值分析依据，为验证零件尺寸的合理性并发掘各个零件的减重潜力，基于敏度分析及尺寸优化算法对改进后的改装结构各零件尺寸进行优化。依据图6所示的改装结构重新创建有限元模型（如图7），采用壳单元对所有零件进行建模，单元数量为17 981，单元厚度取实际零件厚度。

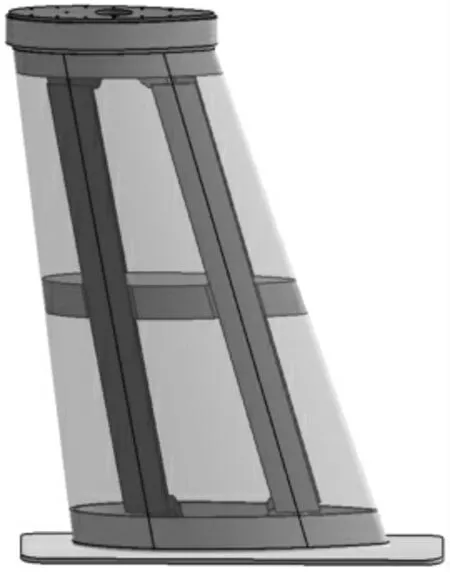
图6 基于拓扑优化的改装结构三维模型

图7 进行尺寸优化的改装结构有限元模型

按照本文选择的极限工况对云粒子组合探测器改装结构进行静强度分析，得到结构变形云图和应力云图，如图8所示。根据初步有限元分析，初始结构设计较为保守，能够满足极限工况中强度和刚度要求，最大VonMises应力为71.38 MPa，云粒子组合探测器最前端的最大变形为2.174 mm。结构存在优化空间，为此在保留各零件拓扑形式的前提下对零件各特征厚度进行优化。

（a）变形云图 （b）应力云图

根据各零部件结构形式，以各零件特征厚度为优化变量，设计变量共17项，设计变量取间隔为0.1 mm的离散值，设计变量信息如表1所示。为保证静强度要求，约束结构最大应力小于270 MPa；为保证关键位置变形要求，约束云粒子组合探测器最前端不大于2.0 mm。整个优化的目标函数选择为最小结构质量，由此得到优化模型为：

式中：ti为第i个设计变量厚度；timin、timax为第i个设计变量取值上下限；DIS13242为探测器最前端节点位移；MASS改装零件为所有改装件质量。

经过迭代优化后，得到设计变量优化终值如表1所示，根据优化后的厚度分布对优化前后改装结构的一阶固有频率、一阶屈曲特征值进行了对比计算，优化前后各响应的变化如表2所示。优化后一阶固有频率基本保持不变，一阶屈曲特征值减小到5.23＞1.5，各响应值满足约束及安全系数要求，优化前后改装结构的质量分别为13.21 kg和10.26 kg，质量降低了2.95 kg，为初始结构质量的22.33%，优化效果良好。

表1 设计变量信息

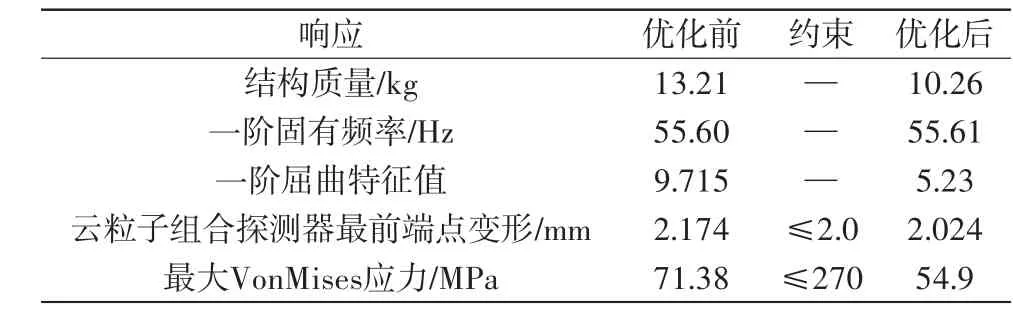
表2 改装结构响应变化信息

3 结论

本文以某运输机云粒子组合探测器改装结构为研究对象，在总体气动外形确定的情况下，通过Optistruct软件利用拓扑优化确定结构的最优布局形式，并完成了改装结构的布局设计，在此基础上，以改装结构质量最小为目标函数，以探测器前端最大变形为约束，对各零件的特征厚度进行了尺寸优化，获得了满足预定刚度、强度约束的较小质量改装结构，优化结果显示质量减小了22.33%，减重效果明显。

通过上述研究证明了拓扑-尺寸联合优化设计在试验机改装结构设计中的显著作用，即优化结构布局形式、减轻结构质量、提高设备装载能力。因此，在结构设计的不同阶段应用不同的优化方法能为设计者提供清晰的设计思路，多种优化方法的联合使用可以更有效地满足设计需求。