双有源桥DC-DC变换器线性自抗扰控制

李 山,姚桂杨,杨 奕,向文凯,马 雯,王 钦

(1.重庆理工大学 电气与电子工程学院， 重庆 400054； 2.重庆市能源互联网工程技术研究中心， 重庆 400054)

0 引言

自“双碳”目标提出以来，可再生能源及电动汽车等领域快速发展并大量接入电网。但其不稳定性与不确定性使传统交流配电网面临巨大挑战[1]。由于直流输电不存在频率、相位问题，传输效率高，控制简单，将成为未来电力系统的重要组成部分[2]。电力电子变压器(power electronic transformer，PET)作为直流输电网的核心枢纽，可作为多电压等级接口，便于可再生能源及储能设备接入。双有源桥(dual active bridge，DAB)DC-DC变换器具有高功率密度、能量双向传输、电气隔离、易于实现软开关等优点，已逐渐成为PET的主流设备[3-5]。

DAB变换器通常采用移相控制，传统单重移相(single phase shift，SPS)通过控制两侧全桥输出方波之间的相位差实现能量的双向传输，但变换器电压传输比不匹配时存在较大的电流应力，会降低DAB变换器效率甚至损坏MOS管。为了减小变换器的电流应力，扩展移相(exteng phase shift，EPS)、双重移相(dual phase shift，DPS)、三重移相(triple phase shift，TPS)控制相继被提出[6]。张勋等[7]采用EPS控制优化电流应力，相比于SPS控制，EPS控制具有更低的电流应力，但其只分析了一种工作模式，控制效果难以达到最佳。曾进辉等[8]基于双重移相控制提出一种分段优化策略，保证变换器全局范围内电流应力最优，但两侧全桥内移相比相同限制了控制灵活性。邓和睿等[9]基于TPS控制提出全功率下的电流应力优化策略，具有最高的控制自由度，在保证软开关的同时将电感电流应力降到最小，但其控制实现较为复杂。

当前DAB变换器的研究主要集中在快速动态响应、电流应力和回流功率优化方面[10]。现有DAB变换器优化控制策略中，大多是对单一目标进行优化。为了同时优化DAB变换器动态性能和电流应力，安峰等[11]基于EPS引入虚拟电压分量对变换器的传输功率进行在线估算以提高其对于负载突变和输入电压突变时的响应能力。郭华越等[12]基于EPS提出了直接功率控制与最小电流应力相结合的方案，实现对动态和稳态性能的同时优化，但其效率参数导致了控制灵活度降低。杨向真等[13]基于EPS提出了一种将电流应力优化方法与电压动态矩阵控制(dynamic matrix control，DMC)算法相结合的控制算法，减小了电流应力，提高了变换器在启动阶段、负载突变、输入电压突变时的动态响应特性。安峰等[14]基于DPS建立变换器输出电压的离散模型并引入前馈控制，结合电流应力优化计算，提高了变换器的响应能力。

上述方案不同程度地提高了变换器性能，但均采用PI控制器实现，针对PI控制存在动态响应慢、抗干扰能力差等问题。本文基于EPS提出了一种线性自抗扰控制(linear active disturbance rejecting control,LADRC)结合直接功率控制(direct power control，DPC)的电流应力优化方案，进一步优化变换器的动态响应及电流应力。自抗扰控制(active disturbance rejecting control，ADRC)[15]不依赖对象模型，能够在扰动明显影响系统输出前主动提取扰动信息，尽快消除扰动，其缺点是控制结构较为复杂。针对ADRC存在的不足，Gao[16]将其改进为线性自抗扰控制，所有控制器和扩张状态观测器都以线性形式实现，控制参数降为3个。尹忠东等[17]将自抗扰控制技术引入电动汽车整流器控制，能够快速、准确地跟踪指令，降低输出电压纹波，提高系统的动态特性，具有较好的抗负载扰动能力。刘科君等[18]基于三相交错并联双向直流变换器提出了一种电压外环线性自抗扰控制，有效抑制了直流母线电压波动，提升了储能系统的动态响应速度和抗干扰能力。

本文中首先分析了DAB变换器在扩展移相控制下各个模态下的输出功率和电流应力特性，建立数学模型；根据KKT(karush-kuhn-tucker)条件求出电流应力最优解；为了提高变换器动态性能，采用线性自抗扰控制器结合直接功率控制方案，在快速改变传输功率、提高变换器动态响应的同时对电流应力进行优化；最后，在Matlab/Simulink和搭建的小功率实验样机上对所提方案进行验证。

1 扩展移相的工作原理

双有源桥DC-DC变换器电路拓扑结构如图1所示。U1、U2分别为输入、输出电压；L、iL分别为辅助电感、电感电流；C1、C2为支撑电容；1∶n为高频变压器匝比，n>1。以能量从U1侧传输到U2侧为例，分析扩展移相的工作原理。

图1 双有源桥DC-DC变换器电路拓扑结构

图2为DAB变换器在EPS调制下的工作波形，分别为0≤D1≤D2≤1、0≤D2≤D1≤1两种运行模式。图中Ths为半开关周期；D1为原边H桥内移相比，0≤D1≤1；D2为副边H桥相对于原边H桥的外移相比，0≤D2≤1；Uab、Ucd分别为两侧H桥输出电压。

由图2可知电感电流具有对称性，即iL(t)=-iL(t+Ths)，可得0≤D1≤D2≤1时半周期内各开关管动作时电流为:

图2 扩展移相控制下的工作波形

(1)

式中：K为电压传输比，K=U1/(nU2)；f为开关频率。

变换器平均传输功率和电流应力分别为:

(2)

(3)

将式(1)代入式(2)，并由式(3)传输功率和电流应力基准值求得相应的标幺值。同理可得0≤D2≤D1≤1时的传输功率和电流应力标幺值，见表1和表2。

表1 EPS控制下DAB变换器标幺化传输功率

表2 EPS控制下DAB变换器标幺化电流应力

2 优化控制方案

2.1 线性自抗扰控制LADRC

传统双有源桥变换器电压环通常采用PI控制器，其控制结构简单，易于实现，但对于复杂系统，PI控制器无法满足系统运行指标，故引入一种响应速度快、控制精度高、鲁棒性强线的性自抗扰控制技术[19]。

线性自抗扰由线性扩张状态观测器(LESO)，线性误差反馈控制率(LSEF)以及扰动补偿因子b0组成，二阶LADRC的基本结构如图3所示。

图3 LADRC基本结构框图

被控对象表示为：

(4)

(5)

对应的线性扩张状态观测器为：

(6)

将特征方程的极点设置到观测器带宽ω0的负数值上，LESO的带宽成为LESO增益矩阵参数的唯一相关量，使得LESO的设计变得更为容易，此时LESO的增益矩阵L可改写为：

(7)

LESF采用比例微分控制器(PD)实现[21]，其形式为：

u0=kp(r-z1)-kdz2

(8)

式中：r为给定值；kp、kd分别为比例系数、微分系数；z1和z2为扩张观测器状态。

进行参数化处理：

(9)

式中：ωc为控制器带宽，成为LESF增益矩阵唯一参数，简化了控制器设计。

2.2 电流应力优化

DAB变换器工作在某一传输功率时，其移相比D1、D2存在多种组合，在满足传输功率时可以选取适当的D1、D2降低电流应力。电流应力优化问题可转换为最优值求解问题。拉格朗日乘子法与KKT(karush kuhn tucker)条件是一种在等式和不等式约束下的最优解求取方法。选取该方法求解最小电流应力，此种方法具有以下标准形式：

(10)

式中：f(x) 为优化目标函数；x为变量；hi(x) 为等式约束条件；gi(x) 为不等式约束条件。

令电流应力标幺值ip为优化目标函数，内外移相比D1、D2为自变量，传输功率p为等式约束条件，移相比D1、D2的取值范围作为不等式约束条件，构造0 ≤D1≤D2≤ 1时KKT条件下的拉格朗日方程为：

(11)

式中：F为拉格朗日多项式；λ为等式约束乘子；μj为不等式约束乘子。

求解可得最优解和最小电流应力表达式为：

(12)

同理,可得0≤D1≤D2≤1时最优解和最小电流应力的表达式为：

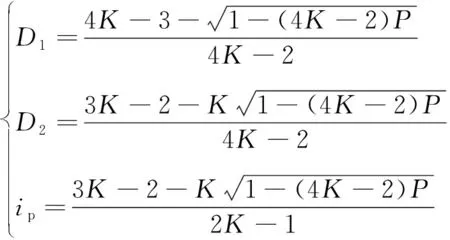
(13)

由上述分析可知，优化控制方案恰好包括了0≤p≤1的整个功率传输范围。

表3给出了关于DAB变换器单重移相与扩展移相控制的最优电流应力值。图4为2种控制方式的电流应力三维图，可以看出，在全功率范围内，扩展移相具有更低的电流应力。

表3 SPS、EPS方案下的电流应力最优解

图4 SPS、EPS电流应力三维图

2.3 直接功率控制方案

为了在优化电流应力的同时进一步提高系统响应速度，直接功率控制方案被广泛采用。本文采用线性自抗扰控制结合直接功率控制方案进行电流应力优化。

直接功率法通过引入电容电流对变换器进行控制，图5为变换器输出侧拓扑图，i为输出侧电流，ic为电容电流，io为输出电流。直接功率控制考虑了支撑电容充放电电流，输出侧功率可以表达为

图5 变换器输出侧拓扑图

Po=U2(ic+io)

(14)

考虑电路中存在的传输损耗，此时传输功率与输出功率的关系式为

(15)

式中：η为传输效率，取决于电路自身特性。

将式(15)标幺化可得：

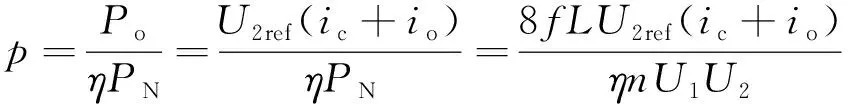
(16)

式中：U2ref为参考电压。

式(16)结合了传输功率与输出功率，当电路状态突变时，立刻改变传输功率。

图6为系统闭环控制框图，由输入、输出电压采样值得到电压传输比K，参考电压U2ref与输出电压U2采样值作差后，由线性自抗扰控制器得到电容电流ic；与输出电流采样值io求和得到输出侧电流i。根据式(16)，得到输出功率标幺值p，将p和电压传输比K代入电流应力计算式(12)(13)，计算得到最优移相比D1、D2，产生对应的驱动信号驱动开关管。

图6 系统闭环控制框图

3 仿真及实验结果分析

为验证所提策略，在Matlab/Simulink建立仿真模型，并搭建基于DSP28335的小功率实验样机进行验证，主要电路参数见表4。

表4 主要电路参数

DAB实验样机实物见图7，由主拓扑、主控芯片、采样电路、驱动电路、可编程电源、电阻负载构成。主要电路参数与表4相同。

图7 双有源桥DC-DC变换器实验样机实物图

为了验证本文所提策略的有效性和优越性，在动态特性实验中将传统PI控制与LADRC控制进行对比实验；在电流应力实验中将SPS控制与EPS优化控制进行对比实验。

3.1 动态特性优化

3.1.1仿真验证

当输入电压Uin=30 V，输出电压Uo=50 V时，图8给出了采用PI控制器和LADRC控制器的启动波形。采用PI控制时超调量为约为3%，调节时间约为2.5 ms，采用线性自抗扰控制基本无超调，调节时间约为0.6 ms。

图8 PI、LADRC启动波形

图9和图10给出了传统PI控制与线性自抗扰控制下，负载由40 Ω切换到20 Ω、再由20 Ω切换到40 Ω时的输出电压电流仿真波形。负载切换时采用PI控制输出电压动态响应较慢，调节时间约为5 ms，电压波动为0.5 V，而线性自抗扰控制的响应速度为 2 ms，电压波动为0.1 V，电压响应速度提高了60%，电压波动降低了80%。

图10 LADRC动态响应波形

3.1.2实验验证

图11和图12为PI控制与LADRC控制下的动态响应实验波形。可知，在PI控制下，负载突减、突增时系统的电压波动约为2.3 V，动态响应时间约为60 ms；在LADRC控制下，负载突减、突增时系统的电压波动约为1 V，动态响应时间约为25 ms；变换器动态响应速度提高了约58%，电压波动值降低了约56%，表明所提控制策略能够快速、准确地跟踪参考值，输出电压基本保持稳定，并具有较高的动态响应速度。

图11 负载突减动态响应实验波形

图12 负载突增动态响应实验波形

3.2 电流应力优化

3.2.1仿真验证

图13和图14为输入电压30 V、输出电压50 V，负载分别为40、20 Ω，SPS控制和EPS控制下系统稳定工作时的一次侧电压Uab、二次侧电压Ucd、辅助电感电流iL的仿真波形。

图13 R=40 Ω时的电压电流波形

图14 R=20 Ω时的电压电流波形

负载为40 Ω时，SPS控制下的电流应力为6.13 A，EPS控制下的电流应力为5.58 A，电流应力值降低了约9%；负载为20 Ω时，SPS控制下的电流应力为7.92 A，EPS控制下的电流应力为7.48 A，电流应力值降低了约5.6%。由仿真结果可以看出，EPS控制有效降低了电流应力，提高了变换器稳态性能，具有更好的控制效果。

3.2.2实验验证

图15和图16给出了输入电压为30 V、输出电压为50 V，负载分别为40、20 Ω，传统SPS控制和EPS控制达到稳定时的变压器一次侧电压Uab、二次侧电压Ucd、辅助电感电流iL实验波形。

图15 R=40 Ω时的电压电流波形

图16 R=20 Ω时的电压电流波形

在SPS控制下，40 Ω时电流应力为6.6 A，20 Ω时电流应力为8.4 A；在EPS控制下，40 Ω时电流应力为5.8 A，20 Ω时电流应力为7.8 A，电流应力值分别降低了12%，7.1%。EPS优化控制下变换器电流应力明显下降，能够降低系统损耗，提高变换器稳态性能。

4 结论

1) 线性自抗扰控制相比PI控制，负载突变时电压响应速度提高了约58%。可实现几乎无超调启动，具有较强的可移植性及适用性，可推广到回流功率优化等领域。

2) 相比单重移相控制，扩展移相控制自由度更高，电流应力优化能力更强，实验中负载为40 Ω和20 Ω时，电流应力分别降低约12%和7.1%，所采用的电流应力优化控制策略有效降低了电流应力，提高了变换器的稳态性能。