改进模糊神经网络的校直行程预测
陈明灯,郝建军,杨治刚,叶志雄,梁 建
(重庆理工大学 机械工程学院, 重庆 400054)
0 引言
在车辆、机械、纺织、军工等行业,轴类零件被大量使用。在生产加工过程中,轴类零件处理不当会发生弯曲,此时需要对零件进行校直处理。传统的校直方法是操作工人凭经验控制校直压头的行程,校直速度慢且校直精度低。近年来,计算机技术迅速发展,机器学习在预测模型领域取得了显著成绩。在轴类零件校直系统中,石钧仁[1]采用BP神经网络模型对校直机工件下压量进行预测,并利用支持向量机对校直机工件弯曲量测量误差进行预测和补偿。Jafarzadeh[2]运用模糊神经网络模型,采用均匀混合学习算法预测风电场发电量,提高了风电预测精度和效率。郝建军等[3]在校直行程预测中运用PSO-LSSVM算法对模型进行优化,解决了寻优缺陷问题,预测精度高。Pramoda[4]根据模糊规则选择合适的框架,提出了基于相似性的数据预测,并使用混合蚁群粒子算法优化网络,提高了预测精度。宋明达等[5]针对电力系统负荷数据建立Elman神经网络预测模型,提高了预测的准确性与可行性。Lu等[6]采用理论分析和实验建立了校直行程预测模型,并通过有限元分析进行比较,提高了预测精度。
当前,利用模糊神经网络对校直机校直行程预测的研究还不够深入。本文在模糊神经网络基础上对其网络结构进行优化,提出一种改进型模糊神经网络预测模型来预测校直行程,将神经网络和模糊系统的优势应用到模型中,使预测精度进一步提高。
1 基本理论
1.1 校直行程计算
目前,国内学者一直致力于研究如何精确计算校直机校直行程。李骏等[7-8]对理论计算方法进行了总结和归纳,包含基于弹塑性力学的理论计算方法、基于有限元的方法、基于经验公式的计算方法等。针对轴类零件一般采用三点式反弯校直法[9]进行校直,将零件两端固定在2个支撑物上,在零件中点上方施加压力进行校直。其计算原理可近似为一简支梁在受力作用下产生变形情况,两端简支梁,中点加压,其校直过程如图1所示。

图1 校直过程示意图
图1中,AB为弹性变形阶段,BC为弹塑性变形阶段,CD段为弹性恢复阶段。假设AB与CD近似平行,B点为零件屈服点,在集中压力F作用下发生变形。在弹塑性阶段,材料受力发生弯曲变形,轴类零件在弯曲后会恢复一部分变形量,没有恢复的部分残留下来,其压力校直原理[10]如图2所示。
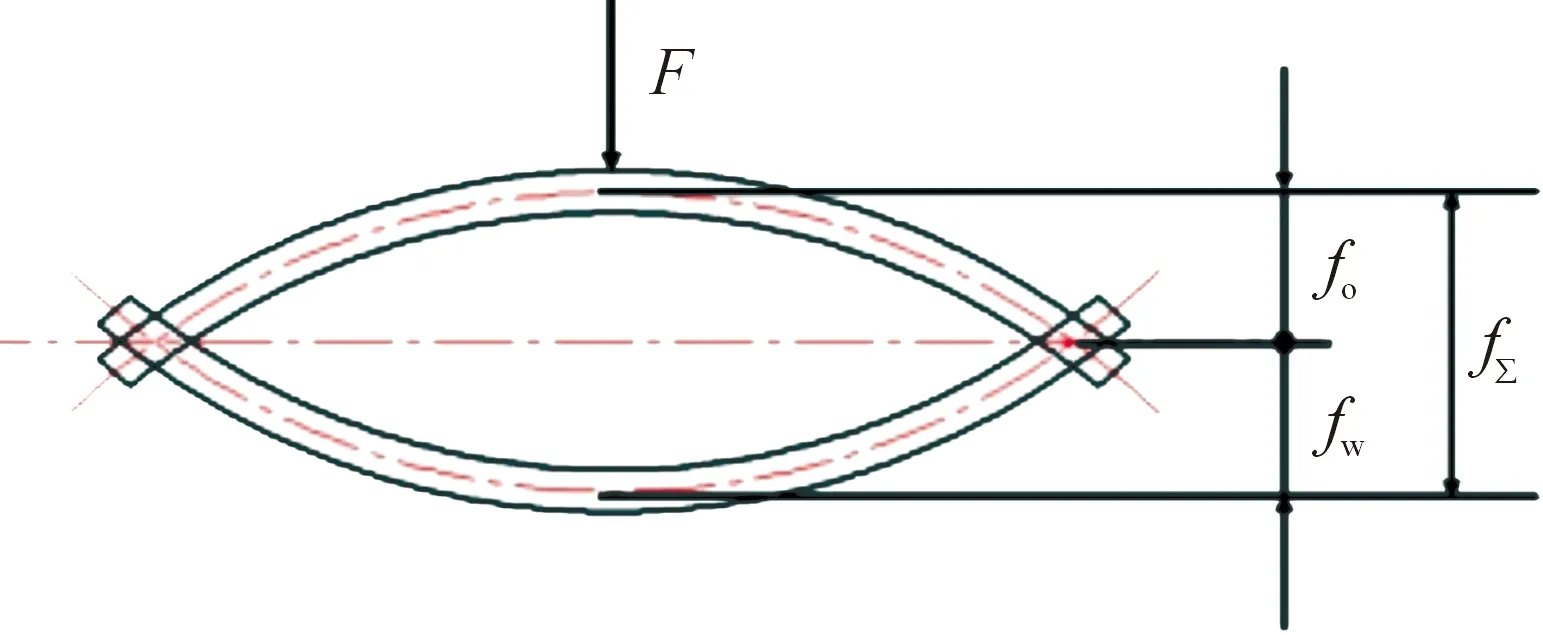
图2 压力校直原理图
若卸载压力后回弹量与反弯量数值大小相等,则该零件校直成功,校直行程可表示为:
fΣ=fo+fw
(1)
其中:f0为初始变形量;fw为反弯变形量;fΣ为校直行程。
1.2 模糊神经网络
模糊神经网络主要包含神经网络和模糊系统两板块,其结构类似于神经网络,对信息能够逐层进行分析;功能上则是模糊系统[11],可以将模糊规则运用到信息中。模糊神经网络中各个结点、参数等都按照模糊系统模型建立,输入输出关系能够很快收敛,参数学习和调整较容易,且具有自学习能力,能够准确地完成校直机校直行程预测关键问题。
1.3 模糊推理系统
将模糊推理系统运用在校直行程预测中。基于逻辑关系及推理规则,融入成功校直的经验、方法,将校直行程预测参考指标进行并行分布处理,同时对工件形状、支撑间距、变形角度等进行考虑。与传统校直行程预测模型相比,能提高计算容错性和鲁棒性,同时具有较强的自学习能力,可广泛运用于多变量系统中。
1.4 网络结构
模糊神经网络结构种类多,分布复杂,本文中选择具有5层结构的模糊神经网络[12]进行分析,其结构如图 3所示。网络主要分前件网络和后件网络两部分,前件网络为前4层,用来表示模糊规则前件,后件网络为第5层输出,用来产生模糊规则后件。

图3 模糊神经网络结构示意图
网络迭代算法为误差反向传播法,通过对每个神经元的输入和输出关系进行分析,得到该网络迭代算法计算步骤。如图 4所示,神经元模型[13]为模糊神经网络结构中第p层第q个节点。

图4 神经元模型
输入为:
(2)
输出为:
(3)
对于一般的神经元节点,通常有
(4)
(5)
由单个神经元输入输出关系求解得到该5层网络结构的每一层节点函数。
第1层:
(6)
其中:i=1,2,…。
第2层:
(7)
其中:i=1,2,…;j=1,2…。
第3层:
(8)
第4层:
(9)
其中:j=1,2,…,m。
第5层:
(10)
其中:i=1,2,…,r。
设误差代价函数为
(11)
式中:ydi和yi分别表示期望输出和实际输出。需要学习的参数主要是连接权wij、隶属度函数的中心值cij和宽度σij。

(12)
从而得到所求1阶梯度为:
(13)
最后,得到参数调整的学习算法如下:
(14)
(15)
(16)
其中:η为学习率,η>0。
2 改进模糊神经网络
在轴类零件校直过程中,校直一次就成功的概率较低,往往需要进行多次校直才能达到要求。在多次下压的过程中,后一次下压量数值基于前一次下压量数值。基于此,提出一种改进型模糊神经网络结构。该结构主要创新点是在网络前件中设计承接层,当输入样本经过隐含层后,不直接进入模糊规则选项,而是从隐含层进入承接层。承接层可以将隐含层前一时刻输出值记忆下来,即对前一次下压量数据进行保存,经过存储之后再输出到隐含层。这种动态递归的网络模型能够对历史数据进行操作,对下压量进行修正,从而得到更精确的校直行程预测值。
2.1 网络结构
采用模糊系统与Elman神经网络相结合[14],将网络结构设置为6层。改进的模糊神经网络结构见图5[12]。

图5 改进的模糊神经网络结构示意图
第1层为输入层,将参考指标数据作为输入,输入值x=[h1,h2,…,hn]Τ,该层节点数为M1=n。
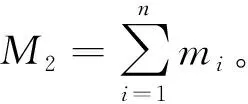
(17)
其中:xi表示隶属度值;i=1,2,…,n;j=1,2,…,mi;是输入向量的维度数;mi是xi的模糊子集数;cij表示隶属度函数的中心;σij表示隶属度函数的宽度。
第3层是承接层,将隐含层前一时刻得到的隶属度值保存在该层,对数据进行存储,并将当前时刻数据输出。
第4层为模糊化层,节点表示模糊规则,每条规则与隶属度之间都有一个匹配度,通过式(18)来计算其适用程度[15],即
(18)
该层节点总数为M3=m。
第5层节点数与第4层相同,即M4=M3=m。用作归一化计算,按照式(19)将数据映射到要求范围中,有利于网络进行数据学习与计算。
(19)
第6层是输出层,将第5层归一化后的数据进行解模糊化,也就是清晰化计算。整个网络输入、输出关系[16]如下:
(20)
其中:wj为承接层至隐含层的连接权值;wi为输入层到隐含层的连接权值;wr为隐含层至输出层的连接权值;xc(τ)为承接层输出;τ为当前时刻,τ-1为前一时刻。
2.2 学习算法
网络学习算法[17]中,需要调节的参数有wi、wj、wr、θi(τ+1)、θr(τ+1)。其中,θi(τ+1)为隐含层输出阈值;θr(τ+1)为输出层输出阈值。网络误差函数通过式(21)来表示。
(21)
其中:P为样本总数;ydi和yi分别表示期望输出和实际输出。可以得到
(22)
同理,可得出隐含层到输出层的权值wr(τ+1)和输出层阈值θr(τ+1)的调整方法:
(23)
递推关系式如下:
xc(τ-1)=x(τ-2)
(24)
将式(24)展开下去,就能得到任一时刻的值。xc(τ)动态递推计算过程具有更强的计算能力,能很好地解决参数寻优问题,网络稳定性提高,适应变化能力得到改善,校直行程预测更精确。
2.3 稳定性分析
采用李雅普诺夫(Lyapunov)稳定性理论分析本文网络结构的稳定性[18]。通过分析可知,网络误差函数为
(25)
令ei=ydi-yi,则式(25)变为
(26)
根据Lyapunov定理,网络稳定的充分条件是
ΔE(τ+1)=E(τ+1)-E(τ)<0
(27)
即
(28)
当网络的权值变化较小时,可以将ei(τ+1)进行泰勒展开,得到
(29)
将式(29)代入式(28)整理得:
(30)
在权值变化小的情况下,对Δw进行如下分析:
(31)
将式(31)代入式(30)得到
(32)
整理得
(33)
同时,由式(28)可以得到
(34)
令
(35)
则学习率的范围为
(36)
学习率影响网络的稳定性,应在该范围内选取合适值。
改进的模糊神经网络算法流程见图6。

图6 改进模糊神经网络算法流程框图
3 校直行程仿真实验与结果分析
从轴类零件校直现场获取300个零件的成功校直数据,数据指标包括校前变形角度、校后变形角度、校前变形量、校后变形量、校直次数、最终校直行程等,将校直行程作为单输出,其余指标作为输入。
3.1 模糊神经网络模型仿真结果
以Matlab为运行环境,选用Fuzzy工具箱,为避免实验结果的偶然性,取300个校直成功零件共742组数据进行仿真。随机选取446组数据作为此次实验的训练样本,148组数据作为测试样本,148组数据作为验证样本。
将所有数据相应导入工具箱中。考虑校直影响因素有5个,所以输入样本数设置为5,隶属度函数设置为5;目标误差设置为0.005;迭代次数设置为1 000,得到如图 7所示的模型结构示意图。

图7 模型结构示意图
第3层的各个节点表示一条模糊规则,对于多输入、单输出系统,可以采用IF条件语句,如下所示:
ifx1isA1andx2isA2, thenu=f(x1,x2)
将作为校直机校直行程影响因素的5个参数指标作为输入,一个输出就是实际校直行程。
三角形隶属函数、梯形隶属函数、π函数隶属函数、高斯型隶属函数等函数值是位于[0,1]区间内的函数,但高斯函数的计算具有可分离性,能在高维中实现快速计算。考虑到高斯函数具有旋转对称性,能够平滑地、差别很小地进行计算,所以选取高斯型隶属函数进行分析。模型训练结果如图8所示。
图8(a)中校直成功的446组数据作为训练集,图8(b)中148组数据作为测试集,图8(c)中148组数据作为验证集。在各个数据集中,预测值与实际值分布较均匀,拟合程度高,只有少数几组数据存在较大偏差,在误差允许范围内通过调整参数可以提高数据的准确度。该模糊神经网络预测模型训练集误差为2.09 mm,测试集误差为2.11 mm,验证集误差为2.06 mm,相对误差为3.8%。该模型可用来检验预测结果的准确度。

图8 模型仿真结果
将模糊推理结果用三维图进行展示,如图9所示。
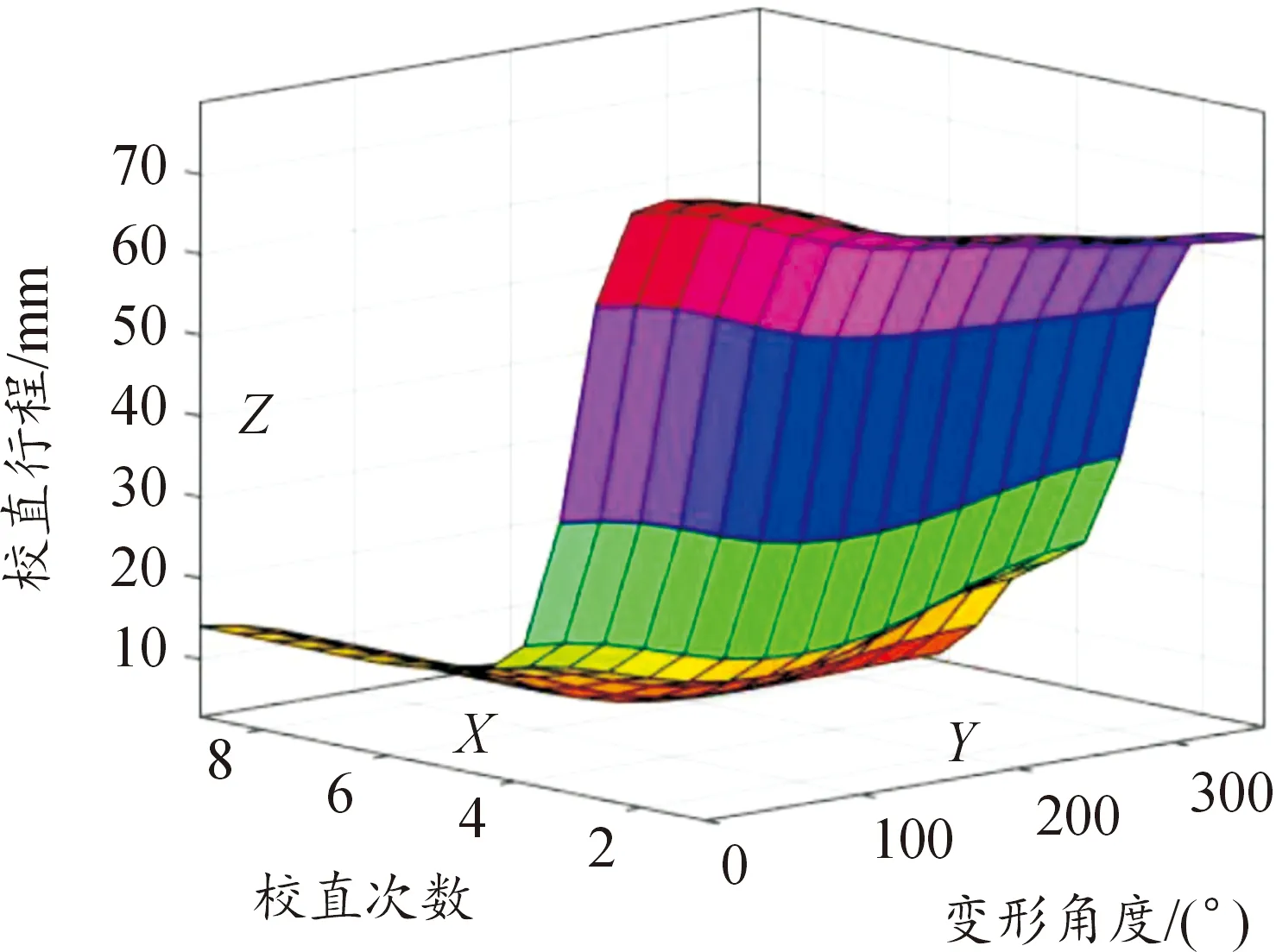
图9 推理结果图
图9中,X轴为校直次数,Y轴为角度变形量,Z轴为校直行程。可以看到,校直成功次数与角度变形量的相关性较大,随着校直次数的增加,其角度变形量会逐渐变化,整体趋势向上,校直行程在一个区间内发生变化,可以通过设置不同的参考指标实时观测校直行程的变化情况。
将148组预测值的数据从系统中导出,与实际148组数据进行对比,拟合成曲线,如图10所示。
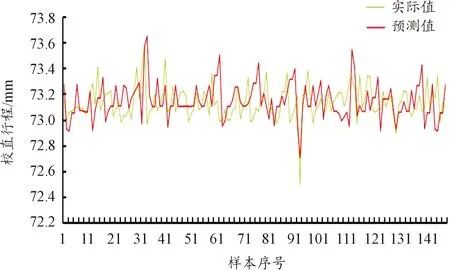
图10 实际值与预测值曲线
在148组验证数据中,整体拟合效果较好,总体平均误差为2.43 mm,但也有个别情况存在较大偏差,单个数据最大误差为2.61 mm,相对误差为4.1%。数据预测偏差较大情况仍然存在,预测精度有待提高。将模型迭代误差曲线导出,如图11所示。

图11 误差迭代图
分析图11发现,随着迭代次数的增加,模型预测误差不断降低,在第165次迭代时,误差达到最低。仿真结果证明了模糊神经网络在校直行程预测过程中的可行性,为改进模糊神经网络及优化提供了思路。
3.2 改进模糊神经网络的仿真结果
利用Matlab软件,选取300个校直成功零件共742组数据进行仿真。按照比例随机选取446组数据作为本次实验的训练样本,测试样本和验证样本分别为随机选取的148组数据样本。样本数据选择与模糊神经网络保持一致。
首先将数据随机按照3∶1∶1划分为训练集、测试集、验证集,有利于网络进行数据学习;然后对数据进行归一化处理,使用mapminmax函数,数据经过处理均映射到[0,1]区间,这样可以消除特征指标量纲和数据误差范围大的影响,同时提高网络收敛性。归一化处理方法如下:
x′=(x-xmin)/(xmax-x)
(37)
其中:xmin为样本最小值;xmax为样本最大值;x为数据归化前的值;x′为数据归化后的值。
网络训练计算较复杂,训练时间长,对样本数据量有一定限制要求。本文中采用进退法[19]来确定隐含层节点个数,相比于经验公式,该方法更准确,能极大缩短计算时间,提高网络运行效率。
采用改进模糊神经网络进行校直行程预测,取50组数据来展示预测值和实际值的情况,得到如图12所示的校直行程预测曲线。

图12 改进模糊神经网络校直行程预测曲线
从图12中可以看到,数据整体拟合程度高,局部出现偏差概率小,峰值误差较之前小,整个数据预测误差范围明显降低。取50组预测数据的相对误差进行整理,所得结果见表1所示。
对于表1中的数据,将误差全部取绝对值,求得改进模糊神经网络预测最大误差为1.05 mm,总体平均误差为0.83 mm。取每个零件的相对误差,求得相对误差的平均值为1.35%。相比模糊神经网络预测方法,新算法误差减小,相对误差提高了2.77%,且网络训练速度更快,优化了网络结构,避免局部峰值偏差大。该网络满足校直行程预测结果,并大大提高了预测精度。2种预测模型的误差情况见表2。
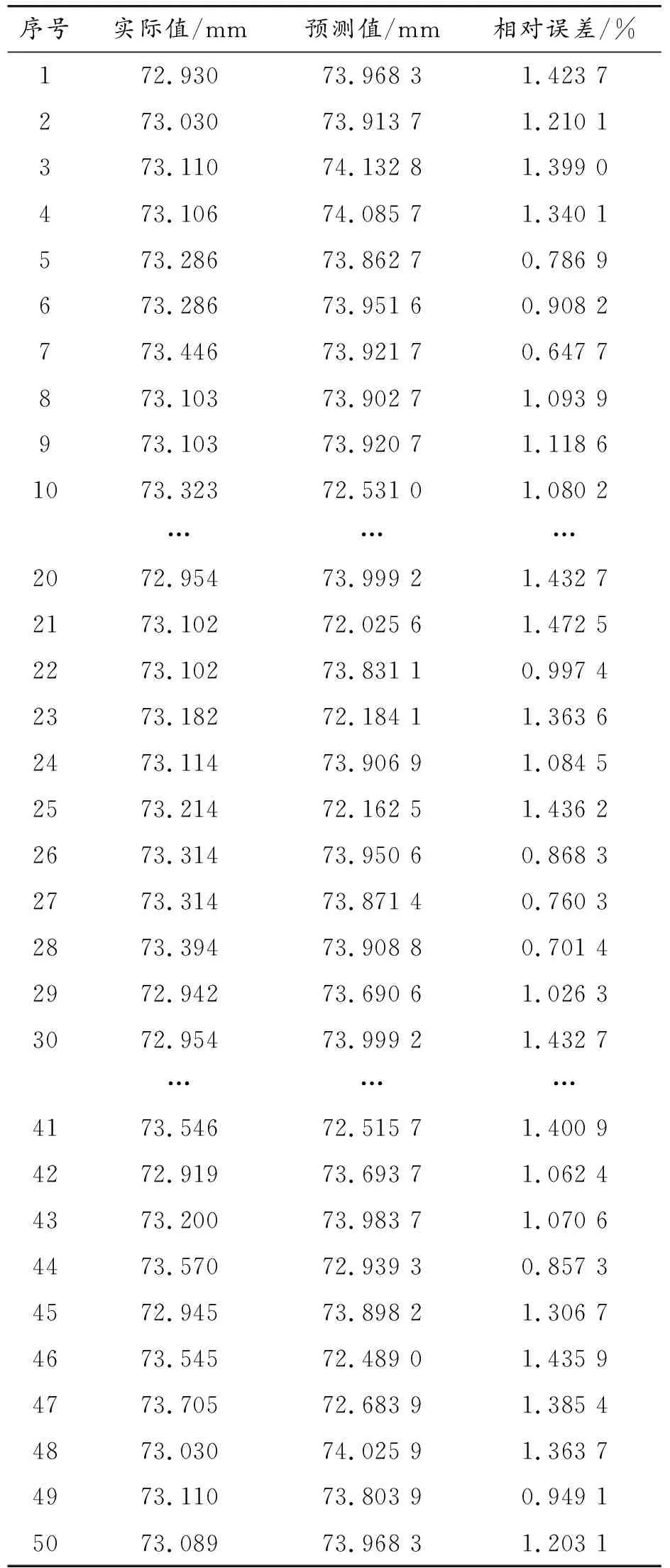
表1 改进模糊神经网络预测结果分析
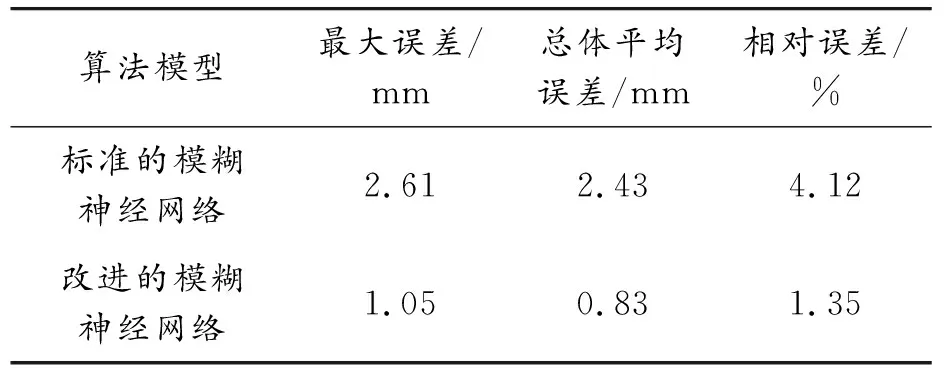
表2 2种预测模型误差情况
4 结论
针对校直机校直行程预测不准确的问题,提出一种改进型模糊神经网络来预测校直行程,并与标准模糊神经网络预测模型进行对比。分析发现,改进型模糊神经网络更适用于预测校直行程,预测结果更精确,总体平均误差仅为0.83 mm,实际值与预测值的相对误差为1.65%,验证了该模型的正确性,可将其运用于校直设备,为校直工艺提供参考。

