城市复杂环境下的车辆组合定位算法研究

朱 元,吴博宇,陆 科,吴名芝

(1.同济大学 汽车学院，上海 201800； 2.南昌智能新能源汽车研究院， 南昌 330052)

0 引言

近年来随着智能汽车技术的快速发展，车辆对于环境感知、定位、决策和规划控制等系统的要求愈发增高。其中，定位是一台自动车的必备基础，它需要告诉车辆相对于外界环境的精确位置，如果定位偏差过大，会引发车辆驾驶安全问题，严重的甚至会引发交通安全事故[1]。目前常用的车辆定位技术有：全球卫星导航系统(global navigation satellite system,GNSS)、惯性导航系统(inertial navigation system,INS)、视觉定位和激光雷达定位等。其中GNSS定位存在抗干扰能力弱、输出频率低的问题，而惯性导航自主性高且采样频率快，但长期精度差，将两者组合可以实现优势互补[2]。目前GNSS/INS组合定位作为一种主流的定位方案，在车辆导航定位领域得到了广泛应用。

城市环境是车辆最主要的工作环境，但城市环境的复杂性也给车载定位系统带来了巨大挑战。城市中随处可见的高楼、立交桥和树木等会导致卫星信号受到遮挡、多路径效应和非视距信号，从而导致GNSS系统的定位精度下降。由于目前多使用卡尔曼滤波作为GNSS/INS组合定位的主要方法，当GNSS信号出现异常时，若不能及时准确地对滤波参数进行修正，异常的GNSS测量值将导致组合定位系统的性能下降甚至发散[3]。

国内外学者为解决上述问题进行了大量研究，目前的研究方向之一为动态调节滤波器参数，主要是通过调节系统方差和量测方差，降低观测量异常对组合滤波器的影响[4]。一些学者使用改进的Sage-Husa自适应滤波算法，在进行状态估计的同时通过量测输出在线实时地估计系统的噪声参数，提高了系统的定位精度[5-7]。但Sage-Husa自适应滤波器对于突变工况的跟踪能力不足，在面对城市复杂工况时较难及时获得准确的噪声估计。还有学者使用数据驱动的方式进行滤波器参数的实时估计，如高斯过程[8]和支持向量机[4]等。但这类方法需要提前对模型进行训练，计算量较大。由于GNSS传感器除了可以得到计算后的定位信息外，还可以同时获得可观测卫星数量、位置精度因子(position dilution of precision,PDOP)、载噪比、卫星仰角等辅助信息，有学者提出采用上述信息进行卫星信号优劣的分类，如王加芳[9]对GNSS辅助信息的统计量构建检测方程进行阈值判断，将GNSS状态分为良好、异常和失锁三类；近年来，一些学者将上述信息作为输入，采用模糊推理系统(fuzzy inference system,FIS)进行传感器信号分类，进而实现对量测噪声的估计[10-11]。相比于采用阈值进行信号分类时界限分明的方式，模糊推理系统可以更为合理地确定测量信号所属类别并进行量测噪声的估计。但是由于模糊推理规则和隶属度函数需要人为设置，所以直接使用模糊推理系统得到的量测噪声估计会不可避免地引入人为误差。

为了提高城市环境下车辆组合定位系统的性能，本文在上述研究的基础上设计了一种基于模糊自适应卡尔曼滤波的车辆组合定位算法，滤波方法选用误差状态卡尔曼滤波，将GNSS的辅助信息作为模糊推理系统的输入，系统的输出作为量测噪声协方差的先验调整系数，通过改进的Sage-Husa自适应滤波算法对量测噪声进行自适应估计，同时辅以车辆运动约束。通过计算机仿真与实车实验对算法性能进行了验证，结果表明：提出的算法在保持了对突变工况的跟踪能力的同时，在GNSS异常区域可以获得较高的定位精度。

1 GNSS/INS组合定位系统

1.1 GNSS/INS组合定位模型

对于GNSS/INS组合定位系统，本文使用误差状态卡尔曼滤波[12](error state Kalman filter，ESKF)作为滤波的方法，将系统的真实状态分为名义状态和误差状态两类：

xt=x⊕δx

(1)

其中,名义状态向量x共16维，分别为东北天向的位置、速度、方位四元数以及加速度计和陀螺仪的三轴偏差；误差状态向量δx共15维，分别为东北天向位置误差、速度误差、旋转向量误差以及加速度计和陀螺仪的三轴测量偏差的误差，分别表示如下：

x=[pvqabwb]T

(2)

δx=[δpδvδθδabδwb]T

(3)

对于名义状态，其递推方程为：

(4)

(5)

(6)

对于误差状态，当旋转向量误差δθ定义在世界坐标系下时，其递推方程如式(7)所示。其中vi、θi、ai、wi为符合高斯分布的零均值白噪声，其方差分别写作Vi、Θi、Ai、Ωi，则系统噪声矩阵表示为式(8)。

(7)

(8)

系统的名义状态转移函数f可由式(4)确定，误差状态转移矩阵Φδ,k/k-1和系统噪声分配矩阵Γ可由式(7)确定。综上，系统预测方程表示如下：

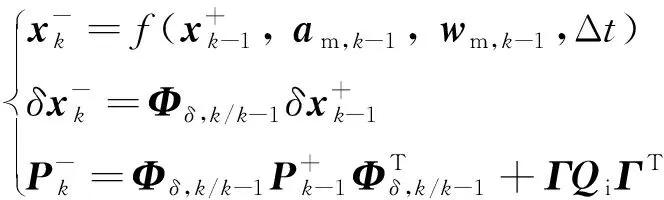
(9)

在GNSS/INS组合定位中，将GNSS的位置信息作为观测量：

Z=[xyz]T

(10)

则量测矩阵：

(11)

系统的量测更新方程为：

(12)

(13)

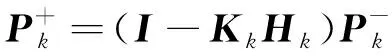
(14)

系统状态更新完成后需要将名义状态和误差状态合并，并将误差状态参数重置：

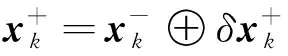
(15)

(16)

其中，当旋转向量误差δθ定义在世界坐标系下时，方位四元数的合并式及方差重置矩阵Gk分别为：

(17)

(18)

1.2 车辆运动约束在GNSS/INS定位中的应用

考虑到车辆在正常行驶状态下，其相对载体坐标系的侧向和纵向速度均应为0，故对于城市车辆的GNSS/INS组合定位系统，可以利用车辆运动约束对模型进行修正[13]，据此构建观测量：

Z′=[vyvz]T=[0 0]T

(19)

则量测矩阵表示为：

(20)

其中：

(21)

之后利用式(12)—(16)进行系统的量测更新、状态合并以及参数重置，实现运动约束对组合定位系统的修正。

2 基于模糊自适应卡尔曼滤波的城市车辆组合定位方法

对于GNSS/INS组合定位系统，标准的ESKF算法在整个滤波过程中将式(12)中的量测噪声协方差Vk设置为固定值，在理想工况下可以取得较好的定位结果，但是在城市复杂环境中GNSS的真实量测噪声会发生显著变化，若不能及时准确地对Vk进行修正，异常的GNSS测量值将导致系统的定位精度下降。

针对这一问题，提出了一种基于模糊自适应卡尔曼滤波的城市车辆组合定位方法，在前述添加了车辆运动约束的GNSS/INS组合定位系统的基础上加入量测噪声模糊自适应估计模块，将模糊推理系统与改进的Sage-Husa算法相结合，在保证对系统突变工况的跟踪能力的同时提升系统在GNSS异常区域的定位精度。基于模糊自适应卡尔曼滤波的城市车辆组合定位方法的完整结构如图1所示。

图1 基于模糊自适应卡尔曼滤波的城市车辆组合定位方法结构框图

图1中虚线框部分为量测噪声模糊自适应估计模块，使用模糊推理系统监测GNSS提供的辅助信息(卫星数量N和PDOP)并输出量测噪声调整系数tk作为先验信息，之后利用基于改进Sage-Husa算法的量测噪声自适应估计算法对量测噪声进行估计，下面对该模块进行具体介绍。

2.1 基于模糊推理系统的量测噪声估计

模糊推理系统又称为模糊系统，它以模糊逻辑理论为主要计算工具，由模糊化、模糊规则库、模糊推理方法以及去模糊化几部分组成，其输入输出都是精确值，可用于GNSS量测噪声的估计。现有研究表明，可观测卫星数量N和卫星的PDOP值可以用于场景的区分[4]，将其作为FIS的输入，量测噪声协方差调整系数tk作为输出实现GNSS量测噪声的调整，FIS的结构如图2所示。

图2 FIS结构框图

根据经验，将N、PDOP和tk分别划分为3个模糊集，并使用合适的隶属度函数对其进行描述，如图3—5所示(若卫星数量小于4颗，认为此时GNSS的定位结果不可用，在GNSS/INS组合定位中需要切断GNSS的输入，故设计隶属度函数时将这种情况忽略)。

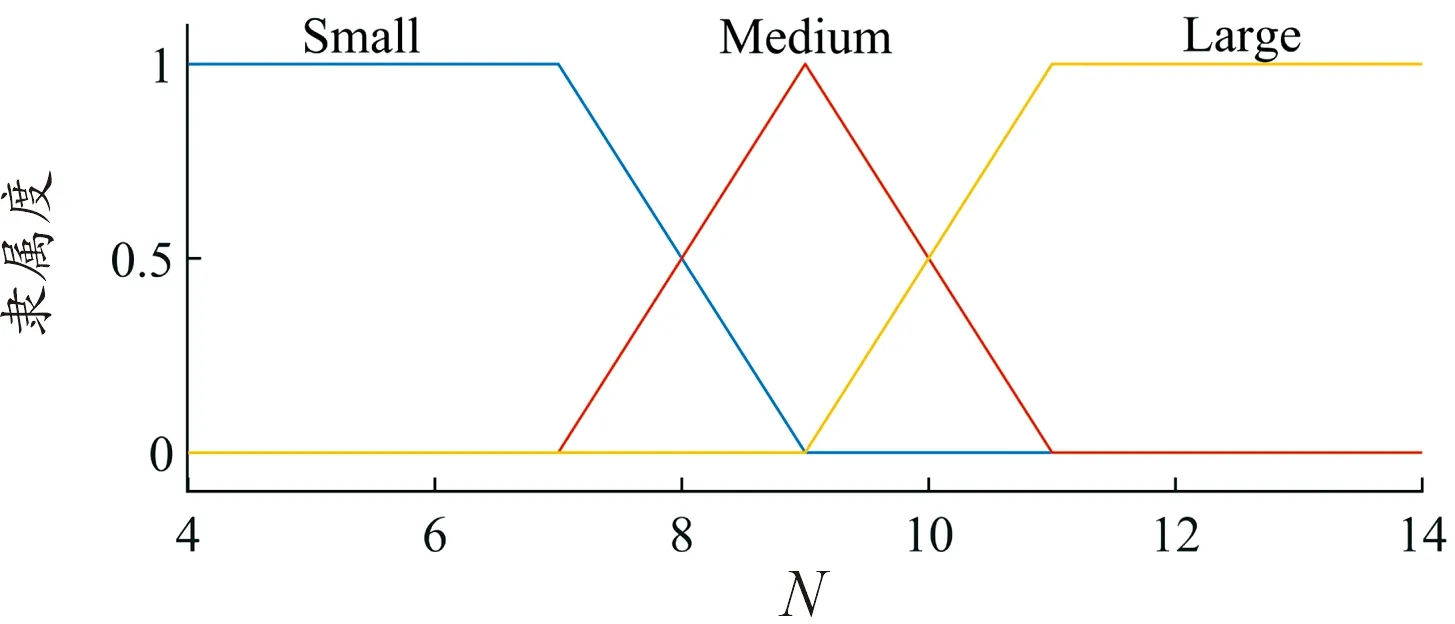
图3 卫星数量N隶属度函数曲线

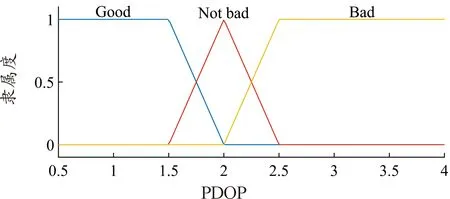
图4 PDOP隶属度函数曲线

考虑到当车辆行驶到GNSS信号异常区域时，可观测卫星数量会明显减少，与此同时PDOP值显著增大，GNSS的定位误差增大[4]，据此设计模糊推理规则，如表1所示。

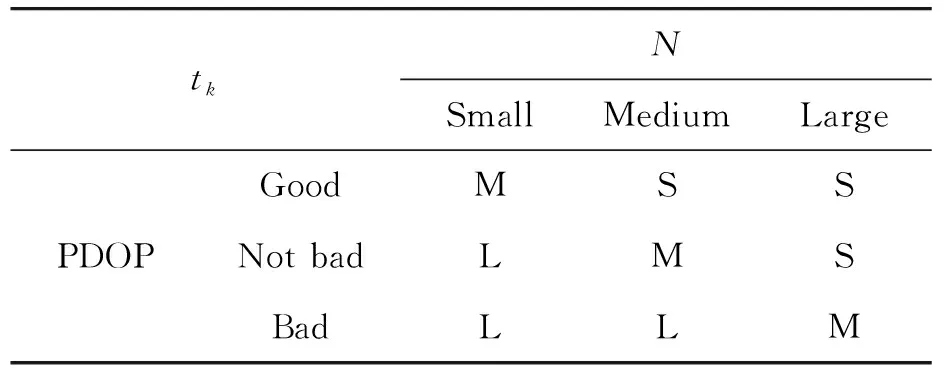
表1 模糊推理规则

分别选用Mamdani法和重心法作为FIS中的模糊推理方法和去模糊化方法，得到的输入输出关系如图6所示。利用FIS对GNSS提供的辅助信息进行实时监测，输出的量测噪声协方差调整系数tk可用于对量测噪声进行调整，将式(12)进行改写，如式(22)所示。

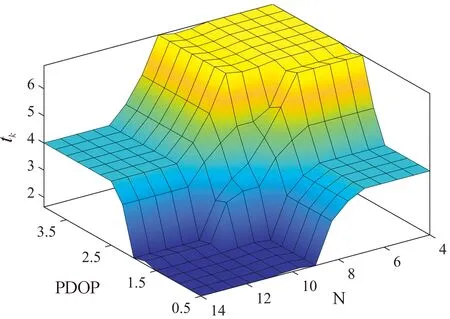
图6 FIS的输入输出特性曲面

(22)

式中：V0为良好工况下量测噪声协方差的参考值。使用FIS对量测噪声进行调整可以使系统获得对突变工况的跟踪能力，但直接使用其进行量测噪声的估计会不可避免地引入人为误差。现将FIS的输出结果作为先验信息，利用改进的Sage-Husa算法对量测噪声进行估计。

2.2 基于Sage-Husa算法的量测噪声自适应估计

除可以利用传感器辅助信息进行组合定位系统的噪声估计外，系统模型预测值与传感器观测值之差(一般称为新息)也可以用于表征系统的噪声水平，其中一种使用较广泛的算法为Sage-Husa自适应滤波算法，该算法可以在进行系统状态估计的同时利用时变噪声统计估计器对量测噪声参数和系统噪声参数进行实时在线估计和修正。但现有的研究发现，对所有的噪声参数进行准确估计很难实现，实际研究中最常用也比较有效的是一种对Sage-Husa算法改进的量测噪声方差阵自适应算法[14]。

在卡尔曼滤波中，新息表示为：

(23)

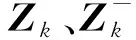
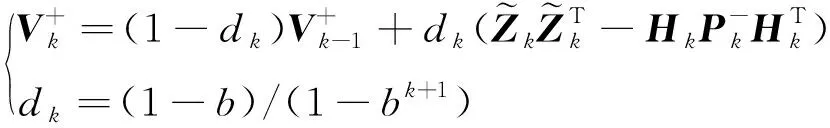
(24)

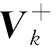
(25)

对于第i个分量，记：

(26)

(27)

改进的Sage-Husa算法在保证较高的滤波精度的同时减少了计算量，但在面对突变工况时无法及时准确地进行量测噪声估计，使用FIS的输出作为先验信息进行量测噪声自适应估计可以有效解决这一问题。

将tk映射到[0,1]区间上：

(28)

构造量测噪声跳变参数：

Δαk=|αk-αk-1|

(29)

当检测到量测噪声跳变参数较大时，可以认为车辆所处环境发生较大变化，当前的量测噪声存在较大误差，需要及时进行调整，首先利用式(22)进行量测噪声的快速修正，之后使用改进的Sage-Husa算法对量测噪声进行估计。综合考虑算法突变工况的跟踪能力、算法的稳定性以及计算量，引入自适应跟踪参数m、跳变检测阈值ηΔα和自适应窗口阈值n0，分别用于根据突变程度的大小调整对突变工况的跟踪强度、环境改变的检测以及自适应窗口的长度限定；同时，若检测到连续多帧α小于阈值ηα，则使用初始V0作为量测噪声协方差，以用于环境良好工况下的组合定位系统。

综上所述，基于改进Sage-Husa算法的量测噪声自适应估计算法流程如图7所示。

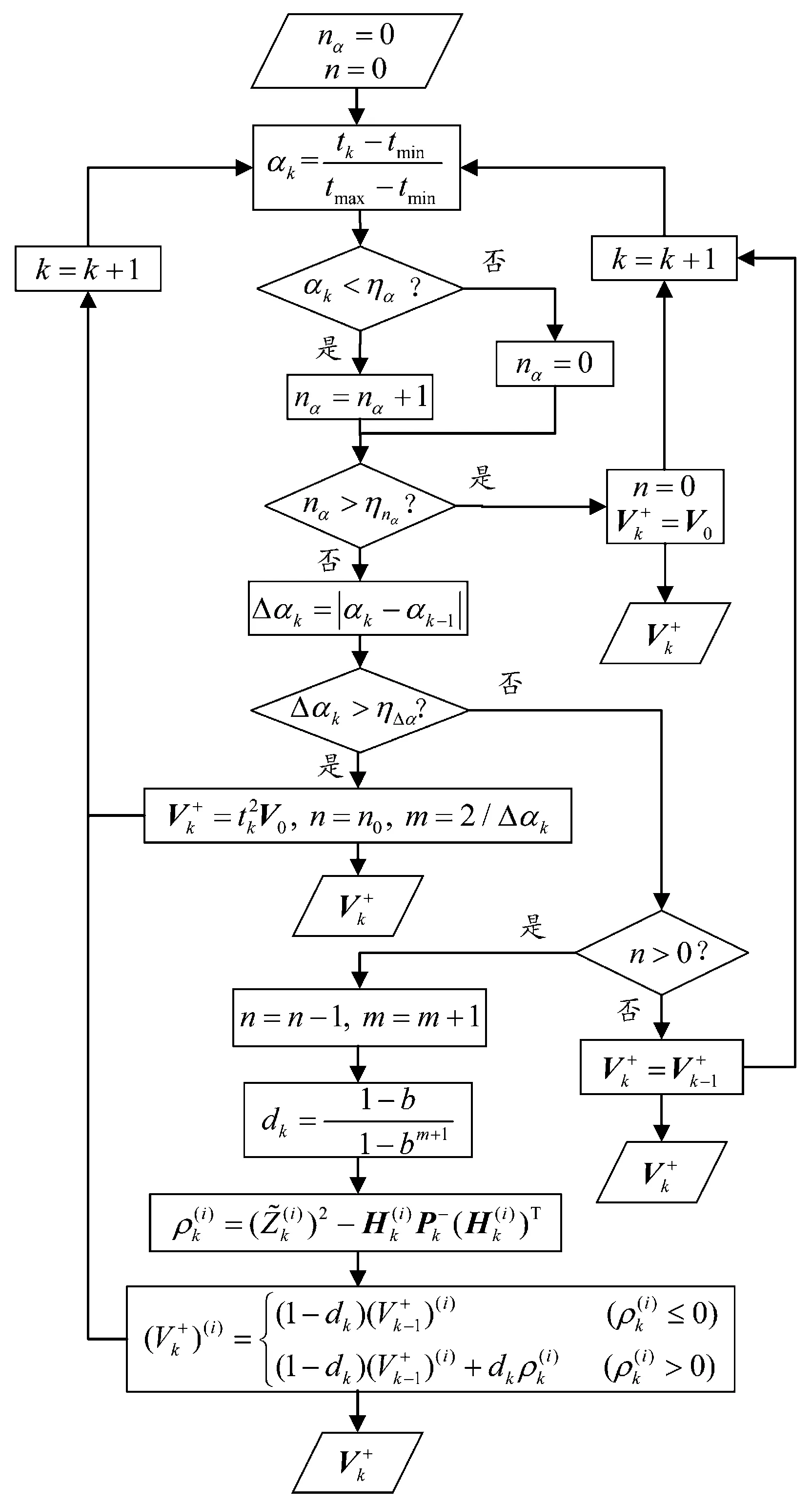
图7 基于Sage-Husa算法的量测噪声自适应估计算法流程框图

3 实验与结果分析

3.1 仿真实验与结果分析

为验证算法的有效性，基于Matlab平台进行仿真测试，假设车辆从原点出发，向东北方向以5 m/s的速度匀速运动，仿真时长240 s。参考真实传感器手册参数，将仿真环境的传感器参数设置为：惯性测量单元相关参数如表2所示，采样频率100 Hz；GNSS采样频率设置为1 Hz，0～100 s及150～240 s的GNSS水平位置误差0.5 m，可观测卫星数量N为14，PDOP为1.5，模拟GNSS信号良好环境；100～150 s模拟车辆进入GNSS信号异常区域，GNSS水平位置误差设置为4 m，N和PDOP分别为8和2.5，仿真轨迹及GNSS定位结果如图8所示。在其他参数完全一致的条件下，分别使用标准ESKF算法、改进的Sage-Husa自适应滤波算法(记作SHAESKF)、仅使用FIS进行量测噪声估计的模糊卡尔曼滤波算法(记作FESKF)以及本文中提出的基于量测噪声模糊自适应估计的模糊自适应卡尔曼滤波算法(记作FAESKF)对上述仿真数据进行处理，不同算法在GNSS异常区域的定位结果如图9、10所示。

表2 惯性测量单元参数

图8 仿真轨迹及GNSS定位结果曲线

图9 不同算法在GNSS异常区域的定位结果曲线

图10 不同算法在GNSS异常区域的定位结果曲线(局部放大)

在GNSS信号良好区域行驶一段时间后，使用不同算法均能得到较好的定位结果，但进入GNSS信号异常区域后，不同算法的定位效果出现较大差异。对不同算法在GNSS信号异常区域的定位效果进行统计，结果如表3、图11所示。

表3 不同算法的定位误差

图11 不同算法的定位误差曲线(异常区域)

同时，对几种算法在GNSS异常区域的量测噪声方差估计值进行统计，如表4所示。

表4 量测噪声方差估计平均值

由图10(a)可知，在车辆进入GNSS信号异常区域时，使用标准ESKF算法和SHAESKF算法的组合定位方案均受到异常值的影响出现轨迹漂移；由图10(d)可知，基于SHAESKF算法的定位方案在车辆重新进入GNSS信号良好区域时仍需较长时间才能恢复准确的定位结果；而基于FESKF算法和FAESKF算法的组合定位方案能够对突变工况进行及时跟踪。同时，综合分析上述仿真结果可知，在GNSS信号异常区域，本文中提出的基于量测噪声模糊自适应估计的模糊自适应卡尔曼滤波算法可以修正模糊推理系统存在的误差，对量测噪声进行较为准确地估计，在保证了对突变工况跟踪能力的同时，可以获得较高的定位精度。

3.2 实车实验与结果分析

3.2.1实验设计

为进一步验证所提算法的有效性，使用搭载车规级六轴惯性测量单元IAM-20680和u-blox M8型GNSS模块的实验车辆在同济大学嘉定校区内进行了实车实验，车辆行驶路线如图12所示，图中的框线区域为仰望星空大楼，车辆在该大楼下通过时GNSS信号会出现异常，大楼的结构如图13(a)所示。

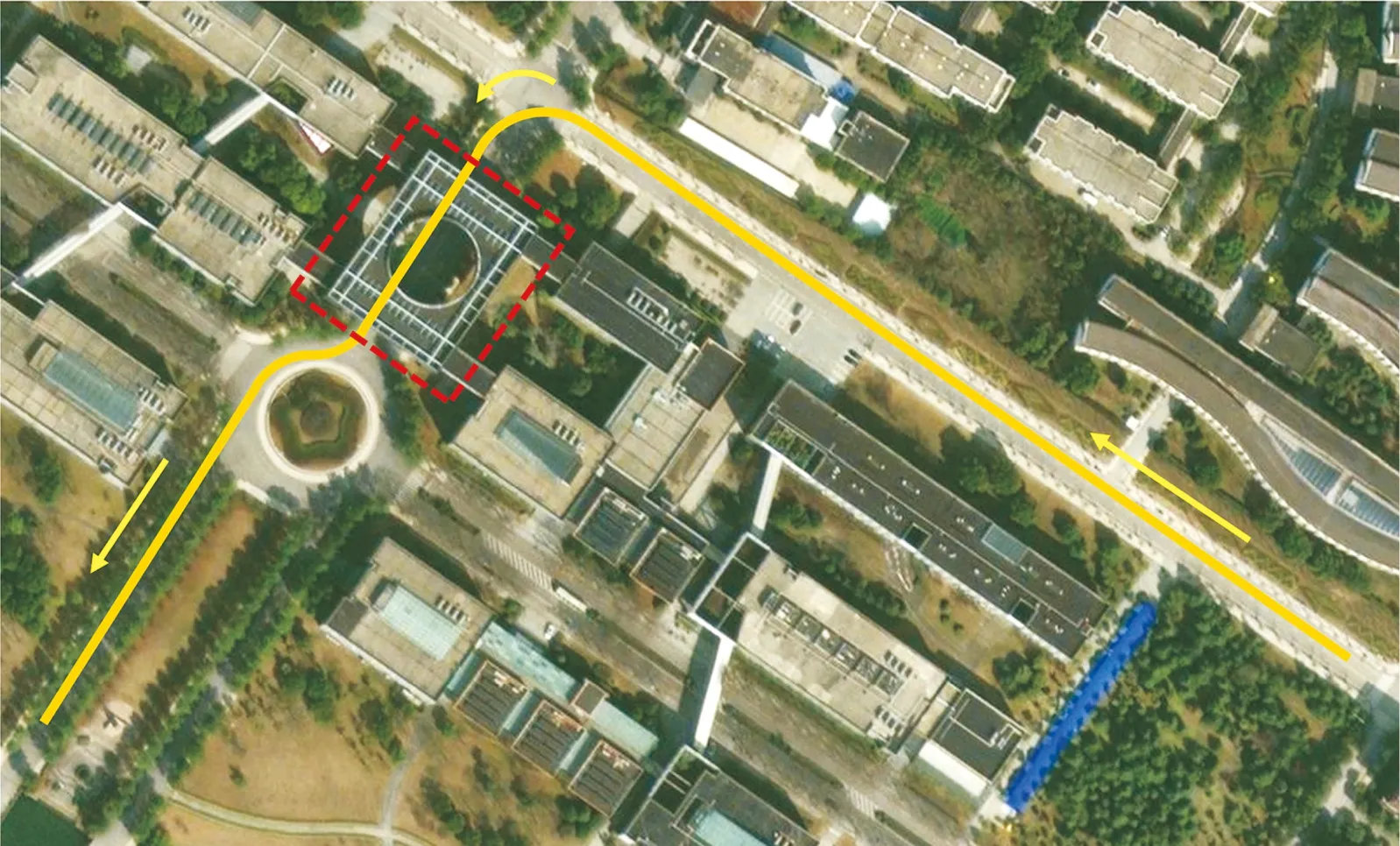
图12 车辆的行驶路线场景

同时，为了对算法的定位效果进行评判，使用超宽带(ultra wide band，UWB)定位设备的定位结果作为车辆行驶轨迹的参考(实验前对该区域的UWB定位精度进行了测试，结果表明定位误差在10 cm以内，可以作为车辆行驶轨迹的参考值)，仰望星空区域的UWB基站布置方式如图13(b)所示。同时，使用高精度RTK设备对测试区域附近开阔环境基准点的经纬度进行测量，并计算出UWB基站在大地坐标系下的位置，从而实现UWB局部坐标系与大地坐标系的统一。

图13 实验环境场景及基站布置示意图

3.2.2实验结果与结果分析

分别使用ESKF算法、加入运动约束的ESKF算法(记作ESKF+KC)以及本文中提出的基于模糊自适应卡尔曼滤波的城市车辆组合定位算法(记作FAESKF+KC)对采集的数据进行处理，结果如图14所示。

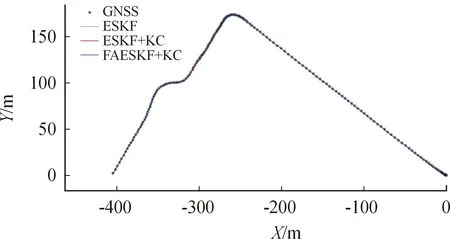
图14 不同算法的定位结果曲线

在GNSS良好区域，不同算法得到的定位结果差别不大，但进入GNSS异常区域后，不同算法的定位效果出现较大差异，GNSS异常区域的卫星定位结果及使用不同算法进行数据处理得到的定位结果分别如图15、16所示。将不同算法得到的定位结果与车辆的参考行驶轨迹进行比较，得到不同算法在GNSS异常区域下的平均定位误差，如表5所示。

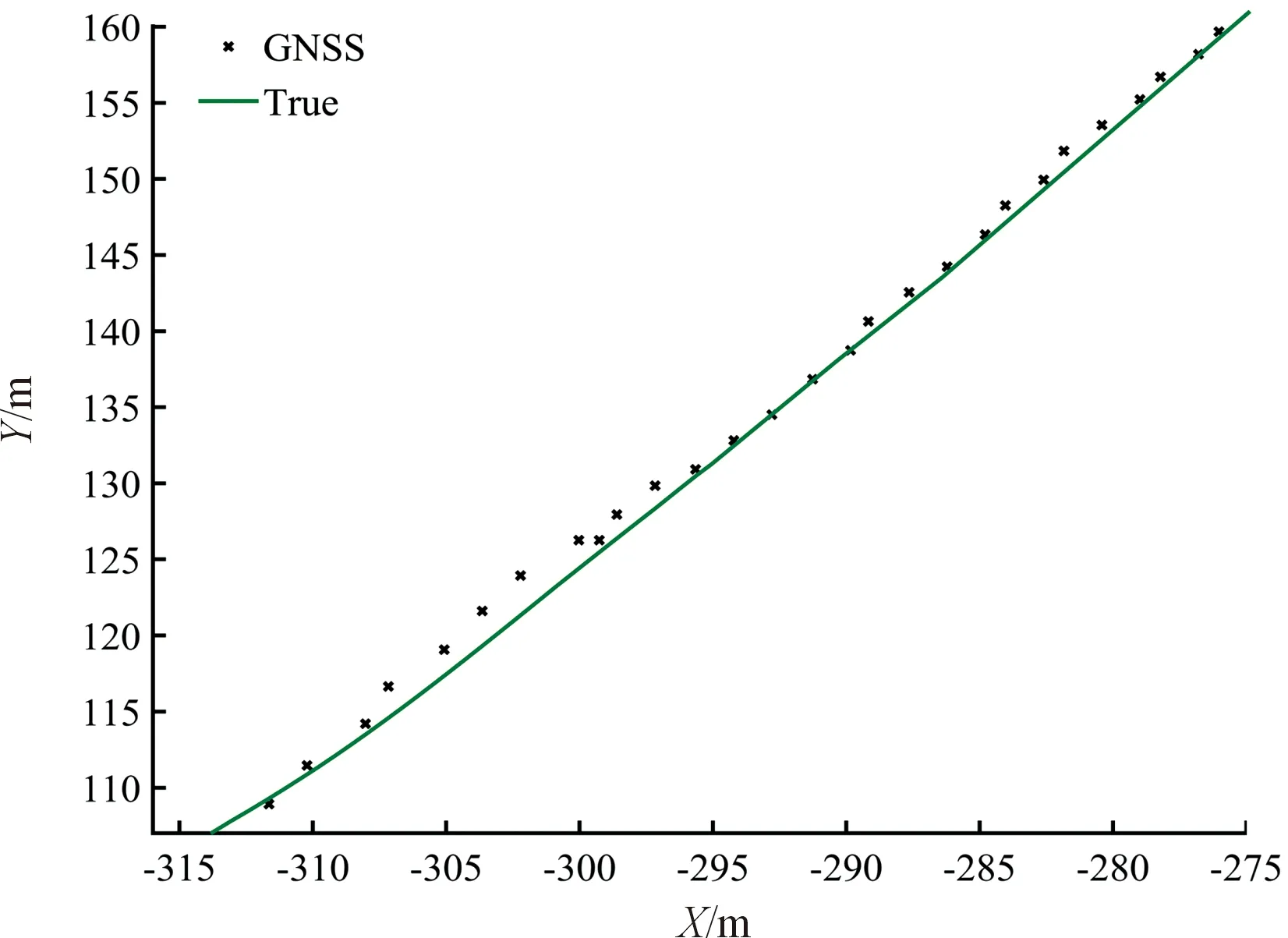
图15 GNSS异常区域的定位结果曲线

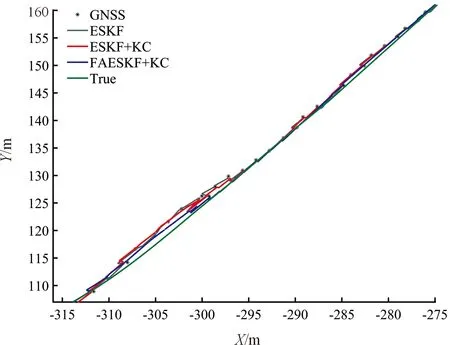
图16 不同算法在GNSS异常区域的定位结果曲线

表5 不同算法的定位误差

实验结果表明，基于模糊自适应卡尔曼滤波的城市车辆组合定位方法通过量测噪声的模糊自适应估计和车辆运动约束对模型误差进行了有效修正，在GNSS异常区域仍能够获得较为准确的定位结果，平均定位误差相比于标准的ESKF方法减少了0.479 m，平均定位精度提高了41.8%。

4 结论

针对城市环境下车辆组合定位系统的需求，提出了一种基于模糊自适应卡尔曼滤波的车辆组合定位算法，综合利用GNSS提供的辅助信息以及滤波过程中的新息向量对量测噪声进行及时调整，同时辅以车辆运动约束对模型误差进行修正，提高了系统的定位精度。通过计算机仿真和实车实验对所提算法进行验证，结果表明，提出的算法能够及时有效地对量测噪声进行调整，在GNSS信号异常区域仍可以保持较高的定位精度，能有效解决城市环境中车辆的定位问题。