水下采油树S密封结构优化与试验研究*

张崇 余意 黄亮 董钊 张红 冯定

(1.中海石油(中国)有限公司湛江分公司 2.长江大学机械工程学院 3.湖北省油气钻完井工具工程技术研究中心)

0 引 言

随着油气钻采深度越来越深，现存油气藏的开采工艺要求越来越高，井口压力也由初始的34 MPa剧增至目前将近69 MPa，传统的橡胶弹性体加挡圈的密封组合只能满足常规的井下压力和温度。为了使水下采油树能够应用于69 MPa的介质压力以及180 ℃以上的高温高压环境[1]，设计了一种专为满足目前石油天然气行业所面临的高温、高压和复杂流体介质工况的特殊密封件——S密封。S密封是一种带有弹簧的非金属密封，弹簧所用材料是316不锈钢，弹性体材料是氢化丁腈橡胶。因其材料性能使得S密封具有良好的耐腐蚀性，耐高压性以及较好的弹性变形能力，目前已广泛应用于高温高压容器中。

目前对于非金属密封的研究比较多。潘雅琼[2]建立唇形密封圈的二维轴对称有限元模型，研究了油侧温度对唇口温度的影响情况，通过几何结构参数的灵敏度分析，优化密封唇口的接触应力分布。尚付成等[3]利用非线性有限元ABAQUS软件，分析了弹性体密封在高压下的von Mises应力和密封面接触应力的分布，分析了不同压缩率及密封间隙对密封结构最大von Mises应力与密封面最大接触应力的影响。周志鸿等[4-5]利用有限元ANSYS软件对弹性体密封在不同压缩率和油压下的变行与受力情况进行了分析研究。田懿等[6]采用二维弹塑性有限元法，对应用于水下采油树油管悬挂器的K形金属密封在不同压缩量、不同介质压力和温度时的von Mises应力分布及接触压力分布进行数值模拟，确定了密封材料易失效部位和有效密封面区域。陶玉瑾等[7]利用仿真模拟研究了非金属MEC密封圈的各个结构参数对其结构强度和密封性能的影响规律，确定了影响显著的结构参数。

但是以S密封为研究对象进行研究的文献很少。为此，笔者在前人研究非金属密封的基础上，基于有限元法和响应面法，考虑弹性体和弹簧的主要结构尺寸对密封性能的影响，得到S密封结构参数对强度和性能的规律，并对S密封的强度和密封性能进行优化。

1 密封机理与装载过程

S密封由于内侧的过盈，使得内密封面与沟槽底面紧密接触，如图1a所示。在沟槽与密封圈下移的过程中，由于密封圈外侧的过盈量，使得外密封面与被密封面紧密贴合，实现了密封圈的预密封，如图1b所示。当流体通过间隙进入沟槽时，对S密封的一侧面起作用，将密封圈挤压成近似矩形，并将压力传递给密封面实现密封，如图1c所示。相较于普通橡胶密封圈，由于S密封存在两弹簧，可以防止在高压环境下密封胶料的挤出，保证其在高压环境下的密封效果。

图1 S密封密封机理Fig.1 Sealing mechanism of the S-seal

2 S密封仿真分析

2.1 有限元模型建立

本文以油管悬挂器处非金属S密封研究对象建立有限元模型。为了研究S密封结构参数对密封性能的影响，选取了S密封的截面高度、截面宽度、弹簧直径和圆弧半径作为研究的结构参数，如图2所示。S密封截面高度、截面宽度、弹簧直径、圆弧半径分别采用符号A、B、C、D表示，其初始取值分别为13、7、3和4 mm。

图2 S密封结构参数示意图Fig.2 Schematic diagram of S-seal structural parameters

由于三角网格对复杂图形有较好的适应性且更易对图形进行局部加密，所以弹簧和弹性体部分均采用三角形网格划分。通过网格无关性验证[8]，整个模型的尺寸取0.1 mm，局部加密网格尺寸取0.05 mm，节点总数为51 851，网格单元总数为25 132。

2.2 材料参数设置

S密封弹簧采用316不锈钢，这是一种奥氏体不锈钢，质地较软，因添加了钼，其耐腐蚀性和高温强度均较好，通常在高温高压环境下使用。其密度为8.03×103kg/m3，弹性模量为195 GPa，泊松比为0.3，屈服强度为310 MPa。

S密封弹性体采用氢化丁腈橡胶(HNBR)，是一种对丁腈橡胶进行特殊加氢处理的高饱和超弹性体。橡胶材料具有高度非线性，体现在材料非线性、接触非线性和几何非线性。S密封在采油树中属于中小变形，因此选用Mooney-Rivlin模型来描述橡胶材料的应变能函数[9-10](应力与应变的关系函数)，其表达式为：

W=C10(J1-3)+C01(J2-3)+C20(J1-3)2+

C11(J1-3)(J2-3)+C02(J2-3)2+C30(J1-3)3+

C21(J1-3)2(J2-3)+C12(J1-3)(J2-3)2+

C03(J2-3)3+K(J3-1)2/2

(1)

式中：W为应变能；C10～C03为Mooney-Rivlin模型材料力学性能参数；J1、J2、J3为应力张量第1、第2、第3的缩减不变量；K为修正系数，K=6(C10+C01)/[3(1-2μ)]；μ为泊松比。

9参数的Mooney-Rivlin非线性模型应力应变关系[11]模拟曲线如图3所示。图3中，unia表示单轴拉伸试验应力与应变关系，biax表示双轴拉伸试验应力与应变关系，shea表示剪切试验应力与应变关系。

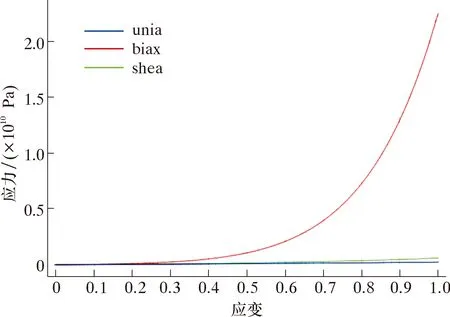
图3 氢化丁腈橡胶应力与应变模拟曲线Fig.3 Simulated stress vs.strain of HNBR

2.3 接触设置

被密封面与密封圈的接触属于弹性体-刚体的面面接触，在设置接触算法和类型时，根据实际工程中，S密封中橡胶存在材料、几何和结构复杂非线性因素，最终采用接触单元的拉格朗日函数算法进行分析[12-15]。设定S密封与沟槽内壁和外被密封件之间为摩擦接触，摩擦因数设置为0.2，由于弹簧与弹性体为一体，将弹簧与弹性体的接触设为绑定接触。

2.4 边界条件和加载

为了使得到的数据更加符合实际工作状态，将有限元分析设置为2步骤：第1步通过内、外被密封件的位移挤压密封圈，模拟密封圈初始预紧的过盈量，过盈量大小为2.265 mm；第2步在密封圈的高压侧加载介质压力，模拟油气介质对密封圈的影响，介质压力最大为69 MPa。约束与加载如图4所示。在分析时，由于S密封主要由橡胶构成，需要打开弱弹簧和大挠曲才能保证运算准确。

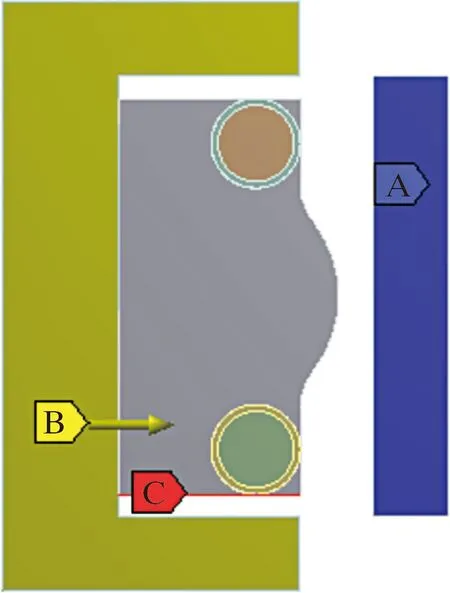
图4 S密封约束与载荷设置Fig.4 Constraints and load on the S-seal

2.5 结构参数对密封性能影响规律

等效应力反映密封圈结构可靠性，要防止等效应力过大从而出现密封圈破坏；接触应力反映了密封圈的密封性能[16-19]。选择S密封的4个主要结构参数，分别为S密封截面高度、截面宽度、弹簧直径、圆弧半径，取值范围为：截面高度取11～15 mm，截面宽度5.6～8.4 mm，弹簧直径2.4～3.6 mm，圆弧半径3.2～4.8 mm，分别研究它们对密封圈结构强度和密封性能的影响规律；利用有限元分析得到各结构参数对密封圈等效应力和内、外接触应力影响，结果如图5～图8所示。

图5 截面高度与应力关系Fig.5 Section height vs.stress

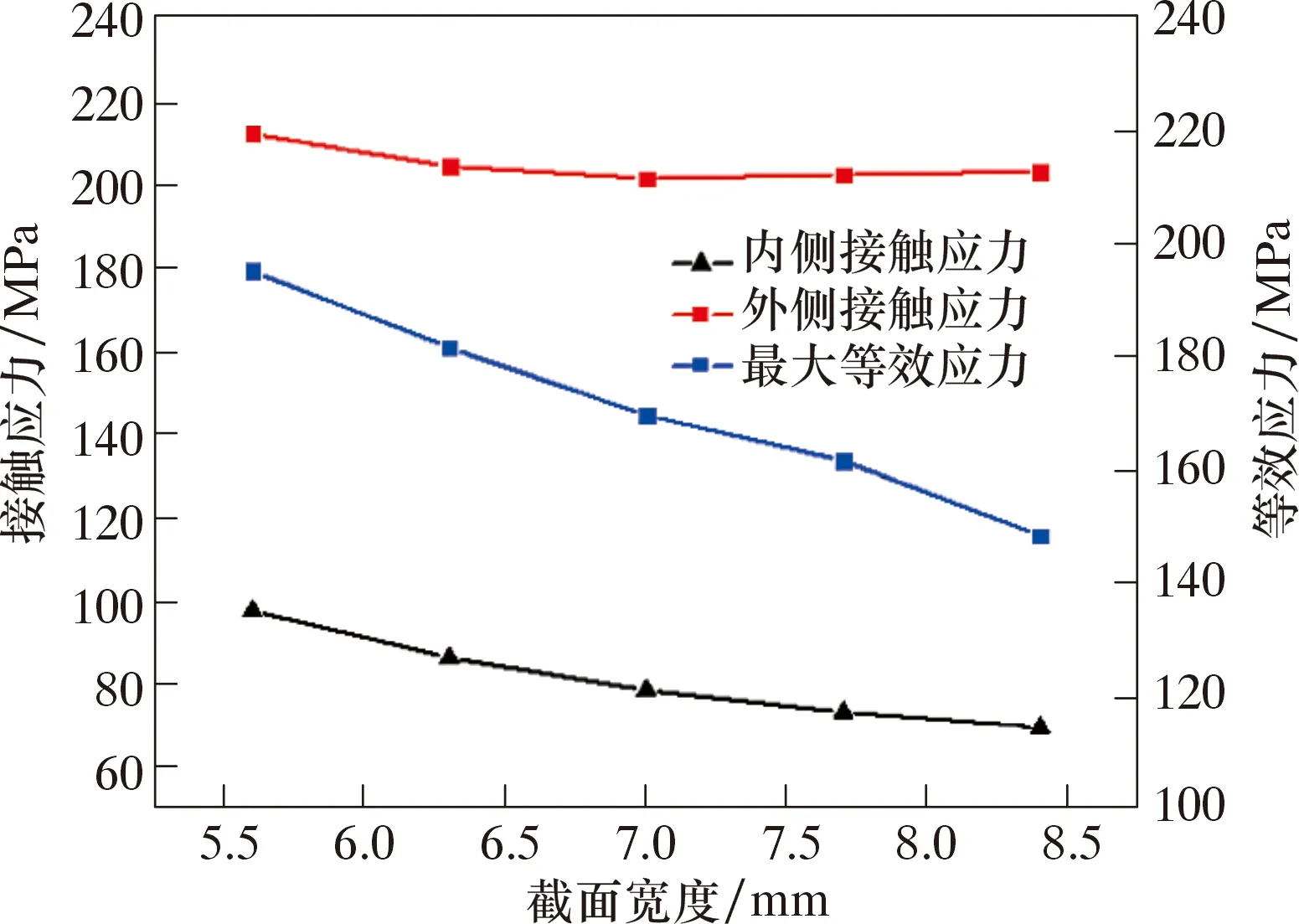
图6 截面宽度与应力关系Fig.6 Section width vs.stress

图7 弹簧直径与应力关系Fig.7 Spring diameter vs.stress

图8 圆弧半径与应力关系Fig.8 Arc radius vs.stress

从图5～图8可以看出：随着截面高度和弹簧直径的增加，密封圈最大等效应力先减小后增大；随着截面宽度的增加，最大等效应力呈线性减小趋势；随着圆弧半径的增加，最大等效应力呈较缓趋势增加。

随着截面高度和截面宽度的增加，内侧接触应力与外侧接触应力均呈平缓减小趋势；随着弹簧直径的增加，内侧接触应力逐渐减小，外侧接触应力逐渐增加；随着圆弧半径的增加，内侧接触应力小幅度增加，外侧接触应力较大幅度减小。

3 S密封结构优化

3.1 响应面试验设计

根据上述单因素分析的结果，4个结构参数都具有较高的敏感性，故选择这4个因素生成S密封结构尺寸4因素3水平试验表，如表1所示。

表1 S密封结构尺寸因素水平Table 1 Levels of the S-seal structural dimensions

根据因素水平表，运用响应面分析软件生成响应面分析表，共需对29组不同结构组合的S密封进行仿真分析，选取15组最具有代表性的响应面分析设计方案及仿真分析结果，如表2所示。

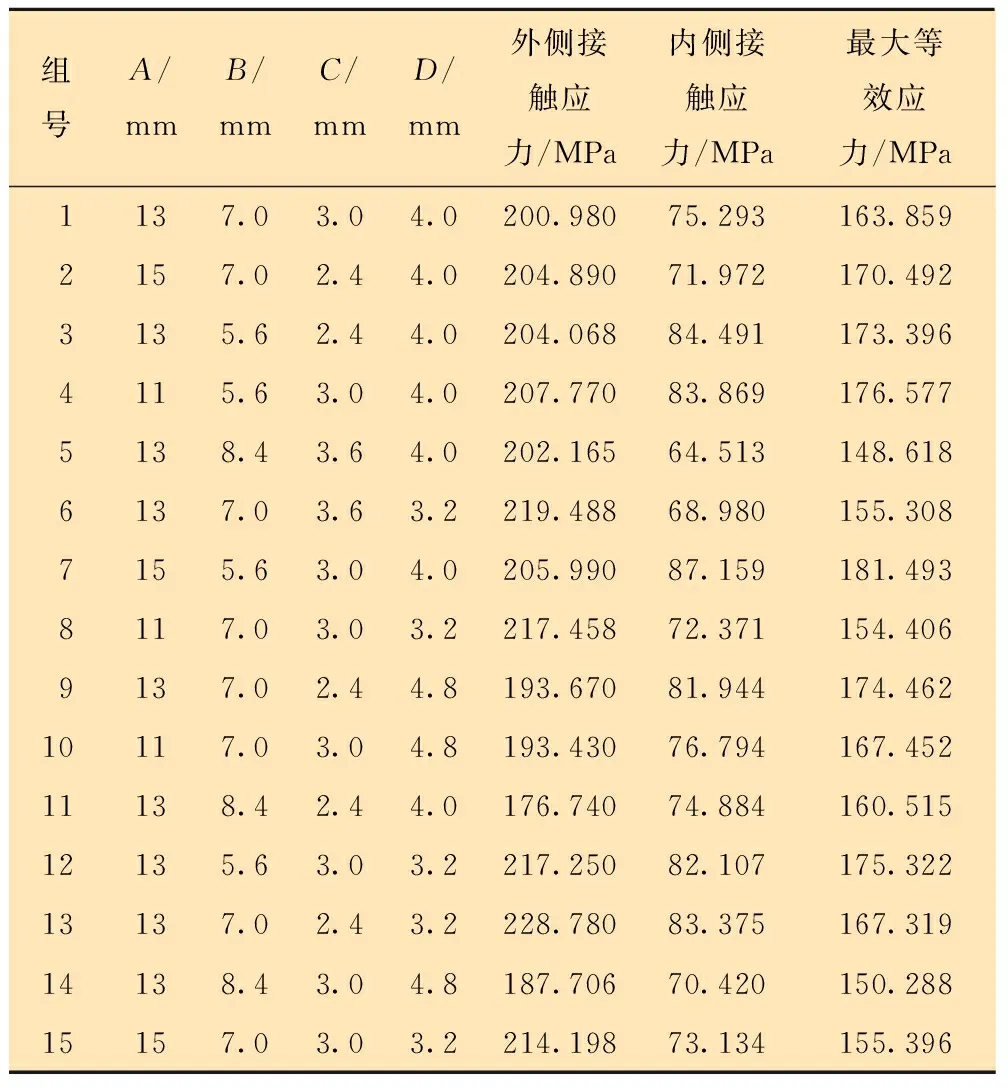
表2 响应面分析设计方案及结果Table 2 Scheme and results of the response surface analysis

根据数据得到应力多项式回归方程如下：

Y1=736.66-20.67A-10.09B-112.64C-
77.601D+0.24AB+3.8AC+0.35AD+
5.88BC-0.17BD+5.01CD+0.25A2-
0.96B2+0.47C2+5.44D2

(2)

Y2=320.15-18.71A-0.40B-15.76C-41.62D+0.09AB+2.36AC+2.14AD-2.58BC-1.52BD+3.39CD+0.12A2+0.57B2-2.62C2+2.18D2

(3)

Y3=513.62-44.19A+16.10B-74.97C+11.20D+0.08AB+3.39AC+1.95AD-3.35BC-2.35BD+0.19CD+0.99A2-0.38B2+7.57C2-1.20D2

(4)

式中：Y1为外侧接触应力；Y2为内侧接触应力；Y3为最大等效应力；A为截面高度；B为截面宽度；C为弹簧直径；D为圆弧半径。

3.2 响应面分析

为了检验二阶响应面模型是否可以真实有效地反映设计变量与响应变量间的规律，需要对回归方程进行方差分析。表3为回归方程的方差分析表；表4为回归方程误差统计分析表[20]。

由表3可知：建立的外侧接触应力模型P值为0.007 3<0.01，失拟项的P值为0.071 2>0.05；建立的内侧接触应力模型P值为0.001 2<0.01，失拟项的P值为0.092 4>0.05；建立的最大等效应力模型P值为0.008<0.01，失拟项的P值为0.079 9>0.05。证明所构建的二阶响应面模型拟合度较高，可以较为真实有效地反映设计变量与响应变量之间的规律。

表3 回归方程的方差分析表Table 3 Variance analysis of the regression equation

从表4可以看出：变异系数CV均小于5%，证明了试验观测值的离散程度较小，试验数据的精确度较好；多元相关系数R2的值均接近1，表明各因素之间相关性强；调整R2和R2预测值基本接近于1，其中最大等效应力R2预测值差值为0.002 8，说明预测值与模拟值很接近。从表4还可以看出，通过响应面分析软件进行二次多项式回归分析所拟合的回归方程的各误差统计项目的值均满足其各项检验原则。

表4 回归方程误差统计表Table 4 Statistics of errors of the regression equation

响应面曲面可较直观地反映各因素及两两因素交互作用对响应值的影响。选取密封圈外侧最大接触应力的三维响应曲面，如图9所示。

图9 外侧最大接触应力三维响应面Fig.9 Three-dimension response surfaces of the outside maximum contact stress

图9a为截面高度与宽度的交互，二者交互作用对外侧最大接触应力影响较小；图9b为截面高度与弹簧直径的交互，截面高度由11 mm增加到15 mm，外侧最大接触应力值随弹簧直径增大而小幅度减小；图9c为截面高度与圆弧半径的交互，截面高度由11 mm增加到14 mm，外侧最大接触应力值随圆弧半径增大而较大幅度减小；图9d为截面宽度与弹簧直径的交互，截面宽度由5.6 mm增加到7.0 mm中，外侧最大接触应力随弹簧直径增大而增大；图9e为截面宽度与圆弧半径的交互，图9f为弹簧直径与圆弧半径的交互，两两的交互作用对外侧接触应力影响均较大，主要体现在圆弧半径的影响。

综上，密封圈圆弧半径与各因素交互作用对外侧最大接触应力影响最大，其次是弹簧直径，截面高度与截面宽度交互作用对外侧最大接触应力的影响最小。

3.3 结构优化

在响应面分析软件中，以目标响应值即等效应力最小、接触应力最大为优化目标进行优化求解，软件以构建的响应面近似模型为求解函数，计算出了满足优化目标的S密封优化结构尺寸。为了验证优化后S密封性能更优，通过有限元建立了S密封优化前、后尺寸模型，计算了优化前、后S密封在工作状态下等效应力和接触应力，结果如表5所示。

表5 优化前后S密封参数与响应值对比Table 5 Parameters and mechanical responses of the S-seal before and after optimization

由表5可知，最后通过响应面软件得到了S密封结构尺寸的最优值为截面高度为13 mm、截面宽度为5.6 mm、弹簧直径为2.7 mm、圆弧半径为3.2 mm，此时S密封密封性能和结构强度最优。根据此尺寸，通过有限元分析发现，等效应力与接触应力与软件预测结果相差不大，说明软件预测结果准确度高。将S密封最优结构尺寸及其结果与初始结构进行对比，密封圈外接触应力增加了11.79%，内侧接触应力增加了9.88%，最大等效应力下降了1.42%。虽然最大等效应力降低较小，但内、外侧接触应力提升很大。优化后S密封的密封性能和结构可靠性均优于初始结构下的S密封。

3.4 试验验证

经过上述优化后的S密封实物图如图10所示。将S密封安装至悬挂器上，放入模拟采油树中，模拟实际生产工况进行静压试验测试。试验压力采用1.5倍额定压力，试验现场图及数据如图11所示。试验数据表明，按照相关标准在1.5倍额定设计压力103.5 MPa(15 000 psi)下保压15 min，最终压降为0.77 MPa(112 psi)，下降率0.73%，符合密封标准，S密封满足密封性能要求。

图10 S密封实物图Fig.10 Photo of the S-seal

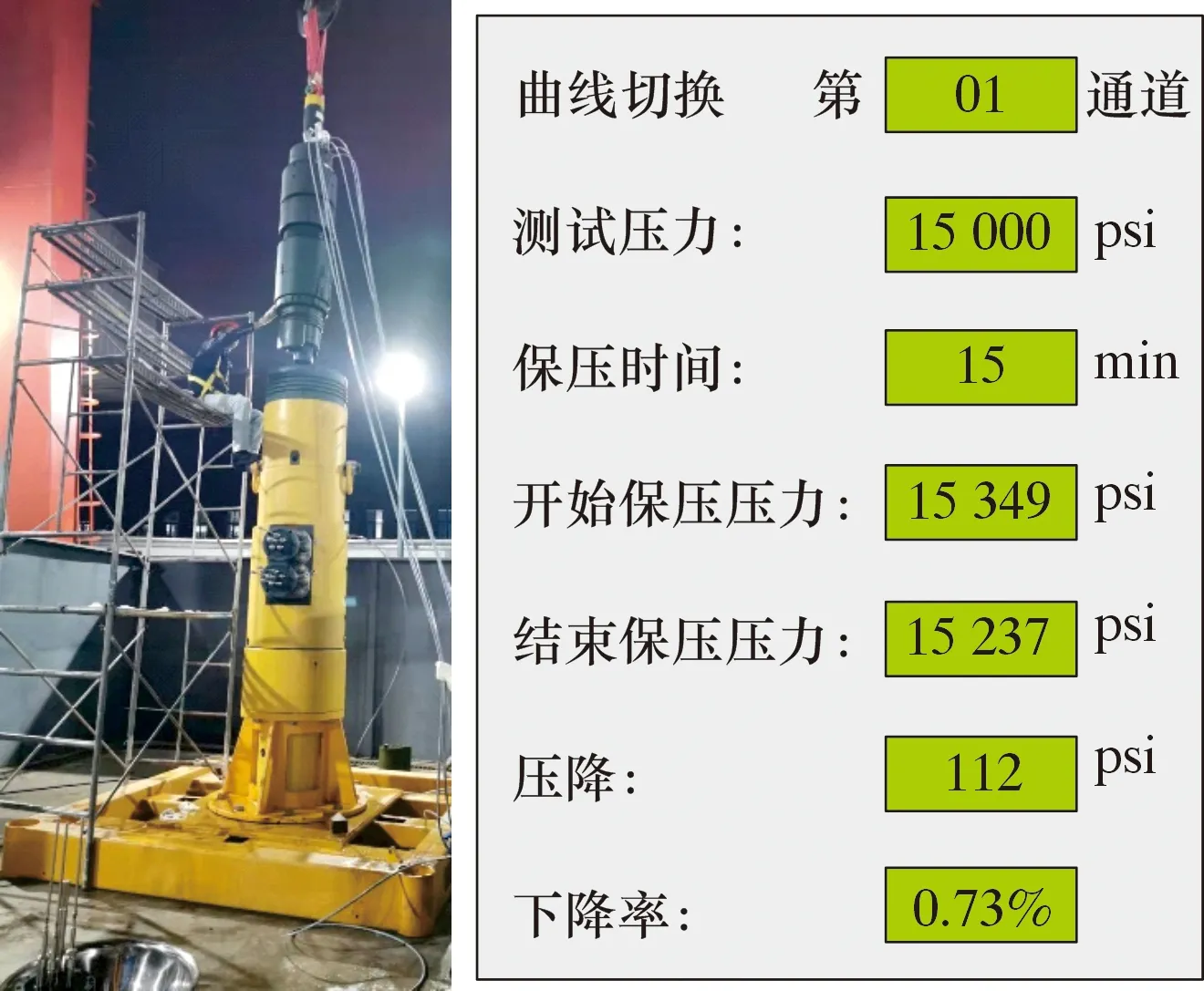
图11 试验现场及数据Fig.11 Testing site photo and data

4 结 论

(1)通过对S密封截面长度、截面宽度、弹簧直径及圆弧半径对结构强度与密封性能的影响规律研究发现：密封截面高度与弹簧直径对等效应力的影响均呈先减小后增大变化；截面宽度与等效应力负相关；圆环半径与等效应力呈正相关；密封截面高度、宽度与接触应力呈负相关；弹簧直径与内侧接触应力呈负相关，与外侧接触应力呈正相关；圆弧半径与内侧接触应力呈正相关，与外侧接触应力呈负相关。这说明在满足S密封等效应力的情况下，适当减小密封圈截面高度与宽度，增大圆弧半径有利于提高密封圈密封性能。

(2)将响应面优化前、后的S密封结构尺寸进行对比，外侧接触应力增加了11.79%，内侧接触应力增加了9.88%，最大等效应力下降了1.42%，优化后S密封在安全性和性能方面均优于初始结构下的S密封。

(3)所设计的S密封通过静压试验研究，在1.5倍额定设计压力下，满足密封性能要求。