拉伸作用下复合材料柔性管失效预测*

张元盛 刘涛 龙岩 王阳阳

(1.南方海洋科学与工程广东省实验室(珠海) 2.中国石油集团海洋工程(青岛)有限公司 3.中国石油大学(华东)石油工程学院)

0 引 言

纤维增强热塑性柔性管凭借其质量轻、比强度高、柔度大及耐腐蚀等优势，已逐渐成为深海油气开采管道主要替代品，随着油气开采逐渐走向深海，该类型管道的应用前景变得更为广阔[1-4]。

随着复合材料柔性管应用逐渐增多，其在不同载荷工况下的力学性能成为国内外专家学者研究的重点。C.S.CHOUCHAOUI等[5-6]求解了不同载荷工况下复合材料管的应力分布，并探讨了缠绕角及径厚比对应力分布的影响机理。XIA M.等[7-10]采用各向异性弹性理论，分析了内压载荷工况下复合材料柔性管的本构关系，并引入了温度载荷和缠绕角度的变化。M.P.KRUIJER等[11]采用二维理论计算方法和试验相结合，对轴向压缩作用下复合管的力学性能进行了研究，由于忽略了材料的非线性，所以误差较大。BAI Y.等[12-14]采用有限元和试验相结合的方法，分别研究了柔性管在拉伸、弯曲等载荷工况下的应力分布，为深入探讨不同工况下柔性管的力学性能奠定了理论基础。R.RAFIEE等[15]通过对不同直径的玻璃纤维缠绕管进行大量试验分析，并与所建立的渐进失效模型进行对比，验证了所建立的渐进失效模型有效性，并分析了纤维体积分数和缠绕角度对其承压能力的影响。LI G.H.等[16]对不同载荷工况复合材料柔性管的力学行为开展试验研究。LOU M.等[17-18]通过绳结构理论和试验结合的方式研究了温度与拉伸载荷作用下柔性管损伤失效。邢静忠(XING.J.Z.)等[19-20]采用弹性力学理论讨论了复合材料柔性管在轴向载荷，以及内部和外部压力下的应力应变关系，并进行了多角度优化研究。

从前期研究来看，对复合材料柔性管力学性能的理论分析多将其简化为二维平面应力状态[21]进行求解，忽略了柔性管的层间应力作用，因此无法完整识别其损伤失效模式；同时由于忽略了材料非线性力学行为[22]，导致计算精度差[4]。笔者在考虑热塑性材料非线性行为的基础上，结合三维弹性力学理论，构建复合材料柔性管渐进损伤失效预测模型，探究拉伸载荷工况下复合材料柔性管损伤失效机理。计算结果通过拉伸试验验证，并在此基础上开展参数敏感性分析。

1 理论模型

1.1 模型概况

本文以深水油气输送用复合材料柔性管为研究对象，其内外衬层及增强层基体均采用高密度聚乙烯(high-density polyethylene，HDPE)，增强体采用玻璃纤维。增强层以±55°角交替缠绕在内衬层上，并采用热熔方式粘结在一起。考虑到增强层以一定的缠绕角缠绕，材料坐标系与整体柱坐标系并不吻合，因此需要进行坐标转化。为准确模拟柔性管的三维本构关系，本文假定柔性管无初始损伤且各层粘结良好，建立的2个坐标系如图1所示。

图1 柔性管坐标系示意图Fig.1 Schematic diagram of the flexible pipe coordinate system

在图1中，φ为缠绕角，u(r)、v(r,z)、w(z)为其在柱坐标系下3个方向上的位移分量[18]。

本文所用的HDPE基体材料非线性力学行为由供应商在实验室测得，如图2所示。计算过程为采用切线模量法计算各阶段弹性模量，用于迭代计算。

图2 HDPE应力-应变曲线Fig.2 Stress vs.strain for the HDPE

1.2 理论模型求解

对拉伸载荷而言，柱坐标系下的柔性管应变几何方程可以简化为：

(1)

式中：εr、εθ、εz、γθr、γθz和γzr代表应变分量，1；u、v、w分别为各向位移分量，m；r、z分别为径向与轴向坐标分量，m。

各层平衡方程可写为：

(2)

式中：σr、σθ、τrθ、τzr分别为各向应力分量，MPa；上标i代表材料所在层数。

柔性管增强层各向异性铺层的正轴应力-应变关系如下：

(3)

式中：[σ]为应力矩阵，MPa；[ε]为应变分量矩阵，1；E为拉伸模量，MPa；ν为泊松比；G为增强层剪切模量，MPa；[C]为各层材料刚度矩阵，MPa。

不同坐标系下应变转换关系式为：

(4)

根据应变能守恒有：

(5)

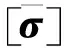
根据平衡方程和应变几何方程可以求得径向位移的一般表达式为：

(6)

当Si=1时(典型情况为各向同性材料)：

(7)

当Si=2时：

(8)

当Si≠1且Si≠2时：

(9)

式中：D1、D2为积分常数。

假定相邻层交界面处的径向应力和径向位移都连续，可以得到：

(10)

轴向平衡方程：

(11)

式中：TZ为拉伸载荷，kN；qa为内压力，MPa；r0为管道内径，m。

根据式(9)与式(10)并结合连续条件与扭矩平衡方程，可对柔性管进行应力应变求解。

[K][δ]=[q]

(12)

式中：[K]为整体管道刚度矩阵，MPa；[δ]为位移参数，m；[q]为载荷矩阵，N。

为准确预测柔性管渐进损伤失效，本文采用失效准则如下：

(13)

(14)

(15)

(16)

(17)

(18)

(19)

式中：σ1、σ2、σ3、τ12、τ13及τ23为材料坐标系下各向应力分量，MPa；Xt、Xc、Yt、Yc、Zt、Zc、X12、X13以及X23为玻纤带强度参数，MPa；Rft、Rfc、Rmt、Rmc、Rs、Rtd、Rcd分别为纤维拉伸失效、纤维压缩失效、基体拉伸失效、基体压缩失效、纤维基体剪切失效、拉伸分层失效及压缩分层失效系数，大于1则出现损伤，1。

采用的刚度衰减系数见表1。通过失效准则判断增强层发生失效，达到失效条件后通过表1的刚度衰减系数计算失效后的各向弹性常数。损伤发生之后弹性常数的非线性衰减速度通过退化因子控制。退化因子表达式如下：

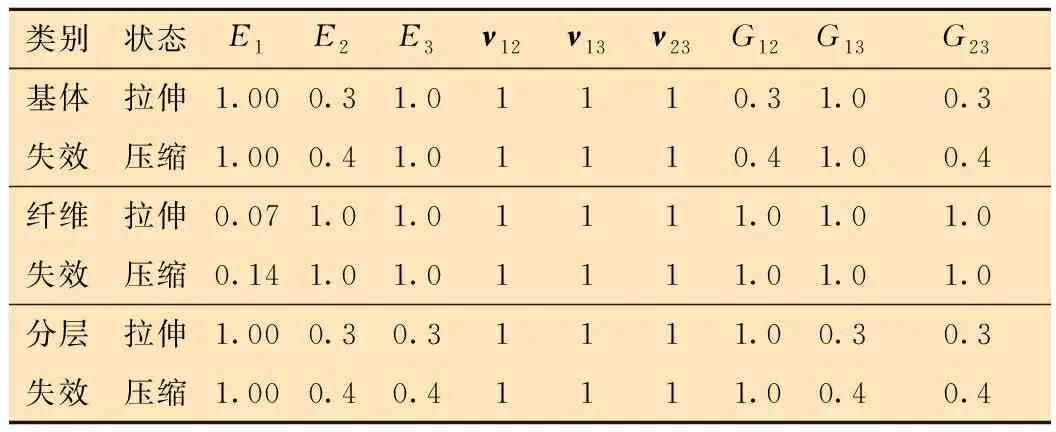
表1 复合材料刚度衰减系数[18]Table 1 Stiffness degradation coefficients of composite materials

i=ft,fc,mt,mc,s,td,cd)

(20)

式中：di为退化因子，1。

1.3 模型求解

采用计算软件Matlab编制代码实现柔性管在拉伸工况下损伤失效预测[23]。采用应力逐次迭代的方式进行加载，模型计算过程如图3所示，其中流程图展示了迭代和矩阵计算的详细过程。

图3 理论模型计算流程图Fig.3 Calculation workflow of the theoretical model

2 试验研究与验证

开展拉伸载荷作用下复合材料柔性管拉伸性能试验，并将理论模型计算结果和试验结果进行对比分析。

2.1 模型参数

本文柔性管内衬层和外保护层所用材料为HDPE，增强层由玻纤带以55°缠绕角正负交替缠绕而成。表2与表3分别为该柔性管的几何参数与材料参数。

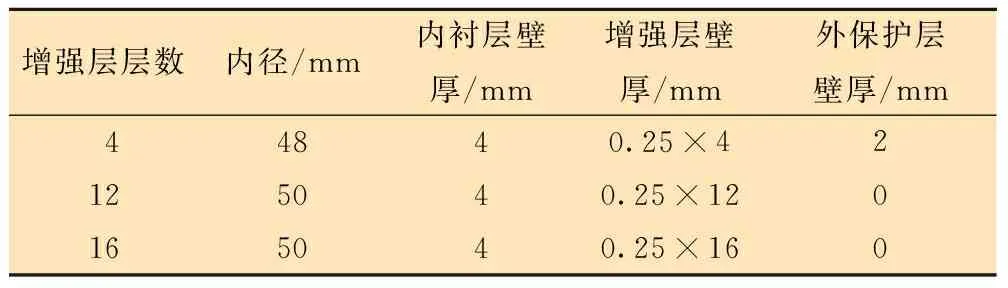
表2 柔性管几何参数Table 2 Geometric parameters of flexible pipes

表3 柔性管材料参数Table 3 Material parameters of flexible pipes

2.2 拉伸试验

开展充压工况下的柔性管拉伸性能试验，与理论模型计算结果进行对比，验证其合理性。试验样管(见图4)材料参数与结构尺寸如表2与表3所示。试验采用拉伸疲劳试验机，样管在开始拉伸之前施加2 MPa内压，加载方式为10 mm/min恒速加载。记录试验过程中的载荷位移曲线，并计算样管拉伸刚度进行结果对比。

图4 试验样管Fig.4 Pipe samples for experiments

图5给出了试验过程中样管结构损伤图。试验仅测量10%以内应变的载荷位移曲线，鉴于4层样管未曾剥离外包覆层，难以观察增强层破坏，12层与16层样管可明显看到增强层的损伤。随着拉伸载荷逐渐增加，样管出现了基体损伤(白化现象)，后期出现了样管渗水并伴有纤维断裂声。

图5 样管结构损伤Fig.5 Structural damage of pipes

2.3 试验验证

根据表2与表3的数据采用理论模型进行求解，将计算结果与试验进行对比，对比结果如表4与图6所示。

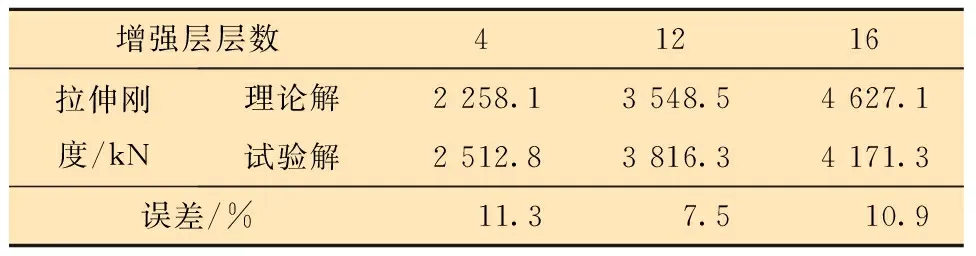
表4 理论模型计算结果与试验结果对比Table 4 Comparison between theoretical calculation and experimental results

图6 理论模型计算结果与试验结果对比图Fig.6 Comparison between theoretical calculation and experimental results

根据图6与表4对比结果可知，拉伸刚度误差在10%左右，鉴于不可避免的试验误差，可认为理论计算结果与试验结果符合度较好，误差在可接受范围之内，表明了理论模型的合理性。

首先定义与内衬层接触的增强层为最内层增强层，与外保护层接触的增强层为最外层增强层。基于此结论，进一步计算了柔性管不同损伤失效模式下的拉伸载荷，计算结果如表5所示。

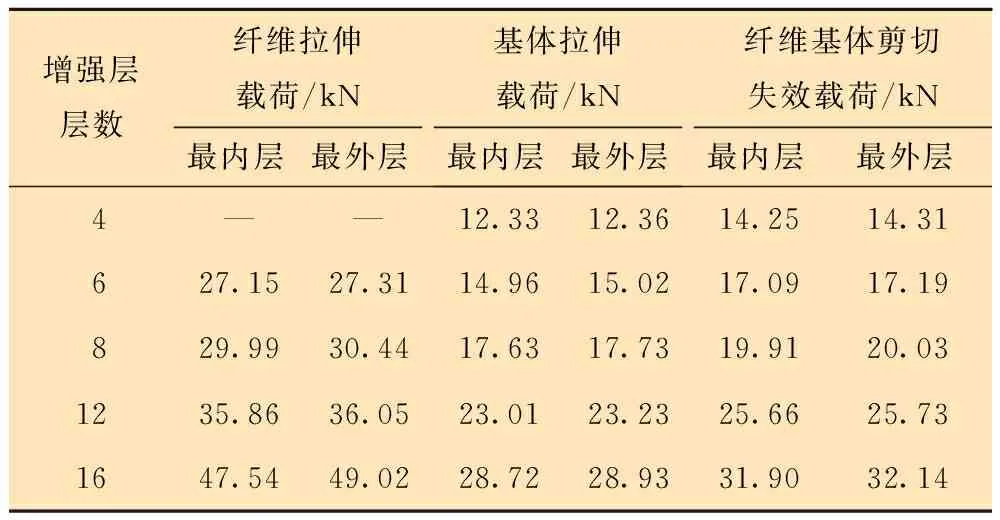
表5 理论模型拉伸失效计算结果Table 5 Predicted failure modes via the theoretical model

根据表5拉伸失效计算结果，复合材料柔性管增强层损伤失效模式主要包括纤维基体剪切失效、基体拉伸失效及纤维拉伸失效。基体拉伸失效为初始失效模式，而纤维拉伸断裂为最终失效模式。以4层样管失效载荷为例，首层失效拉伸载荷为12.33 kN，最终拉伸断裂失效载荷为27.15 kN，存在明显差异。

3 结果与讨论

在本文理论模型的基础上，研究缠绕角与径厚比对柔性管拉伸工况下损伤失效的影响。由于增强层为主要承载结构[18]，柔性管增强层缠绕角度对柔性管的力学性能有直接的影响。因此对失效的分析更多的关注增强层。

3.1 缠绕角度敏感性分析

为分析缠绕角对失效载荷的影响，首先计算了不同缠绕角度下柔性管的应力分布。以4层柔性管为研究对象，选取±15°～±85°之间的8个缠绕角度，计算结果如图7所示。

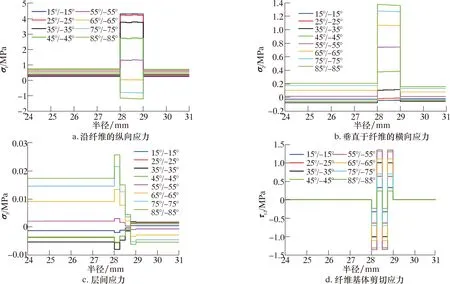
图7 局部坐标系下应力分布Fig.7 Stress distribution displayed in the local coordinate system

由图7可知：缠绕角对柔性管在拉伸工况下的应力分布有显著影响；柔性管在受拉伸载荷时，以±55°为分界点，随着缠绕角逐渐增加，沿着纤维方向的纵向应力逐渐由拉应力变为压应力，应力值为先下降后增加的趋势；横向应力与缠绕角度呈现正相关关系，其随着缠绕角增加逐渐由压应力变为拉应力，且整体呈现逐渐增加的趋势；层间应力同样以±55°为分界点，由压应力转变为拉应力，且呈现逐渐增加的变化趋势；而剪切应力则随着缠绕角度的增加先逐渐增加，当缠绕角超过±55°后，剪切应力逐渐减小。

通过进一步计算，对比了4层柔性管不同失效模式下的失效载荷随缠绕角度的变化情况。4层样管内径、内衬层厚度、外保护层厚度及玻纤带单层厚度与4层样管一致(见表2)，计算结果如表6所示。

表6 不同缠绕角度下柔性管失效拉伸载荷Table 6 Tensile failure load of flexible pipes with different winding angles

理论计算结果表明，增强层缠绕角度直接影响了柔性管在拉伸工况下的失效载荷和失效模式发生的顺序。

为了更加直观地分析缠绕角度对柔性管增强层首层失效与最终失效载荷的变化规律，将计算结果汇总，结果如图8所示。

图8 失效载荷曲线Fig.8 Failure load curves

由图8可以看出：当缠绕角度增大时，柔性管的首层失效载荷与最终失效载荷呈现先明显减小，后略有增加的趋势；缠绕角小于等于±55°时，增强层首先出现剪切失效，最终失效模式为纤维拉伸断裂；当缠绕角大于±55°时，增强层则首先出现基体拉伸失效，最终失效模式转变为剪切失效。根据图7的应力分析可知，当缠绕角较小时，纵向应力为控制载荷，而随着缠绕角度逐渐增大，横向应力转变为控制载荷。同时还可以看出，随着横向应力与层间应力由压应力逐渐转变为拉应力，基体失效模式也将由压缩失效转变为拉伸失效。根据应力分解可知，缠绕角度的变化改变了增强层各层在材料坐标系下的各向应力大小，进而直接影响柔性管结构内部的应力分布，而应力大小是损伤失效的直接原因。

3.2 径厚比敏感性分析

以12层柔性管为例，将柔性管厚度假定为不变值，通过改变内径，选取径厚比(内径与壁厚之比)范围为5～30、缠绕角为±55°的柔性管进行分析，详细分析了径厚比对柔性管失效载荷及失效模式的影响。计算结果如表7所示。

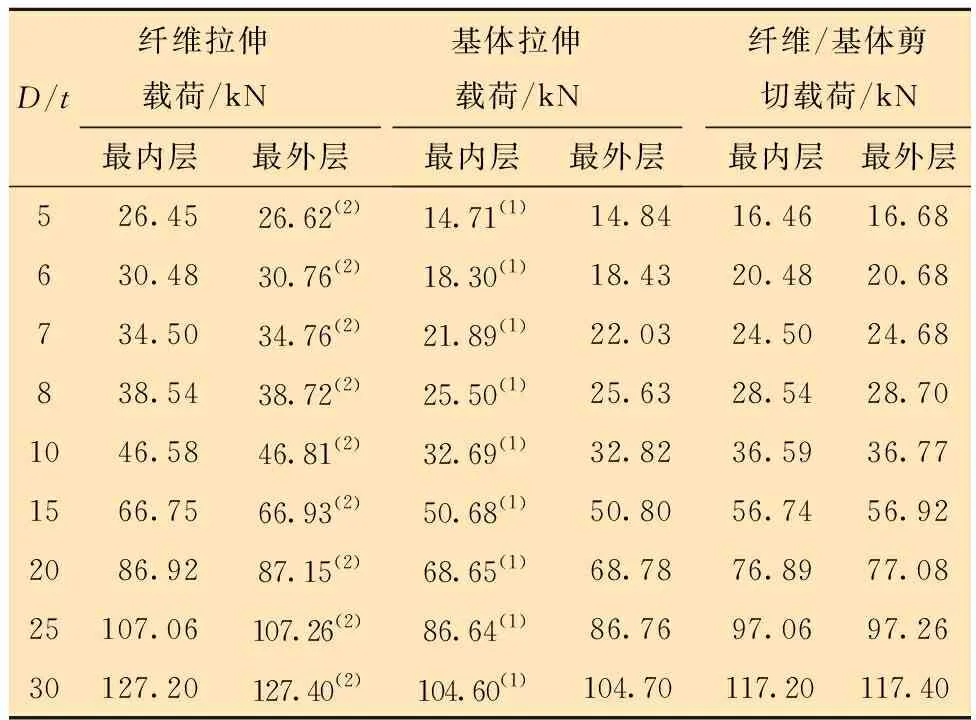
表7 不同径厚比条件下柔性管失效拉伸载荷Table 7 Tensile failure load of flexible pipes with different diameter-thickness ratios

根据表7的计算结果汇总，径厚比可以直接影响柔性管的承载能力。柔性管增强层的首层失效和最终失效载荷都随着径厚比的增加而增大，但径厚比并不影响失效模式的发生顺序；首层失效模式为基体拉伸破坏，而最终失效模式为纤维拉伸失效。由此可知，径厚比仅可影响柔性管整体应力分布大小，但无法控制载荷的变化，这主要由于随着管径增大改变了受力面积，进而改变了应力分布情况，提升了其承受拉伸载荷的能力。因此柔性管设计过程中需要关注径厚比的影响。

4 结 论

本文基于弹性力学理论，结合三维Hashin-Yeh失效准则与非线性刚度退化模型，考虑基体材料的非线性力学行为，建立了柔性管三维渐进失效模型。将理论模型计算结果通过试验进行了验证，证明了理论模型的准确性，在此基础上进行了参数敏感性分析，得到以下结论：

(1)柔性管增强层缠绕角度可以显著影响拉伸工况下柔性管应力分布，其各向应力变化趋势不同。当缠绕角较小时，纵向应力为控制载荷，而随着缠绕角度逐渐增大，横向应力转变为控制载荷。

(2)增强层缠绕角度直接影响了柔性管在拉伸工况下的失效载荷和失效模式发生的顺序。当缠绕角度增大时，柔性管增强层的首层失效载荷与最终失效载荷呈现先明显降低，后略有增加的趋势。小角度下增强层首层失效以剪切失效为主，最终失效为纤维拉伸断裂；当缠绕角度超过±55°时，首层失效为基体拉伸失效，最终失效模式转变为剪切失效。

(3)径厚比的增加将显著提升拉伸工况下柔性管的承载能力，但径厚比并不影响失效模式的发生顺序。首层失效模式为基体拉伸破坏，而最终失效模式为纤维拉伸失效。在柔性管设计过程中应关注径厚比的影响。