人行桥阻尼索减振研究

彭文林，禹见达,2，胡 磊，孙洪鑫,2

(1.湖南科技大学 土木工程学院，湖南 湘潭 411201；2. 湖南科技大学 结构抗风与振动控制湖南省重点实验室，湖南 湘潭 411201)

随着我国经济的不断发展，城市道路的车流量越来越大，为了进行人车分流，人行天桥的数量也越来越多。人行桥在城市立体交通网络中发挥了巨大作用，其跨度随着路面宽度的增加和高强材料技术的进步而不断增加，其固有频率也随之不断降低。大跨度人行桥的基频往往会降低到步行力的频率范围内，从而发生人致振动[1-2]，著名的案例有日本的T桥[3]、伦敦的千禧桥[4]、巴黎的Solférino桥等[5-6]。桥梁过大的振动会导致行人行走困难，严重时可能导致行人恐慌，甚至引发踩踏事故，过度的人行桥振动亟需解决。

现有桥梁振动控制措施主要有增加结构刚度的静力学措施和调谐减振的动力学措施两种，增加结构刚度是一种很直观的方法，但其花费的成本很高，目前主流方法还是调谐减振的动力学措施。调谐质量阻尼器(tuned mass damper, TMD)自Frahm提出、Den Hartog改进以来，在抑制人行桥的人致振动方面得到了深入研究。汪志昊等[7]使用刚度与阻尼参数分离的微型电涡流TMD对人行桥模型进行减振试验；罗晓群等[8]采用TMD对国内某单斜面索拱支承曲梁人行桥进行人致振动控制研究；Tubino等[9]对人行天桥在竖直方向的最优TMD设计进行了研究；李晓玮等[10]实测在相同人行荷载作用下安装TMD系统前后的人行桥振动响应，验证了TMD对人行桥的减振效果；肖新标等[11]研究了移动荷载作用下的桥梁进行TMD振动控制效果。TMD在人行桥人致振动控制方面得到了广泛应用，如日本T桥、日本芦屋人行天桥[12]、伦敦的千禧桥、巴黎的Solférino桥等、绵阳一号人行桥[13]都采用TMD进行减振。

人行桥在使用过程中，桥上行人与桥梁结构存在相互作用，行人自身将作为一个动态的质量-弹簧-阻尼(mass spring damper，MSD)系统参与桥梁振动[14-15]，这时耦合了行人的人行桥系统振动频率、阻尼等参数将会发生改变[16-18]，已经调谐好的TMD可能失调[19]。针对人行桥振动频率在一定范围内变动的特点，Klaus Lievens等[20]提出了一种考虑模态参数不确定的TMD鲁棒优化设计方法；霍林生等[21-22]研究表明多重调谐质量阻尼器(multiple tuned mass dampers,MTMD)具有更好的鲁棒性，采用MTMD比TMD更适合用于人行桥减振；Wang等[23]通过现场实测和数值模拟研究发现MTMD比TMD对钢结构人行天桥有更好的减振效果。

TMD减振频带窄的缺点，在轻钢人行桥减振方面变得特别突出。轻钢人行桥本身质量小，桥面人群质量可能超过结构本身[24]，在不同的人群密度下，人行桥的振动频率变化范围较大。为了保证调谐减振的效果，伦敦千禧桥除安装TMD进行减振外，还采用巨型刚臂、长连杆安装了黏滞阻尼器辅助减振；华旭刚等针对绵阳一号人行桥结构特点首先应用连杆提高了结构刚度，然后结合TMD进行了人行桥减振。

黏滞阻尼器等液压流体阻尼器具有巨大的耗能能力，且其减振效果受结构频率变化的影响小，但其必须利用阻尼器两端的相对运动才能耗能，目前未有应用液压流体阻尼器抑制桥梁弯曲大幅振动的报道。禹见达等[25]提出了一种复合阻尼索减振技术，以较小的成本极大地提高了阻尼器的支撑杆长度，并通过模型试验验证了复合阻尼索利用黏滞阻尼器抑制高耸结构的减振效果，遗憾的是其未进行深入的复合阻尼索减振理论分析。

以最常见的轻钢简支梁人行桥为研究对象，针对其竖弯第一阶模态的大幅振动，本文设计了一种自锚式阻尼索。首先建立了阻尼索-简支梁振动方程，获得了人行桥附加阻尼比解析计算公式，然后以理想黏性的电涡流阻尼器为耗能元件[26]，通过模型试验验证了阻尼比解析计算公式的正确性。为了分析人行桥频率大幅变化时阻尼索的减振效果是否会削弱，本文还设置了一组对照试验，试验结果表明结构频率大幅变化对阻尼索的减振效果影响小。最后开展了简支梁桥的阻尼索减振参数理论分析，获得了主梁附加阻尼比与阻尼索各参数的关系。

1 人行天桥-复合阻尼索系统

人行桥下方为车行道，因此在桥下空间安装阻尼索可能妨碍交通而很难被采纳，但人行桥上方较为空旷，为阻尼索安装提供了可利用空间。人行桥型式多种多样，为方便起见，本文仅以简支梁桥模拟人行桥研究阻尼索的减振效果。在桥梁跨度范围内适当位置安装两立柱(后期可以装饰为灯柱)，阻尼索张拉方法如图1所示，在两端距离支座x1处分别对称竖立两根高为H的立柱，在立柱顶点与支座间张拉阻尼索，阻尼索由阻尼器、复位弹簧并联后再与主索串联而成，复位弹簧预先张拉，并保证弹簧弹性力远大于阻尼器阻尼力，这样就能使阻尼索时刻处于拉紧状态；在张拉阻尼索的同时在两根立柱之间连接抗拉索，抗拉索需要能够能提供较大的弦向刚度。当主梁发生第一阶竖弯振动时，两根阻尼索拉力的水平分量可以互相平衡，竖向分量通过立柱传递作用于主梁，由其中的阻尼器阻尼力消耗主梁动能。

图1 人行桥-阻尼索结构示意图Fig.1 Structure diagram of footbridge with damping cable

对于主梁的第一阶弯曲模态振动，根据对称性取桥梁-阻尼索系统左半边进行分析，如图2所示，设主梁的抗弯刚度为EI，长度为L，质量线密度为ρ，主梁挠曲线为u(x,t)，则主梁竖弯振动方程为

(1)

式中:f(x,t)为人行桥所受桥面分布荷载；Fp为阻尼索动张力；δ(x-x1)为δ函数。

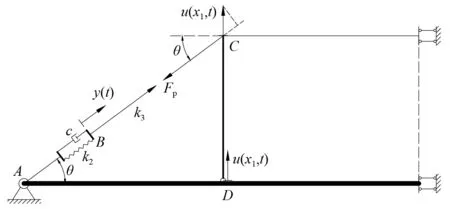
图2 简支梁-阻尼索力学模型Fig.2 Mechanical model of simply supported beam with damping cable

阻尼索由主索、阻尼器和复位弹簧组成而成，力学参数包括：主索刚度k3、阻尼器阻尼黏性系数c和复位弹簧刚度k2。当主梁发生第一阶模态竖弯微幅振动时，忽略立柱、抗拉索及AB段主索的轴向变形，同时考虑复位弹簧、阻尼器和BC段主索变形，则阻尼索动张力为

(2)

根据模态分析法，主梁振动可表示为振型函数φ(x)=sin(πx/L)与时间函数z(t)的乘积：u(x,t)=φ(x)·z(t)，将其代入式(1)，在方程两边同乘以振型φ(x)并积分得到

(3)

由式(2)、式(3)联立可得到主梁-阻尼索振动方程

(4)

式中，η=2φ(x1)2sin2θ为阻尼索影响系数。

2 人行桥-阻尼索系统自由振动解析解

As3+Bs2+Cs+D=0

(5)

式中：A=cm1；B=(k2+k3)m1；C=(ck1+ck3η)；D=[(k2+k3)k1+k2·k3η]。

对于式(5)的解，可由三次方程求根公式求解, 设α=B2-3AC,β=BC-9AD,γ=C2-3BD。当Δ=β2-4αγ>0时，式(5)的三个根s1，s2和s3分别为

(6)

z(t)=X1es1t+eRe(s2)t(X2eIm(s2)it+X3e-Im(s2)it)

(7)

式中，X1,X2,X3由初始条件确定，其中第一项为实数解，在主梁振动过程中迅速衰减，因此主梁自由振动的特性主要由后面两项所决定，系统振动的圆频率

(8)

主梁自由衰减振动附加阻尼比为

(9)

由结构动力学知识可知，结构附加阻尼比越大，则结构自由振动的衰减速度越快，相同外加激励作用下结构的振幅越小，因此，附加阻尼比可以直观描述阻尼索对主梁的减振效果。

3 模型试验验证

3.1 试验模型

为了验证附加阻尼比解析解式(9)的正确性，本文采用简支钢梁模拟人行桥，采用增加配重方式模拟行人对桥梁固有频率的影响，在人行桥两端对称安装阻尼索进行减振试验，试验模型左半部分如图3所示，实际模型图如图4所示。简支钢梁采用两根相同的槽钢并排布置，每端立柱采用两根直径12 mm的螺杆，与槽钢之间采用夹具连接，立柱与阻尼器距离为x1。

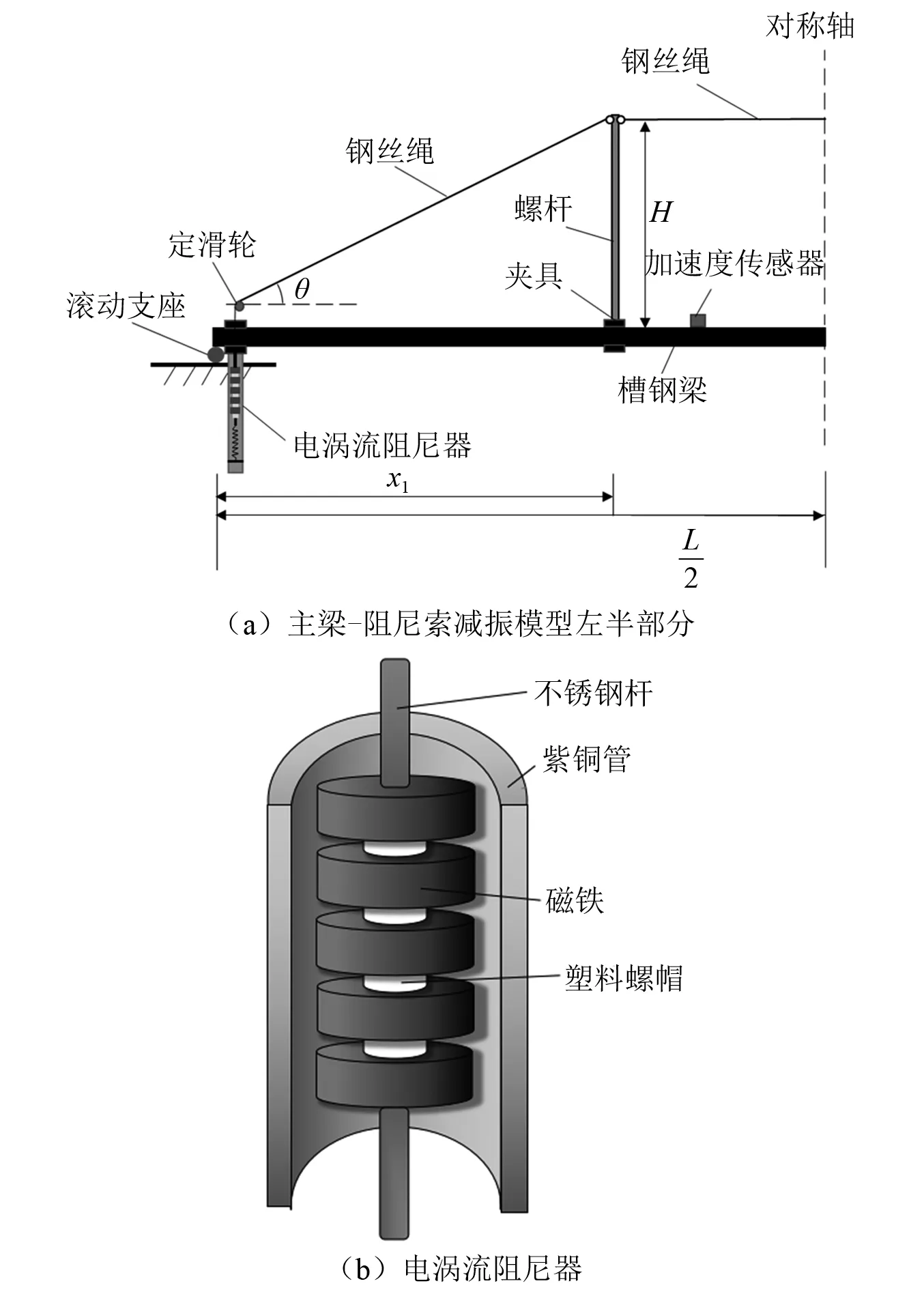
图3 试验装置原理图Fig.3 Schematic diagram of experimental device

图4 试验现场照片Fig.4 Experimental site photo

阻尼索包含主索、复位弹簧和管式电涡流阻尼器，主索为直径1 mm的钢丝绳；电涡流阻尼器由铜管、磁铁组成，如图3所示，铜管通过夹具固定在主梁支座处，磁铁由下端复位弹簧和上端主索牵引与铜管发生相对运动从而产生电涡流阻尼力。试验模型的各物理参数如表1所示。

表1 试验模型参数Tab.1 Parameters of experimental model

电涡流阻尼器低速运动时是一种理想的黏性阻尼器，试验采用铁铷硼高强磁铁，每片磁铁外径48 mm、内径10 mm、厚度20 mm，磁铁采用同极相斥方式逐级增加，磁铁间采用15 mm厚塑料螺母分隔；紫铜管内径55 mm、外径65 mm。阻尼器磁铁数量与电涡流阻尼器的黏性阻尼系数关系经试验测得如表2所示。

表2 电涡流阻尼器阻尼系数Tab.2 Damping constant of eddy current damper

3.2 主梁附加阻尼比的试验值与理论值对比

对主梁施加人工共振激励，当主梁振幅达到设定值时撤除激励，主梁随后进入自由振动状态，采集主梁振动加速度，得到其加速度振动衰减曲线。由加速度数据进行数值拟合得到衰减包络线，从而获得不同阻尼索参数下的主梁阻尼比ζE。

在阻尼索未安装时，主梁振动加速度时程曲线如图5(a)所示，然后在结构上安装阻尼索，改变电涡流阻尼器中的磁铁数量，获得主梁加速度时程。典型加速度时程曲线如图5所示，图5(b)为不加装磁铁，即阻尼器黏性系数为0时的加速度时程，此时拉索预张力作用于定滑轮上，定滑轮摩擦力可以消耗结构振动的部分能量，图5(c)、图5(d)分别为阻尼索安装2级、5级磁铁电涡流阻尼器时主梁振动的加速度时程，由图5可以看出，随着阻尼索阻尼器磁铁数量的增加，即黏性系数的增大，结构自由振动衰减越来越快，表明阻尼索能够快速地消耗结构振动的能量。

图5 主梁振动加速度典型时程Fig.5 Typical acceleration time history of main girder

对加速度衰减段采用最小二乘法拟合，为避免振幅对阻尼比分析结果的影响，除无阻尼索的裸梁自由振动外，计算阻尼比时选取加速度峰值从2.0 m/s2衰减至0.5 m/s2左右区间进行拟合，如图5所示。由拟合结果获得：主梁结构(裸梁)本身阻尼比为0.12%；阻尼索阻尼器黏性系数为0时主梁阻尼比为0.48%，说明滑轮轴承内滚珠受内、外钢圈预压力产生的摩擦力可以消耗主梁振动动能。

(10)

表3 附加阻尼比试验值和理论值Tab.3 Experimental value and theoretical value of additional damping ratio

图6 附加阻尼比试验值和理论值对比Fig.6 Comparison of experimental value and theoretical value of additional damping ratio

阻尼索为主梁提供的附加阻尼比与阻尼器黏性系数的关系，如图6所示。由图6可知：①当电涡流阻尼器的阻尼系数从0增加到145 N·s/m时，主梁模型试验实测阻尼比由0.48%增加到4.28%，由阻尼器黏性阻尼力产生的附加阻尼比由0增大到3.80%，由式(9)计算得到的附加阻尼比理论值从0增大到3.75%，理论值与实测值吻合；②随着阻尼器黏性系数的增大，主梁附加阻尼比近似线性增大。

3.3 主梁频率改变时附加阻尼比理论值与试验值对比

轻钢人行桥本身质量小，桥面人群质量可能超过结构本身，在不同的人群密度下，人行桥的振动频率变化范围较大，该状况对阻尼索减振效果的影响值得讨论。为此，在主梁跨中增加一个10 kg的砝码作为配重，主梁竖弯频率由2.42 Hz(模型一)变为2.01 Hz(模型二)，同样通过主梁衰减振动加速度时程曲线拟合得到主梁附加阻尼比理论值和试验值如表4所示。

表4 模型二附加阻尼比试验值和理论值Tab.4 Experimental value and theoretical value of additional damping ratio of modeII

对比表3、表4可知：与主梁未增加配重相比，增加配重后阻尼索为主梁提供的附加阻尼比有所降低，这是因为系统质量增加，振动能量增加，而相同振幅条件下阻尼器单周耗能不变，导致阻尼器单周耗能与系统总动能比值降低。

主梁增加配重后阻尼索提供的主梁附加阻尼比与阻尼器黏性系数的关系如图7所示，同样可看出，试验测得的主梁附加阻尼比与理论解吻合，并随着阻尼器黏性系数的增大而近似线性增大。

图7 模型二主梁附加阻尼比试验值与理论值对比Fig.7 Comparison of experimental value and theoretical value of additional damping ratio of mode II

由图6、图7可知：①结构阻尼索减振附加阻尼比计算式(9)与模型试验结果吻合良好，验证了附加阻尼比理论计算结果的准确性；②通过增加配重模拟人行桥固有频率改变时，阻尼索同样可以为主梁提供较大的附加阻尼比；③阻尼索为主梁提供的附加阻尼比随阻尼器黏性系数的增大而近似线性增大，并且受主梁固有频率变化的影响小，通过增大阻尼器黏性系数可以方便地获得理想的减振效果。

4 阻尼索减振效果参数分析

上述试验已验证了阻尼索为不同质量主梁提供的附加阻尼比解析解的准确性，为了更好地了解阻尼索对桥梁的减振性能，需要对阻尼索减振进行参数分析。影响阻尼索附加阻尼比ζa的主要参数包括阻尼索材料参数：主索刚度k3、复位弹簧刚度k2、阻尼器黏性系数c，阻尼索几何参数：立柱安装位置x1与高度H。为探究各参数对阻尼索附加阻尼比的影响，以未加配重的试验梁为研究对象，分析阻尼索附加阻尼比ζa与各参数的关系。

4.1 主索刚度与复位弹簧刚度对减振效果的影响

当立柱安装位置x1=0.25L,H=0.15L，复位弹簧刚度k2=0.2k1，不同阻尼器黏性系数下的主索刚度k3与附加阻尼比的关系，如图8所示。

由图8可以看出：当阻尼索其他参数一定时，阻尼索对结构附加阻尼比随着主索刚度k3与复位弹簧刚度k2之比的增大而增大，但当刚度比大于10以后，继续提高主索刚度k3对提高阻尼索减振效果不明显，此时，增大阻尼器黏性系数对提高阻尼索减振效果明显。

图8 附加阻尼比与刚度比k3/k2的关系Fig.8 The relationship between additional damping ratio andstiffness ratio k3/k2

4.2 阻尼器阻尼系数对减振效果的影响

确定阻尼索的安装位置x1=0.25L,H=0.15L和拉索弹簧的刚度k2=0.06k1,k3=3k1，改变阻尼索的阻尼黏性系数，由式(9)计算得到阻尼器阻尼黏性系数c与附加阻尼比ζa的关系，如图9所示。

图9 附加阻尼比与阻尼系数c的关系Fig.9 The relationship between additional damping ratio and damping constant c

由图9可以看出，在阻尼器黏性系数较小的情况下，结构附加阻尼比与阻尼器黏性系数的增大而增大，二者近似成正比。但当阻尼器黏性系数超过最优值时，结构附加阻尼比随阻尼器黏性系数的增大而减小，其间存在一最优阻尼器黏性系数。

4.3 立柱高度及安装位置对阻尼索减振效果的影响

当复位弹簧刚度k2=0.08k1,主索刚度k3=3k1，阻尼器黏性系数c=100 N·s/m，不同立柱高度和安装位置的主梁附加阻尼比如图10所示。

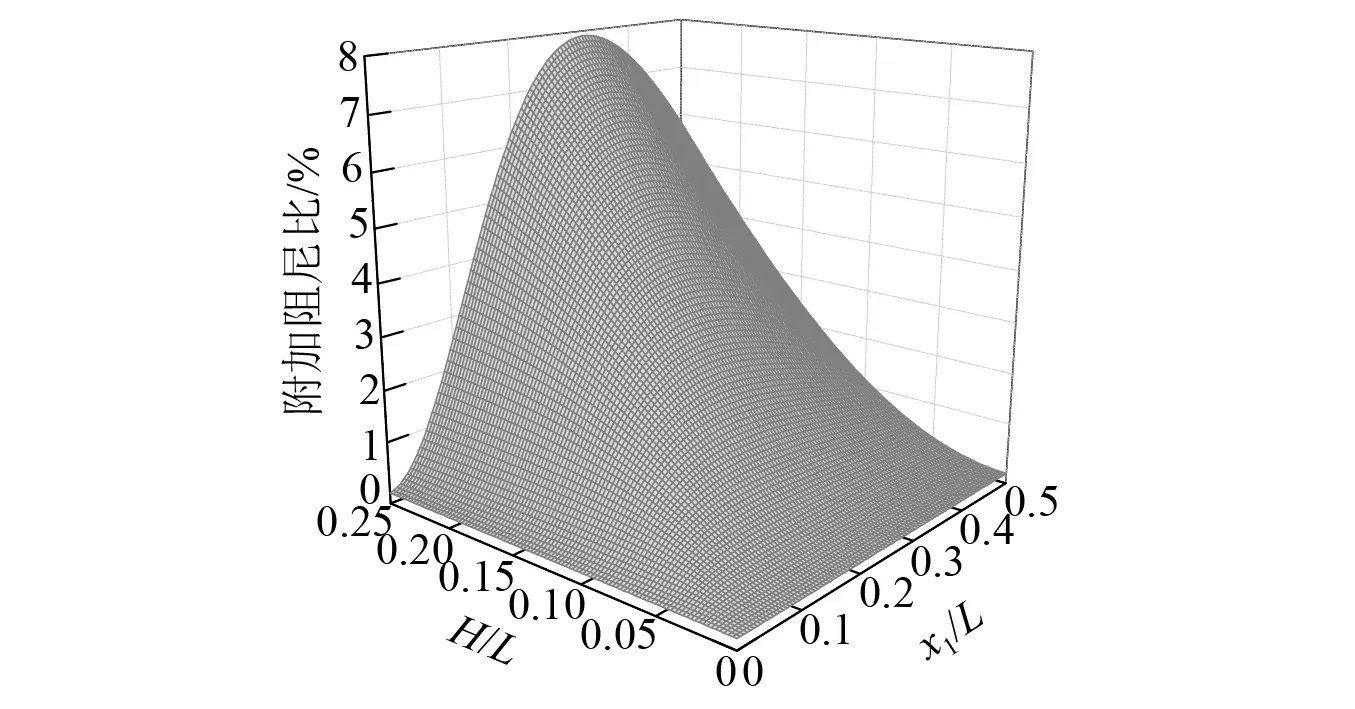
图10 附加阻尼比与安装位置的关系Fig.10 The relationship between additional damping ratio and installation position

由图10可知：①立柱高度H越大，阻尼索对主梁的减振效果越好；②选定立柱高度后，阻尼索对主梁的减振效果随立柱安装位置x1的增大先增大后减小，x1存在一个与立柱高度有关的一个最优安装位置。

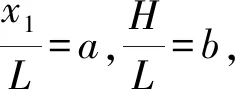
(11)

求解式(11)可得到立柱最优安装位置，即在相同的阻尼索材料参数和立柱高度条件下获得主梁最大的附加阻尼比。

5 结 论

本文采用阻尼索抑制人行桥第一阶竖弯振动，首先建立了人行桥-阻尼索结构的三阶微分方程，获得了人行桥的自由衰减振动附加阻尼比解析解，随后通过模型试验验证了该解析解的正确性；并对阻尼索减振性能进行了参数影响分析，得到了如下结论：

(1)采用阻尼索可以有效地抑制人行桥第一阶模态竖弯振动，增加主梁附加质量改变主梁频率时，基本上不影响阻尼索的减振效果。

(2)在阻尼索阻尼器黏性系数较小的情况下，主梁附加阻尼比与阻尼系数呈正比，但随着黏性系数的增大，主梁附加阻尼比达到最大值后出现下降趋势。

(3)主索刚度k3与复位弹簧刚度k2之比较小时，主梁附加阻尼比随刚度比的增大而近似成正比增大；当刚度比较大时，主梁附加阻尼比随刚度比的增大仅稍有增大，此时，主梁附加阻尼比随阻尼器黏性系数的增大而近似成正比增大。

(4)随立柱安装位置x1的增加，即立柱由两端向跨中移动过程中，主梁附加阻尼比先增大、后减小，因此，存在最优立柱安装位置。