水产品中铜含量的不确定度评估

赵全东，高 娜，李天爽，郎宇奎，李冠颖，李改娟

（吉林省水产科学研究院，吉林长春 130033）

本实验依据《化学分析中不确定度的评估指南》（CNAS—GL006：2019）[1]和《测量不确定度评定与表示》（JJF 1059.1—2012）[2]，参照食品安全国家标准食品中铜的测定[3]，对原子吸收法测定鱼肉中铜含量的不确定度进行分析，为实验室内部质量控制提供数据支持，保障实验数据准确性、可靠性。

1 材料与方法

1.1 试剂与仪器

标准品：铜（1 000 μg·mL-1），国家有色金属及电子材料分析测试中心；硝酸（优级纯，国药集团化学试剂有限公司）；实验室用水为超纯水一级水。

原子吸收分光光度计，岛津AA-6800；微波萃取仪，MARSX PRESS美国CEM公司。

1.2 试验方法

1.2.1 样品制备

称量：称取粉碎均匀的鱼肉样品1.000 g，精确到0.001 g；消解：在已称好的样品中，先后加入双氧水1 mL、硝酸3 mL，浸泡30 min，用微波消解仪消解[4]，经微波消解冷却后取出消解罐，在电热板上于140～160 ℃赶酸至1 mL左右，消解罐放冷后，将消化液转移至25 mL容量瓶中，用少量水洗涤消解罐2～3次，合并洗涤液于容量瓶中，用水定容至刻度，混匀备用，同时做试剂空白试验[5]；测定：使用原子吸收分光光度计测试样品上机测定液和试剂空白样液得到其吸光值[6]。

1.2.2 不确定度来源分析

通过对测量过程、计算方式等进行综合分析，其不确定度来源主要有以下几个方面：天平称量、标准溶液、溶液配制过程中容量瓶、移液器、标准曲线拟合、回收率、仪器测量重复性等因素引起的不确定度。

1.2.3 数学模型建立

数学模型的建立见式（1）。

式中：X为试样中的铜含量，mg·kg-1；c为测试样品溶液中铜含量，μg·mL-1；V为试样处理后的总体积，mL；m为试样质量，g。

2 结果与分析

2.1 天平称量鱼肉引入的不确定度

天平的称量结果：m=1.000 g，精确到0.001 g。JJG 539—1997规定，该准确级的天平在该称量范围内最大允差是±0.000 5 g[7]。最大允许误差包括了天平校准、称量变动性引起的最大允许误差（若天平显示的数值不是自动显示而是人员读数所得，则最大允差还包括人员读数引起的最大误差），按均匀分布，则不确定度为，由于天平称量两次（空瓶和空瓶加样品），天平引起的标准不确定度为=0.000 410 g，则天平称量引起的相对标准不确定度为

2.2 标准溶液引入的不确定度

铜元素标准溶液证书质量浓度是 （1 000±7）μg·mL-1，（k=2），则铜元素标准溶液引入的标准不确定度相对标准不确定度为

2.3 溶液配制过程容量瓶引入的不确定度

2.3.1 25 mL单标线容量瓶引入的不确定度

（1）容量允差带来的不确定度。根据《常用玻璃量器检定规程》（JJG 196—2006）规定，20 ℃时 25 mL容量瓶A级的容量允差是±0.03 mL。取矩形分布，则其不确定度

（2）温度带来的不确定度。假设按正态分布P=0.95，c=1.96，则由此引起的不确定度分量为

2.3.2 100 mL单标线容量瓶体积引入的不确定度

（1）容量允差带来的不确定度。根据《常用玻璃量器检定规程》（JJG 196—2006）规定，20 ℃时 100 mL容量瓶A级的容量允差是±0.10 mL。取矩形分布，则其不确定度

（2）温度带来的不确定度。假设按正态分布P=0.95，c=1.96，则由此引起的不确定度分量为

则容量瓶引入的相对标准不确定度为

2.4 移液器引入的不确定度

需移液管量取的体积为v=1 000 μL，根据《移液器检定规程》（JJG 646—2006）规定1 000 μL可调移液器容量允差为±1.0%。容量允差包括体积校准、充满液体至滴定刻度的变动性（即重复性），人员读数，取矩形分布，则，则可调移液器引入的相对标准不确定度为

2.5 标准曲线拟合引入的不确定度

浓度和测量值的关系如表1所示。得到的拟合校准曲线y=bc+a，a为拟合曲线的截距，a=11.156；b为拟合曲线的斜率，b=37 396.951，相关系数R=1.000 0。对样品测定6次，由方程求得平均浓度 为7.25 μg·L-1，折合为试样中铜含量X=181.25 μg·kg-1，则标准曲线拟合带来的不确定度按公式（2）计算[8]，残差Sy按公式（3）计算。

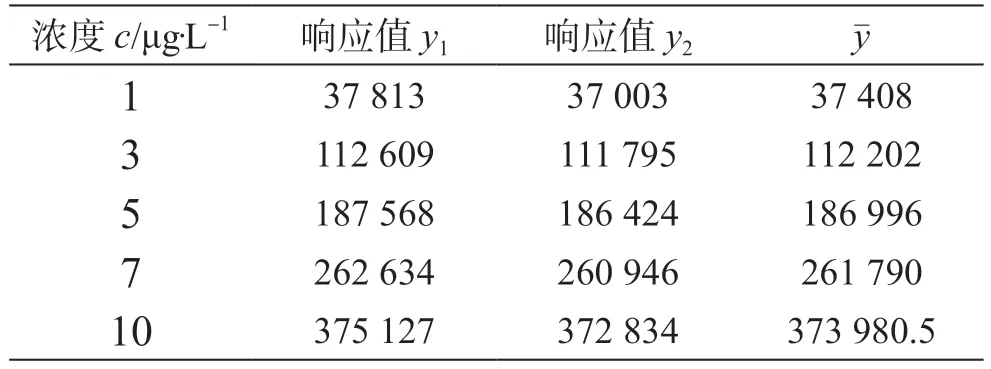
表1 标准曲线浓度与响应值关系

式中：Sy为回归曲线的剩余标准差（残差的标准差）；p为待测样品的重复测定次数，p=6；n为回归曲线的点数，n=10（每个标准溶液浓度进行2次测量共10次）；c_为待测样品浓度的平均值c_= 7.25 μg·L-1；c0为回归曲线各点浓度的平均值， 5.2 μg·L-1；b为拟合曲线的斜率，ci为标准溶液各点的浓度值，分别为1 μg·L-1、3 μg·L-1、5 μg·L-1、7 μg·L-1和10 μg·L-1。

计算得残差Sy=819.093 452，标准曲线拟合带来不确定度u(c)=0.012 2，标准曲线引入的相对不确定度为

2.6 回收率测定带来的不确定性分析

本实验测定6次，回收率分别为93.67%、90.50%、90.17%、89.00%、96.83%和90.67%，平均回收率Ravg=91.81%。假定回收率服从矩形分布，则样品回收率的标准不确定度为

对回收率检测结果进行显著性检测，如果平均回收率与100%有显著性差异，则平均回收率应作为测量结果的不确定度来源予以评估，否则不必进行回收率不确定度评估。现对本实验中回收率进行显著性检测，t值按式（4）计算。

计算所得t值与95%置信度下，n-1自由度的双边临界值tcrit相比较（其中n是用来评估平均回收率的测试结果的数目），t值计算结果为3.62，查表得95%置信度下，n-1=5自由度的双边临界值tcrit为2.57，t≥tcrit，则平均回收率与100%有显著性差异。本实验中平均回收率应作为不确定度来源之一进行评定，其相对标准不确定度为

2.7 仪器测量重复性的不确定度评定

设备信号均值的标准不确定度是由于仪器的重复性测定引起的，本试验重复6次测得数据分别为6.88 μg·L-1、7.43 μg·L-1、7.58 μg·L-1、7.26 μg·L-1、 7.42 μg·L-1和6.93 μg·L-1，测试次数n=6，c_=7.25 μg·L-1，试样中铜含量平均值X=181.25 μg·kg-1，结果的相对标准偏差为3.948%，仪器测量重复性引入的相对标准不确定度为

3 合成标准不确定度的评定

合成标准不确定度为

4 扩展不确定度的计算与结果

取k=2，被测量值大约95%含于此区间，则其相对扩展不确定度为U=k×ucrel=2×5.548= 11.10 μg·kg-1。本次试验测定样品中铜的含量最 佳 估 值 为181.25 μg·kg-1，则 其 结 果 可 表 示 为（181.25±11.10）μg·kg-1。

5 结论

不确定度是衡量实验数据质量高低的量化指标，分析不确定度对于提高实验质量具有指导意义。本文中回收率引入的相对标准不确定度分量（2.462%）占主要部分，来源于前处理方法及操作的稳定性；仪器测量重复性引入的相对标准不确定度为1.612%，与仪器的稳定性有关；移液器引入的相对标准不确定度0.577%是第三位；标准曲线线拟合引入的相对标准不确定度与仪器的性能（灵敏度、稳定性）以及定量点的测试次数和其均值在标线的位置有关；称量、容量瓶定容引入的不确定度分量占比较小。