“基本不等式”融入课程思政教学设计

蓝诗涵 宾红华 刘小辉

(福建省厦门集美大学理学院 361021)

1 问题提出

数学课程中“三全育人”目标的实现，需要课程思政的融入，与学科教学协同并进，培养学生的理性思维、科学精神、个性品质和数学核心素养.课程思政要想有效融入高中数学课堂，要求教师充分挖掘数学教学活动中的育人价值和思政元素，需将课程思政和学科德育两种课程理念清晰地区分开，并探究课程思政融入高中数学课堂的教学设计.

2 课程思政的内涵

课程思政是一种教育理念，数学课程需要承载思想政治教育所要承担的责任.课程思政从另一个角度思考，它是一种课程观，因此思想政治教育的融入要贯穿于数学课程教学的各个环节，从而促进学生的发展.

课程思政与学科德育是两种不同的概念,所以不能将课程思政与学科德育两种概念相混淆.高中数学课程融入课程思政需以学生发展为本,落实立德树人的根本任务,提升数学核心素养,培养学生的辩证唯物主义观、科学精神、创新意识、个性品质，并为学生创造终身学习和可持续发展的条件.

3 课程思政融入“基本不等式”设计路径分析

3.1 凝练教学目标，发展数学素养

基本不等式的学习，是一般到特殊的过程，是学生认知结构一次质的飞跃，能够培养学生演绎推理的数学思维和辩证思维.关于基本不等式的证明，教材有分析法和几何法两种方法.在两种方法的教学中，教师要引导学生从数和形两方面开展探究活动，培养学生数形结合的数学思想及数学能力，培养数学逻辑思维以及科学精神，在探究的过程中提升学生对数学学习的兴趣，提升学生的个性品质.另一方面，从赵爽的弦图和实际问题中抽象出数学模型，和基本不等式在求最值问题中的应用，可以发展学生的数学抽象素养、数学建模素养和数学运算素养；通过赵爽弦图的引入，可以引导学生学习赵爽的科学精神、创新意识和质疑思维，培养学生独立思考的能力，形成良好的个性品质.

3.2 挖掘教学内容，培植个性品格

基本不等式是不等式专题中的重要内容，是学生需要掌握的基础知识.本节开篇从重要不等式进行新课引入，不仅复习了上一节课的学习内容，也回顾了初中所学的完全平方式的旧知，促进学生建构新旧知识的联系，有利于学生科学精神和辩证唯物主义思想的发展.教材首先通过分析法，从代数的角度证明基本不等式，在了解了基本不等式的代数意义后，再通过探究活动的方式得出基本不等式的几何意义，培养了学生从不同角度观察问题的能力，养成了数形结合的思考方式，提升了学生的创新意识和科学精神.通过例题中实际问题的解决，探究利用基本不等式求最值的问题，发展了学生积极向上的学习态度，形成了良好的个性品质，同时也养成了良好的数学学习习惯.

3.3 优化教学方法，渗透科学精神

教师要改进教学方法，借助多样化的教具与信息技术工具进行课堂教学.例如在引入或探究环节，可以通过实例或者古代数学家所探索的问题等，激发学生的学习兴趣，发展学生的科学精神.教学过程中，可以利用“几何画板”为学生演示图形的拼接过程，使学生对基本不等式的理解不仅仅停留在结构和形式上，发展学生的数学核心素养，引导学生理解事物是动态发展的，发展学生的辩证唯物主义观和科学精神.

4 教学过程设计

以下的教学设计以新版高中数学教材人教A版必修一中的《基本不等式》一课进行.

4.1 教学目标

4.1.1 知识与技能

(1)理解基本不等式的内容及证明方法；

(2)掌握运用基本不等式解决最值问题的方法,发展辩证思维.

4.1.2 过程与方法

(1)经历两个正数的算术平均数不小于几何平均数的证明；

(2)体会数学中“形”与“数”的转化特征,形成良好的个性品质.

4.1.3 数学素养目标

(1)探究基本不等式的证明过程,培养逻辑推理能力;

(2)提高数学模型建立的能力,提升科学精神.

4.2 教学重难点

重点:理解从数、形两方面探究基本不等式的证明，提升科学精神

难点:将基本不等式的特点从实际问题的数量关系中抽象出来

4.3 教学过程

4.3.1 情景引入

师:古希腊时期,国王分配土地以长方形的周长为标准:周长相等,则田地面积相等.同学们认为这样分配田地公平吗?

学:在纸上尝试划分田地进行探索,得出不公平

【课程思政点】情景引入实例——科学精神;问题思考环节——数学核心素养、辩证唯物主义思想.

【设计意图】(1)以历史实例为“引”导入所要学习的知识, 学习古人的探索精神并产生质疑，挖掘出其中的思政素材.(2)将具体事物抽象为数学图案,培养了数学抽象素养，培养了辩证唯物主义思想，与课程思政协同把握教学目标.

师:数学史上著名数学家芝诺多鲁斯也发现了这个问题.结合上节课学习的赵爽弦图得出的结论:a2+b2≥2ab.

【课程思政点】解决问题过程——个性品质.

【设计意图】使学生在情景线索与实际探究中产生矛盾,激发学生的思考，培养学生形成良好的学习习惯，学会独立思考并解决问题.

4.3.2 公式探究

师:根据所得出的变式给出基本不等式的概念,并分析代数平均数和几何平均数的含义,得出两个正数的算术平均数不小于几何平均数，并引导学生合作交流完成以下探究活动.

探究一:(作差法)

用不等式的性质证明基本不等式.

【课程思政点】教师引导环节——科学精神;初始探究活动——个性品质.

【设计意图】(1)通过隐性教育的方式教育学生要用辩证的思想来看待问题,要经过科学的证明,并在证明的过程中感受数学文化和数学美的价值.(2)改进教学方法，引导学生在探究活动中开展合作与交流,可以培养学生的奉献精神、表达能力以及人际交往能力等个性品质.

探究二:(几何法)

某城市有一座半圆形的拱桥桥梁坏了,建筑师要修建桥梁,但只知道桥梁底部距桥左右两端的距离为a、b,需求桥梁高度.

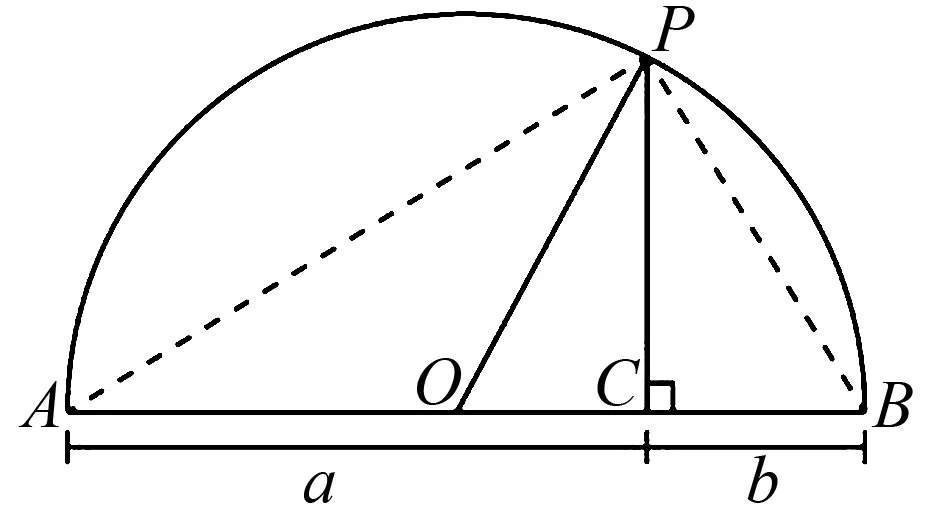
图1

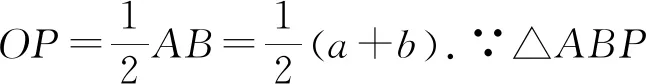
【课程思政点】深入探究活动——辩证唯物主义观;探究活动渗透——爱国主义.

【设计意图】(1)教师把握预设目标，在基本不等式证明过程中培养了学生思维的严谨性和逻辑推理能力;而数形结合、“数”与“形”的转换培养了学生的辩证唯物主义思想，用数学思维看待问题.(2)教学实例的不同选择，使学生有不同的获得感与共通感.在“探究二”中学生们当了一回建筑师,这时可以引申到港珠澳大桥的建造,它是中国人建造起来的世界上最长的跨海大桥,为自己的国家产生自豪感,培养爱国主义精神.

4.3.3 新知应用

学校要新建一个游泳池,其容积是2400m2,深为2m,若池底的造价为140元/m2,池壁的造价为110元/m2,如何设计游泳池的长与宽，使得总造价最少,最少为多少元？

【课程思政点】问题解决环节——辩证唯物主义观.

【设计意图】改进教学方法，通过问题驱动，使得学生将所学的公式应用到实际问题中,体现了理论与实践相结合;通过用所学的新知识解决实际问题,体现了马克思主义与中国特色社会主义指导思想所强调的实践出真知.

师:同学们能总结一下此问题的数学模型吗？

学:在教师的引导下得出结论

【课程思政点】教师引导环节——科学精神;学生思考解决问题环节——数学核心素养.

4.3.4 课堂小结

师:同学们总结一下本堂课学习了什么？

生:基本不等式及其成立条件是“一正、二定、三相等”

师:从哪几个角度出发证明了基本不等式？

生:代数和几何两方面

师:从基本不等式中还得到了哪些结论？

生:一是两个正数的代数平均数不小于几何平均数;二是得到了数学模型

【课程思政点】新知总结环节——个性品质;知识建构环节——辩证唯物主义观.

【设计意图】(1)通过课堂讨论引导学生总结巩固所学的新知识,反思课堂中的问题,有助于学生养成良好的学习习惯,提升个人的品质.(2)总结新知识有利于学生建构新旧知识之间的联系,让学生理解事物是辩证发展的，也逐渐完善数学知识体系和逻辑体系,提升学生的数学素养.

“基本不等式”课堂教学融入课程思政符合《普通高中数学课程标准》的育人要求，落实了以学生发展为本和立德树人的育人要求.这样的设计思路为今后更好地落实课程育人提供了新的借鉴，同时，今后可以继续研究不同课例落实课程思政的一般范式，实现核心素养、核心价值和个性品格的培养和发展.构建更为清晰的发展思路是今后加强课程思政融合的重要研究方向.