Robust adaptive precision motion control of tank horizontal stabilizer based on unknown actuator backlash compensation

Shu-Sen Yuan, Wen-Xiang Deng, Jian-Yong Yao, Guo-Lai Yang

School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing, China

Keywords:Tank Horizontal stabilizer Adaptive control Robust control Backlash inverse

ABSTRACT Backlash nonlinearity inevitably exists in the actuator of tank horizontal stabilizer and has adverse effect on the system control performance, however, how to effectively eliminate its effect remains a pending issue.To solve this problem, a robust adaptive precision motion controller is presented in this paper to address uncertainties and unknown actuator backlash of tank horizontal actuator.The controller handles the modeling uncertainties including parameter uncertainties and unmodeled disturbances by integrating adaptive feedforward compensation and continuous nonlinear robust law.Based on the backstepping method, a smooth backlash inverse model is constructed by combining the adaptive idea.Meanwhile, the unknown backlash parameters of the system can be approximated through the parameter adaptation, and the impact of the actuator backlash nonlinearity is effectively compensated via the inverse operation,which can availably improve the tracking performance.Moreover,the adaptive law can update the disturbance ranges of tank horizontal stabilizer online in real time, which enhances the feasibility in practical engineering applications.Furthermore, the stability analysis based on Lyapunov function shows that with the existence of unmodeled disturbances and unknown actuator backlash,the designed controller guarantees excellent asymptotic output tracking performance.Extensive comparative results verify the effectiveness of the proposed control strategy.

1.Introduction

Tank horizontal stabilizer is an important subsystem of the bidirectional stabilization system, whose main role is to stabilize and drive the turret [1].The current horizontal stabilizer of advanced tank weapons uses a motor servo system as its actuator[2].Although the motor servo system has the advantages of fast response, low noise and high accuracy compared with the traditional electro-hydraulic servo system,its inherent nonlinearity and uncertainty limit the further improvement of its tracking performance [3].At present, the traditional PID controller has been widely applied, but it can only ensure local stability and cannot handle various uncertainties of the system [4-6].As the core subsystem of the fire control system,the precise motion control for horizontal stabilizer has been a problem explored by the scientific research community.

For this reason, in the past decades, many advanced control strategies presented for the precision pointing control of tank stabilizers.Typically, adaptive control (AC) proposed in Refs.[7,8]to handle the effects of the parametric uncertainties.However, little unmodeled disturbances in the system adaptive controller would fail or even lead to system instability.With this in mind, the adaptive robust control (ARC) was developed to handle both parametric uncertainties and uncertain nonlinearities of tank stabilizer[2,9,10].The ARC controller overcame the defects of unstable and poor robustness of the AC controller benefiting from the accurate modeling of the system.In development,to compensate the stronger unmodeled disturbance in the tank stabilizer, an active disturbance rejection adaptive control (ADRAC) was integrated which was based on an ingenious combination with an extended state observer and an adaptive method[11].It is worth noting that active disturbance rejection control is a common approach to deal with model uncertainties, which was proposed by Han [12].This method considers both state and disturbance estimation, and requires little model information except the order of the system model.Its effectiveness has been extensively verified in tank stabilizers[13,14].Regretfully,both ARC and ADRAC can only satisfy tracking error bounded of the system in the presence time-varying disturbances.In Ref.[15], a robust integral of the sign of the error(RISE) controller was developed for tank stabilizer which can handle sufficiently smooth and bounded modeling uncertainties with asymptotic stability.The contribution of this method is that the asymptotic stability of the system is achieved without high gain feedback,which is superior for engineering applications.However,it can only suppress smooth continuous uncertainties well for tank stabilizer, which places a higher demand on the search for a more general control strategy.

Besides the above uncertainties, the actuator of the horizontal stabilizer is a servo motor [16], which inevitably suffers from backlash, dead-zone, saturation and hysteresis [17].This paper focuses on the effect of the unknown actuator backlash which may degrade control accuracy or cause instability.Backlash nonlinearity has always been a critical problem in the electromechanical servo control.Hence, it will be important if the backlash nonlinearity of the tank horizontal stabilizer can be actively compensated based on the design of the control strategy.As presented in Refs.[18,19],there are two main methods to suppress the backlash nonlinearity.The first category is to regard the backlash effect of the actuator uniformly as a composition of an unknown constant gain or unknown time-varying gain input with a bounded uncertainty[10,20-22].Specifically, this approach simply considers the backlash nonlinearity as lumped disturbance of the system, so the backlash impact can be suppressed through the robust controller.However, this method does not accurately analyze and actively compensate the backlash nonlinearity, which greatly affects its steady-state control accuracy.Although this approach is easy to implement,it may lead to system instability due to the use of highgain feedback in the nonlinear robust term.Another way realizes the active compensation of the backlash by constructing the inverse function [19,23-25].The main idea of the inverse function is constructing an inverse compensator ingeniously to make the compensation error small enough.Currently, the active compensation method based on backlash inversion has not been implemented in tank stabilizers.However,it is widely adopted in various fields owing to its superiority, such as robot system [19], robotic manipulator system[24],and vibrating coupled vessel-riser system[25].Moreover, combined with the special operational environment of tank weapons, the effect of backlash nonlinearity can be more dramatic in the vibration state.What is really needed for the horizontal stabilizer is a simple and efficient controller not only for the active compensation of backlash nonlinearity but also to overcome the influence of various complex external disturbances.This will be a very challenging research subject.

In this paper,the aforementioned issues are addressed.A novel robust adaptive precision motion controller is presented for tank horizontal stabilizer exposed to modeling uncertainties and unknown actuator backlash, combining the nonlinear robust construction in Ref.[26]with adaptive idea through backstepping technology.Meanwhile, the influences of actuator backlash are attenuated via applying a smooth backlash inverse in Ref.[19].The unknown backlash parameters and other model uncertain parameters of the system are approximated by the derived parametric adaptive functions.Furthermore,the unmodeled disturbances and the other model errors resulting from the smooth backlash inverse compensation are eliminated by the continuous nonlinear robust term.Even in the presence of various uncertainties, stability analysis shows that tank horizontal stabilizer can obtain perfect asymptotic tracking performance.

The main contributions of this article are reflected in the following five aspects:

(1) A novel smooth backlash inverse model is proposed to achieve active compensation for the unknown actuator backlash of tank horizontal stabilizer.

(2) The adaptive feedforward compensation method combined with the nonlinear robust form can simultaneously handle the unknown actuator backlash, parametric uncertainties and unknown bounded disturbances.

(3) Since the adaptive law can estimate the upper bound of the system disturbance online which avoids the high gain feedback and the requirement of exact bound for disturbances is eliminated.

(4) The superiority of the proposed controller is verified by extensive comparative experimental and co-simulation results in tank horizontal stabilizer with an artificial backlash.

(5) To the best of our knowledge, this paper is the first to apply continuous control input to achieve asymptotic tracking performance with unknown actuator backlash compensation for the moving tank horizontal stabilizer.

This paper is arranged as follows.Section 2 shows the problem formulation and dynamic models.The controller design and the unknown actuator backlash compensation are given in Section 3.Extensive comparative experimental and co-simulation results from Section 4.Conclusions can be found from Section 5.

2.Problem formulation and dynamic models

In this paper, the tank horizontal stabilizer under study is presented in Fig.1.Its main structure includes turret, servo motor,multi-stage gear mechanism, and seating system.The horizontal stabilizer uses the servo motor as its actuator,and the input voltage generates the armature current,which interacts with the excitation flux in the armature circuit to generate the electromagnetic torque to overcome the turret load.Eventually the servo motor and multistage gear mechanism follow the turret horizontal direction to rotate synchronously.

The dynamic model of the horizontal stabilizer load

whereqis the angular displacement,is the angular velocity of the turret in the horizontal direction;Jdenotes the rotational inertia of the load with respect to the turret slew axis,T1denotes the output torque of the gear mechanism,Bdenotes the coefficient of viscous friction,d(t) denotes the modeling errors and external disturbances.

The torque balance equation of the actuator servo motor

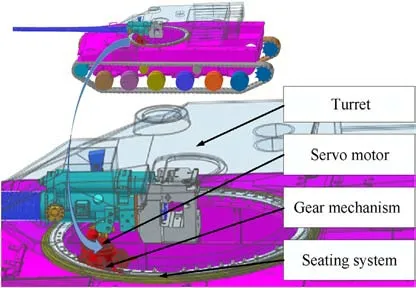
Fig.1. Schematic diagram of the tank horizontal stabilizer.

whereqmis the angular displacement,is the angular velocity,is the angular displacement of the servo motor;Jmdenotes the rotational inertia of the servo motor,Bmdenotes the friction coefficient of the motor shaft,Tmdenotes the input torque of the gear mechanism,Tedenotes the electromagnetic torque, which is proportional to the armature currentiof the servo motor.Hence, we have

in whichktdenotes the torque coefficient of the servo motor.

Considering the input backlash of the actuator,then the voltage balance equation of the servo motor can be expressed as

whereRis the motor armature resistance,Lis the motor inductance,keis the counter-electromotive force coefficient.BL(u) represents the backlash characteristics of the actuator, which can describe the static mapping relationship between the actuator backlash and the control input voltageuas follows:

whereVBL(u) represents the backlash nonlinearity of the actuator,the slopesis a positive constant;brandblare constant parameters satisfyingbr>0 andbl＜0,which together determine the width of the backlash;BL(u(t-)) represents the control output signal at the previous moment, which means that the control input signal has not changed.As shown in Fig.2 is the schematic diagram of the actuator backlash nonlinearity.

Remark 1.The models describing the backlash nonlinearity mainly include the hysteresis model,the dead zone model and the vibrational impulse model.Combined with the actual characteristics of the tank horizontal stabilizer,the hysteresis model is applied in this paper to characterize the backlash nonlinearity between the input and output of actuator.Meanwhile, based on the analysis of Fig.2,assumption of the hysteresis model is that the output of the driven part is constant when the driving part of the system is in the backlash period.

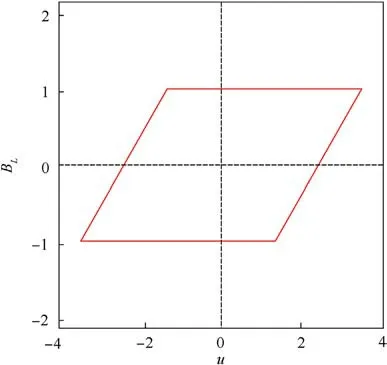
Fig.2. Backlash nonlinearity.

In a practical tank horizontal stabilizer,the electrical constantL/Ris always small (compared to the mechanical time constant J(q)/B),then the electrical transient decays very rapidly andLdi/(Rdt)is very close to zero [27].Hence, combining Eq.(3), we have

As the horizontal subsystem adopts a multi-stage gear mechanism for deceleration, the mathematical analytical relationship between the input torque Tmand the output torqueT1of the multistage gear mechanism can be described as

whereNis the transmission ratio of the multistage gear mechanism, dm(t) is the unmodeled error of the multistage gear mechanism transmission process.

Then,the output torqueT1of the gear mechanism is represented as

Focusing onT1,and taking it into Eq.(1),the dynamic equation of tank horizontal stabilizer can be expressed as

Remark 2.The integrated dynamical Eq.(10) of the tank horizontal stabilizer is derived by combining the dynamics of the turret system (1) and the dynamics of the actuator motor servo system(2).It is a nonlinear electromechanical coupled system.

The following state variables x=［x1，x2］T=［q，］Tare defined to describe the angular displacement and angular velocity of the tank horizontal stabilizer.Hence,the state space form of Eq.(10)is given as

We expect to synthesize a bounded control input u that will makex1accurately tracks the given desired motion trajectoryx1d,when the system is subject to model uncertainties and unknown actuator backlash.

3.Robust adaptive controller design

3.1.Backlash compensation

In order to suppress the adverse effect of unknown actuator backlash in the tank horizontal stabilizer,a compensation strategy based on the inverse model of backlash is proposed in this paper,as shown in Fig.3.A novel smooth backlash inverse model is described as

It is important to mention that the traditional compensation method with backlash inverse is to calculate the inverse of Eq.(5)directly.However, such an inverse model is discontinuous and cannot be combined with the classical backstepping technology.Therefore, a novel smooth backlash inverse model is presented in this paper to address the unknown actuator backlash of the tank horizontal stabilizer.It is not only easy to design the controller but also avoid the chatter of the control input signal.

Since the parameterss,brand blare unknown in the controller design, and BL(u) cannot be measured in practical applications.In order to parameterize the backlash characteristics linearly, the unknown backlash parameters ϑ=［ϑ1，ϑ2，ϑ3］Tare defined,where,the linear parameterized backlash modelBLacan be given as

Considering ϑ is unknown, defineas the estimated value of ϑ which will be achieved later by the designed adaptive law.Then the designed adaptive backlash inverse model is

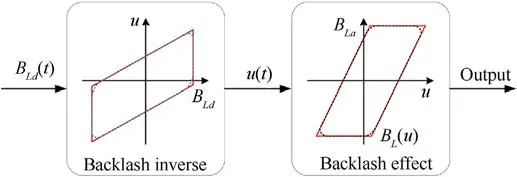
Fig.3. Schematic diagram with backlash inverse.

wheredb(t) represents the unmodeled error caused by nonparameterization which is bounded.

Except for the unknown actuator backlash parameters,the tank horizontal stabilizer also undergoes the influence of other parameter uncertainties.Therefore,this paper also explicitly considers the effect of unknown parameters of the system such as the viscous friction coefficientB, which is defined as θ =B.Further, in combination with Eq.(15), the state space Eq.(11) is represented as

whereD(t) =dm(t)-d(t)-(ktN/R)db(t) which represents the lumped disturbance of the system.For practical tank horizontal stabilizer,there are the following reasonable assumptions:

Assumption 1.The desired motion trajectoryx1d(t) is second order continuously differentiable and its derivatives are all bounded.

Assumption 2.The time-varying lumped disturbanceD(t) is bounded satisfies |D（t）|≤δ, where δ is an unknown constant.

Assumption 3.The range of unknown parameters ϑ and θ are known, i.e.,

where ϑmin= ［ϑ1min，ϑ2min，ϑ3min］T, ϑmax= ［ϑ1max，ϑ2max，ϑ3max］T,θminand θmaxare known.For practical backlash model,the parameters≠0,therefore,we assume that in the controller design process ϑ1≠0.

To pledge the estimation of the unknown parameter vectors θ and ϑ are always within the known extent in Eq.(17).Combining Assumption 3, two discontinuous projections is expressed as Ref.[28].

wherei= 1, 2, 3.Applying the two adaptation laws given by

where Γϑand Γθare non-negative diagonal adaptation rate matrices,τϑand τθare adaptation functions to be constructed later;for arbitrary adaption functions τϑand τθ,the projection mappings employed in Eq.(20) guarantee

Remark 4.In Assumption 2, although the time-varying disturbanceD(t) has an unknown bound, it can be estimated via the adaptive law of subsequent synthesis.Since for the actual tank horizontal stabilizer, both the unmodeled disturbanced(t) of the system and the transmission errordm(t) of the gear reduction mechanism are naturally bounded.Meanwhile,the boundedness ofdb(t)was analyzed in Ref.[23].Therefore,we can know thatD(t)is bounded, i.e., Assumption 2 is reasonable.

3.2.Controller design

The design of the developed controller based on the backstepping method is expected to accurately track the target trajectory with the tank horizontal stabilizer containing parametric uncertainties and unmodeled disturbances.

Step 1.Give a set of error variable as

wherez1represents the tracking error,the time derivative ofz1can be given by

Step 2.Letz2≜x2-α1be the discrepancy betweenx2andx2eq,then the virtual control law α1is designed as

wherek1is a non-negative feedback gain.Further the derivative ofz1with respect to time can be achieved

Because the transfer function of Eq.(42) isz1(s) =G(s)z2(s),G(s) = 1/(s+k1), makingz1small enough or converging to zero is equal to keepingz2small enough or converging to zero.With this end in view, the next goal is to ensure thatz2is sufficiently small.Step 3.Noting Eq.(16) and differentiating the errorz2with respect to time, we have

Noting the structure of Eq.(27),to achieve the excellent tracking performance, a realistic control input needs to be designed.Actually,BLDis applied as the control input that stabilizes the tank horizontal stabilizer and avoids unknown actuator backlash.Then the robust adaptive control law forBLDis designed as

wherek2andk2sare positive feedback gains, ω（t） > 0 is an integrable function andis the estimation ofD(t).

In Eq.(28),BLDadenotes a regulable model compensation term for improving the tracking performance with online parameter adaptive;BLDsdenotes a robust control term,BLDs1denotes a linear robust control term that makes the nominal model of the tank horizontal stabilizer reliable, andBLDs2denotes a nonlinear robust control term to alleviate the effect of the lumped disturbance.

Substituting Eq.(28) into Eq.(27), we have

Combined with the novel smooth backlash inverse model of Eq.(12), the final actual control input of the tank horizontal stabilizer can be given by

Assumption 4.The function ω（t） in Eq.(30) conforms to the following conditions:

where μiandare positive constants.

Remark 5.Observing Eq.(28), the nonlinear robust control termBLDs2derived in this paper considers the upper bound estimatefor the unmodeled disturbance of the tank horizontal stabilizer.It means that the exact upper bound for the unmodeled disturbance does not need to be known in advance for the controller design,further enhancing the practicality of the controller.In addition,the final robust adaptive controller is bounded and continuous due to the use of a glossy tanh function and a positive integrable function ω（t）.Compared with other discontinuous controllers,the proposed controller in this paper is more suitable for engineering practice.

3.3.Main results

Theorem 1.Based onAssumption 1-4,in conjunction with the following adaptation laws:

whereΓθandΓϑare positive definite diagonal adaptation rate matrixes,λis an adaptation rate gain.Next,the k1,k2,and k2s are selected to be large sufficient so that the matrixΛis positive definite

By this,the robust adaptive control lawEq.(28)with actuator backlash compensation proposed in this paper can achieve an asymptotic tracking performance,i.e.,z1→0as t→∞and ensure that all signals of tank horizontal stabilizer are bounded.

Proof:SeeAppendix A.

Remark 6.Based on the theoretical results,the following summary can be made:the controller proposed in this paper can obtain perfect asymptotic tracking performance for tank horizontal stabilizer with parameter uncertainties,unmodeled disturbances and unknown actuator backlash.Meanwhile,the convergence rate will be improved via enhancing the gains k1,k2and k2s.Having such superior tracking performance is expected for a tank horizontal stabilizer with high precision motion control.

4.Co-simulation and experimental results

4.1.Co-simulation results

To verify the precision tracking performance of the proposed robust adaptive controller for tank horizontal stabilizer, a cosimulation experimental platform has been set up, and its principle structure is shown in Fig.4.In the modeling process,the multibody dynamic model of moving tank horizontal system is established in Recurdyn,the actuator of system is modeled in Simulink.The following parameters of system are:J= 10526.3 kg·m2,Jm= 0.002 kg·m2,Bm= 0.0012 N·m·s/rad,kt= 1.89 N·m/A,R=0.607 Ω,L=5.88 mH,ke=1.09 V·s/rad.The output torques of the actuator are loaded onto the motor output gear in Recurdyn through a data interaction interface between Simulink and Recurdyn.

Moreover,to verify the effectiveness of the presented controller,the following artificial backlash is inserted in the actuator of the tank horizontal stabilizer by the control algorithm for cosimulation, in which several key parameters are set ass= 1,br= 0.7,bl= -0.7.Hence, it can be expressed as

Furthermore,to evaluate the validity of the comparison control methods,the below three metrics applied as evaluation criteria,i.e.,the maximum errorMe, average error μ, and standard deviation error б are utilized,the definitions of them can be seen in Ref.[29].To simplify the co-simulation and experimental validation, we assume that the slopesof the backlash model is a known parameter.The following three controllers are compared to illustrate the validity of the robust adaptive controller proposed in this article.

(1) RACB: This is the robust adaptive controller combined with unknown actuator backlash compensation Eq.(28)proposed for tank horizontal stabilizer.The given control gains for system are as follows:k1=18,k2= 45,k2s= 35 which are resolved by online adjustment to promote performance.According to Assumption 4, we choose ω(t)=10000/(1+t2),and the other parametersn1=1,s=1.Some initial values of parameter estimates are given as（0） = ［0］T, ［，］T=［0，0］Tand,（0） = ［0］T.Setting the following parameter adaptation rates Γθ= diag｛15｝,Γϑ= diag｛2，2｝,λ = 8.

(2) RAC: This is the robust adaptive controller that ignores unknown actuator backlash compensation for tank horizontal stabilizer.That is to say, it can prove the validity of the developed backlash inverse model.Some relevant parameters are kept constant with RACB, which can ensure a convincing comparison.

(3) ACB: This is the adaptive backstepping controller, which differs from the RACB controller is that it is without the nonlinear robust term of tank horizontal stabilizer.This comparison is intended to present the advantage of the nonlinear robust term in suppressing disturbances.It has the same controller parameters as RACB.This will ensure that the comparison is fair enough.

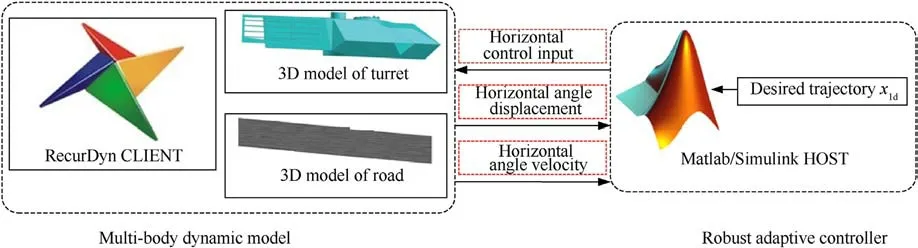
Fig.4. Principle structure of co-simulation.

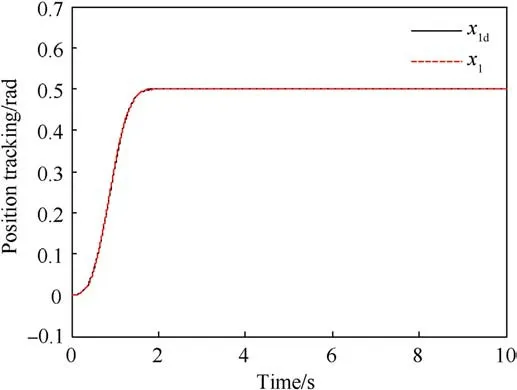
Fig.5. Position tracking Performance of RACB in co-simulation.

The following smooth desired motion trajectory is given for the tank horizontal stabilize:x1d(t)=0.5(1-exp(-t3))rad.This condition can not only examine the static tracking performance, but also verify the stabilization accuracy of the system.The corresponding co-simulation results are shown in Fig.5-Fig.8.The performance indices for the last 5 s are presented in Table 1.Specifically, the position tracking performance for horizontal stabilizer with the proposed RACB controller can be observed in Fig.5, which reflects that the system can accurately track the desired trajectory.The comparative tracking errors of RACB,RAC and ACB are exhibited in Fig.6, and in Table 1 the performance indices are obtained.As presented, the RACB controller obtains the best tracking performance relative to the other controllers.The tracking performance of RAC is worse than RACB because the backlash compensation of the unknown actuator is not considered, which proves the validity of the developed backlash inverse model for suppressing the backlashnonlinearity.Although the ACB controller employs the same backlash inverse compensation as RACB, the strong robustness of the nonlinear robust term in RAC makes its tracking error smaller than that of ACB.In summary, combining Fig.6 and Table 1, it is clear that the RACB has the most superior transient and steadystate tracking performance.Fig.7 presents the unknown parameters and upper bound estimates of the tank horizontal stabilizer under the action with the RACB controller.The control input and driving torque are shown in Fig.8, which are continuous and bounded.

Table 1Performance indices of tank horizontal stabilizer after 5 s in co-simulation.

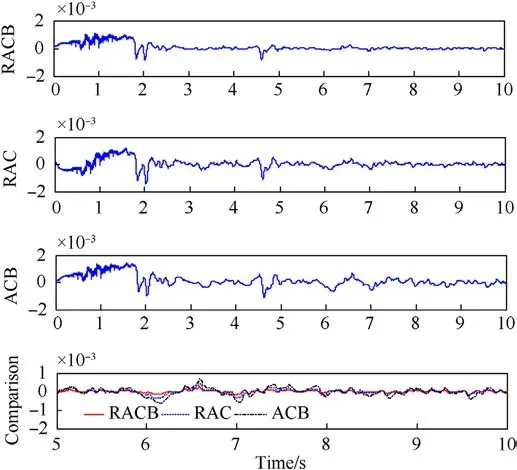
Fig.6. Comparative tracking errors of tank horizontal stabilizer in co-simulation.

4.2.Experimental results

Fig.7. Unknown parameters and upper bound estimates of RACB in co-simulation.

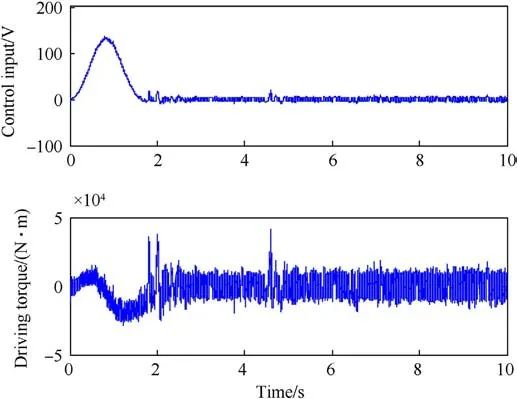
Fig.8. Control input and driving torque of RACB in co-simulation.

Fig.9. Experimental platform of tank horizontal stabilizer.

To further attest the effectiveness of the proposed controller,an experimental platform of the tank horizontal stabilizer is established as presented in Fig.9.The experimental platform includes the experimental module and the measurement and control module.The experimental module mainly includes inertial load of tank horizontal stabilizer system, an actuator motor, bracket, etc.,and is equipped with a rotary encoder and torque sensor.The measurement and control module mainly contain monitoring software and real-time control software with an Advantech PCI-1723 card and a Heidenhain IK-220 counter card.The control program of the lower computer is written by discrete C++code on the basis of the real-time operating system, the corresponding visual monitoring software of the upper computer is constructed through LabWindows CVI.Setting the sampling time to 0.5 ms.

The artificial actuator backlash based on the experimental platform is constructed by control algorithm to be the same as Eq.(34).Meanwhile, three controllers, RACB, RAC and ACB, are also selected for comparison to describe the superiority of the developed controller.

Fig.10. Comparative tracking errors in case 1.

Table 2Performance indices after 5 s in case 1.

During the experiments,the control gains of RACB controller are set ask1=110,k2=100,k2s= 0.5.We also choose ω(t) = 10000/(1+t2), and the other parametersn1= 1 ands= 1.Some initial values of parameter estimates are also given as（0） = ［0］T,［（0），（0）］T= ［0，0］Tand（0） = ［0］T.The parameter adaptation rates are set as Γθ= diag｛12｝, Γϑ= diag｛4，4｝, λ = 12.The relevant parameters of RAC controller are the same as RACB controller,but the compensation of unknown actuator backlash is not considered.The comparison between ACB controller and RACB controller can verify the ability of nonlinear robust term to suppress the system disturbance, and its controller parameters are consistent with RACB considering the fairness of comparison.

In case 1, the desired motion trajectory is given by:x1d(t) = 0.5(1-exp(-t3)) rad.This case can verify the steady-state tracking performance of the proposed control strategy.The comparison results of the three control strategies are shown in Fig.10,and Table 2 exhibits the performance indices after 5 s.It is not difficult to find that the developed RACB controller still achieves the best control effects in terms of transient and steady-state tracking performance.The RACB improves the stabilization accuracy of the horizontal stabilizer by 27.7% and 45.5% compared with the RAC and ACB controllers, respectively.Although all three controllers show bias,observing the trend of the tracking error with the RACB controller reveals that it has the characteristic of asymptotic convergence.Therefore, it is once again verified that RACB has a perfect backlash compensation effect and a strong robustness with the above experimental results.The disturbance upper bound estimations and unknown system parameter estimations are collected in Fig.11.Due to the parametric adaptive law, the unknown parameter estimation of the system converges gradually.Meanwhile, the upper bound estimation of disturbance also converges gradually to a constant value.The control input is presented in Fig.12, which is continuous and bounded.

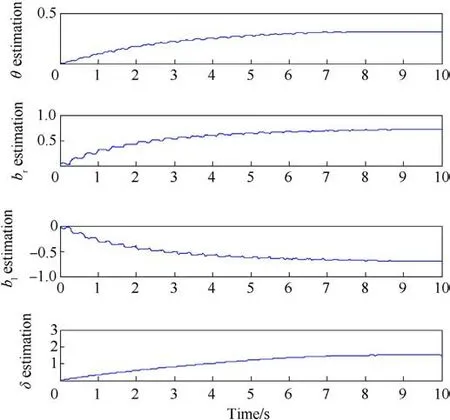
Fig.11. Unknown parameters and upper bound estimates of RACB in case 1.

Fig.12. Control input of RACB in case 1.

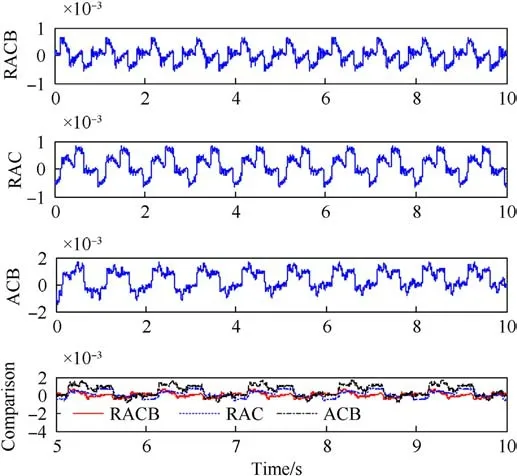
Fig.13. Comparative tracking errors in case 2.

Table 3Performance indices after 5 s in case 2.

In case 2,the dynamic tracking performance with the proposed controller for the tank horizontal stabilizer is further verified.The desired motion trajectory is given asx1d(t) = 0.5sin(2πt) (1-exp(-t3))rad.The comparative tracking errors of the three controllers are collected in Fig.13.The performance indices after 5 s are summarized in Table 3.As presented,the proposed RACB controller still achieves the best tracking performance compared to the other two controllers,verifying its superiority.In the process of dynamic tracking,the performance indices of the three controllers in case 2 are worse than those in case 1.This shows that the dynamic tracking process will put forward higher demands for tank horizontal stabilizer.In conclusion,the results of case 2 again illustrates the better backlash compensation effectiveness and stronger robustness of the proposed RACB controller.

5.Conclusions

In this article, a practical robust adaptive precision motion controller considering unknown actuator backlash compensation is presented for tank horizontal stabilizer subject to parametric uncertainties, unmodeled disturbances and backlash nonlinearity.To obtain attractive results,a novel smooth backlash inverse model is constructed to eliminate the adverse effect of unknown actuator backlash.Meanwhile, the adaptive laws are synthesized based on the backstepping technique to estimate the unknown system parameters and backlash parameters in real time.Furthermore, a nonlinear robust term consisting of a smooth tanh function and a positive integrable function is constructed to handle the unmodeled disturbances of the system.The controller achieves active compensation of the unknown actuator backlash for the tank horizontal stabilizer.By analyzing the stability, the proposed controller can achieve asymptotic tracking performance theoretically when facing unknown actuator backlash and modeling uncertainties.Extensive comparative co-simulation and experimental results verify the superiority of the proposed control approach.As future work, robust adaptive controller combined with neural network,dynamic surface technique[30],and disturbance observe[31]are worth being developed for tank horizontal stabilizers.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

This work was supported in part by the National Natural Science Foundation of China under Grant 51905271, Grant No.52275062 and Grant No.52075262

Appendix A

Proof of Theorem 1: Choosing the following Lyapunov function

Combining with Eq.(26) and Eq.(29), we have

From Assumption 2,we can know that the time-varying lumped disturbanceD(t) is bounded satisfies |D（t）|≤δ.Hence, we have

By observing Eq.(A5),|z2|is constructed in the following form

To facilitate further derivation, and applying the following inequality:

Based on Eq.(A7), Eq.(A6) can be described as

Then taking Eq.(A9)into Eq.(A5), we have

Combining Eq.(A7) again, we have

Thus, based on Eq.(A8), we obtain

According to the adaptive laws designed in Eq.(32), Eq.(A12)can be rewritten as

Noting the matrix Λ is positive definite,we have

where z = [z1,z2]T,λminis the minimal eigenvalue of Λ andWis a nonnegative function.Calculating the integral of Eq.(A7), and consideringAssumption 4to obtain

Noting Eq.(A8), it can be inferred thatV（t）∈L∞andW∈L2.Observing the definition of Eq.(A1),we know thatz1,z2,,,are bounded.Hence,,,are also bounded.Considering Assumption(1) and (2), it can be found that the statexis bounded, and combined with assumption(4),it is known that the actual control inputuis also bounded.Then we can know that all signals of the closedloop system are bounded.Based on the dynamics ofz1andz2,it is convenient to conclude thatis bounded,and thusWis uniformly continuous.By applying Barbalat's lemma[32],W→0 ast→∞,i.e.,z1→0 ast→∞, which leads to the results in Theorem 1.