Mechanical behavior of entangled metallic wire materialspolyurethane interpenetrating composites
Xiao-yuan Zheng , Zhi-ying Ren ,*, Hong-bai Bai , Zhang-bin Wu ,**,You-song Guo
a College of Mechanical Engineering and Automation, Fuzhou University, Fuzhou, 350116, China
b Institute of Metal Rubber & Vibration Noise, Fuzhou University, Fuzhou, 350116, China
c Gongbang Vibration Control Technology Co., Ltd, Jiangsu, Jiangyin, 214431, China
Keywords:Entangled metallic wire material Composites materials Damping property Stiffness Fatigue characteristics
ABSTRACT Composite materials exhibit the impressive mechanical properties of high damping and stiffness, which cannot be attained by employing conventional single materials.Along these lines, a novel material architecture is presented in this work in order to fabricate composites with enhanced mechanical characteristics.More specifically, entangled metallic wire materials were used as the active matrix, whereas polyurethane was employed as the reinforcement elements.As a result, an entangled metallic wire material-polyurethane composite with high damping and stiffness was prepared by enforcing the vacuum infiltration method.On top of that,the mechanical properties(loss factor,energy consumption,and average stiffness) of the proposed composite materials were characterized by performing dynamic tests,and its fatigue characteristics were verified by the micro-interface bonding,as well as the macro-damage factor.The impact of the density, preloading spacing, loading amplitude, and exciting frequency on the mechanical properties of the composites were also thoroughly analyzed.The extracted results indicate that the mechanical properties of the composites were significantly enhanced than those of the pure materials due to the introduction of interface friction.Moreover, the average stiffness of the composites was about 10 times the respective value of the entangled metallic wire material.Interestingly, a rise in the loading period leads to some failure between the composite interfaces, which reduces the stiffness property but enhances the damping dissipation properties.Finally,a comprehensive dynamic mechanical model of the composites was established,while it was experimentally verified.The proposed composites possess higher damping features,i.e.,stiffness characteristics,and maintain better fatigue characteristics,which can broaden the application range of the composites.In addition, we provide a theoretical and experimental framework for the research and applications in the field of metal matrix composites.
1.Introduction
The entangled metallic wire material (EMWM) is a porous damping material that is generally made of a series of coiled metal wires with various sections embedded and hooked to achieve a spatial network structure [1-5].EMWM has attracted great attention due to its superior structural(high porosity,large working surface area, sound absorption, sealing, and damping), as well as non-structural characteristics (anti-corrosion and elasticity).For that reason, it has gradually become an excellent candidate for ordinary rubber products [6-11].Additionally, extensive research has been conducted on the preparation and energy consumption mechanism of EMWM.More specifically, Bai et al.[12,13]investigated various winding and laying methods, which provide a reference for the mechanized and large-scale production of EMWM.Ren et al.[14]employed the ANSYS software to achieve a virtual preparation of the EMWM and addressed the complex problem of the EMWM process simulation, which is of great importance for the practical fabrication of EMWM.Furthermore,Ao et al.[15,16]explored the energy mechanism of the EMWM and concluded that the dry friction between the micro-element springs within the EMWM is the primary reason for its improved damping and energy dissipation characteristics.EMWM has been used in the field of defense technology as its outstanding advantages.In Russia,EMWM was used for the first time for the liquid nitrogen end contact seal of the HK-89 gas turbine engine, and achieved a good sealing effect [17].Ao et al.[18]applied EMWM to aero-engine pipeline, and the results showed that EMWM as damping material can better solve the vibration problem of engine pipeline.Li et al.[19]employed an EMWM component to take the place of rubber in the breechblock rod of certain self-propellant artillery gun and it verified that the EMWM buffer was much superior than ordinary rubber buffer.Gao et al.[20]conducted an antipenetration test on EMWM sandwich composite target.The results proved that the multiple strike resistance of composite armor was improved and avoid spacecraft failure of nuts during pyrotechnic separation.In addition, the application of metal rubber,such as rotor bearing [21,22], building structure [23,24], ship vibration reduction [25-27]has been also extensively investigated.
Although EMWM exhibits excellent stiffness and strength characteristics, severe problems arise when it is used in a special service environment.More specifically, as far as applications with high damping performance requirements, their low damping performance does not permit the achievement of a satisfactory vibration reduction effect.For that reason,in order to obtain elevated stiffness characteristics, the density of the EMWM needs to be increased, which strongly affects the damping property and limits the potential applications.By considering that a single damping material is unable to meet the stringent requirements,the damping composite materials have gradually emerged as a quite popular research topic [28,29].At present, the composites materials with high damping and stiffness characteristics are primarily aluminum foam-based matrix composites.Liu et al.[30]reported the method of percolation to fill the reinforced polyurethane(PU)into open-cell aluminum foam for formulating aluminum foam composites material.Due to the viscoelasticity of the PU materials and the friction between the aluminum foam skeleton and PU, the composites possess significantly higher damping properties.In addition, the matrix aluminum foam can provide enhanced load-bearing properties.Bao et al.[31]studied the mechanical properties of the foamed aluminum/polyurethane composites under enforcing intermittent and repeated cyclic compression processes.Alavi et al.[32]investigated the impact of foam filling of honeycomb panels on their plastic behavior and mechanical properties.Also, the impact of various experimental parameters including the cell size,the cell walls thickness and the thickness of the panel on the mean crushing strength, energy absorption capacity and wavelength of the folds were also investigated.In addition, Zhang et al.[33]recently presented a technique for the three-dimensional reconstruction of the Materialise's Interactive Medical Image Control System (MIMICS) with an adjacent mask based on the Digital Imaging and Communications in Medicine(DICOM)data protocol for the spherical open-cell aluminum foam-polyurethane composites.The acquired experimental results indicate that the modeling method is effective for the quasi-static compression test of the aluminum foam-polyurethane composites.The main applications of composites are shown in Fig.1.
In addition,several other polymer fillers have been explored by the scientific community, such as silicone rubber [34-36], poxy resin [37-39], polystyrene [40-42], etc.However, the observed mechanical properties of the silicone rubber are poor,whereas the epoxy resin is prone to the stress concentration effect after the curing process [43].On the other hand, polyurethane exhibits the advantages of enhanced tear and wear resistance, high elasticity,and good damping performance[44].Besides PU have outstanding bonding properties, which can be processed into the liquid phase before the curing procedure.Such advantages render PU as an ideal material for the fabrication of novel porous composites material[45,46].
Along these lines, inspired by the concept of the porous reinforced composites material, an EMWM-PU composites with excellent energy absorbing properties and load-carrying capabilities is proposed in this work.Furthermore, the compressive mechanical properties, as well as the hysteresis behavior of the EMWM-PU composites are thoroughly investigated.Initially, the EMWM-PU composites were prepared by employing the vacuum infiltration filling process, where a spatial network structure with pore characteristics was used as the host matrix and a twocomponent polyurethane as the reinforcement element.Then, the impact of both the density of the EMWM and the key experimental parameters on the energy consumption and stiffness of composites is analyzed by associating the energy dissipation form of the composites with the contact states of the helix wires and the interfacial friction.Subsequently, the acquired scanning electron microscopy (SEM) results reveal that the composites possess good fatigue resistance.Also, the damage factor of the composites was determined after enforcing 200000 consecutive fatigue tests.Finally, a nonlinear constitutive dynamic model of the EMWM-PU composites was established to predict the influence of the various experimental parameters on the dynamic properties of the composites.As a novel material with high damping and great stiffness, the EMWM-PU composites can be applied for various applications where an enhanced physical impact,a reduction of the vibration reduction, and load-bearing characteristics are required.On top of that, our work paves the way for the design of novel applications of composite materials.

Fig.1. Main applications of the composite materials: (a) Aluminum foam-polyurethane composite; (b) Foam-ceramic composite; (c) Metal rubber-magnesium composite.
2.Preparation of the composite materials
2.1.Fabrication technologies of the entangled metallic wire materials
The wires within the EMWM are intertwined to form a complex spatial network structure.More specifically, the fabrication procedure of the EMWM is summarized in the following four steps:(i)Initially, the mental wire was encircled into a tight helical coil by using a special winding device (as illustrated in Fig.2).In general,the wire diameter was 0.10-0.30 mm, whereas the larger wire diameter possesses a higher mechanical strength.Herein, austenitic stainless steel of 304 (06Cr19Ni10) with a diameter of 0.3 mm was selected as the raw material,which is a typical and commonly used material for the fabrication of the EMWM.The detailed performance parameters of the selected materials are presented in Table 1.As far as the diameter of the coil (d1) is concerned, it was close to 5-15 times the wire diameter.
(ii)Subsequently,the initial helical spiral wire was stretched to a spring-like structure with an equal pitch by using a numerical control blank entangle device(Fig.3(a)-Fig.3(c)).The pitch of the spiral coil was approximately the same as the diameter of the spiral coil (P = D) in order to ensure an effective meshing between the spiral coils and thus improve the total stability of the structure.
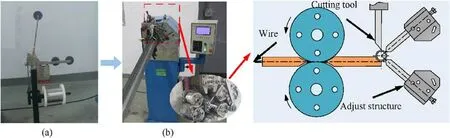
Fig.2. Process of the winding helical coil (a) conveying the wire structure, and (b) entangling the helical spiral wire.

Table 1Performance parameters of the 06Cr19Ni10 material.
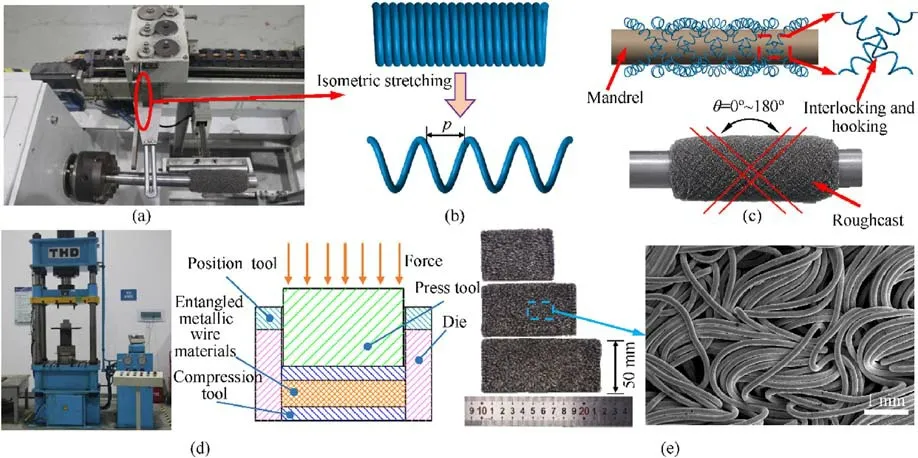
Fig.3. Fabrication procedure of the EMWM:(a)Entangle equipment;(b)Tensioning the wire into a suitable pitch;(c)Entangling the coiled wires;(d)Compression forming;(e)The specimens of the EMWM.

Table 2Preparation parameters of EMWM.
(iii) A compressive forming process was enforced to the rough sample in a customized mold by using a hydraulic press in order to obtain the shaped product(as illustrated in Fig.3(d)).Furthermore,in order to acquire forming shape accuracy and structure consistency,a proper holding time of 60 s at the maximum forming load stage was selected for ensuring the stability of the plastic deformation of the material.Then, the EMWM structure with a certain design shape was obtained (Fig.3(e)).
(ix) Notably, the ultrasonic cleaning process should be used to remove slight contaminants such as steel scurf and lubricate oil and ensure that there are no impurities on the surface of the steel wire in the subsequent fabrication steps.In other words,the two-phase interface should remain intact.
Herein, four kinds of EMWM with different densities were prepared(1.4 g/cm3,1.6 g/cm3,1.8 g/cm3,and 2.0 g/cm3).Moreover,the EMWM samples of each density were prepared with lengths of 68 mm,88 mm,and 112 mm for application in the actual structural pipeline coatings.Every three pieces of the materials with different lengths were superimposed together with the upper and lower parts of the pipeline coating.The selected forming parameters of the EMWM materials that were employed in this work are listed in Table 2.
2.2.Preparation of the EMWM-PU composites
By considering the porous characteristics of the EMWM, the application of the traditional extrusion method will destroy its three-dimensional porous structure.Therefore, a vacuum infiltration method was used in this study, whereas the preparation process is disclosed in Fig.4.The PU is a two-component material comprising of component A and component B.In order to maintain an enhanced material quality, the PU was obtained by mixing the component A with component B in the mass ratio of 1:1.All the components were purchased from the same corporation(Shenzhen Dazhou Chemical Ltd.China).Table 3 highlights the mechanical properties of the PU at room temperature.
Fig.5 displays the SEM image of the as-prepared composite materials.As it can be ascertained, a good bonding state at the interface between the wires and the PU was attained, indicating that the vacuum infiltration process exhibits certain feasibility and can ensure that the PU is properly filled into the pores of the EMWM.As is divulged in Fig.5, a certain number of extrusion contact states between wires in the composites materials can be observed.Therefore,when the EMWM-PU is subjected to external forces, the extrusion friction between the wires is anticipated to play a crucial role in the damping and energy dissipation characteristics.However,a small amount of detachment between the wire and the PU still takes place within the composites.
Since EMWM and PU are the two components of the composites,the mass ratio of the EMWM to the EMWM-PU can be used for the characterization of the composites.The employed calculation method is described as follows:
wherem1andm2are the masses of the EMWM and PU respectively.Table 4 provides the mass ratio of the prepared EMWM-PU composites.
3.Experimental
3.1.Mechanical system for the dynamic testing process
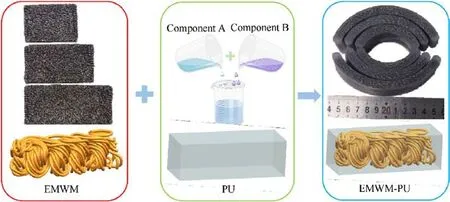
Fig.4. Preparation process of the EMWM-PU composites.
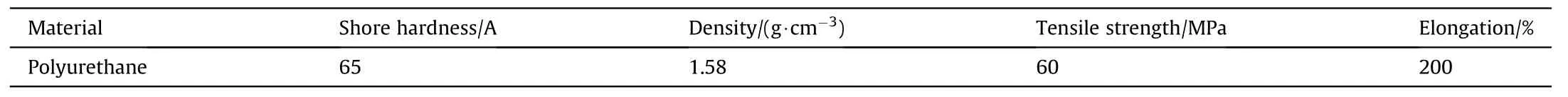
Table 3Performance parameters of the Polyurethane.
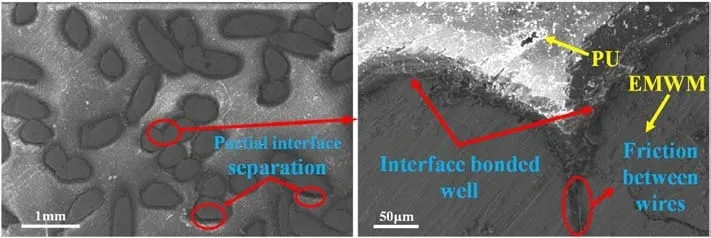
Fig.5. SEM image of the EMWM-PU composites.

Table 4Mass ratio of the EMWM-PU composites.

Fig.6. Depiction of the test system and the test tooling.

Table 5Test conditions for the mechanical properties of the materials under consideration.
A dynamic test for the composites coating structure was designed in order to explore the damping energy dissipation and stiffness characteristics of the EMWM-PU composites by using dynamic and static universal material testing equipment (SDS-200).The employed test system and the respective tooling are illustrated in Fig.6.It is noticed that there is a design gap of 5 mm between the upper and the lower cladding rings.Additionally, the pretension of the composites specimen in the EMWM-PU cladding structure can be adjusted by tuning the distance of the upper and lower cladding rings by locking the bolts.Before performing the test, the required preload distance can be set according to the specific requirements.Notably, the horizontal degree of the test fixture must be ensured and the upper chuck of the static and dynamic testing machine must be strictly centered for eliminating the influence of the axial force.Moreover,the test was initially run for 500 cycles at each frequency in order to make stabilize the specimen and acquire reliable data afterward.The detailed test conditions for the mechanical properties of the materials are listed in Table 5.In addition, the mechanical experiments were carried out at least three times and the average value was calculated.
3.2.Parameter identification
The EMWM-PU composites material exhibits nonlinear hysteresis characteristics that are directly associated with the forcedisplacement curve and the energy dissipation under enforcing dynamic loading conditions.We have to underline that the hysteresis loop area represents the energy dissipation capacity of the material.Herein,a sinusoidal displacement excitation method was used, whereas the force signal was collected by the force sensor.The maximum elastic potential energyWand energy consumption ΔWwithin a period, are illustrated in Fig.7.
The sinusoidal displacement was applied to the EMWM-PU composites by using a dynamic and static testing machine.The displacement excitation is given by the following equation:
whereX0is the amplitude of the displacement, ω is the loading period, and α is the initial loading phase.
The area of the measured hysteresis loops ΔWis calculated as follows:
where the number of the sampling points isN=f0/fin each loading vibration period,fis the maximum loading frequency,while the sampling frequencyf0is set as 5000 Hz during the execution of the dynamic test.
A good symmetry was obtained in the hysteresis loop,whereas the maximum elastic potential energyWof the EMWM-PU composites in a cycle was calculated by the following equation [47]:
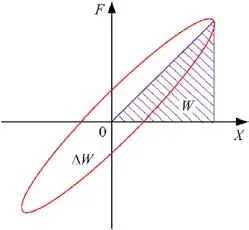
Fig.7. Restoring force-displacement curve of the EMWM-PU composites.
where,=(Fmax-Fmin)/2 is the dynamic average stiffness,whileFmaxandFminare the maximum and minimum values of the restoring force collected in the sampling system,respectively.
Finally, the loss factor of material was calculated using Eq.(3)and Eq.(4).
4.Results and discussion
4.1.Principle of energy consumption of the EMWM-PU composites
Before analyzing the results of the dynamic test, it is necessary to understand the energy consumption form of the EMWM-PU composites.As it is depicted in Fig.8, there are primarily three kinds of energy consumption phenomena that take place within the composites materials: (i) friction between the wires in the continuum EMWM, (ii) interface friction between wires and PU,and(iii)friction energy consumption between the molecular chains in the reinforced PU.On top of that, there are also four relative states between the wires in the EMWM structure,namely(a)noncontact, (b) slip, (c) stick, and (d) cross.For the EMWM-PU composites, the reinforcing PU element is filled into the internal space pores of the EMWM.Hence, there is no non-contact state in the EMWM-PU composites, but still, there are the states of slip, stick,and cross in the composites.According to the literature [48,49],there are few non-contact states of the EMWM, while the contact states of its internal wires are mainly in slipping contact and in extrusion adhesive contact.Thus, there is still a large amount of friction between the wires in the composites.When the external compression of the composites increases, the extrusion friction between the wires in contact also rises.At the same time, the interfacial friction between the host matrix EMWM and the reinforced PU also varies accordingly.Therefore,both the damping and energy dissipation characteristics of the composites also change.Interestingly, the contact friction behavior between the wires themselves and between wires and the PU can also dissipate the external vibration energy by converting the mechanical energy into thermal energy.Thus, the energy consumption of vibration is reduced.Moreover, when the polymer chains in the PU materials are subjected to external forces, the phenomena of motion and extrusion occur between the molecular chains, which could also contribute to energy loss [50].
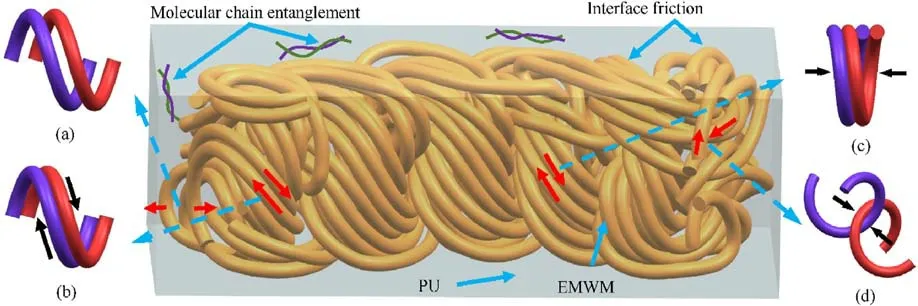
Fig.8. Internal friction of the EMWM-PU composites:(a) Non-contact; (b) Slip; (c) Stick; (d) Cross.
4.2.Dynamic properties of the EMWM-PU composites
In order to evaluate the reliability of the EMWM-PU composites and assess their capability of being used as high damping materials in hysteretic dampers,it is quite important to understand how the density [51-53], the vibration amplitude [54,55], the preload distance[56]and the frequency[57,58]affect the damping capacity of the EMWM-PU composites with different corresponding density.Furthermore, since the EMWM-PU composites are composed of both EMWM and PU, the former is associated with the density(porosity).Additionally, the amplitude, preload distance, and frequency that are the main factors affecting the damping capacity of the EMWM and PU.
4.2.1.Impact of density of the EMWM on the dynamic properties of the sample
As the continuum of the composites, the complexity of the disordered spatial network structure within the EMWM affects the mechanical properties of the materials.Along these lines, in this section, the influence of the EMWM's density (porosity) on the energy dissipation characteristics of the composites materials was systematically studied,whereas the associated hysteresis loops are divulged in Fig.9.
More specifically, as can be ascertained from Fig.9, the hysteresis loops of both EMWM and EMWM-PU composites increased as the density of the material became bigger, signifying an enhancement in the energy consumption of the material.At the same time,the extracted graph illustrates that the restoring force of the material has been also increased,i.e.the average stiffness of the material enhanced as the density increased.Furthermore, the acquired hysteresis loop area and restoring force of the EMWM-PU were significantly larger than that of the pure EMWM and PU under the same density of EMWM.This outcome clearly demonstrates that the prepared EMWM-PU exhibits better energy dissipation and stiffness characteristics.Moreover, in order to quantitatively study the energy consumption and the stiffness characteristics of the different materials, the loss factor, energy consumption, and average stiffness of the materials under consideration were calculated by using Eq.(3)-Eq.(5) and the changing pattern that is disclosed in Fig.10.
The loss factor of the EMWM decreased with the rise in density,while the energy consumption and the average stiffness increased(see Fig.10).Consequently, the increase in the EMWM density led to the rise in the contact points between wires.Hence, the energy consumption of the EMWM increased.However,the restoring force required for the EMWM compression to a certain amplitude is also enhanced with the increase of the density.This phenomenon induced a maximum elastic potential energy growth rate of the EMWM greater than that of the energy consumption.Thus,the loss factor decreased with the increase in density.
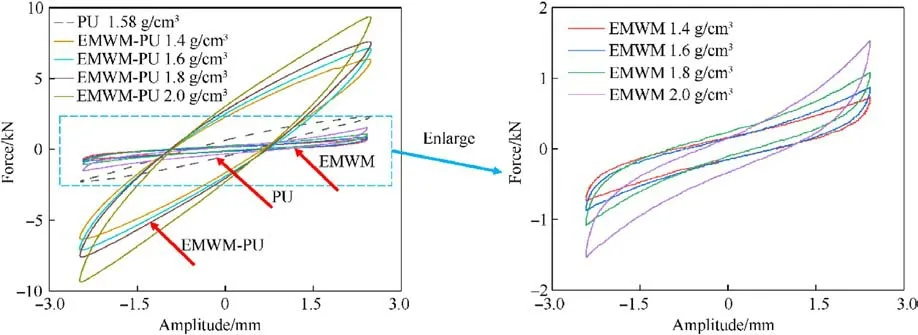
Fig.9. Hysteresis loops of the samples with different EMWM density (The mass ratios of the EMWM-PU were 51.15%, 54.54%, 58.44%, and 60.70%, amplitude: 2.5 mm, preload:1.0 mm, and frequency: 2 Hz).
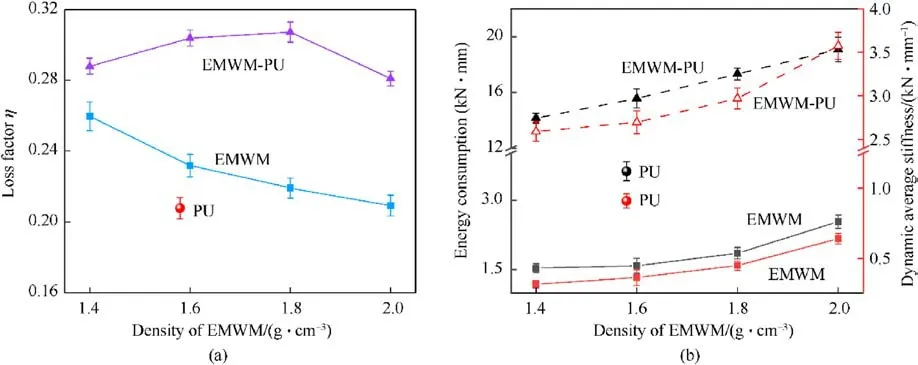
Fig.10. Impact of the density of the EMWM on the dynamic properties: (a) Loss factor; (b) Energy consumption and dynamic average stiffness.
We have to underline that the loss factor, energy consumption,and average stiffness of the EMWM-PU composites were significantly higher than those of both pure EMWM and PU.The main reason for this phenomenon is that the loss factor of the EMWM-PU composites consists of three parts (see Fig.8 and Fig.11), namely the friction damping between the continuum wires, the polymer damping within the PU, and the interfacial friction damping between the wires and the PU.As the density of the EMWM increases,both the contact interface between the wires and the PU and the friction between the wires in the composites material increase.Therefore, the loss factor, energy consumption, and average stiffness of the composite material are enhanced.However, with the continuous rise in the density of the EMWM in the composites,the loss factor between the wires decreases (as it is depicted in Fig.10(a))until the reduction of the loss factor between the wires is greater than the interfacial friction energy consumption between the wires and the polyurethane.As a consequence,the loss factor of the EMWM-PU composites increased first,then remained relatively stable, and finally, displayed a decreasing trend, while the energy consumption and the average stiffness continued to enhance remarkably.
4.2.2.Influence of the amplitude on the dynamic properties of the sample
In this section, we have investigated the mechanical properties of the various material (EMWM-PU1.6, EMWM 1.6, and PU) with the applied amplitudes at a fixed cycling frequency of 2 Hz and got the hysteresis loops that are presented in Fig.12.The restoring forces of all the three damping materials displayed an increasing trend,whereas the relationship between the displacement and the load was nonlinear.Moreover,the restoring force and the hysteresis loop of the EMWM-PU composites materials were significantly greater than those of both EMWM and PU, signifying that the EMWM-PU composites possesses better energy dissipation and stiffness characteristics under the same amplitude.
Fig.13 illustrates the variation of the mechanical properties of the different materials as a function of the amplitude.As can be observed, by increasing the loading amplitude, the energy consumption of the EMWM continuously increased, while the loss factor decreased sharply.The underlying reason for this effect is that the slip mechanism of the internal wires of the EMWM damping specimen became more difficult since the dry friction increased with the rise in amplitude[23].Thus,an elevated energy consumption took place.However, the increasing pattern of the material's maximum elastic potential energy was smaller than the respective increasing trend of the energy consumption.Hence,the EMWM loss factor decreased gradually.It is noticed that PU is a viscoelastic polymer that is composed of long-chain molecules with simple chain segments.As a result,when it is subjected to an external force,the distortion of the internal molecular chain of the PU delays behind the change of the external load, thus forming a phase difference and generating vibrational energy consumption.Therefore,the energy consumption and the average stiffness of the PU increase simultaneously with the rise in the amplitude.
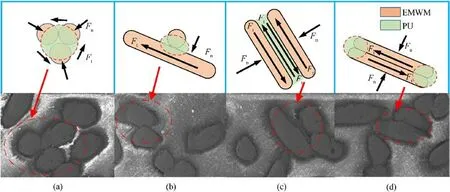
Fig.11. Friction form between wires and PU in composites.
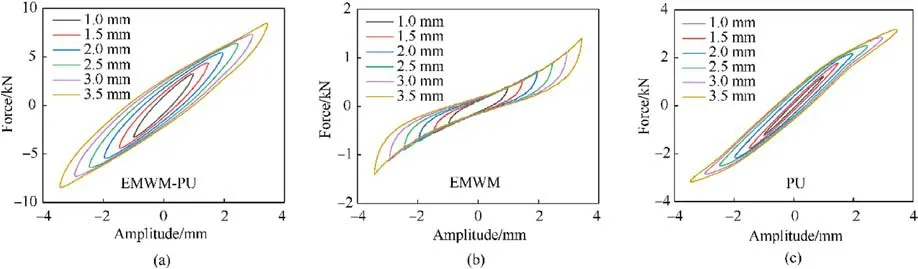
Fig.12. Hysteresis loops of the samples under different amplitudes (density of EMWM:1.6 g/cm3, preload:1.0 mm, frequency: 2 Hz): (a) EMWM-PU; (b) EMWM; (c) PU.
As far as the EMWM-PU composites is concerned, the friction between the wires increased with rising in amplitude,whereas the interfacial friction between the wires and the PU was also amplified.Thus, the loss factor and the energy consumption increased sharply.However, with the continuous increase in the amplitude,the loss factor of both EMWM and PU in the composites decreased,while the enhancement in the interfacial friction damping could no longer offset the damping reduction of both EMWM and PU.As a result, the loss factor decreased.Meanwhile, as it is illustrated in Fig.13(a),the EMWM possesses a higher loss factor at small loading displacement.More specifically, as the loading displacement increased, the loss factor of the EMWM decreased sharply from 0.331 to 0.185,which is a reduction of 44%.On top of that,the loss factor of the EMWM composites remained above 0.26, which remained at a high level.As it is divulged in Fig.13(b), when the loading amplitude increased from 1 to 3.5 mm,the average stiffness of the EMWM-PU composites decreased slightly.By enforcing a further increase in the amplitude, the energy consumption amplified sharply from 2.70 to 26.50 kN mm,which is an increase of 9.8 times.The above effect indicates that the prepared EMWM-PU composites material exhibits great energy consumption and stiffness characteristics under the application of different loading amplitudes.At the same time,it is noted that the proposed EMWM-PU composites have variable stiffness characteristics similar to EMWM, while they exhibit obvious linear elastic stage, soft characteristic deformation stage, and exponential hardening stage under the enforcement of different loading displacement [59].
4.2.3.Impact of the preload distance on the dynamic properties of the sample
In this section, the influence of the preload distance on the dynamic properties of the sample was thoroughly studied and the EMWM-PU1.6 (mass ratio: 54.54%) was selected.The extracted hysteresis loop is revealed in Fig.14.The change of the preload distance signifies the change of the pre-compression between the wires and between the wires and the PU within the EMWM-PU composites material, which has a great impact on the damping energy consumption and stiffness of the composite material.Additionally, the hysteresis area of the three damping materials increased with the reduction of the pretension distance,indicating that the absolute energy dissipation capacity of the material has been enhanced.The required restoring force also increased as the pre-tightening distance decreased, which indicates a rise in the average stiffness of the materials.
Fig.15 reveals the decrease in the loss factor, energy consumption, and dynamic stiffness, whereas the decreasing trend of both EMWM-PU and PU are prominent.Moreover, the increase in the pre-tightening distance is equivalent to the decrease in the precompression between the molecules inside the PU.Therefore, the loss factor, energy consumption, and average stiffness of the PU declined with the rise in the preload distance.Similarly, the manifestation of a larger pretension distance signifies a smaller pre-compression distribution between the wire and the polyurethane within the EMWM-PU composites.As a result, smaller interface friction at the same frequency and loading amplitude is observed.Furthermore, the dry friction (slip, stick, and cross) between the wires in the matrix material also decreases.Thus, the loss factor, energy consumption, and average stiffness of the EMWM-PU composites were reduced under the application of the external load.Meanwhile, as can be ascertained from Fig.15, the damping energy consumption and stiffness characteristics of the EMWM-PU composites materials are obviously higher than those of both EMWM and PU under the application of different preload spacing.
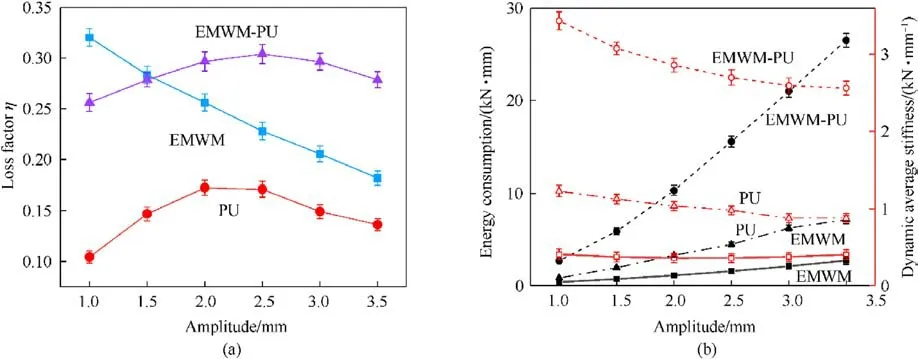
Fig.13. Impact of the amplitude on the dynamic properties, namely (a) loss factor, (b) energy consumption and dynamic average stiffness.
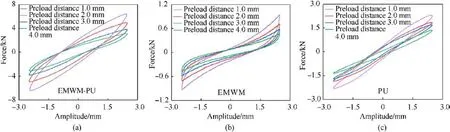
Fig.14. Hysteresis loops of samples under the application of different preload distance (density of EMWM: 1.6 g/cm3, amplitude: 2.5 mm, frequency: 2 Hz): (a) EMWM-PU; (b)EMWM; (c) PU.
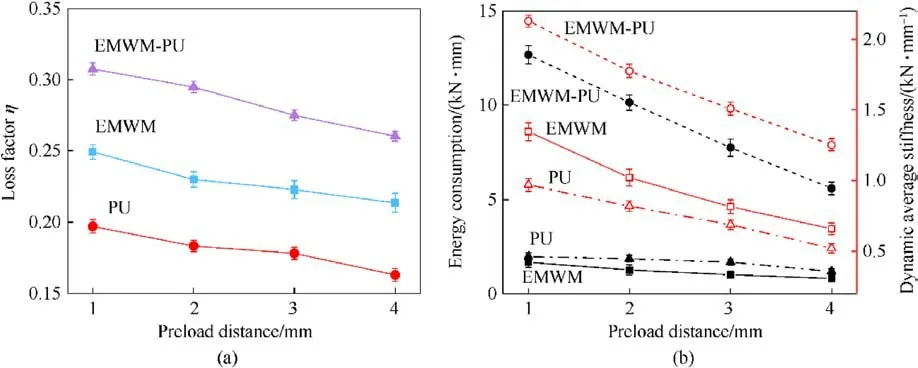
Fig.15. Impact of the preload distance on the dynamic properties, namely (a) loss factor, (b) energy consumption and dynamic average stiffness.
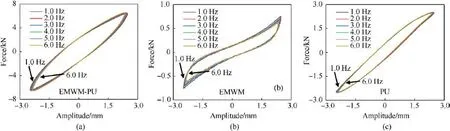
Fig.16. Hysteresis loops of the samples under the application of different frequency values(density of EMWM:1.6 g/cm3,amplitude:2.5 mm,and preload:1.0 mm):(a)EMWM-PU;(b) EMWM; (c) PU.
4.2.4.Influence of the excitation frequency on the dynamic properties of the sample
In order to explore the stability of the EMWM-PU composites under the enforcement of different excitation frequencies, the specimens were cycled at different frequencies in the range of 1-6 Hz,whereas the variation trend of the mechanical properties of the different materials as a function of the frequency is presented in Fig.16.
As it is disclosed in Fig.16, the loss factors of the different materials did not change significantly under the application of different excitation frequencies.This effect is attributed to the rubber material that exhibits good stability in the low-frequency range at room temperature [60].As far as the EMWM material configurations are concerned, the friction velocity between the wires increased as the excitation frequency enhanced, imposing thus an elevated amount of deformation on the spiral coil.Hence,the loss factor was increased but the observed increasing pattern was not significant.As it is illustrated in Fig.17,with the rise of the excitation frequency, the energy dissipation of the EMWM-PU compound almost remained unchanged, while the average stiffness increased slightly.The main reason for the effect is that the PU was filled into the pores of EMWM.Thus,the composite consists of a relatively stable porous interpenetrating network structure.Moreover, under external excitation, the slip of the metal wire is obviously limited, which improves the internal stability of the material.Therefore, the loss factor of the EMWM-PU composites material did not change significantly.From this result,we can draw also the conclusion that the composites have excellent stability in the low-frequency band.
4.3.Fatigue characteristics of the EMWM-PU composites
The fatigue characteristics are a prerequisite for the stable use of the materials.More specifically,when the composites are subjected to external load conditions, the friction, extrusion, and slip mechanisms occur between the internal wires.At the same time, the friction and wear effects continue to take place at the interface between the continuous EMWM and the reinforced polyurethane.With the extension of the working cycle of the damping material,the degree of wear between the internal metal wires, as well as between the wires and the PU material gradually increases,which has a profound impact on the elastic deformation, stiffness, and damping energy dissipation capacity characteristics of the composites.Therefore, in this section, the EMWM-PU 1.6 composites material with a mass ratio of 54.54% were selected for exploring the fatigue characteristics.Additionally, the hysteresis loops of different materials under the application of 200000 consecutive cycles are illustrated in Fig.18.

Fig.17. Influence of the excitation frequency on the dynamic properties.
As it is presented in Fig.18, the restoring force required by the three materials declined with the increase in the loading cycle.Furthermore, by increasing the loading period, the hysteresis loop gradually converged inward and tended to be flattened.This outcome indicates that the enhancement of the number of fatigue load cycles leads to an accumulation of the internal damage of the EMWM-PU compound.As a result,the damping energy dissipation capacity decreased, but it could still maintain a good damping energy dissipation performance.In addition, with the rise in the vibration cycles, the hysteresis loop rotated counterclockwise, and the bearing capacity elevated within a small change range, which indicates that the EMWM-PU composites maintained a good bearing capacity in the long-term fatigue life test.Fig.19 and Table 6 display the trend of the dynamic characteristics of materials with the loading cycle.
As it is illustrated in Fig.19, the energy dissipation and the stiffness characteristics of the three materials decrease by enhancing the vibration period.The damping characteristic of the EMWM compound primarily originates from friction energy consumption between the wires.After a certain period, the contact friction between the wires gradually changes from the running-in period to the stable period.As a result, the characteristics of energy dissipation and stiffness tend to become stable.However,compared with both the PU and EMWM-PU composites, the EMWM requires a longer period to enter the stable phase(140000 times as it is divulged in Fig.19(a)).More specifically, at the initial stage of the fatigue loading(as it is illustrated in Fig.19(a)for 40000 times), the state between the wire and the polyurethane phase in the EMWM-PU composites was still bonded,whereas the interface was relatively stable.By elevating the loading cycle, the internal structure of the EMWM-PU composites began to become unstable,while the interface between the wires and the PU was damaged,which led to partial debonding(as it is illustrated in Fig.20).At this stage, the contact friction between the wires, as well as the interface friction between the wires and polyurethane increases.Thereby,the decreasing trend of energy consumption and stiffness slows down,while the loss factor increases to a certain extent.Such a phenomenon is ascribed to the damping enhancement caused by the fatigue damage[61].As can be ascertained from Fig.20,the host matrix and the reinforcement element were not fully separated in the composites material after the enforcement of the cyclic fatigue loading (Fig.20(b) and Fig.20(c)).Interestingly, after 200000 cycles, there was still a large number of bonding states between the wires and the polyurethane within the composites,while the twophase interface of the composites was not destroyed completely.Besides, the macroscopic size of the EMWM-PU composites material was not changed significantly,which also divulges to a certain extent that the as-prepared composite material possesses good stability.Hence, it can be concluded that the EMWM-PU composites exhibits good stability.
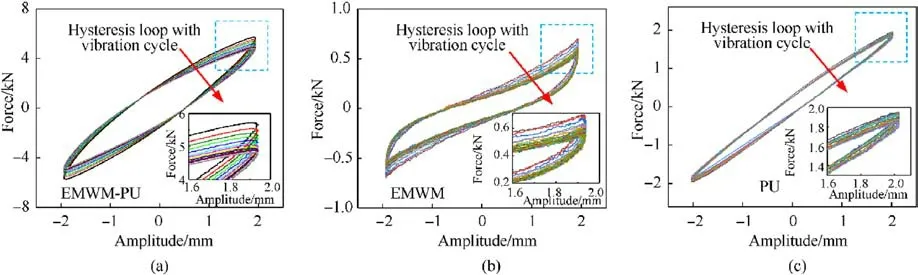
Fig.18. Hysteresis loops of the samples as a function of the vibration cycle(density of EMWM:1.6 g/cm3,amplitude:2.0 mm,preload:1.0 mm,and frequency:4 Hz):(a)EMWM-PU;(b) EMWM; (c) PU.
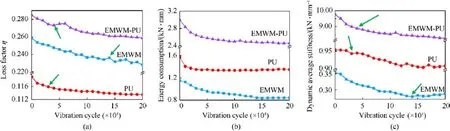
Fig.19. Dynamic characteristics of the samples as a function with the vibration cycle: (a) Loss factor; (b) Energy consumption; (c) Dynamic average stiffness.

Table 6Energy consumption and stiffness characteristics of the samples as a function of the vibration cycle.

Fig.20. SEM of the EMWM-PU composites after the application of the fatigue loading cycle.
By considering the residual stiffness decay characteristics that have been proposed for the study of the composites materials[62],the stiffness damage factorDk,and the energy damage factorDΔWwere consequently introduced in order to characterize the degree of the fatigue damage of the materials under investigation.The expression of stiffness damage factorDkcan be derived from the following equation:
whereDk(n)is the material stiffness damage factor,k0is the initial average stiffness of the test specimen andknis the average stiffness of the specimen after the application ofncyclic loads.
whereDΔW(n) is the material energy dissipation damage factor,ΔW0is the initial energy consumption of the specimen,and ΔWnis the energy consumption of the specimen after the enforcement ofncyclic loads.The employed boundary condition of the damage factor is
As it is depicted in Fig.21,the accumulation of fatigue damage of the materials imposes an increased damage factor.More specifically, PU reached the stable stage after the application of 30 000 cycles of loading,while the EMWM-PU composites attained a stable state after the enforcement of 40 000 cycles.Interestingly, the EMWM composite required about 140000 times to enter the stable period,which is 100000 cycles slower than that of the EMWM-PU composites.This result is mainly ascribed to the disordered and complex spatial network structure inside EMWM [63].Therefore,with the increase in the loading cycle,the contact form between the internal wires becomes gradually stable.When subjected to external loads, the unstable state between the metal wire and the PU in the EMWM-PU composites begins to transform,whereas the transitions from the running-in to the stable period take place in a relatively short time.Thus, the EMWM-PU composites enter the stable phase faster.Furthermore, as can be observed from Fig.21,the extracted order of damage factors is EMWM>EMWM-PU>PU.Therefore, the maximum damage factor of the EMWM-PU configuration was about 65% of the EMWM, indicating that the EMWMPU composites possesses better fatigue resistance.
5.Model establishment
The goal of this section is to develop a nonlinear constitutive dynamic model of EMWM-PU composites for predicting the influence of the various experimental parameters on the dynamic properties of the composites.According to the above-mentioned results of the dynamic test process, the restoring force hysteresis loop of the EMWM-PU composites can be decomposed into a nonlinear elastic restoring force curve and nonlinear viscous damping force curve(see Fig.22).

Fig.21. Damage factor of the samples as a function of the vibration cycle: (a) Energy damage factor and (b) stiffness damage factor.
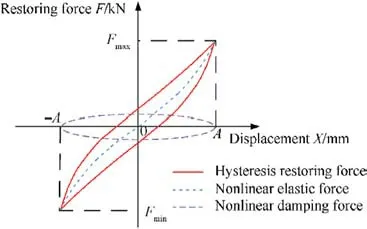
Fig.22. Exact decomposition of the hysteresis loop.
Bai et al.[64-66]concluded that the primary linear and tertiary nonlinear stiffness play a decisive role in the elastic restoring force distribution.Therefore, the nonlinear elastic restoring forceFkcan be expressed as follows:
wherek1andk3are the primary linear and tertiary nonlinear stiffness coefficients respectively, andXis the deformation of EMWM-PU composites.
As it is illustrated in Fig.22, the nonlinear damping force exhibits the shape of a nonlinear closed curve.In addition, the damping component factor was used for describing more complex nonlinear damping force and it can be expressed by the following equation:
In the equation,cand α stand for the damping coefficient and damping component factor respectively, while sgn{} is the symbolic function.
Therefore, the nonlinear dynamic model of EMWM-PU composites can be expressed as follows [67]:
The acquired dynamic experimental results demonstrate that the damping and stiffness characteristics of the EMWM-PU composites were mainly affected by the amplitude and density,whereas the frequency had a negligible impact on the dense materials.In order to further describe the connection between the hysteresis loop and the dynamic parameters, the elastic restoring force can be expressed as a functional relationship between the amplitude and density.As a result, Eq.(11) can be modified as follows:
whereAis the loaded amplitude and ρ is the density of the matrix EMWM in the composite.
5.1.Identification of the nonlinear stiffness coefficient
The test data of the composites with different densities of EMWM and different amplitudes were selected for fitting purposes in the study(preload:1 mm and frequency:1 Hz).Compared with the polynomial and the trigonometric function fitting, the power function fitting method possesses the advantages of fewer unknown variables and a simpler fitting structure.Therefore,the firstorder linear stiffness and third-order nonlinear stiffness were fitted by using the power functions that are shown in Eq.(13) and Eq.(14), while the respective fitting results are divulged in Fig.23.

Fig.23. Space surface of the nonlinear stiffness coefficient: (a) K1; (b) K3.

Table 7Results of the stiffness coefficient.
whereK1andK3are the first-order linear stiffness and the thirdorder nonlinear stiffness coefficients of the composite,respectively.
As it is illustrated in Fig.23, the stiffness coefficient gradually decreased by enhancing the amplitude,indicating that the EMWMPU composites presents soft characteristics [67].Moreover, the first-order linear stiffness change pattern was more sharply than the third-order nonlinear stiffness.Meanwhile,the variation range of the stiffness coefficient decreased gradually as the amplitude elevated, while the stiffness coefficient was enhanced with the increase in the density.The fitting results of the stiffness coefficients are listed in Table 7.
5.2.Identification of the damping coefficient and the damping component factor
According to the nonlinear functional constitutive distribution,the nonlinear damping force is equal to the actual collected total restoring force minus the nonlinear elastic restoring force, i.e.
The variation relationship of the nonlinear damping force with the density and the amplitude is quite complex.Additionally, the power series could not fit the variation law of the damping force accurately.For that reason, the polynomial fitting can effectivelysolve the problem of the fitting accuracy and achieve the best fitting effect.The space surface of the fitted damping coefficient and the damping component factor are displayed in Fig.24.

Table 8Results of the damping coefficient.

Table 9Results of the damping component factor.
As it is revealed in Fig.24, the variation trend of the damping component factor is more complex than that of the damping coefficient.After performing multiple fittings, it was found that the damping coefficient can be well fitted by Eq.(16), while the damping component factor can be fitted by Eq.(17) in order to better predict the damping performance of the composite materials.The acquired fitting results are listed in Tables 8 and 9.
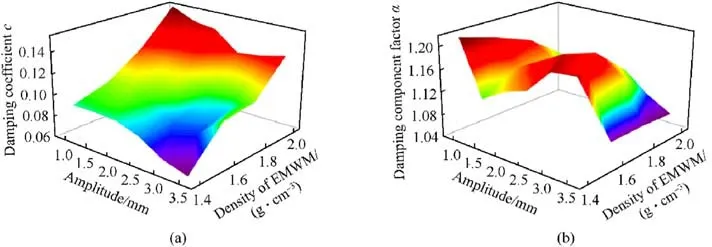
Fig.24. Space surface of the damping coefficient and damping component factor: (a) c; (b) α.
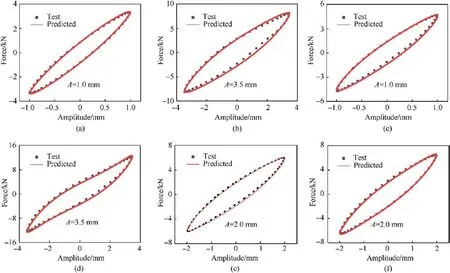
Fig.25. Prediction of amplitude-force curve of EMWM-PU composites: (a) and (b) EMWM-PU 1.4; (c) and (d) EMWM-PU 2.0; (e) EMWM-PU 1.6; (f) EMWM-PU 1.8.
The constitutive relationship model of the nonlinear functional function of the EMWM-PU composites material can be obtained by substituting the identified relational Eq.(13)-Eq.(17)into Eq.(12).
5.3.Model verification
According to the above-mentioned parameter identification,the hysteresis loop of the recovery force for the EMWM-PU composites can be re-constructed.In order to verify the accuracy of the nonlinear functional constitutive model,a comparison between the estimated curves that were fitted by the proposed model and experimentally measured results was performed.Fig.25 presents the comparison results of the hysteresis curve that are associated with the restoring force and displacement under the application of different amplitudes and densities of EMWM.
As it is illustrated in Fig.25(a)-Fig.25(f), the damping coefficient and damping component factor reflect the damping energy consumption of the EMWM-PU composites.On top of that, the extracted variation with amplitude and metal rubber density is in high consistency with the measured data.Hence, the nonlinear universal function constitutive model that was established in this study can accurately describe the variation of the displacementforce hysteresis loop of the EMWM-PU composites.
6.Conclusions
In this work, a novel entangled metallic wire materialspolyurethane (EMWM-PU) interpenetrating phase composite was prepared by injecting PU into the EMWM, with the aim of investigating the mechanical performance of the composites.A nonlinear universal function constitutive model of the EMWM-PU composites was also established.From our data, we can draw the following conclusions:
(1) The impact of the density of the EMWM,loading amplitude,preload distances, and excitation frequency on the dynamic mechanical properties of the composites was thoroughly analyzed.Owing to the introduction of interfacial friction between the PU and the wires, three forms of dry friction(slip, stick, and cross) between wires can be identified,whereas the prepared composites exhibit higher damping and stiffness characteristics.
(2) Based on the analysis of the fatigue characteristics of the composites, it can be ascertained from the changes of the macroscopic mechanical properties and microstructure that the proposed composites possess excellent fatigue resistance.The composites present a certain interface failure,while a reduction of the stiffness with the continuous loading cycles was also observed.Nevertheless,this interface failure can improve the energy dissipation characteristics of the composites a certain.
(3) The dynamic hysteresis loop of EMWM-PU composites was accurately decomposed into the elastic restoring force curve and the nonlinear viscous damping force.The nonlinear constitutive dynamic model of the composites is established by using the least square method,whereas a good agreement between the experimental and the numerical results was achieved.
Data availability statement
The data used to support the findings of this study are available from the corresponding author upon request.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
We thank National Natural Science Foundation of China (Grant No.52175162, 51805086 and 51975123); Natural Science Foundation of Fujian Province (Grant No.2019J01210); Health education joint project of Fujian Province (Grant No.2019-WJ-01).
- Defence Technology的其它文章
- A comparative single-pulse shock tube experiment and kinetic modeling study on pyrolysis of cyclohexane, methylcyclohexane and ethylcyclohexane
- Investigation on thermal characteristics and desensitization mechanism of improved step ladder-structured nitrocellulose
- 2D metal-organic frameworks endow ammonium perchlorate with enhanced thermal effect
- Thermal decomposition effect of MgCo2O4 nanosheets on ammonium perchlorate-based energetic molecular perovskites
- Modification of SDOF model for reinforced concrete beams under close-in explosion
- Air combat target maneuver trajectory prediction based on robust regularized Volterra series and adaptive ensemble online transfer learning

