Vibration attenuation of meta-mortar with spring-mass resonators

Sn-feng Liu , Hi-long Chen , Yng Liu , Hu-gung He , Xi-yue An , Feng-nin Jin ,Hu-lin Fn ,*

a State Key Laboratory for Disaster Prevention & Mitigation of Explosion & Impact, Army Engineering University of PLA, Nanjing, 210007, China

b Research Center of Lightweight Structures and Intelligent Manufacturing, State Key Laboratory of Mechanics and Control of Mechanical Structures,Nanjing University of Aeronautics and Astronautics, Nanjing, 210016, China

Keywords:Meta-mortar Vibration attenuation Spring-mass resonators

ABSTRACT Metamaterial based on local resonance has excellent vibration attenuation ability in low frequency.In this research,an attempt was performed to make meta-mortar with spring-mass resonators to attenuate vibration and shock hazards.Single-spring-mass resonators and dual-spring-mass resonators were designed and made using lead or aluminum blocks and SWPB springs encased by PMMA (polymethyl methacrylate) or aluminum frames.These resonators were placed into mortar blocks to make metamortar specimens.Vibration attenuation effect was investigated by sweeping vibration with frequency from 50 Hz to 2000 Hz.All these meta-mortar blocks exhibit excellent vibration attenuation ability in the designed band gaps.With dual-spring-mass resonators, meta-mortar blocks have two distinct vibration attenuation bands.

1.Introduction

In 2000, Liu et al.[1]proposed a metamaterial based on local resonance to form band gaps by periodically inlaying metal balls wrapped by rubber material into resin matrix.Local resonance greatly expands the application of metamaterials in the area of low frequency,therefore,it has attracted attentions of many researchers[2-4].For instance, Nobrega et al.[5]investigated band gaps of metamaterial rods by two numerical methods.Xiao et al.[6,7]made metamaterial beams and plates with local spring-mass structures and studied the formation mechanism of band gaps.Hasan et al.[8]developed a new approach to model and quantify the stop band.Liu et al.[9]studied the transmission loss of a cylindrical shell mounted with local resonators.Yu et al.[10]proposed a theory to describe flexural wave propagation in periodic structures on elastic foundations.Miranda et al.[11-13]analyzed flexural wave band gaps in a Timoshenko beam with multiple periodic arrays of resonators.It is clear that the local mass and the coating layer are the key components of local resonant metamaterials, which jointly determine the band gaps of the metamaterial[14-16].Spring-mass resonator is one of the simplest local resonant structures for local resonant metamaterials [17,18].

The concept of metaconcrete was proposed by Mitchell et al.[19].Inclusions with soft coatings were periodically embedded in concrete to form metaconcrete.Mitchell et al.[20]investigated the effect of different fracture parameters on the performance of the metaconcrete slab under shock loading, while Muhammad et al.[21]presented a comprehensive numerical simulation study.Liu et al.[22]studied the vibration attenuation performance of metaconcrete with double-mass-coating resonators, which has more excellent vibration attenuation ability.Li et al.[23]designed a rubber concrete beam and experimentally investigated the vibration attenuation.Briccola et al.[24,25]designed metaconcrete with different types and distribution forms of resonant inclusions.These studies reveal that when the frequency of the dynamic load is close to the local resonant frequency of the resonator, the resonance of the resonator can greatly dissipate the input energy and attenuate the wave propagation.

Some scholars [26-30]tried to use the metaconcrete to attenuate the explosion effect.Gao et al.[26]investigated the wave attenuation effect of metaconcrete slabs.Xu et al.[27-29]studied band gaps in metaconcrete with various configurations of engineered aggregates and the influences of geometric and material parameters of engineered aggregates on the band gap.Metaconcrete has superior wave attenuation performance than plain mortar under various loading.Kettenbeil and Ravichandran [30]completed experimental researches.Compared with homogeneous epoxy specimens, the reduction of the maximum strain in metaconcrete is up to 72%.It is clear that metaconcrete has excellent vibration and wave attenuation ability.

Usually, the local resonator is rubber-wrapped and concrete strength reduction by the resonator is seldom considered.In this research, two types of spring-mass resonators made of metallic masses and steel springs were designed, made and placed into mortar to construct two types of meta-mortar.One contains singlespring-mass resonators and the other has dual-spring-mass resonators.Vibration attenuation effectof meta-mortar blocks were investigated through sweeping vibration with frequency from 50 Hz to 2000 Hz, which can provide reference for vibration attenuation in concrete structures.Quasi-static mechanical properties of meta-mortar were also studied.

2.Vibration attenuation mechanism of local resonance metamaterial

2.1.Metamaterial with single-spring-mass resonators

The spring-mass resonator can realize negative effective mass based on the local resonant mechanism.Many scholars have studied the equivalent negative mass theoretically [22,30,31].According to Tan at al.[32],as shown in Fig.1(a),the effective mass of metamaterial with single-spring-mass resonator,meff, is given by

wheremst=m1+m2, θ=m2/m1and.m1andm2represent the mass of the frame and the mass of the lead block in one resonator.mstis the total mass of the resonator.k2denotes the spring stiffness.θ is the mass ratio of the lead block to the frame.w2is the local resonance frequency of the resonator,andwis the input vibration frequency.Obviously, θ has great influence onmeff.The relation betweenmeff/mstandw/w2varying with θ is shown in Fig.1(b).Asw/w2→1, there is a band gap and the effective mass will be negative.The band gap becomes wider when increasing θ.w2also has a great influence on the band gap.When the effective mass is negative(meff/mst＜0),the range of the vibration frequency could be estimated by.When the mass of the frame is the same with the lead block (θ = 1) and the resonance frequency,w2, is 500 Hz, the band gap is between 500 Hz and 707 Hz.Ifw2= 1500 Hz, the band gap is between 1500 and 2121 Hz.Obviously,there is a wider band gap for the resonator with higher resonance frequency.

2.2.Metamaterial with dual-spring-mass resonators

For metamaterial with dual-spring-mass resonators, similar to the single-spring-mass resonator, as shown in Fig.2(a), the effective mass of the system is given by[24].

wheremst=m1+m2+m3andmstis the sum of the masses of the frames and lead block.andw2is the local resonance frequency of the lead block.θ1=m2/m1and θ1is the mass ratio of lead block to the first frame.θ3=m2/m3and θ3is the mass ratio of lead block to the second frame.δ1=k2/k1and δ1is the stiffness ratio of the springs.

Obviously, θ1, θ3and δ1have a great influence onmeff/mst, as shown in Fig.2(b)-2(d).The relation betweenmeff/mstandw/w2varying with θ1is shown in Fig.2(b).There are two band gaps.When increasing θ1,the band gap gets wider and the frequency of the band gap increases, especially for the second band gap.Adjusting the mass ratio of the lead block to the first frame can adjust the attenuation of high frequency vibration.The relation betweenmeff/mstandw/w2varying with θ3is shown in Fig.2(c).When increasing θ3, the frequency of the band gap is almost constant but the width of the band gap increases for both band gaps.The relation betweenmeff/mstandw/w2varying with δ1is shown in Fig.2(d).The influence of δ1is the opposite,compared with θ1.In the design of dual-spring-mass resonators, employing bigger θ1and θ3or smaller δ1can drastically increase the bandwidth.

3.Meta-bars with spring-mass resonators

3.1.Design and manufacture

Fig.1. (a) Mechanical model of metamaterial with one resonating inclusion and (b) effective mass varying with frequency.

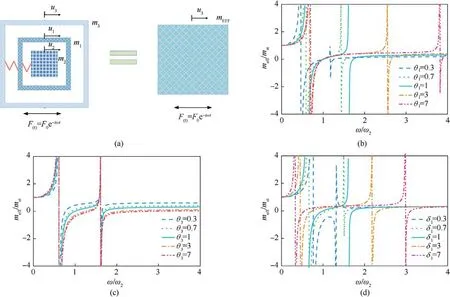
Fig.2. (a) Mechanical model of metamaterial with dual-spring-mass resonator and frequency-dependent effective mass varying with (b) θ1, (c) θ3, and (d) δ1.

Table 1Spring-mass resonator.

Three single-spring-mass resonators with frequency of 305 Hz,707 Hz and 903 Hz and three dual-spring-mass resonators with frequencies of 305 Hz + 707 Hz, 305 Hz + 903 Hz and 305 Hz+1014 Hz were designed and made,as listed in Table 1.“S”represents the single-spring-mass resonator, and “B” denotes the dual-spring-mass resonator.The dimension of the lead block is 0.014×0.014×0.008 m3.The density is 11,300 kg/m3.The mass of the lead block is 0.0177 kg.Spring is made of SWPB, which is a piano wire and used for high stress spring.The density of the PMMA (polymethyl methacrylate)frame is 1190 kg/m3.

The dimension of one single-spring-mass resonator is 0.024 × 0.024 × 0.025 m3.The mass of PMMA frame is 5.3 g, and the mass ratio between the lead block and the PMMA frame is 3.32:1.The dimension of one dual-spring-mass resonator is 0.024 × 0.032 × 0.038 m3.The mass of PMMA frame is 9.6 g, and the mass ratio between the lead block and the PMMA frame is 1.94:1.The maximum vibration amplitude of the spring is 4 mm in all resonators.Liu et al.[22]and.Tan et al.[32]indicated that 3 resonators could attenuate about 65.6%of the vibration energy and 10 resonators could attenuate almost all the vibration energy.In this research, meta-bars are connected by 5 or 10 spring-mass resonators.The key parameters of the meta-bars are listed in Table 2.“ω3N5”represents meta-bars made up of 5 single-springmass resonators with frequency of 305 Hz.“Hω3+7N10”represents meta-bars made up of two kinds of single-spring-mass resonators with frequencies of 305 Hz and 707 Hz,and the resonator number is 10 in all.“Bω3+10N5” represents meta-bars made up of 5 dualspring-mass resonators with frequencies of 305 Hz and 1014 Hz.

The process of making meta-bars is displayed in Fig.3.All the springs, lead blocks, PMMA frames and steel frames were customized from factories.PMMA frame was joined together with strong glues and the steel frame was formed by spot welding.To make the meta-bar, firstly, the spring and the lead block were bonded with epoxy resin glue to form the resonator after solidification for 30 min.Secondly, the resonator was bonded with the inside surface of the frame.The center points of all the resonators should be in a straight line.Finally,the frame was bonded together to form the meta-bar.Three species were prepared for each type of meta-bar.

The following points shall be paid attention to in the manufacturing process:(a) Selecting high bonding strength epoxy resin glue;(b)Sanding the lead block to remove surface oxides and cleaning with alcohol before bonding; (c) Flatting the two ends of the spring;(d)Covering at least a circle of the spring and the whole surface of the lead block using glue;(e)Cleaning the PMMA frame with alcohol.

Table 2Meta-bars made up of spring-mass resonators.

Fig.3. Making process of meta-bars.

Fig.4. Vibration tests: (a) Transverse vibration and (b) axial vibration.

3.2.Vibration tests

Transverse vibration tests and axial vibration tests were performed to investigate the vibration attenuation of the meta-bars,as shown in Fig.4.A strong magnet was applied to attract the metabar.The maximum vertical tension of the magnet reaches 1500 N.Before the vibration tests,the system kept balancing under gravity and spring supports,which made the gravity has little influence on the vibration tests.

The test system includes a vibration actuator,SA-JZ001.The peak load of the exciter is 20 N.The maximum amplitude is 3 mm.The frequency range is 1 kHz-15 kHz.A signal generator,SASG030 was selected, produced by Wuxi Shiao Technology Co., LTD.The frequency range of the generator is 2 Hz-20 kHz.Power output is 30 W.The scanning time is 0.1-20 s.A dynamic signal test and analysis system, DH8302, can supply channel sampling frequency up to 1 MHz.Two acceleration sensors,PCB353B15,with sensitivity of 10 mV/g and frequency range from 1 Hz to 10 kHz,were adopted to measure the input and output acceleration data.

One acceleration sensor was fixed on the bottom of the metabar to measure the input acceleration data.The other was fixed on the top to measure the output acceleration.The meta-bars were vibrated axially and transversely, respectively.The transverse vibration was a horizontal cantilever support, as shown in Fig.4(a),and the axial vibration was a vertical column support,as shown in Fig.4(b).Sinusoidal excitation was input by the vibrator with frequency sweeping from 50 to 2000 Hz.Set the sweeping period to 20 s, the sweep rate is sufficiently slow of the test equipment to make sure that close to the steady-state response conditions.

3.3.Attenuation of meta-bars with single-spring-mass resonators

Four kinds of meta-bars were excited transversely, including“ω3N5”, “ω3N10”, “ω7N5” and “ω7N10”.Here, “ω3N5” represents meta-bars made up of five single-spring-mass resonators with frequency of 305 Hz.Ordinary PMMA bars as the ordinary structure(OS) with the same volume were tested at the same time as reference.“OS1”means a 10 cm long PMMA bar,and“OS2”means the PMMA bar is 20 cm long.The attenuation of the vibration,FRF(Frequency response function), is evaluated by

where Aoand Aeare the input and output acceleration of the metabar, respectively.The energy is evaluated by

wheremis the mass of the lead block andTis the vibration test period.

The vibration attenuation effect is revealed in Fig.5.“Ending”means the output acceleration data on the top of the meta-bar,and“Origin” means the input acceleration data on the bottom of the meta-bar.The data are listed in Table 3.

As shown in Fig.5(a), the vibration attenuation band gap of meta-bar ω3N5 is from 325 to 591 Hz, close to the designed band gap from 305 to 634 Hz.At 338 Hz, it gets the highest vibration attenuation and the FRF is-11.07 dB,with acceleration attenuation rate of 72.04% and energy attenuation rate of 92.18%.The input energy is almost completely blocked and can no longer propagate in the meta-bar.

As shown in Fig.5(b), the vibration attenuation band gap of meta-bar ω3N10 is between 327 Hz and 535 Hz,which is less than the designed frequency about 100 Hz.At 343 Hz, the FRF is -18.60 dB.The acceleration attenuation rate is 88.25% and the energy attenuation rate is 98.62%.

As shown in Fig.5(c), the vibration attenuation band gap of meta-bar ω7N5 is between 764 Hz and 1226 Hz.At 808 Hz,the FRF is -12.21 dB.The acceleration attenuation rate is 75.48% and the energy attenuation rate is 93.99%.

As shown in Fig.5(d), the vibration attenuation band gap of meta-bar ω7N10 is from 761 to 1347 Hz.At 814 Hz, the FRF is -20.72 dB, which means the acceleration attenuation rate is 90.80% and the energy attenuation rate is 99.15%.

Fig.5(e) and (f) are the acceleration curves corresponding to Fig.5(c) and (d), which clearly reveal the acceleration attenuation effect and the band gap.It is found that the gravity has little effect on the transverse vibration of the meta-bar as the shear stiffness of the spring is large enough.The vibration and energy attenuation accurately occur within the designed frequency range.

It is found that the resonator number affects the vibration attenuation rate.For meta-bars with five resonators, the acceleration attenuation rate achieves 70%,and the energy attenuation rate reaches 90%.For meta-bars with ten resonators, the acceleration attenuation rate achieves 88%, and the energy attenuation rate reaches 98%.Increasing the number of resonators from five to ten,the vibration attenuation effect is strengthened and the input energy is almost completely consumed and can't propagate in the meta-bar at the designed frequency.

Six kinds of meta-bars were excited axially.The vibration attenuation effect and the vibration transmission are revealed in Fig.6, and the data are listed in Table 4 in details.

As shown in Fig.6(a),the band gap of meta-bar ω3N5 is between 316 Hz and 614 Hz.At 328 Hz, it gets the maximum vibration attenuation.The FRF is-8.27 dB.The acceleration attenuation rate is 61.41% and the energy attenuation rate is 85.11%.

As shown in Fig.6(b), the band gap of meta-bar ω3N10 is between 325 Hz and 647 Hz.At 370 Hz,the FRF is-15.44 dB and the attenuation rate is 83.10% for the acceleration and 97.14% for the energy.With ten resonators, the vibration attenuation is greatly strengthened.The energy in the designed frequency is almost completely consumed by the resonators.

As shown in Fig.6(c), the band gap of meta-bar ω3N20 is between 339 Hz and 570 Hz.At 366 Hz, the FRF is -19.38 dB, with attenuation rate of 89.26% for the acceleration and 98.85% for the energy.The attenuation effect of the meta-bar with twenty resonators is the same with the meta-bar with ten resonators, indicating that ten resonators is enough for vibration attenuation.

As shown in Fig.6(d), the band gap of meta-bar ω7N5 is between 769 Hz and 1191 Hz.At 818 Hz, the FRF is -12.44 dB, with attenuation rate of 76.12% for the acceleration and 94.30% for the energy.

As shown in Fig.6(e), the band gap of meta-bar ω7N10 is between 742 Hz and 1525 Hz.At 824 Hz, the FRF is -21.18 dB, with acceleration attenuation rate of 91.27%and energy attenuation rate of 99.24%.

As shown in Fig.6(f),the band gap of meta-bar ω9N5 is between 903 Hz and 1476 Hz.At 923 Hz, the FRF is -11.09 dB, with acceleration attenuation rate of 72.11% and energy attenuation rate of 92.22%.

As shown in Fig.6(g),the attenuation band of meta-bar ω9N10 is between 844 Hz and 1529 Hz.At 926 Hz,the FRF is-21.88 dB.The acceleration attenuation rate is 91.95% and the energy attenuation rate is 99.35%.

Keeping the same mass ratio, replacing the PMMA frame with the aluminum frame.The vibration attenuation data of meta-bar Lω7N5 is shown in Fig.6(h).The band gap is between 741 Hz and 1354 Hz.At 770 Hz, the FRF is -9.24 dB, which means the acceleration attenuation rate is 65.49%and the energy attenuation rate is 88.09%.The band gap and the attenuation rate of meta-bar Lω7N5 are almost the same with those of meta-bar ω7N5, indicating that vibration attenuation rate is related to the mass ratio of the lead block to the frame,not related to the frame material.

3.4.Attenuation of meta-bars with dual-spring-mass resonators

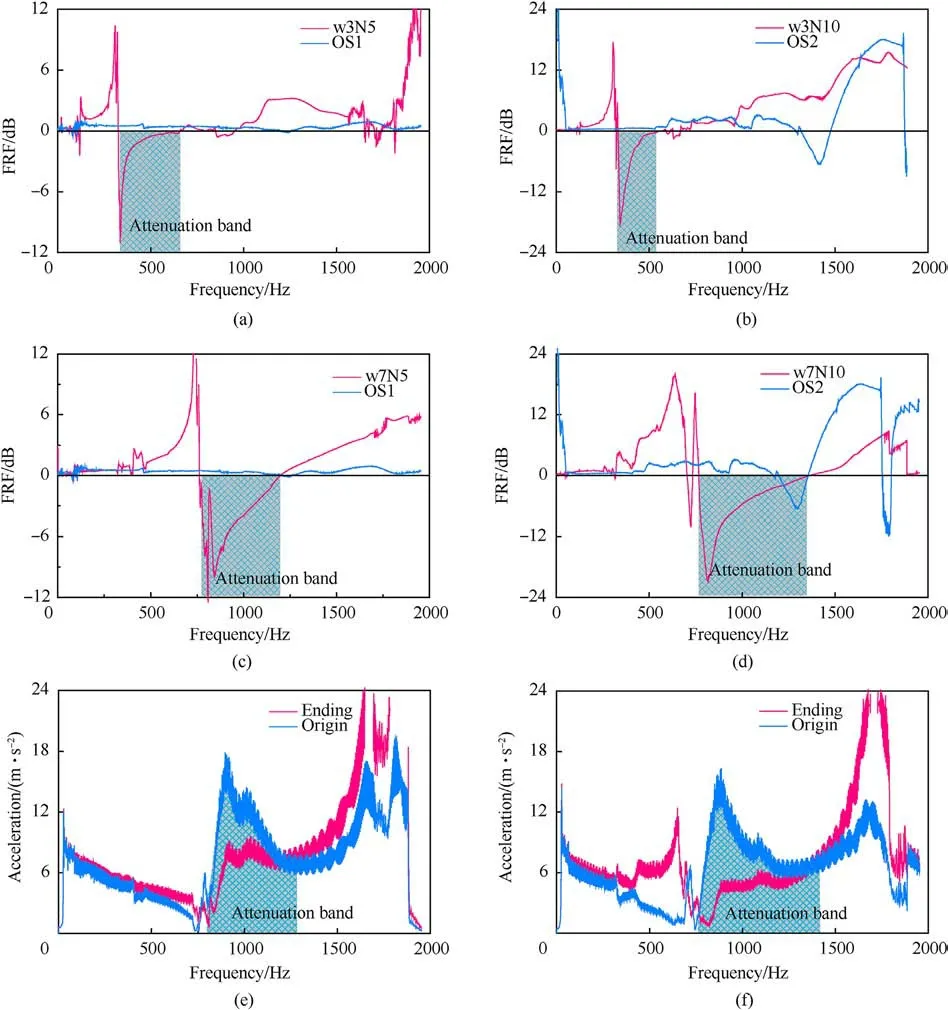
Fig.5. Band gaps in transverse vibration test: (a) ω3N5, (b) ω3N10, (c) ω7N5, (d) ω7N10, (e) Acceleration of ω7N5 and (f) Acceleration of ω7N10.

Table 3Attenuation data of meta-bars in transverse vibration test.

Meta-bars with dual-spring-mass resonators were tested axially, just as the testing of meta-bars with single-spring-mass resonators.The attenuation effect is revealed in Fig.7, and the data are listed in Table 5 in details.

Meta-bar Hω3+7N10 has two local resonant frequencies,305 Hz and 707 Hz.As shown in Fig.7(a), one of the band gap is between 389 Hz and 461 Hz.At 400 Hz,the FRF is-9.67 dB,which means the acceleration attenuation rate is 67.15% and the energy attenuation rate is 89.20%.The other band gap is between 686 Hz and 876 Hz.At 694 Hz, the FRF is -9.47 dB, which means the acceleration attenuation rate is 66.39% and the energy attenuation rate is 88.70%.

Fig.6. Band gap in axial vibration test: (a) ω3N5, (b) ω3N10, (c) ω3N20, (d) ω7N5, (e) ω7N10, (f) ω9N5, (g) ω9N10 and (h) Lω7N5.

Table 4Attenuation data of meta-bars in axial vibration test.

As shown in Fig.7(b), meta-bar Hω3+9N10 has two local resonant frequencies, 305 Hz and 903 Hz.One of the band gap is between 406 Hz and 460 Hz.At 406 Hz, the FRF is -10.18 dB, which means the acceleration attenuation rate is 69.03% and the energy attenuation rate is 90.41%.The other band gap is between 846 Hz and 958 Hz.At 907 Hz, the FRF is -9.62 dB, which means the acceleration attenuation rate is 66.96% and the energy attenuation rate is 89.09%.

Meta-bar Bω3-10N5 has five dual-spring-mass resonators, and the local resonant frequencies are 305 Hz and 1014 Hz.As shown in Fig.7(c),one of the band gap is between 265 and 463 Hz.At 271 Hz,the FRF is-9.99 dB,which means the acceleration attenuation rate is 68.34%and the energy attenuation rate is 89.98%.The other band gap is between 1021 Hz and 1076 Hz.At 1033 Hz, the FRF is -13.11 dB, which means the acceleration attenuation rate is 77.89%and the energy attenuation rate is 95.11%.The mass ratio of the second mass blockm3, to the frame of Bω3-ω10N5 is 0.60, so the second bandwidth is just about 50 Hz.

The attenuation band is related to the mass ratio of the lead block to the frame, instead of the structural material.The larger is the mass ratio, the wider is the band gap.The band gaps of metabars with dual-spring-mass resonators is reduced to 50-100 Hz in either band, due to the mutual interference of amplifications near the local resonant frequency.The acceleration and energy attenuation rate are not affected by this mutual interference.

4.Meta-mortar with spring-mass resonators

4.1.Design and production

Concrete is widely used in civil protective structures [33,34].More and more attention is paid to reduce the attenuation of vibration or shock hazards caused by earthquakes and explosions.As meta-bars with spring-mass resonators have excellent attenuation performance in local resonant frequency, they can be periodically placed into common concrete to construct metaconcrete.When the concrete is vibrated, the existence of the resonators can attenuate the vibration energy.In this research, five kinds of meta-mortar blocks were designed, made and tested, as shown in Fig.8.

Fig.7. Axial vibration test band gap of meta-bars with dual-spring-mass resonators:(a) Hω3+7N10; (b) Hω3+9N10 and (c) Bω3-10N5.

Fig.8. Meta-mortar (a) design, (b) making process and (c) vibration tests.

The dimension of the meta-bar is 0.024×0.024×0.10 m3,and the dimension of the meta-mortar with four meta-bars is 0.15 × 0.15 × 0.15 m3, as listed in Table 6.M40 represents the referenced common mortar block with the standard compressive strength of 40 MPa.Meta-mortar block Mω3N4 has four meta-bars and the local resonant frequency is 305 Hz.Meta-mortar block BMω3+ω7N4 has two kinds of meta-bars,each one have two metabars and each meta-bar has four resonators with the same local resonant frequency.One of the local resonant frequency is 305 Hz and the other is 707 Hz.Meta-mortar block BMω3+ω7N2 has one kind of meta-bar, but each meta-bar have two local resonant frequencies,305 Hz and 707 Hz,and each local resonant frequency has two resonators.

The mass ratio of the P·O42.5 cement,the medium sand and the water is 1:1.20:0.087.Added a water reducer with a concentration of 25% to the mortar with the concentration is 1%.To make the meta-mortar block, firstly, a 25 mm thick layer of mortar was poured into the mold for initial curing for 6 h.Then,four meta-bars were placing into the mold,and the mortar was poured slowly into the mold layer-by-layer and vibrated gently to densify.For each layer, the curing time is 3 h.Finally, the meta-mortar block was cured in room temperature for 28 days.

4.2.Vibration attenuation effect of meta-mortar block

Two acceleration sensors were installed above and below the meta-mortar block to measure the input and the output acceleration.The vibration attenuation effect is revealed in Fig.9, and the data are listed in Table 7 in details.

As shown in Fig.9, the FRF of the common mortar is close to zero.The common mortar block M40 has little attenuation.As shown in Fig.9(a), meta-mortar block Mω3N4 has obvious vibration attenuation effect from 352 to 654 Hz.At 386 Hz,the block gets the highest attenuation rate.The FRF is-9.78 dB,which means the acceleration attenuation rate is 67.42% and the energy attenuation rate is 89.38%.As shown in Fig.9(b),for meta-mortar block Mω7N4,the vibration attenuation band is between 668 Hz and 797 Hz.At 758 Hz, the FRF is -9.81 dB, which means the acceleration attenuation rate is 67.68% and the energy attenuation rate is 89.55%.

As shown in Fig.9(c), for meta-mortar block Mω9N4, the vibration attenuation band is between 969 and 1474 Hz.At 1004 Hz,the FRF is-7.15 dB,which means the acceleration attenuation rate is 56.10% and the energy attenuation rate is 80.72%.

As shown in Fig.9(d), with dual-spring-mass resonator,MBω3+ω7N4 has two vibration attenuation bands.One is from 284 Hz to 345 Hz.At 329 Hz, the FRF is -5.43 dB.The attenuation rate is 46.48% for the acceleration and 71.36% for the energy.The other is from 671 to 760 Hz.At 744 Hz, the FRF is -8.14 dB.The attenuation rate is 60.83%for the acceleration and is 84.65%for the energy.

As shown in Fig.9(e),for meta-mortar block MBω3+ω7N2,one vibration attenuation band is from 390 to 438 Hz.At 426 Hz, the FRF is-7.65 dB.The attenuation rate is 58.55%for the acceleration and 82.82% for the energy.The other one is between 675 Hz and 810 Hz.At 709 Hz, the FRF is -8.41 dB, which means the acceleration attenuation rate is 62.02% and the energy attenuation rate is 85.58%.

4.3.Comparisons on vibration attenuation effect

The reference mortar block M40 has slight vibration attenuation, as the acceleration attenuation rate is 11.28% and the energy attenuation rate is 21.30%.For meta-mortar blocks, the energy attenuation rate can reach 90%.The meta-mortar has much more excellent vibration attenuation.

Compared with meta-bars, the vibration attenuation effect of the meta-mortar block has a little reduction,which may be caused by that the number of resonators in each meta-bar in meta-mortar blocks is only 4.The attenuation bandwidth also reduces a little.For example, the bandwidth of meta-mortar block Mω7N4 is only 129 Hz.The bonding between the mortar and the frame changes the mass ratio and the resonation frequency.

5.Mechanical/failure properties

The meta-mortar has excellent vibration attenuation in the designed band gaps.With meta-bar resonators, the quasi-static compression strength is weakened compared with the reference mortar block, M40, whose average compressive strength is 45.42 MPa,as shown in Fig.10.

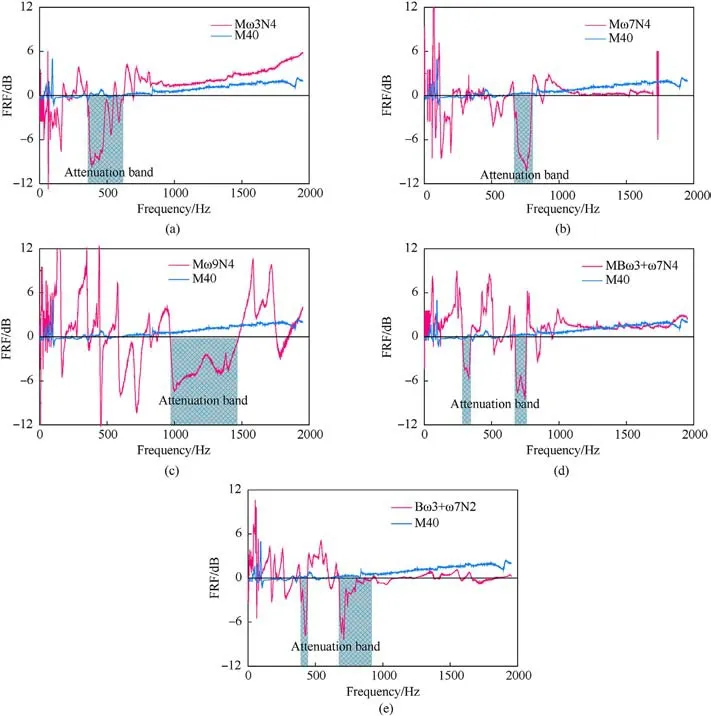
Fig.9. Vibration attenuation band of meta-mortar blocks: (a) Mω3N4; (b) Mω7N4; (c) Mω9N4; (d) MBω3+ω7N4, and (e) MBω3+ω7N2.

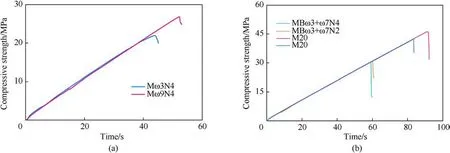
Fig.10. Strength in (a) axial compression and (b) lateral compression.

In axial compression along the axial direction of the meta-bar resonators, the compressive strength is 22.91 MPa and 27.94 MPa for Mω3N4 and Mω9N4,respectively.The reduction of the strength in lateral compression is -49.56% and -38.49% for Mω3N4 and Mω9N4,respectively.In axial direction,the area ratio of the metabars is 0.1024.The reduction is much larger than the area ratio.As the meta-bars almost penetrate the whole specimen, the stress concentration at the interface between the square meta-bars and the mortar will greatly reduce the strength with multi-cracks, as shown in Fig.11(a).If further considering the core are occupied by the meta-bars, the area ratio is 0.36, only a little smaller the strength reduction rate.

In lateral crushing, the compressive strength is 31.44 MPa and 32.14 MPa for MBω3+ω7N4 and MBω3+ω7N2, respectively.The reduction of the strength in lateral compression is -30.78%and -29.24% for MBω3+ω7N4 and MBω3+ω7N2, respectively.In lateral direction the area ratio of the meta-bars is 0.2133, but the thickness of the resonators is limited, the strength reduction is a little larger than the area ratio.The main fracture crack is located at the border between the meta-bars and the first cured mortar layer,as shown in Fig.11(b).If removing the edge layers,the area ratio is 0.320, consistent with the strength reduction rate.

Comparing the failure patterns,as shown in Fig.11(a),there are obvious vertical cracks in axially compressed meta-mortar block,because the meta-bars are vertical.As shown in Fig.11(b), cracks are inclined in laterally compressed meta-mortar block, because the meta-bars are transverse.While, there is a wide transverse crack, indicating a complete failure of block M40.

The study indicates that the existence of meta-bars changes the failure pattern of the mortar block and decreases the strength.In order to reduce the strength reduction rate,block with larger size,more uniform distribution of resonant cavity, stronger circular frame and integral concrete pouring and curing process should be adopted.

6.Conclusions

In this research, single-spring-mass resonator and dual-springmass resonator were designed, made and placed into mortar to make meta-mortar material.The vibration attenuation effect of the meta-mortar was investigated by vibration testing.Through the investigation, it can be concluded that

Table 5Attenuation data of meta-bars in axial vibration test.

Table 6Design of meta-mortar blocks with meta-bars.

Table 7Attenuation data of meta-mortar blocks.

(1) With spring-mass resonators, the meta-mortar material exhibits excellent vibration attenuation performance.The vibration attenuation band gap depends on the fundamental frequency of the spring-mass inclusion.

(2) The meta-mortar with dual-spring-mass resonators has two distinct vibration attenuation band gaps, depending on the fundamental frequencies of the two spring-mass resonators.But the bandwidth of either band is narrowed induced by the mutual interference of these two resonators.

(3) Out of the vibration attenuation band gap,the vibration will be strongly amplified.The meta-mortar is frequency sensitive and the robustness of the vibration attenuation should be improved in further research.

(4) Although spring-mass resonators endow the meta-mortar vibration attenuation ability in low frequencies, it will reduce the quasi-static compression strength of the mortar.The designing and making techniques of the meta-mortar should be further improved.

Fig.11. Failure pattern of axially compressed meta-mortar block:(a)Side view and(d)Top view;failure pattern of laterally compressed meta-mortar block:(b)Top view and(e)side view; and failure pattern of compressed M40 block: (c) Top view and (f) side view.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

Supports from National Natural Science Foundation of China(Grant No.12002160,and Grant No.11972184),China National Key Laboratory Foundation of Science and Technology on Materials under Shock and Impact (Grant No.6142902200203), Natural Science Foundation of Jiangsu Province of China (Grant No.BK20200412, BK20201286), National Defense Basic Scientific Research Program of China (TCA20030), and Science and Technology Project of Jiangsu Province of China(Grant No.BE2020716)are gratefully acknowledged.