云南省地表太阳辐射模型适用性评价及优化
孙咏琦, 李强军, 陈永志, 李建华*
(1. 云南农业大学水利学院, 昆明 650201; 2.云南农业大学自然资源科学技术工程研究中心, 昆明 650201; 3. 云南省地矿测绘院有限公司, 昆明 650218)
随着社会经济的快速发展,能源问题日益严重,传统的化石燃料不仅是不可再生能源,而且会严重破坏大气环境。一直以来太阳能、风能、潮汐能、地热能等可再生能源的研究已经成为热点[1]。地表太阳辐射是天气和气候形成的基础, 是驱动地球表层物理、化学和生物过程的根本动力[2],它是指到达地面的太阳辐射强度,而在传播过程中往往会受各地大气、纬度、海拔等因素作用从而改变辐射强度。在太阳能利用技术蓬勃发展的过程中,对日总太阳辐射数据的需求与日俱增。现阶段地表太阳辐射数据的获取通过实测以及模型估算两种方式。日射强度计通常被用于地表太阳辐射的监测,但由于其运行维护成本高[3],使得在全球范围内能观测的台站极少[4],中国至今建立了122个太阳辐射观测站,约占气象观测台站的1/12[5]。因此,利用其他气象数据建立模型计算日总太阳辐射成为中外学者广泛关注的问题之一。
多年以来,学者们提出了不同的估算方法。太阳总辐射的经验模型又根据模型中的气象因子不同分为日照时数模型、温度模型和基于多参数混合模型[6]。其中日照时数模型估算精度相对较高,基于日照百分率的计算模型为A-P模型、Ba模型等[7-11]。张佩等[12]以江苏省为例,探究不同日照情况下的太阳辐射量。于海敬[13]利用1971—2015年安徽省气象台站逐日的日照时数以及辐射数据对6种日太阳总辐射模型精度进行验证,并探究安徽省多年来太阳辐射的变化情况。童成立等[14]通过统计检验模拟结果与实际观测结果,进一步分析了中外太阳辐射模拟方法,并建立一种简单实用的模拟逐日太阳辐射的方法。目前基于温度的计算模型主要为H-S模型[15]、B-C模型等[16],这两种模型仅需日最高、最低温度就能估算太阳辐射,在对结果估算精度要求不高的领域更为实用[17]。基于多参数混合模型可以充分融合多种气象因子从而提高预测精度,朱志辉[18]提出了基于平均水汽压、海拔高度等多因子综合法全国通用模型;Chen等[19]提出的基于温度以及日照的混合模型。
中国领土面积十分辽阔,经纬跨度大,而且地形比较复杂,形态多样,不同地区不同地形地表所受到的太阳辐射有很大差异[20]。当前提出的经验模型普遍适用于中国东部平缓地区,云南地处中国西南边疆,拥有高海拔低纬度的特性导致当前的通用公式对云南省地表太阳辐射无法精确估算,而且针对同一估算模型各月的模型参数也有着较大差别,因此研究太阳总辐射模型在云南的实用性十分重要。现利用2007—2016年间云南省5个气象站(丽江、景洪、昆明、腾冲、蒙自)逐月日照百分率、气温等数据带入现有模型进行预测并与实测值进行对比,尽量减少误差从而为云南省太阳能开发利用提供帮助。
1 资料与方法
1.1 数据
云南省位于中国西南地区,地势呈西北高、东南低,自北向南呈阶梯状逐级下降,为山地高原地形,全省海拔最低的地方为76.4 m,此地与云南省最高点梅里雪山主峰卡瓦格博峰海拔相差6 663.6 m。在中国气象数据网上获取云南省5个气象站(丽江、景洪、昆明、腾冲、蒙自)2007—2016年逐月气象数据以及逐月辐射数据,包括极端最低气温、日照时数、日照百分率、极端最高气温、最大风速、最小相对湿度、平均相对湿度、平均水汽压等数据,各气象站基本信息如表1所示。
1.2 研究方法
太阳总辐射计算模型目前主要分为两大类,分别为采用晴天辐射的太阳总辐射计算方法以及采用天文辐射的太阳总辐射计算方法。本文研究中主要采用基于天文辐射的计算模型并引入多种因子对云南省太阳辐射进行估算,最终挑选出最适合计算云南省太阳辐射的模型。计算公式为
Q=f(Q0)
(1)

(2)

0.001 280sinθ+0.000 719cos2θ+
0.000 077sin2θ
(3)
σ=0.006 894-0.399 512cosθ+
0.072 057sinθ-0.006 799cos2θ+
0.000 89sin2θ-0.002 697cos3θ+
0.001 480sin3θ
(4)
式中:Q为太阳辐射;Q0为天文辐射;I0为太阳常数,取值为13.67×10-4MJ/(m2·s);T为一天的周期,s;π取值3.141 592 6;ρ为日地相对距离;ω0为日出日落角,由纬度、赤纬计算而得;φ为纬度;σ为赤纬;θ为日角。
2 过程与分析
2.1 模型因子筛选
为了探究影响云南省地表太阳辐射的因素,选取纬度、海拔、极端最低气温、平均气温、极端最高气温、平均相对湿度、平均水汽压10种因素与太阳辐射和天文辐射的比值(Q/Q0)进行相关性分析,根据图1可以得知Q/Q0与日照百分率、纬度和海拔呈现正向相关,且与日照百分率的相关性较强;Q/Q0与平均相对湿度、平均水汽压以及气温因素负相关,且与平均水汽压以及平均相对湿度等呈现较强的负相关。因此选取相关性较高且具有代表性的海拔、日照百分率、极端最低温、平均气温、极端最高温、平均相对湿度以及平均水汽压这7项作为评价指标,对云南省地表太阳辐射进行多因子估算。

表1 各气象站基本信息Table 1 Basic information of each weather station

图1 部分因子与Q/Q0的关系Fig.1 The relationship between some factors and Q/Q0
同一地点夏季正午太阳高度比较大,大气对太阳辐射削弱比较少,加之白昼长,日照时间长,到达地面的太阳辐射比较多,冬季正午太阳高度小,大气对太阳辐射削弱比较多,加之白昼短,日照时间短,到达地面的太阳辐射比较少。在一年不同季节的太阳辐射有明显差异,夏季波动较大,春季其次,秋季冬季基本平稳,短波辐射各季节不尽相同,长波辐射和净辐射夏季最高,冬季最小[21-22]。在探究地表太阳辐射估算时应严格考虑气候以及季节带来的影响,因此为了模型的估算更加精确,对选取的其各因子逐月与太阳辐射和天文辐射的比值进行相关性分析。根据表2可知在1、2、11、12月Q/Q0与这7项因子存在着明显的相关性,在其余各月Q/Q0与其中部分因子存在明显相关;日照百分率在全年与Q/Q0呈现强正相关性,海拔与Q/Q0呈现正相关的趋势,即海拔越高太阳辐射越大,这也与其他学者的研究结论基本一致[23]。
2.2 多因子综合估算模型构建
通过对各因子与Q/Q0绘制散点图(图2)可知几乎为线性关系,其中平均相对湿度、平均水汽压等与Q/Q0成负相关,日照百分率等因素与其成正相关。因此提出一种针对云南省的多因子综合估算模型(multi-factor comprehensive estimation model,MFCE),该模型将海拔、日照百分率、极端最低温、极端最高温、平均气温、平均相对湿度以及平均水汽压融合,从而可以提高模型拟合程度。该模型为
Q=Q0(a+bH+cS+dTmin+eTmean+
fTmax+gRH+hEmean)
(5)
式(5)中:H为海拔高度;S为日照百分率;Tmin为最低温;Tmax为最高温;Tmean为平均温度;RH为平均相对湿度;Emean为平均水汽压;a、b、c、d、e、f、g、h为模型经验系数。
2.3 模型精度对比验证及模拟效果分析
各月太阳辐射数据是由逐日辐射数据累加得到的,当前应用范围较广的计算模型主要分为基于日照百分率模型(S-model)以及基于温度模型(H-model),挑选出具有一定代表性的模型进行估算,计算公式如表3所示。
根据模型计算方法以及实测辐射值计算出各个公式在云南省的最适参数取值,结果如表4所示。由表4知所有模型各月参数值基于A-P模型计算的各月参数之间呈负相关关系,a几乎分布在0.20~0.30,平均为0.24,b几乎分布在0.30~0.60,平均为
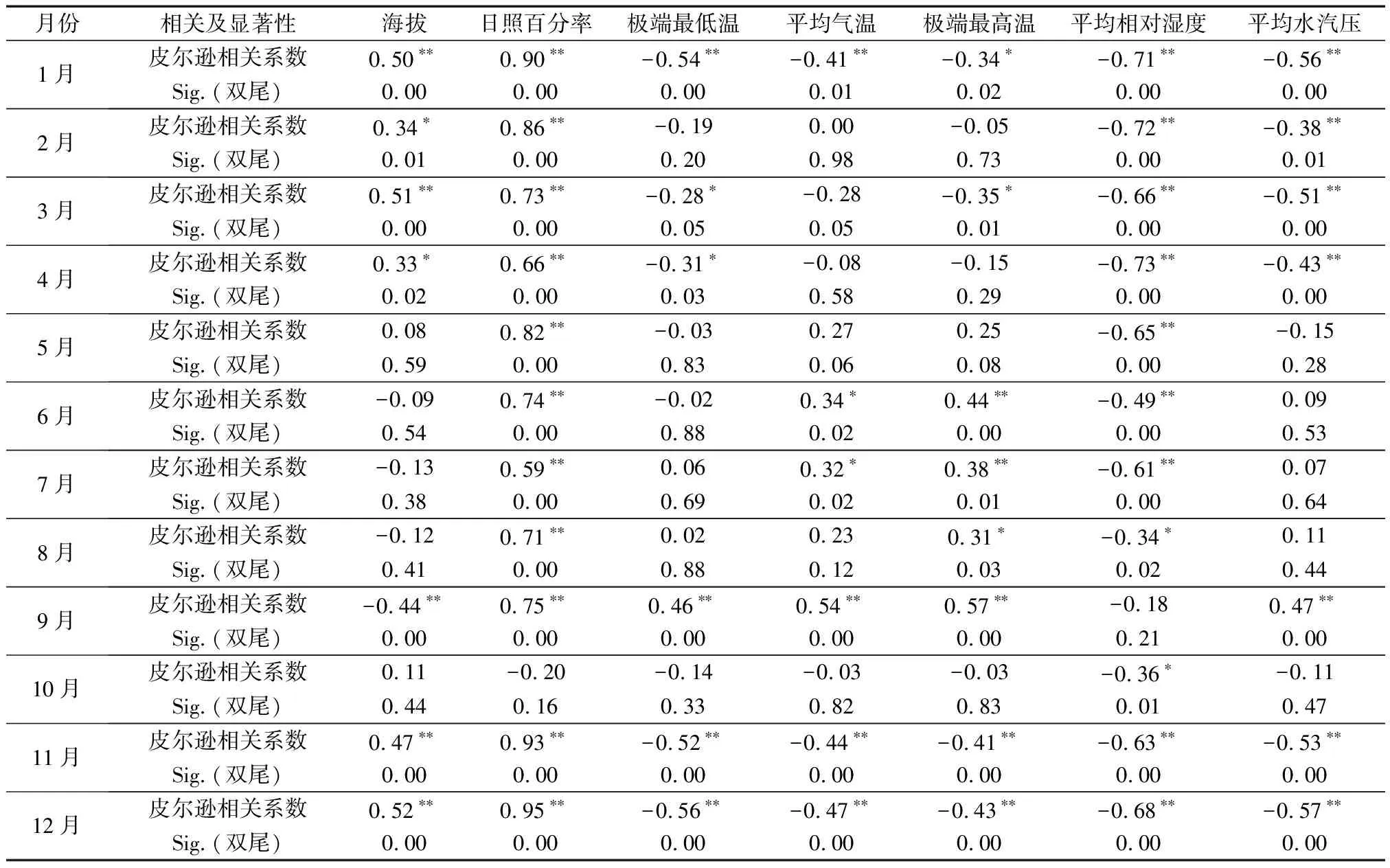
表2 各月Q/Q0与7个因子相关性Table 2 Monthly Q/Q0 was correlated with 7 factors
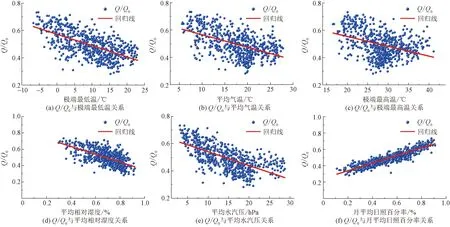
图2 Q/Q0与模型因子线性拟合图Fig.2 Linear fitting diagram of Q/Q0 and model factors
0.47。Ba模型涉及的参数中a分布在-2.00~2.00,平均为0.08,b分布在-6.00~12.00,平均值为1.24,c分布在-20~10,平均值为-1.23,d分布在-5.00~11.00,平均值为0.66;A-H模型计算的a分布在-0.05~0.10,平均为0.02,b分布在0.20~0.40,平均值为0.27;B-K模型计算的a分布在-0.70~0.70,平均为0.02,b分布在-1.50~1.60,平均值为0.07,c分布在-0.70~1.00,平均值为0.32;Fan模型计算的a分布在0~0.70,平均为0.33,b分布在-1.30~3.00,平均值为1.25,c分布在-4.20~2.70,平均值为0.93;Ab模型计算的a分布在0.30~0.60,平均为0.40,b分布在0.20~0.52,平均值为0.38,c分布在0附近,平均值为0.00,d分布在-0.34~0,平均值为-0.21。本文MFCE模型中d和f最低,证明最低温和最高温对云南省太阳辐射存影响但是相对较为微弱;g在各月的波动幅度很大,在7月份达到最大值0.66,在4月份取值最小仅为0.01,可能由于各月平均湿度存在的差异性较大;而其余参数值波动幅度小相对集中。

表3 6种不同类型太阳总辐射计算模型Table 3 Six different types of total solar radiation calculation models

表4 6种模型1—12月系数取值Table 4 Coefficient values of six models from January to December
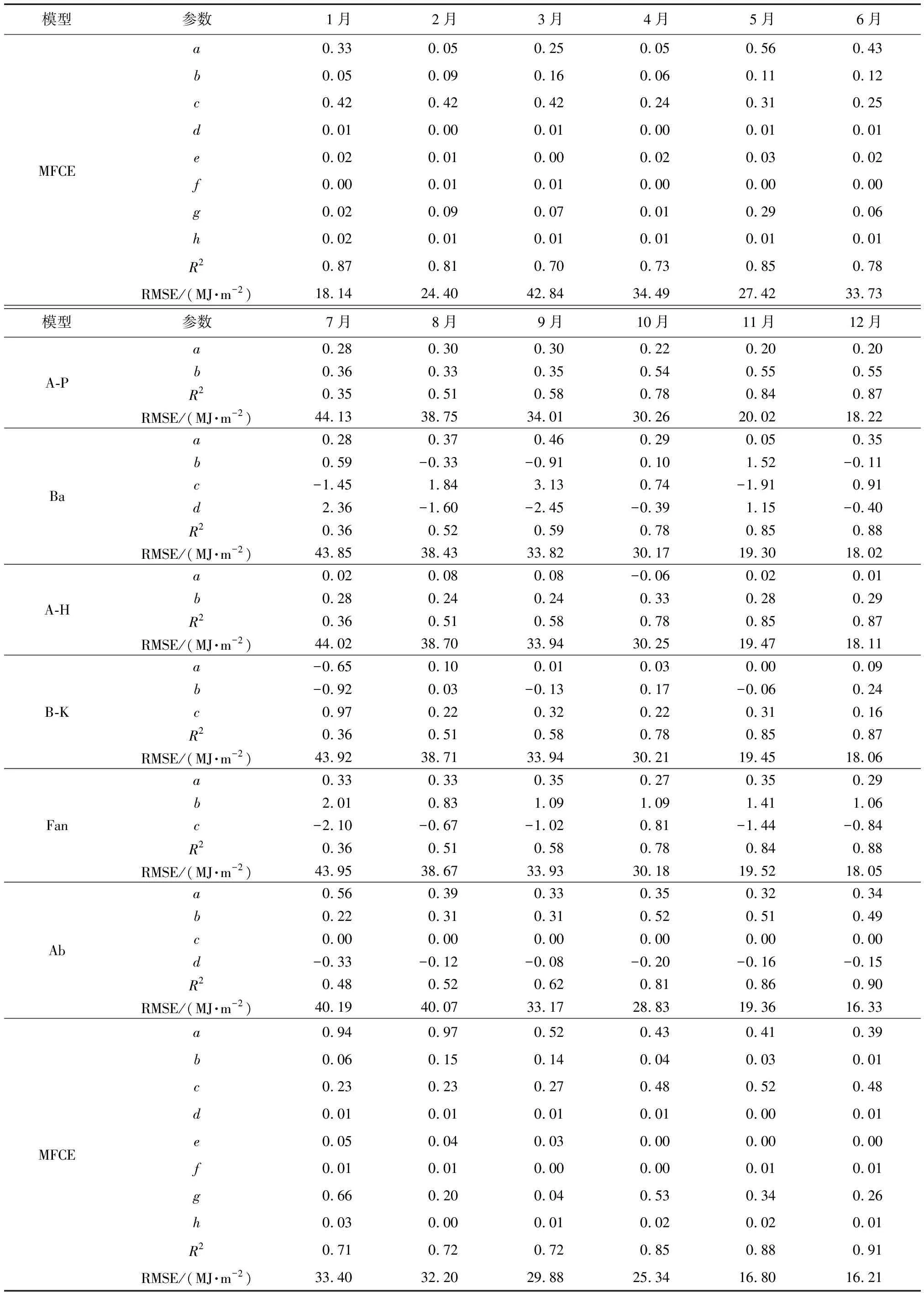
续表
采用决定性系数(coefficient of determination,R2)以及均方根误差(root mean square error,RMSE)来评价模型计算效果,R2越接近1证明模型估算值与真实值一致程度越高;RMSE越小证明模型估算值与真实值偏差越小结果越精确。在6种传统模型中预测结果最佳的为Ab模型,该模型在1月的决定性系数R2的值为0.82,比其余5种模型增加了近0.10;纵观所有模型可知,在3—9月气温较高时期各个模型对于太阳辐射的估算精度都较低,估算值与实测值的相关系数几乎未达到0.7,在7月各个模型的相关系数仅为0.4左右,且参数值和推荐值之间存在明显差异,可见依据通用方程中的推荐系数以及当前大范围的估算模型难以较为精确地估算云南地区的太阳总辐射。而MFCE模型估算值与实测值的相关系数各月均在0.7以上,最高为12月达到了0.91,且各月相关系数比其他各模型平均提高了0.3;均方根误差(RMSE)除去4月以外其余月份的值均为最小,结果分布在16.21~33.73 MJ/m2。模型精度比以往有所提高,且逐月进行模型计算,可以避免气候等自然因素对其的干扰。
3 讨论
由于当前其他学者提出的估算模型针对云南省特殊的地理条件并不适用,于是本文研究中通过因子筛选、模型构建以及精度对比验证3个部分提出了适用于云南省的基于多因子的云南省地表太阳辐射估算模型(MFCE)。利用MFCE模型对研究区5个站点太阳辐射进行估算并验证,由图3可知,估算结果与实测值整体走势基本一致,且吻合度较高,总体来说本文提出的MFCE模型在云南省的精度在可接受范围之内,且比当前其他学者提出的模型计算结果与实测值误差最小。本文提出的估算方法可为云南省光伏电站的建设及发电量的预测提供参考,也可为其他区域地表接收太阳辐射量的估算提供借鉴[28],但此方法仅适用于纬度低海拔高温差起伏大的云南省,在中国东部以及北部地区尚不适用,而中国西南省份的适用情况还有待探讨。
根据MFCE模型估算结果求各月均值,并绘制云南省太阳辐射月均值分布图(图4)。从空间分布上看,云南省地表太阳辐射值呈现西北高东南低的分布现象,这与本省海拔高度分布特点基本吻合,因此在地形起伏较大区域,地表太阳辐射量与地形关系密切。按照王国海等[29]将云南省太阳资源开发区划分的4类,可知在西北部迪庆州、怒江州、丽江市、大理州、保山市、德宏州、以及楚雄州西北部均处于最佳开发区,但由于太阳能光伏电站存在着造价高、在太阳能光伏电池板的生产过程中所付环境代价较大,因此具体最佳开发区还待进一步探究。
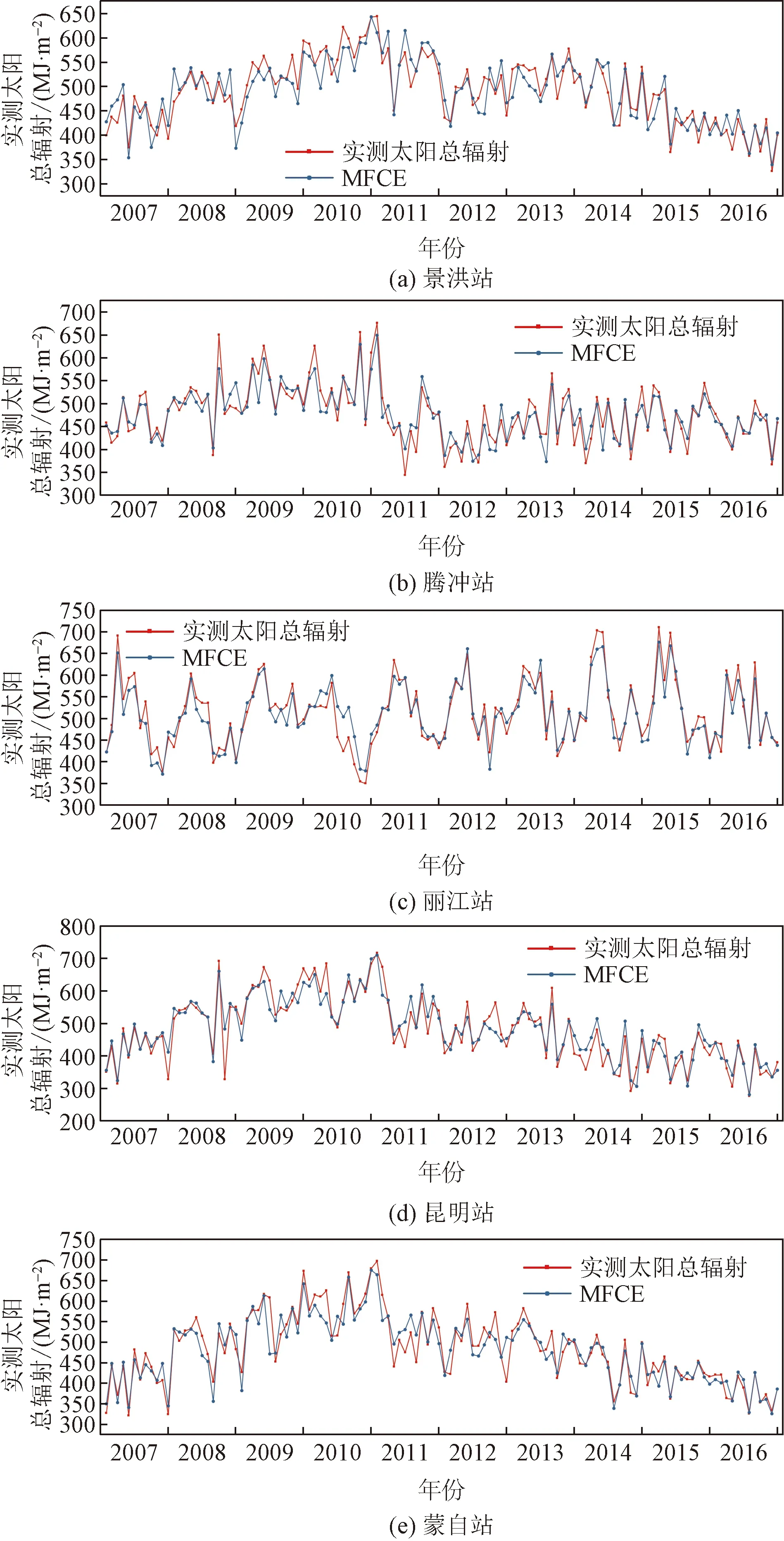
图3 站点实测值与估算值对比图Fig.3 Comparison of measured and estimated values at the site
4 结论
本文研究中提出的MFCE模型充分考虑到云南省地理位置以及气候的特殊性,以月为单位确定各月的模型系数来计算各月的太阳总辐射值。将该模型与其他模型进行对比,R2得到了明显提高,各月均在0.7以上;且均方根误差也达到了各模型中
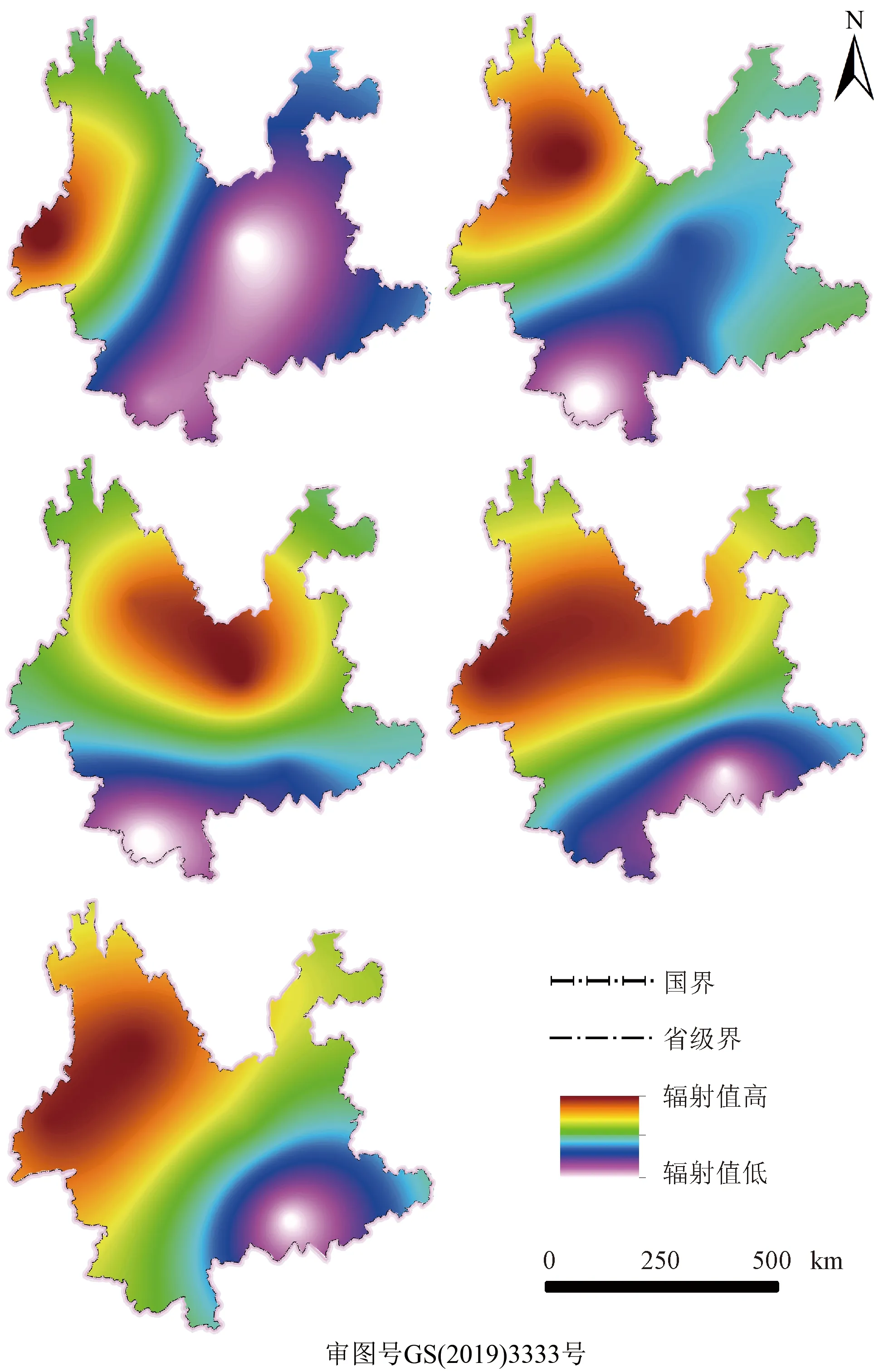
图4 MFCE模型估算结果各年空间分布图Fig.4 Spatial distribution of MFCE model estimation results by year
最低,在16.21~33.73 MJ/m2,证明本文方法与其余模型相比在结果拟合效果以及偏差均达到了相对最优化。多因子综合估算模型的月值均方根误差对比其余模型虽然有明显改善,但就自身而言模型结果的偏差还有待进一步提高,由于数据的精确程度等原因,本文研究中使用月为计算单位,测算尺度有待后续提高。

