基于边界积分方程求解二维移动滚动接触问题

舒小敏， 米栋

(中国航发湖南动力机械研究所， 株洲 412002)

工程机械中存在广泛的移动或滚动类接触问题。常见的移动接触有机床中直线导轨、移动导轨等，常见的滚动接触有机车轮轨、轴承中滚动体等。相对运动(移动或滚动)作用下产生循环接触载荷，容易使接触载荷影响区域内会出现接触疲劳现象(裂纹萌生与扩展)。典型的如高速铁路、普速铁路和城市轨道交通中的轮轨滚动接触疲劳，一直是研究中的技术难题之一[1]。此外工程实际中，由于两个接触体之间的相对运动，接触面间将由于摩擦而产生大量的热，进一步导致接触表面的热弹性变形和接触损伤[2]。因此，接触问题一直是研究关注的重点[3-7]。

不管是相对运动导致的接触损伤，还是循环载荷作用下导致的接触疲劳，接触应力都是影响接触损伤或接触疲劳重要参数。求解相对运动(移动/滚动)作用下的接触应力是研究接触损伤或疲劳的基本条件。

工程实际中结构复杂，常见接触解算法有：有限元法[5]、边界元法[6]、比例边界有限元法[7]。以上3种方法，不管采用何种方法，由于接触体之间相对运动，即使最初采用的是匹配网格(接触区两接触面节点一一对应)，相对运动(移动/滚动)后，节点将不再一一对应，变为非匹配网格。非匹配网格中不能保证全局平衡，可能会出现压力波动问题[8]，影响接触应力计算精度。

减少压力波动的直接方法是将非匹配网格变成匹配网格。在边界元法接触分析中，文献[9]采用了可动节点法，可保证移动或滚动后节点一一对应。不过，由于相对位置的变化，积分单元中出现相距很近的两节点将难以避免，在边界积分中将引入奇异积分难题。在有限元法接触分析中，文献[10-12]采用了可变节点的单元，实现节点一一对应，并应用到弹塑接触性问题及大变形接触问题中。比例边界有限元法中，文献[13-14]通过插入节点的方法在准静态接触问题中实现节点一一对应，而文献[15]采用自适应网格法减少压力波动。文献[10-15]中的方法，目前还未推广到移动或滚动接触中。

相对运动过程中，可能接触区位置一直变化，为精确模拟接触区应力集中现象，则需对所有可能接触区进行网格加密。以移动接触问题为例，在移动过程中可能接触区不断变化。为精确模拟移动接触过程中接触区的应力集中现象，需对移动过程中所有可能接触区进行网格加密。而实际移动过程中，某一时刻的可能接触区却远小于所有可能接触区，大范围的网格加密影响计算效率、增加计算成本。

为解决移动或滚动滚动接触中，非匹配网格引起的接触压力波动及避免在所有可能接触区进行网格加密，现采用网格更新法[16]保证接触区网格一一对应，并保证仅当前时刻可能接触区网格需加密。为减少网格更新数量，本文研究采用边界积分方程求解，这是由于边界积分方程中仅边界网格需离散[17-18]。为避免移动滚动后边界积分重复计算，本文研究采用旋转坐标系法，推导出移动滚动前后时刻边界积分方程的等价性，结果只需对更新的单元和节点进行积分，其他积分可直接利用上一时刻的积分数据。基于以上方法，本文研究提出二维移动滚动接触问题解方法，并通过数值算例验证本文方法的有效性。

1 边界积分方程的等价

1.1 边界积分方程

对于弹性问题，在不考虑体力的情况下，每个体的边界积分方程[17-18]为

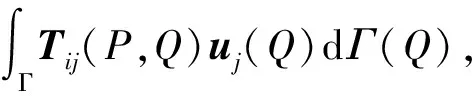
P，Q∈Γ

(1)

式(1)中：uj和tj分别为位移和面力分量；Uij和Tij分别为位移和面力核函数或基本解；cij(P)为关于体边界Γ布置系数矩阵；P、Q为物体边界Γ上的点。

在二维(i，j=1，2)平面应变问题中，位移和面力基本解对应表达式为

(2)

(3)

式中：r为源点P到场点Q的向量；r为点P和Q之间的长度;n为场点Q处的外法向；ri和ni为向量r和n的在i方向的导数；δij为克罗内克函数；G和v分别为剪切模量和泊松比，弹性问题中其值大小不变。

1.2 边界积分方程等价

边界积分方程等价，根据式(1)～式(3)要求源点P和场点Q之间的向量r无变化，同时Q处的外法向n不变。

如果坐标系不变，即不同时刻采用相同的坐标系。如图1所示，按w角速度滚动的物体，在不同时刻，若均采用时刻a的xa-o-ya坐标系，那么时刻a和时刻b比较，源点P到场点Q的向量r及场点Q处的外法向n均发生变化，边界积分方程不等价。因此，b时刻需要重新计算边界积分。

采用旋转坐标系法，即坐标系随物体一起旋转，则可推导出边界积分方程等价。即在图1中a时刻采用坐标系xa-o-ya，而b时刻采用坐标系xb-o-yb，那么a和b时刻比较，源点P到场点Q之间的向量r没有变化，且场点Q处的外法向n无变化。因此a时刻和b时刻边界积分方程完全等价，b时刻的边界积分可直接使用a时刻积分数据。

对于移动体问题，在图2中移动体以速度v0运动，同样采用旋转坐标系法，a时刻采用坐标系xa-o-ya，而b时刻采用坐标系xb-o-yb。由于无旋转，坐标系方向不变。a时刻和b时刻源点P到场点Q之间的向量r无变化，且场点Q处的外法向n无变化，因此a时刻和b时刻边界积分方程完全等价。

图1 不同时刻滚动示意图Fig.1 Rolling diagrams at different moments

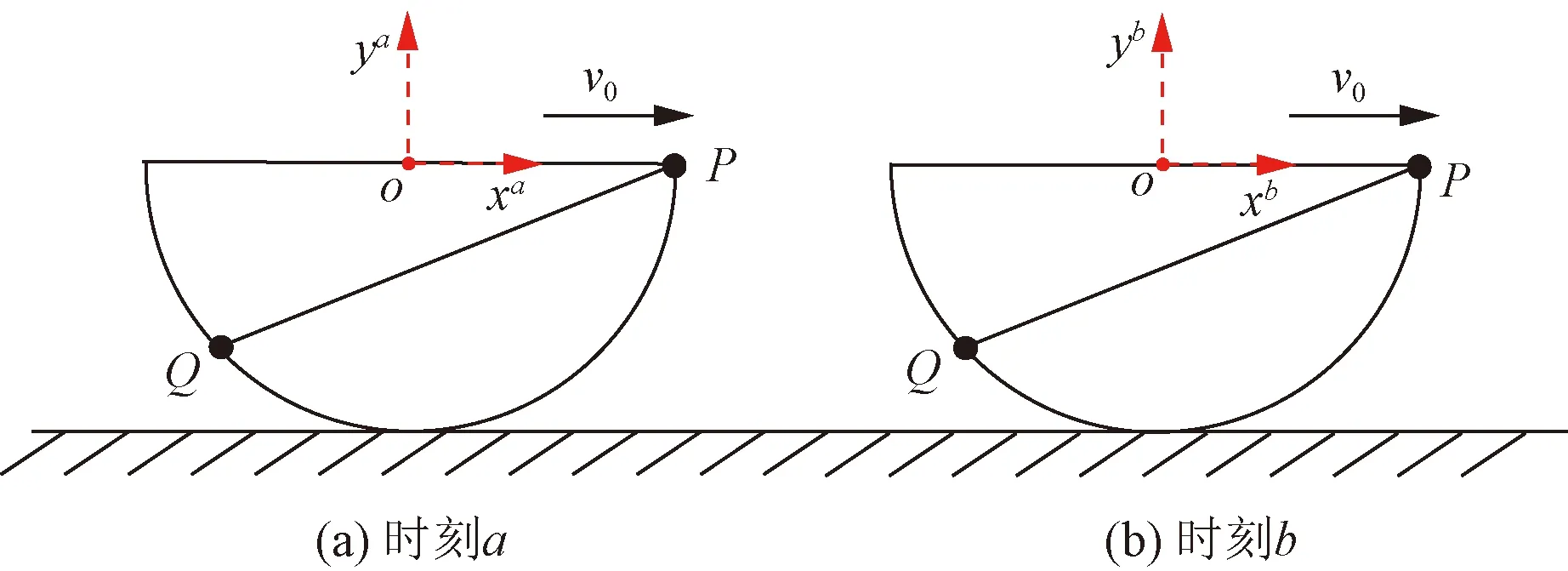
图2 不同时刻移动示意图Fig.2 Sliding diagrams at different moments

采用旋转坐标系法，如果网格离散相同，移动或滚动下一时刻则可利用上一时刻的边界积分数据，避免各时刻重新计算边界积分。

2 接触描述及坐标更新

2.1 接触点对法向坐标定义

考虑如图3所示两接触体边界上的接触点对，即a和b，接触区的公共法向量定义为

(4)

式(4)中：EA、EB分别为接触体A、B的杨氏模量；nA和nB为接触点a、b处的法向量。

切向量τ可通过旋转法向量90°得到。接触点对由最近投影点决定。在本文研究中，刚度较小接触体上的节点投影到另一刚度较大的接触体上，更大刚度体的法向量用于决定最近投影点。公共法向量仅用于确定接触区面力和位移的法向方向，并不用于确定最近投影点。

图3 公共接触法向量定义Fig.3 Definition of the common contact direction

2.2 无摩擦接触约束

在无摩擦接触中，可能接触区只有非接触和滑移接触状态存在。对于非接触状态，法向和切向面力均为零。

(5)

(6)

对于滑移接触状态，法向间隙为零，切向面力为零；此外节点对上的面力大小相等：

(7)

(8)

式中：uj和tj为加载后位移和面力，其中j=n,τ；A、B为对应的接触体；g为初始法向间隙。

2.3 坐标更新

采用旋转坐标系法，即坐标系随物体一起旋转，可保证单个体的边界积分方程在移动或滚动前后时刻的等价性。不过在接触问题中，需建立接触约束关系如式(7)所示，而接触约束关系的建立需要在一个统一的坐标系下描述。因此，移动滚动后需对坐标进行更新。

2.3.1 移动坐标更新

如图2所示，若移动的距离为L，移动的单位方向向量为(vx，vy)，则移动后的点坐标为初始坐标值(x，y)加上其在移动方向的移动距离，坐标值更新可表示为

(9)

2.3.2 定轴转动坐标更新

如图4所示，假设点A绕圆心C转动，坐标(xc,yc)则点A相对于圆心C的坐标为

(10)

式(10)中：R为定轴转动半径；α为点A相对于水平位置的夹角，如图4所示。点A转动θ角之后到达点A′的位置，它相对于圆心C的坐标为

(11)

点A′相对于圆心C的坐标可写为

(12)

将(Rcosα，Rsinα)用点A的坐标公式[式(10)]代替，则点A′相对于坐标原点O的坐标为

(13)

式(13)即为定轴转动一定角度后点的坐标值。只要知道定轴转动中心、初始点坐标及转动角度，利用该公式就可进行坐标更新。

图4 定轴转动Fig.4 Fixed axis rotation

2.3.3 滚动坐标更新内容

滚动具有定轴转动的特点又有移动，它等价于在定轴转动基础上再加上移动。滚动后的坐标更新需结合式(9)和式(13)，坐标更新公式为

(14)

3 网格更新及其积分计算

3.1 网格更新法

图5为滚动接触相邻两时刻的可能接触区(阴影部分)。图5(a)对应上一时刻，可能接触区为e。图5(b)对应当前时刻，可能接触区为f。从图5(b)中可看出，当前时刻是上一时刻点A′运动到点A的状态。在当前时刻中，既存在当前时刻的可能接触区f，也存在上一时刻的可能接触区e。

网格更新中，保证仅当前时刻可能接触区网格需加密。因此对于当前时刻，可能接触区f的网格需要加密更新。同时当前时刻中，上一时刻的可能接触区e不再是可能接触区，网格不需要加密处理。因此当前时刻中，上一时刻的可能接触区e的加密网格需变为一般网格，网格需更新。

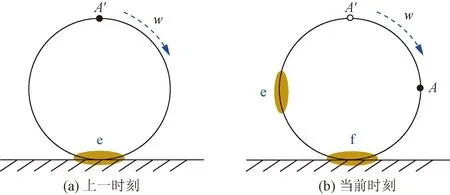
图5 滚动前后接触区域变化Fig.5 The changes in potential contact area after rolling

总之，网格更新就是将上一时刻可能接触区的加密网格更新为一般网格；同时将当前时刻可能接触区网格更新为加密网格。采用该方法后，仅当前时刻可能接触区的网格进行了加密。不会在移动或滚动多次后，网格不断增加。

3.2 积分计算

采用网格更新法后，部分网格单元进行了更新，即网格单元发生了变化，这些更新网格单元对应的积分仍需重新计算。

首先，根据单元更新情况，将离散后的节点分为新节点和旧节点。旧节点的定义为：节点在单元中的位置没有变化且与该节点相连的单元也无变化。其他不满足旧节点定义的节点，则为新节点。为说明这一定义，用图6进行阐述。

在图6所示的网格更新中，单元α和β更新为4个子单元α1、α2、β1和β2。更新后所有实心圆点为旧节点，新节点用空心圆点表示。节点P和Q位置虽然无变化，但与其相连的单元变化了。根据新旧节点定义，P和Q为新节点。

其次，根据新旧节点定义新旧单元。旧单元的定义为：全部为旧节点的单元。其他不满足旧单元定义的单元为新单元。

采用旋转坐标系法，旧单元和旧节点对应的积分系数可从上一时刻的积分数据中提取。因此，网格更新后，只需重新计算新节点和新单元对应的边界积分。不过，并非所有时刻都存在着上一时刻。最初计算时，没有上一时刻。因此，最初时刻中将所有的单元和节点全部定义为新单元和新节点，这时所有的单元都要进行积分计算。通过此次计算，存储相关积分数据。以后时刻网格无变化，则可利用上一时刻的积分数据，避免重复计算积分。

图6 网格更新示意图Fig.6 Schematic diagram of mesh updating

4 移动滚动接触算法流程图

图7为本文移动滚动接触问题解算法流程图。接触求解具体可参考文献[6，19]，运动是否终止为用户输入参数。

采用图7中算法求解移动滚动接触问题，主要优势如下：利用网格更新，保证仅当前时刻可能接触区网格需加密，同时实现接触区节点一一对应(匹配网格)，避免接触区压力波动问题[8]。此外采用旋转坐标系法，移动滚动前后时刻边界积分方程等价，避免未更新网格移动滚动后积分重复计算。

图7 移动滚动接触算法流程图Fig.7 Algorithm flowchart for sliding or rolling contact problems

5 数值算例

本节给出了两个无摩擦数值算例，用于证明本文方法的有效性。第一个是移动Hertz接触问题，另一个为滚动接触问题。

5.1 移动Hertz接触

如图8所示，一个弹性半圆(半径R=8 mm)在一个刚性体表面匀速移动。计算中取刚性体杨氏模量为弹性体杨氏模量的十万倍，此时可完全等价为刚性体。几何尺寸、边界条件、杨氏模量E、泊松比μ和载荷p情况如图8所示。

图8所示的无摩擦问题，有解析解存在[4]。根据解析解，接触半宽b的计算公式为

(15)

而接触法向压力pn的计算公式为

(16)

根据图8中的材料及载荷参数，接触半宽b=0.544 6 mm。本文方法和解析解对比如图9所示。

虽然半圆向前移动了一段距离(L=1，2，3，4 mm)，但图9中本文方法所有接触压力结果完全一

图8 Hertz接触问题Fig.8 Hertz contact problem

图9 移动不同距离的接触压力图Fig.9 Contact pressure plots with different sliding distances

致。这是由于另一接触体为刚性体，在刚性体表面上移动，任意位置的接触压力是相同的。此外图9中解析解和本文方法结果几乎完全重合，表明在移动接触问题中，本文网格更新法及边界积分等价法的有效性及准确性。

5.2 滚动接触

如图10所示，一个空心圆轮(半径R=5 mm)在一个拱形基座上匀速滚动，几何尺寸在图10中给出。黑色实线空心圆轮对应着初始时刻；红色虚线圆轮对应着滚动距离L=6 mm时的圆轮，此时模型对称。两接触体的材料参数相同：杨氏模量E=2 000 MPa、泊松比μ=0.3。边界条件为：基座两底端平面固定，载荷施加在空心圆轮孔的下半部分，压力大小为

(17)

式(17)中：x和y为滚动更新后坐标值；L为滚动距离，初始时刻L=0。该载荷公式的含义是只有空心圆轮孔的下半部分承受压力载荷，且滚动中下半部分承受载荷相同。

计算了滚动距离L=0、3、6 mm时的应力分量(Syy)，结果如图11所示。此外为证明本文方法的有效性，计算了若初始时刻L0=6 mm(等价于滚动距离L=6 mm)的应力，如图12所示。

滚动距离L从0～6 mm，接触中心逐渐逼近拱形基座对称面，且L=6 mm时接触中心与基座半圆之间厚度最小。对于相同载荷，接触中心与基座半圆间y方向厚度越小，引起的变形更大，应力越大。

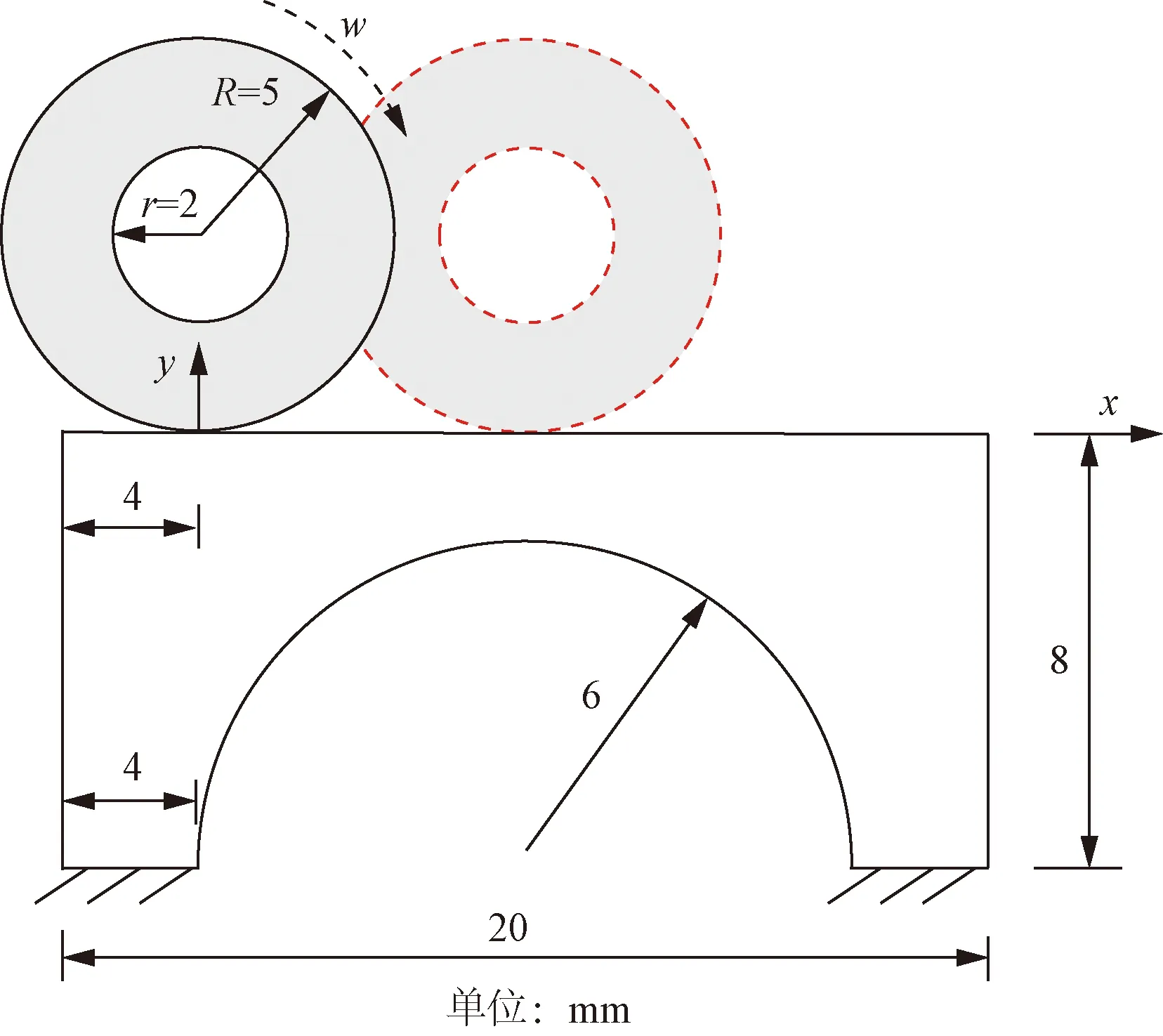
图10 滚动接触几何模型Fig.10 Geometric model of rolling contact

图11 不同时刻应力图Fig.11 Stress map at different moment

图12 初始时刻L0=6 mm的应力图Fig.12 Stress map at the initial time L0=6 mm

从图11可看出，随着接触中心与基座半圆间y方向厚度越来越小，接触中心处应力值逐渐增大，符合预测。

图12为若初始时刻L0=6 mm的应力图，此时模型和载荷对称，应力结果应对称。从图11(c)中可看出，采用本文方法滚动L=6 mm时的应力结果不仅对称，而且该结果与图12应力云图几乎完全一致，表明在滚动接触问题中，本文网格更新法及边界积分等价法的有效性及准确性。

6 结论

基于边界积分方程法对移动或滚动接触问题进行了求解，得出如下结论。

(1)采用网格更新法，保证仅当前时刻可能接触区网格需加密，从而避免了移动或滚动过程中所有可能接触区都需要网格加密的问题；并保证了接触区节点一一对应，保证接触应力的精度。

(2)采用旋转坐标系法，推导出了移动或滚动前后时刻边界积分方程的等价性。因此，下一时刻积分计算可直接利用上一时刻的积分系数，减少积分重复计算量。

(3)基于网格更新法、旋转坐标系法和边界积分方程法提出了移动或滚动接触问题解方法，并利用数值算例证明了本文方法的有效性。

(4)虽然本文研究局限于二维移动滚动接触问题，但本文方法却并不局限于二维问题，可推广到三维移动滚动接触。