基于矩阵博弈的近距空战自主机动决策方法

王芳杰, 黄 鹏, 张子俊, 孙 冲

(1. 西北工业集团有限公司, 西安 710005; 2. 西北工业大学, 西安 710072)

0 引 言

当前, 无人机越来越广泛的应用于各领域, 世界各国都在积极研制无人机, 无人机的出现也将改变未来的空战态势, 成为决定战场的重要力量[1-2]。 其中, 无人机的智能化水平将是无人机技术发展的关键, 如何使得无人机能够进行自主感知、 决策进而完成任务, 具有重要的研究价值[3]。

对于空战无人机自主决策的研究, 前人主要从基于专家知识库、 基于博弈论等方向进行了很多探索。 在专家知识库方面, 王锐平等[4]提出了一种基于知识库建立的空战仿真模型, 该模型是一套基于机动动作库的快速响应自主空战机动决策系统模型, 可以使无人机根据实时战场环境, 实现快速自主决策空战模拟飞行; 李维等[5]提出一种基于知识库的自主决策方法, 通过动态贝叶斯网络模拟人对态势的认知, 通过产生式规则进行决策。 在博弈论方面, 徐光达等[6]提出了一种基于双矩阵对策的空战自主机动决策算法, 对传统的“二人零和有限对策”模型进行了一定的改进; 李守义等[7]提出了一种非完备策略集下的博弈决策方法来解决无人机群的决策序列问题; 赵明明等[8]提出一种采用量子粒子群算法在模糊策略下博弈的纳什均衡求解方法, 通过求解模糊子集来获得博弈支付矩阵, 进而获得最优选择策略; 李亿俍等[9]针对固定翼无人机目标-攻击-防御三方集群对抗场景, 提出了一种基于微分博弈的集群攻防决策算法, 实现了包括目标-攻击-防御三种角色的三方集群攻防空战决策。

专家知识库是由专家根据实际空战中最常用的机动方式总结提出的, 能够指导无人机进行有效的机动决策。 同时, 空战双方的对抗特性决定了其可以利用矩阵博弈的方法对空战机动决策问题求解。 前人做的很多研究都对无人机的自主决策问题提出了针对性的解决方法, 但无人机采取的机动动作往往是离散的, 没有考虑成套的战术动作。 为了提高算法的实用性与真实性, 本文首先构建了无人机与导弹模型, 将成套的机动决策动作纳入专家知识库中, 并将矩阵博弈与构建的专家知识库系统相结合, 通过态势函数对空战形式进行分析, 为无人机提供了一套自主机动决策模型。

1 UCAV六自由度飞行动力学模型搭建

UCAV飞行动力学系统建模是智能空战研究的基础。 UCAV飞行动力学系统仿真实际是对其空气动力特性进行仿真, 计算UCAV的六自由度非线性全量运动方程, 仿真UCAV远程对抗过程中的力和力矩, 以及大气环境对飞行的影响, 即建立飞行系统仿真数学模型。

令海平面标准大气参数为高度h=0 m, 大气温度T0=288.15 K,g0=9.806 65 m/s2, 大气密度1.225 kg/m3, 大气压力101 325 N/m2, 则温度随高度的变化为

(1)

当h>11 000 m时, 进入同温层。

压力的计算公式为

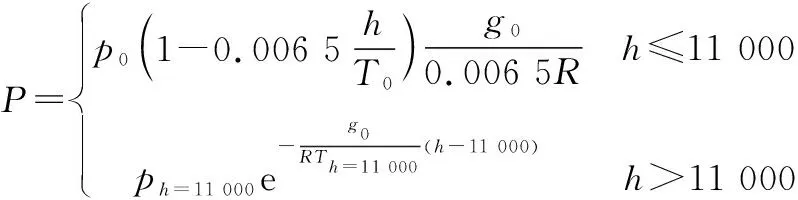
(2)

则密度、 声速和重力加速度的计算公式为

(3)

(4)

(5)

式中:R=287.05为气体常数;Re=6 371 000 m为参考地球半径。

这里给出UCAV于机体坐标系下的运动学以及动力学模型:

UCAV机体轴系包含三个方向的位置、 速度以及欧拉角的计算公式表示成矩阵形式为

(6)

式中:φ,θ,ψ分别为滚转、 俯仰、 偏航角;p,q,r分别为绕机体轴三轴的角速度, 定义式如下:

(7)

沿机体坐标系三轴的速度u、v、w与滚转、 俯仰、 偏航角关系如下:

(8)

UCAV于地面坐标系下的位置描述如下:

(9)

2 导弹六自由度动力学模型搭建

2.1 弹体动力学方程

本节将进行未简化弹体动力学方程的相关模型搭建, 包括:

(1) 气动力矩计算部分

(10)

(2) 姿态动力学部分

(11)

(3) 姿态运动学部分

(12)

(4) 气动力计算部分

(13)

(5) 质心动力学部分

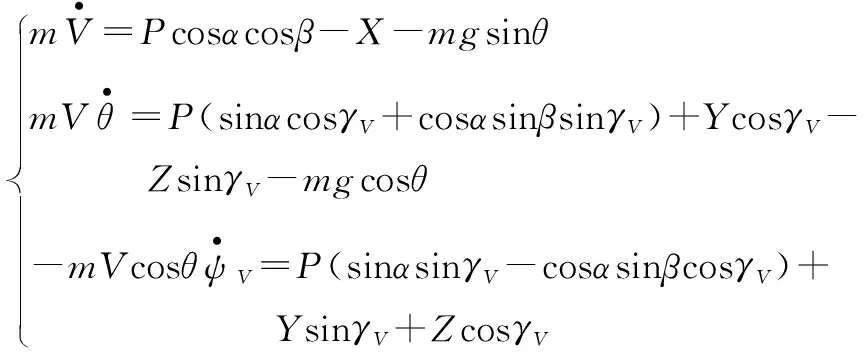
(14)

(6) 角度几何关系补充方程

(15)

特别说明, 对于不同的导弹, 其对应的气动参数方程解算部分将会出现不同结果。

2.2 导弹攻击区包络解算

目前大部分空战态势函数的构建单纯基于特定假设条件, 存在定量分析的问题, 为了使UCAV近距空战决策更具有客观性, 考虑基于导弹攻击区的实时解算的空战态势评估方法。

导弹攻击区是以攻击机作为参考, 在满足一定的攻击条件下, 攻击机发射导弹能以一定的概率命中目标的目标初始位置的范围。 按照目标运动方式的不同, 导弹攻击区包络可以分为导弹可攻击区和导弹不可逃逸区。

影响导弹攻击区的因素主要有: 导弹的性能、 载机和目标机的运动状态[10]。 本文以导弹、 载机、 目标的动力学模型为基础, 实时解算导弹攻击区包络。

2.2.1 导引率模型

采用比例导引法, 即控制导弹在飞向目标的过程中, 使导弹速度方向变化率与目标视线变化率成比例, 其模型如下:

(16)

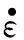
弹上导引头最大角速度限制为

(17)

2.2.2 导弹运动约束条件

导引头动态视场角限制为

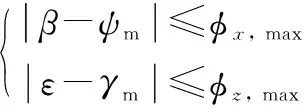
(18)

导弹飞行时间限制为t≤tmax, 目标影像探测距离限制为

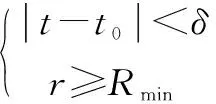
(19)

引信最小遇靶相对接近速度限制为

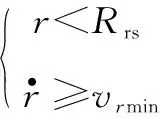
(20)

导弹飞行高度限制应为Hm∈(0.2～20 km)。

2.2.3 基于黄金分割搜索算法的可发射边界求解策略

通过黄金分割搜索算法[11]对导弹的可发射策略进行求解。 首先在导弹离轴角允许的范围内, 确定目标初始位置相对于载机的方向; 预估初始距离范围[a0,b0], 计算黄金分割点R0=a0+0.168(b0-a0); 以分割点位置为目标初始位置进行仿真, 根据导弹性能约束判断导弹是否命中目标。 在远边界搜索中, 如命中目标, 令a1=R0,b1=b0; 如未命中, 则令a1=a0,b1=R0; 重新循环计算, 直到求出满足约束|bi-ai|<δ的边界为止。 近边界搜索与远边界类似, 在命中目标时, 令ai=ai-1,bi=Ri-1, 否则令ai=Ri-1,bi=bi-1。 距离找到后, 改变目标方位角或俯仰角, 重新计算, 直到导弹导引头可探测的角度搜索完毕为止; 最后, 所记录的Ri-1值即为导弹可发射区的边界值。

近界搜索与远界搜索类似, 只是在迭代中若导弹击中目标, 则令ai=ai-1,bi=Ri-1; 否则令ai=Ri-1,bi=bi-1。

3 专家战术机动动作知识库构建

机动动作库是专家知识库的一种, 由高级飞行员或飞行专家通过自身经验知识指导构建。 优秀的机动动作库可以为无人机飞行提供高效的成套机动方案, 当无人机在空战格斗中处于相应态势时可以直接采用对应的最佳机动动作, 使得无人机在空战格斗中机动更灵活、 决策更快速。 考虑到飞机载荷与飞机机动能力, 常用的机动动作可以分为进攻性、 防御性以及大进入角三种基本机动形式。

典型的机动动作有筋斗机动, 破 S 机动, 蛇形机动, 迎头/尾追转弯, 水平剪刀机动, 英麦曼机动等。 根据常用的空战机动动作形式, 本文针对不同高度与不同速度条件下的空战场景, 提出了一种包含多套机动动作的专家知识库。 首先通过模型实飞获得真实飞行数据, 并将其代入到UCAV动力学与控制模型中, 求解获得模型实飞的位置坐标变化曲线。 然后, 通过将位置坐标数据代入到三自由度动力学模型汇总, 反向求解三维过载。 最终将整套机动动作的过载按照时间序列的方式形成专家知识库。

“基本操纵动作库”主要是美国国家航空咨询委员会(NASA)学者根据空战中最常用的机动方式提出的[12], 主要包括: 最大加速, 最大减速, 稳定飞行, 最大过载爬升, 最大过载俯冲, 最大过载左转, 最大过载右转。 这类机动动作的设计主要源于飞机在空间中各个方向采取的机动, 并且加以极限操纵方式便于控制量的表述。 虽然基本操纵动作库的控制量描述简单, 并且可以避免典型战术动作库存在的矛盾, 可以由这7种机动方式组合出很多机动动作来, 但是这种动作库的设计比较粗糙, 都采取极限操纵显然不符合空战实际。 考虑到决策的实时性、 灵活性的要求, 基本操纵动作库作为机动决策的动作集模型更具有优势。 因此, 主要针对基本操纵动作库进行如下改进完善:

(1) 加入新的基本操纵方式扩充动作库, 以便能够组合出空战中的所有战术动作。

(2) 对每个动作的操纵进行细化, 不仅是极限操纵。

可得到改进后的基本操纵动作11种: 匀速前飞, 减速前飞, 加速前飞, 左转, 右转, 爬升, 俯冲, 左爬升, 右爬升, 左俯冲, 右俯冲, 如图1所示。

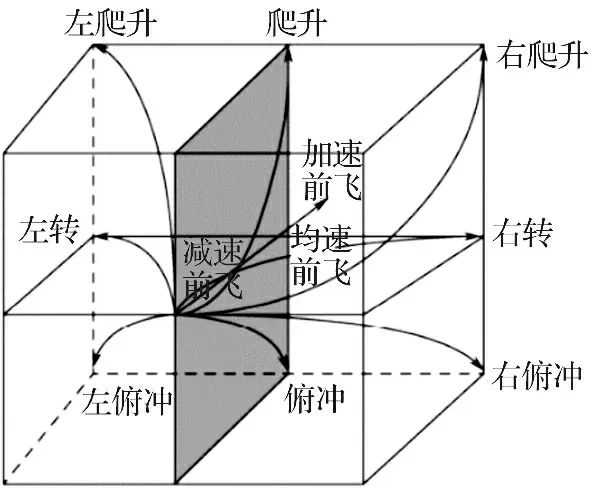
图1 改进后的基本机动动作库Fig.1 Improved basic maneuver action library

11种基本操纵动作控制量参数, 如表1所示。 将表中机动参数分别代入飞行器的三自由度质点动力学模型中, 进行一步积分运算后, 便可得到下一时刻目标机动的状态预估。

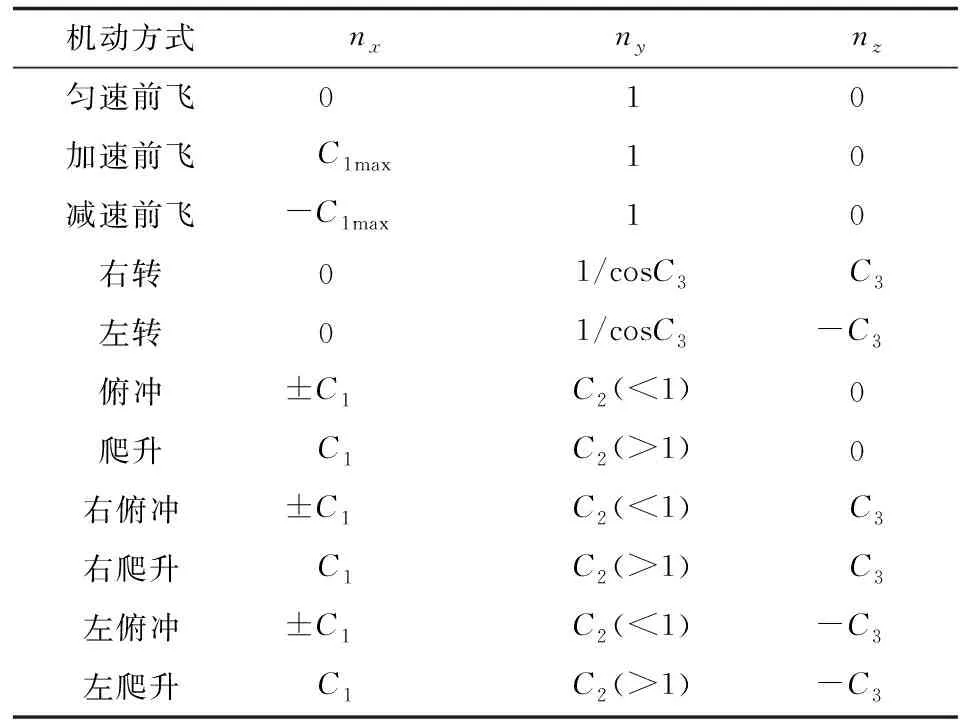
表1 基本动作库控制量参数Table 1 Basic action library control quantity parameters

4 基于矩阵博弈的机动决策模型构建

4.1 空战机动决策评价函数构建

空战机动决策评价函数的目的是通过评价函数的构建, 导引无人机稳定接机和有效攻击占位。 在保持自身态势优势的同时, 充分发挥武器系统的战术使用性能, 快速消灭目标。 基于导弹的作战使用实际, 本文将构建包含角度、 距离和能量决策因子的决策评价函数, 以期获得更大态势优势。

在进行相对状态计算和导弹可发射距离解算时, 为了简化计算过程, 本文忽略攻角对相对状态产生的影响, 即认为速度方向与 UCAV 机身轴线的方向保持一致。 某态势下, UCAV与目标机的相对位置关系, 如图2所示。

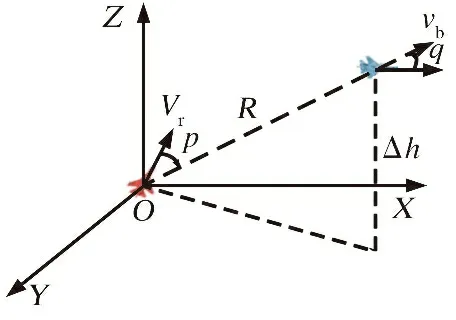
图2 UCAV相对位置关系Fig.2 UCAV relative position relationship

4.1.1 角度决策因子评价函数

空战过程中, 敌我双方UCAV空战角度态势分析如图3所示。

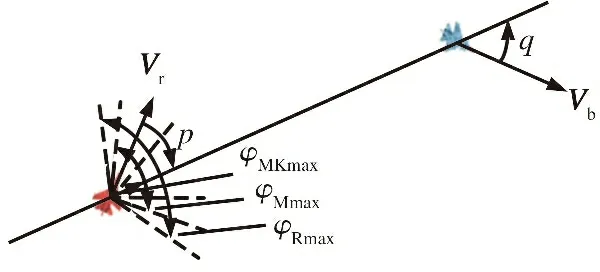
图3 敌我UCAV角度态势Fig.3 UCAV angle situation

图中, 假设Vr为我方UCAV的速度矢量;Vb为敌方UCAV的速度矢量;p为我方相对于敌方的方位角;q为敌方的进入角;φRmax为雷达的最大搜索角;φMmax为导弹最大离轴发射角;φMKmax为导弹不可逃逸区最大偏角。 同时, 规定方位角和进入角的方向是由速度矢量方向指向相对距离矢量方向, 且满足p∈[0, π],q∈[0, π]条件。

当我方UCAV方位角在雷达搜索角范围内或在导弹攻击范围内则占据攻击优势; 当敌方UCAV进入角小于我方UCAV逃逸角时, 我方的攻击优势较大。 根据上述关系, 可以分别构建我方UCAV方位角及敌方进入角优势函数。

方位角优势函数为

(21)

进入角优势函数为

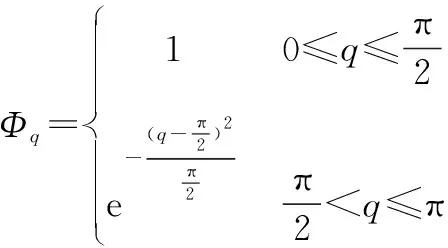
(22)

要达成最终的攻击条件, 不能单独只考虑其中一个角度参数, 需要同时考虑我方UCAV方位角和目标进入角, 因此, 构造角度态势优势函数为

ΦA=ΦpΦq

(23)

式中:ΦA∈[0, 1]为角度态势优势函数, 态势值越大优势越大。

4.1.2 距离决策因子评价函数

UCAV 与目标机相对距离位于当前态势下导弹可发射距离区间范围内, 构成导弹的稳定发射条件, 是空战机动决策的最终目的, 因此需要构建距离决策因子, 以实现对导弹可发射条件的有效导引。 为了提高导弹的命中概率, 当前态势下的发射距离判断值, 基于目标逃逸机动预估的导弹可发射距离解算值, 模型定义为

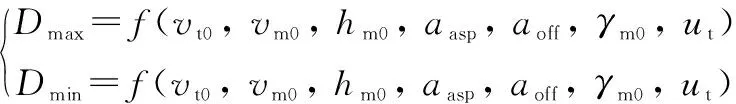
(24)

式中:Dmax和Dmin分别为当前态势下导弹可发射距离的最大、 最小值。 构建距离决策因子ΦD为

(25)

式中:D表示当前 UCAV 与目标机的相对距离。

4.1.3 能量决策因子评价函数

空战能量主要包括动能和势能两个方面, 分别与速度和高度呈正相关。 一方面, 无人机所具备的能量越大, 其机动能力就越强, 可发挥的潜力就越大, 通过能量转化, 有助于快速攻击和优势机动占位; 另一方面, 高的能量有助于导弹攻击能力的充分发挥。 当导弹所具备的相对能量越大, 可攻击的范围就越大, 因此, 高的能量有助于导弹战术使用性能的充分发挥。 综合考虑动能和势能两个因素, 从UCAV机动角度构建能量决策因子ΦE为

(26)

式中:vu,hu分别为UCAV速度及高度;vt,ht分别为目标速度及高度。

因此, 导弹的综合决策态势函数为

Φ=k1ΦA+k2ΦD+k3ΦE

(27)

式中:k1,k2,k3分别为角度、 距离及能量的态势权重系数。

4.1.4 导弹攻击状态评估的权重因子分级模型

构建基于导弹攻击状态评估的权重因子分级自适应模型, 以满足导弹的作战实际条件。 在导弹未构成允许发射状态的前提下, 主要存在以下3种不同攻击状态:

(1) 当目标离轴方位角aasp过大, 使方位角p大于导弹发射时刻的最大离轴发射角φMmax, 即p>φMmax, 导弹导引头无法搜寻、 锁定目标。

(2) 方位角p满足离轴发射角限制, 存在可发射区间[Dmin,Dmax]; 相对距离D不在该区间范围内, 导弹无法有效杀伤目标, 即p≤φMmax,D∉[Dmin,Dmax]。

(3) 方位角p满足离轴发射角限制, 但受到其他因素限制, 当前状态下, 不存在可发射区间[Dmin,Dmax], 即p≤φMmax, [Dmin,Dmax]=(0, 0)。

在对导弹攻击状态评估的基础上, 设置权值对应规则如表2所示, 导弹攻击状态为(1)和(3)时, 其可发射距离解算结果为零, 此时应该给定可发射区间参考值[Dmin,Dmax], 以实现距离决策因子的有效输出和UCAV的有效导引。

表2 基于导弹攻击状态评估的决策因子权重Table 2 Decision factor weights based on missile attack state evaluation

4.2 基于矩阵博弈方法与专家知识库的近距双机对抗自主机动决策算法

基于矩阵博弈方法与专家知识库的近距双机对抗自主机动决策其基本的思路是首先计算当前态势下交战双方的态势值, 与专家知识库中的典型场景进行匹配。 当没有匹配的战术动作时, 通过构造衡量对抗的态势情况的目标函数, 计算每一个决策时刻交战双方在当前态势下的支付矩阵。 然后, 根据最大最小值原理求解支付矩阵的鞍点, 鞍点对应的机动动作即为当前无人机应采取的最佳机动动作。 流程如图4所示。

图4 矩阵博弈整体思路流程图Fig.4 Overall idea flowchart of matrix game

(1) 首先获得t0时刻我方的位置(x1,y1,z1)与敌方的位置(x2,y2,z2), 代入到构建的态势函数中, 计算当前状态下的态势值, 并与专家战术动作库中的机动动作进行匹配。 若有符合当前态势的机动动作, 则直接执行专家战术动作库中的动作。

(2) 当专家战术动作库与当前态势不匹配时, 为了对下一步的机动动作进行预判从而确定我方下一步的机动动作, 要在t0时刻双方位置态势的基础上, 进行一步预测。 通过飞行器三自由度质点动力学模型与机动动作结合, 以当前双方各自位置作为输入, 求解每一机动动作对应的下一时刻t1双方的状态。

(3) 通过相对运动模型与导弹攻击包络形成态势函数Φ, 将t1预测时刻一方的机动动作i、 另一方的机动动作j对应的双方位置、 相对角度等作为态势函数输入, 求解出机动动作i,j对应的态势函数值Sij, 其中(i∈m,j∈n), 填入支付矩阵第i行第j列中。 对双方每一个机动动作组合进行计算, 形成由敌我双方所有机动动作一一组合的对应的m×n维支付矩阵:

(28)

生成评价矩阵流程如图5所示。

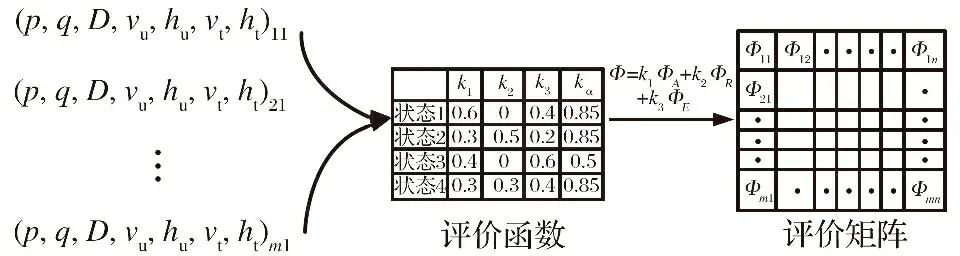
图5 评价矩阵生成流程图Fig.5 Flow chart for generating evaluation matrix

(4) 针对双方分别建立的各自的支付矩阵, 根据最小最大原则各自选择分数最大的机动方式, 选择的结果是达到了博弈论中的平衡点, 即“鞍点”:

(29)

根据该点在支付矩阵中确定敌我双方机动策略, 进而可以确定我方下一时刻的机动策略与动作。ν即为最大最小理论得解, 亦可以认为ν对应敌我双方无人机鞍点策略。 假设ν对应敌我双方策略为aij, 此时aij既是其所在列得最优策略, 也是其所在行的最差策略,i成为我方无人机的鞍点策略,j成为对方无人机的鞍点策略, 如图6所示。

图6 鞍点策略Fig.6 Saddle point strategy

图中, 横线和纵线组成的交点对应我方和对方无人机的策略, 红点对应敌我双方的鞍点策略。

5 仿真结果

本次仿真在北天东坐标系下进行, 设置UCAVA的初始位置状态为[xA,yA,zA]=[2 000, 2 000, 3 000], 初始速度、 航迹倾角、 航迹偏角为[VA,θA,ψA]=[200, 0, 0]; UCAVB的初始位置状态为[xB,yB,zB]=[2 000, 2 000, 6 000], 初始速度、 航迹倾角、 航迹偏角为[VB,θB,ψB]=[200, 0, 0]。 仿真中对UCAV的机动条件进行了一定限制, 其中UCAV飞行速度约束为Vlimit∈(90, 300) m/s, 最低飞行高度约束为Hlimit=500 m。 采用上述仿真条件进行为期50 s的双击博弈对抗, 其仿真结果如图7所示。

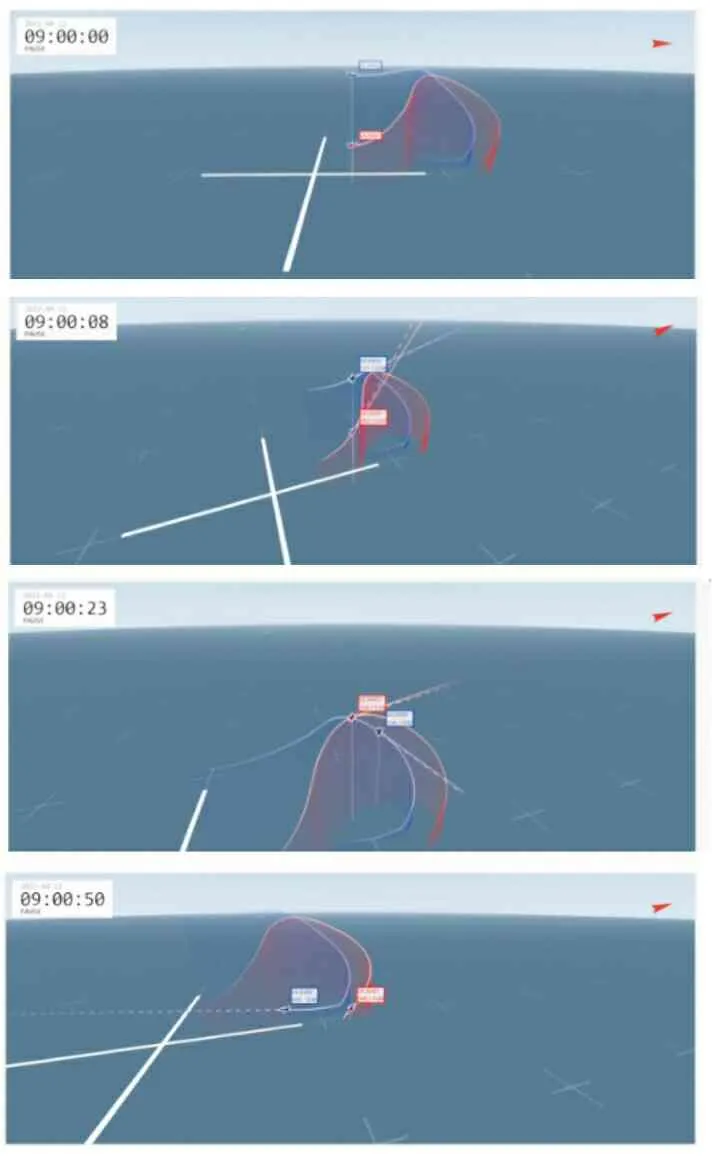
图7 UCAV第一次空战轨迹Fig.7 The trajectory of UCAV’s first air combat

从仿真中可以看出, 双方UCAV均使用基于本文提出的算法进行了有效的机动决策。 红蓝双方初始状态处于蓝方在红方上方占据高度优势。 红方试图攻击蓝方, 因此进行了爬升; 而蓝方试图攻击红方, 因此先向左进行机动。 蓝方为了规避红方的攻击同时能够占据优势, 试图通过右俯冲绕到红方身后, 红方也相应的进行了相应的右俯冲的机动动作。 本轮仿真的终止条件为仿真时间到, 并未出现UCAV击中目标的情况。

仿真过程中交战双方态势值的变化如图8所示。 从图中可看出, 红方UCAV使用本文提出的算法, 在10 s左右, 位于低位的情况下进行爬升以对敌方飞机形成攻击优势; 当敌方飞机采用右下俯冲进行躲避时, 同样采取右下俯冲占据攻击优势位置, 保持自身态势占优。

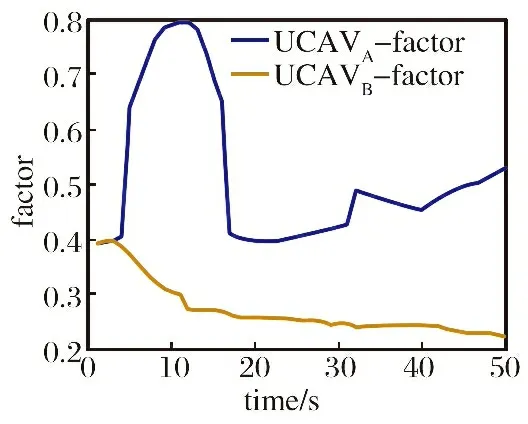
图8 第一次交战过程态势值变化曲线图Fig.8 Curve chart of situation value changes during the first engagement

进一步, 设置UCAVA的初始位置状态为[xA,yA,zA]=[10 000, -3 000, 5 000], 初始速度、 航迹倾角、 航迹偏角为[VA,θA,ψA]=[100, 3, 5]; UCAVB的初始位置状态为[xB,yB,zB]=[200, 3 000, 3 000], 初始速度、 航迹倾角、 航迹偏角为[VB,θB,ψB]=[200, 0, 0]。 其他仿真条件不变, 进行为期50 s的双机博弈对抗, 其仿真结果如图9所示。

图9 UCAV第二次空战轨迹Fig.9 The trajectory of UCAV’s second air combat

从仿真中可以看出, 红蓝双方初始状态处于迎头态势。 红蓝双方一开始并未进入雷达识别范围。 雷达识别到双方后, 蓝方试图攻击红方, 红方试图躲避蓝方的同时占据攻击态势, 因此开始进行向下俯冲。 蓝方根据算法判断, 也采取了俯冲机动。 由于红方为了占据攻击优势, 采取了左转弯机动, 蓝方为了避免自身处于劣势, 采取了爬升机动, 远离红方攻击区。 仿真过程中交战双方态势值的变化如图10所示。

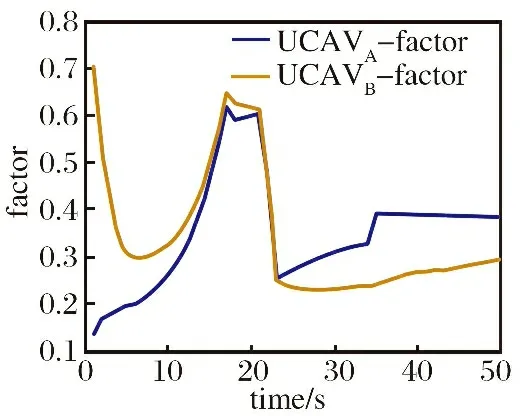
图10 第二次交战过程态势值变化曲线图Fig.10 Curve chart of situation value changes during the second engagement

从图10中可以看出, 最初蓝方占据优势态势, 此时红方进行前下方俯冲以躲避攻击区, 蓝方同样进行前下方俯冲指向红方, 双方态势同时增加; 红方为躲避攻击采取左下俯冲机动以提高自身态势值; 蓝方采取爬升机动躲避攻击区, 但红方态势增加更加明显并超过蓝方, 最终仿真结束时红方反超占据优势态势。

由以上两次仿真可以看出, 双方在均使用本文提出的算法的基础上进行了有效的实时机动对抗。 为了验证算法的实时性, 对50 s机动对抗的全程中每步决策时间的统计如表3所示。 可以看出, 每步机动决策时间短, 符合实时决策的需求。

表3 空战格斗仿真计算时间Table 3 Air combat simulation calculation time

6 结 论

本文针对UCAV空战过程中的自主机动决策问题, 提出了一种基于专家知识库与矩阵博弈的近距空战博弈对抗方法, 构建了包含离散动作与连续战术动作的专家战术机动动作库, 使得UCAV作出的机动决策动作更具合理性。 同时本文还将其与矩阵博弈方法相结合, 扩展了UCAV的机动决策能力, 有效提升了其自主机动决策的真实性与快速性。 通过仿真实验证明, 本文所提出的算法有效的提升了UCAV的自主机动决策能力, 其做出的机动动作更符合真实空战场景要求。