基于回归方法和神经网络的电弧增材制造单道成形形貌预测
李峰光,曹宜发,郭睿,姜淑馨,刘建永,胡胜波,戎博川
基于回归方法和神经网络的电弧增材制造单道成形形貌预测
李峰光1,曹宜发1,郭睿1,姜淑馨1,刘建永1,胡胜波1,戎博川2
(1.湖北汽车工业学院 材料科学与工程学院,湖北 十堰 442002;2.北京市房山区特种设备检测所机电一室,北京 102401)
针对电弧增材制造技术实际应用中工艺参数选取困难和成形结果难预测的问题,确定高效、准确的电弧增材制造单道成形形貌预测的数学方法,以快速、方便地选取丝材电弧增材制造工艺参数并指导成形质量控制。在单道单层丝材电弧增材制造实验的基础上,采用多种回归方法和神经网络方法分别建立焊接电流、电压和焊枪移动速度等多个工艺参数与增材层宽度、增材层高度及熔池深度等成形形貌参数之间的数学关系模型。电弧增材制造单道成形形貌与焊接电流、电压和焊枪移动速度显著相关,且各参数间存在非线性交互作用;采用多元线性回归法可较准确地预测单道增材层宽度,但对于增材层高度和熔深的预测效果较差;神经网络可良好地处理各工艺参数间复杂的非线性关系,其对增材层宽度、增材层高度和熔深的预测平均误差率分别为4.17%、6.60%和7.01%,显著优于多元线性回归法。采用神经网络法可以准确预测电弧增材制造单道成形的形貌参数,进而指导增材制造工艺参数的选取和成形质量的控制。
电弧增材制造;成形形貌;神经网络;H13钢;回归方法
丝材电弧增材制造(Wire and Arc Additive Manufacturing,WAAM)是一种快速近净成形制造工艺,因其材料利用率和成形效率高、制造成本低且增材件组织结构致密、力学性能好等突出优势而广泛应用于汽车、航空航天等领域的零部件制造和修复[1-4]。但目前丝材电弧增材制造技术仍存在工艺参数难选取、成形件性能难调控和成形结果难预测等问题[5-8]。根据不同的成形件结构和性能要求,研究者一般需要进行大量的单道单层电弧增材实验,通过单道成形形貌和性能的分析来确定合理的工艺参数,进而制定完整的增材制造工艺方案[9-13],所需物力、人力和时间成本均较高。部分学者在进行激光增材制造研究时提出,可在实验的基础上通过数学方法建立工艺参数与熔覆层形貌之间的关系模型,对熔覆层形貌进行预测以快速确定工艺参数,进而降低制造成本。相关学者开展了大量研究工作,证明了随机森林回归[14]、遗传算法[15-16]、线性回归[17]和神经网络[18-21]等方法均能较好地预测激光增材制造熔覆层形貌,其中线性或非线性回归方法和神经网络应用最为广泛[22-24],但相关数学方法在电弧增材制造形貌预测领域应用仍较少。石玗等[1]对金属电弧增材成形控制研究现状进行了较为详尽的文献调研研究,认为增材层宽度和高度等关键形状参数的精确控制是电弧增材制造成型控制最为重要的技术。目前,相关研究者已经建立了基于模糊控制方法的焊缝成形尺寸控制模型[25]、基于激光视觉传感器的增材层形貌控制模型[26]和基于单变量阶跃响应传递函数的增材层尺寸动态控制模型[27]等多种增材层形貌预测和控制模型,但相关模型均或多或少地依赖昂贵的硬件设备支持,尚未能大规模推广应用。因此,文中在单道单层电弧增材制造实验的基础上,利用多种回归方法和神经网络建立电弧增材制造工艺参数与其增材层形貌参数之间的数学关系模型,比较各方法预测的精确度,以期为后续研究中工艺参数的快速选取和成形质量控制提供参考。
1 实验方法
1.1 实验设备及方案
实验在自行搭建的数控丝材电弧增材制造系统上进行,该电弧增材制造系统主要由保护气系统、焊机(松下YD-350GR5型,熔化极活性气体保护焊)、送丝机构和数控机床(西门子802C型)4个部分组成,关键设备如图1所示。其中,焊机的焊接电流和电压可以分别独立调节,以控制热输入;通过数控编程控制机床带动焊枪以一定速度和路径运动而实现增材制造。增材实验所用基板为调质处理后的H13钢,焊丝名为GLG-H13,其成分如表1所示,直径1.2 mm。由于本文主要研究的是焊接电流()、电压()和焊枪移动速度()及焊道长度()4个参数对单道成形形貌的影响,结合笔者前期研究,选择保护气为85%Ar+15%CO2;焊接电流变化范围为80~160 A(送丝速度在1.7~3.7 m/min范围内与焊接电流自动匹配),焊接电压变化范围为18~22 V,焊枪移动速度变化范围为2~6 mm/s,焊接长度变化范围为50~150 mm;采用L25(56)的4因素5水平正交实验方案安排实验,如表2所示。
表1 GLG-H13焊丝成分

Tab.1 Composition of GLG-H13 welding wire wt.%
1.2 实验结果测量方法
电弧增材制造实验结束后,在每个单道增材层中部沿垂直于焊枪移动方向采用线切割方式取下试样,采用400#~1500#砂纸进行逐级打磨抛光,经无水乙醇清洗后,浸入(HF):(HNO3):(H2O)=1:3:7的腐蚀液中腐蚀10 s,磨样并机械抛光后在体视显微镜下观察增材层及熔池形貌。典型的熔池和增材层形貌如图2所示,其中,为增材层宽度,为增材层高度,为熔池深度,对每一试样均测量上述3个参数并填入实验结果表中。
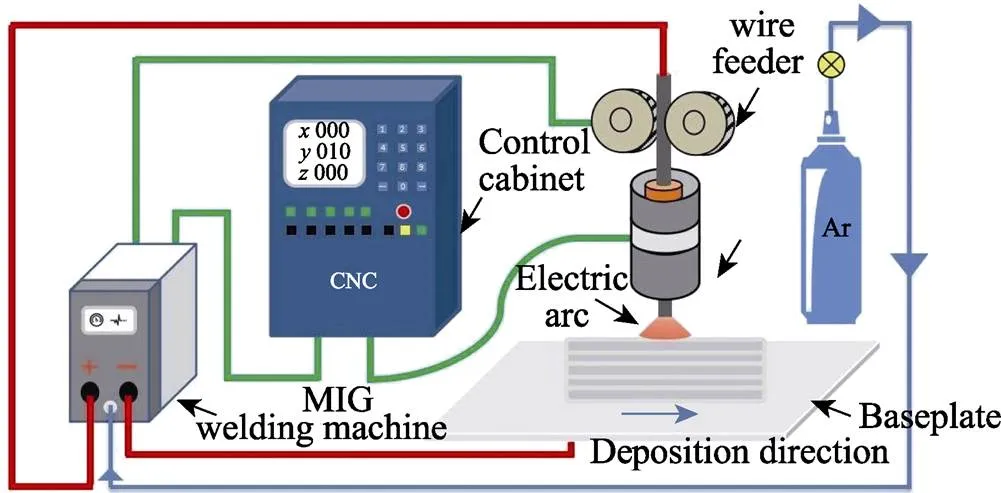
图1 电弧增材制造系统关键设备
表2 增材制造实验方案

Tab.2 Experimental scheme of additive manufacturing

图2 增材层形貌参数测量示意图
2 结果与分析
2.1 实验结果
各参数组合下电弧增材制造所得增材层宏观形貌如图3所示,部分参数组合下无法正常成形,未在图中列出。

图3 增材层宏观形貌
笔者团队在激光增材制造研究中发现,由增材热输入功率除以焊接速度计算得到的线能量L(即/,单位J/mm)与增材制造形貌间存在一定的关系[28],因此,文中针对每个参数组合均计算线能量并测量、和后得到表3所示实验结果。
表3 增材制造实验方案及结果
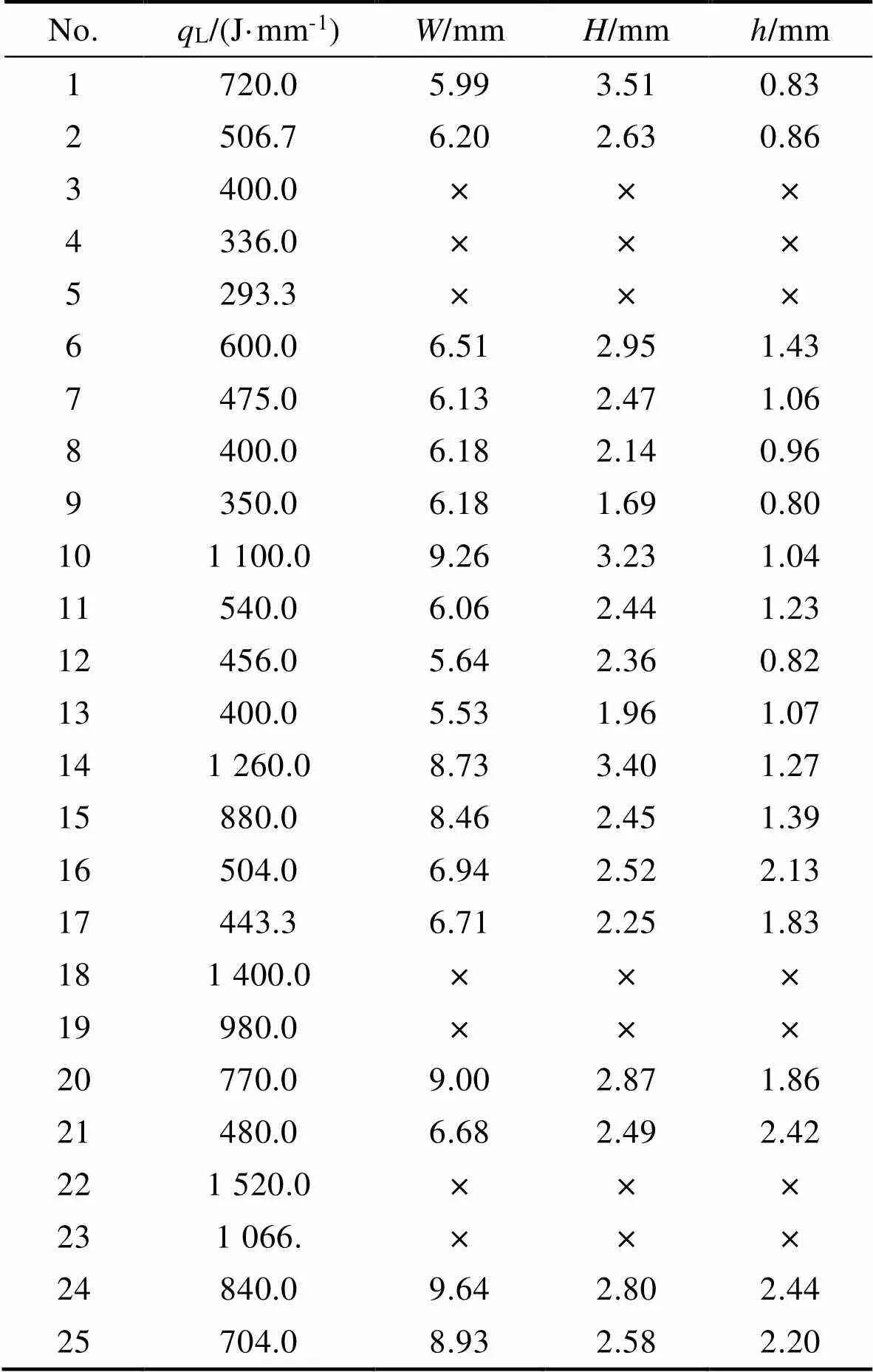
Tab.3 Experimental scheme and results of additive manufacturing
Note: "×" indicates that the specimen cannot be formed normally under this parameter combination.
根据表3中数据可知,各工艺参数会对增材制造单道成形的增材层宽度、增材层高度和熔深产生影响,在工艺参数选择不合理时,甚至无法成形。当线能量较低或较高时,均有较大可能出现无法单道成形的情况,但线能量的高低并不能直接决定增材是否成形。例如,在线能量较低时,第3组和第8组实验中线能量同样为400.0 J/mm,第8组参数条件下可以正常成形,但第3组条件下无法成形;同样,在线能量较高时,第23组(线能量1 066.7 J/mm)无法成形,但与之线能量接近的第10组(线能量1 100.0 J/mm)和线能量更高的第14组(线能量1 260.0 J/mm)均能正常成形。为进一步分析线能量与增材层宽度、增材层高度和熔深之间的关系,将无法成形的7组实验组合剔除,剩余的18组数据按照线能量排序后,绘制线能量L与增材层宽度、增材层高度及熔深的关系曲线,如图4所示。
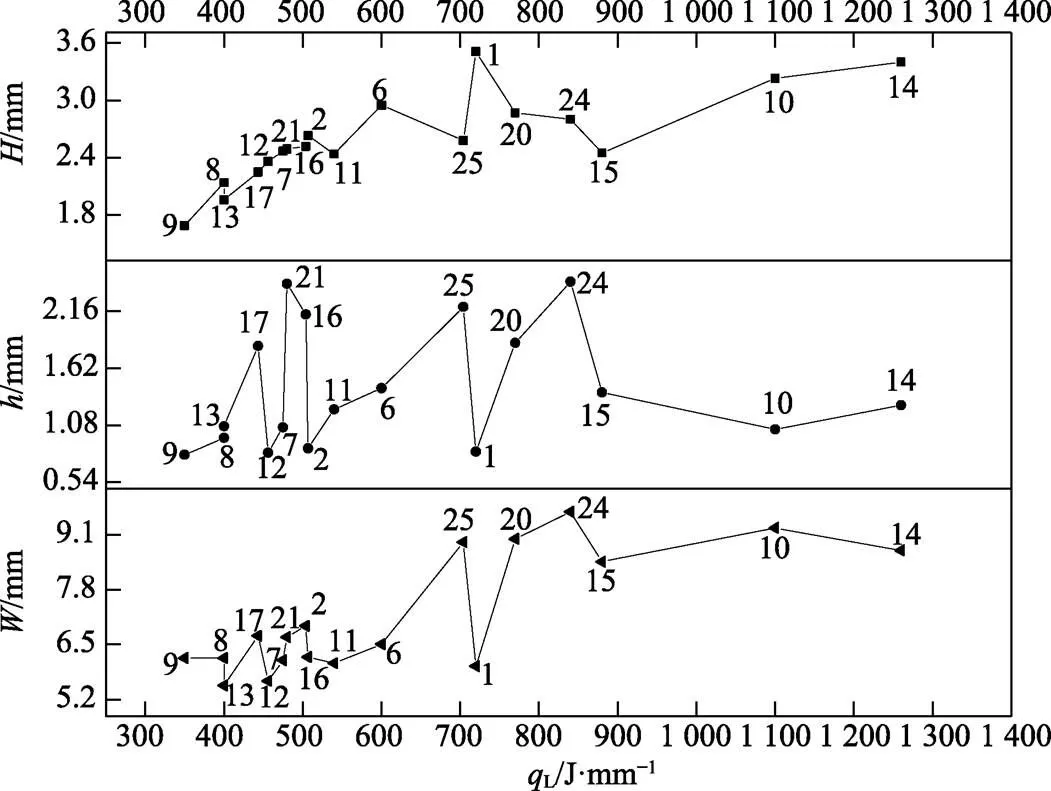
图4 线能量对增材层宽度、增材层高度及熔深的影响
由图4可知,增材层宽度随着线能量的增大有逐渐增大的趋势,但在线能量较低(约350~500 J/mm)时,增材层宽度随着线能量的增大而有较明显的波动,在线能量较高(约880 J/mm以上)时,增材层宽度基本保持稳定。增材层高度随着线能量的增大呈现出较明显的上升趋势,但上升幅度随着线能量的增大而逐渐减弱。熔深随线能量的增大而产生较大的波动,整体上无明显上升或下降的趋势,仅在线能量较高(约880 J/mm以上)时才基本趋于稳定。
2.2 增材层形貌回归预测
2.2.1 基于线能量的单变量回归预测
分别对增材层宽度、增材层高度及熔深3个结果数据与线能量L之间的关系进行线性回归分析,所得回归方程及相应2和adj2如表4所示。
表4 增材层宽度、高度及熔深与线能量的线性回归关系

Tab.4 Linear regression relationship between width, height of additive layer, and depth of weld penetration
表4中,2和adj2分别表示回归决定系数和调整后回归决定系数,二者取值均为[0, 1],2和adj2越接近1且二者越接近时表示回归效果越好,对线性回归而言,即表示回归方程中因变量和自变量之间的线性关系越明显。显然,由表4可知,、和与线能量之间的线性关系并不明显,尤其与线能量之间几乎没有任何线性关系。
同样,考虑到增材层宽度、高度随线能量的增大均呈现出逐渐增大且增速逐渐变缓的趋势,分别回归了、及与L之间的二次函数关系,如图5所示。由图中所给出的二次函数关系式及回归质量信息可知,、和L之间二次回归的2和adj2均只有0.6左右,即增材层宽度、高度与线能量之间的二次函数关系非常弱;和L之间二次回归的2和adj2分别为0.173和0.062 7,即熔深和线能量之间几乎不存在二次函数关系。

图5 增材制造形貌参数与线能量的二次函数关系
通过以上分析可知,增材层宽度、增材层高度和熔深与线能量之间的线性和二次回归结果质量均较差,难以直接用线能量来表征电弧增材制造单道成形的关键质量信息。
2.2.2 多元线性回归预测
利用多元线性回归分析可以建立增材制造工艺参数与单道成形质量参数之间的定量函数关系。多元回归方程建立的基本过程为:将电流、电压、焊枪移动速度、焊道长度作为自变量参数,将增材层宽度、增材层高度和熔深分别作为目标,建立各目标与自变量的定量化函数方程;而后检查各自变量对方程影响的显著性,如某个自变量的影响不显著(取置信度95%),则剔除该参数后重新回归直至得到最优方程。
在进行多元线性回归预测时,将18组数据划分为两部分,一部分进行回归计算建立预测方程,另一部分用于验证回归方程预测的准确性。根据线能量分布均匀的原则,选取第8、11、24这3组数据作为验证数据,其余15组用于建立回归方程。经逐步回归后可得到3个目标值与各工艺参数之间的最佳回归方程及其回归决定系数和调整后的回归决定系数,如表5所示。
表5 多元线性回归结果

Tab.5 Results of multiple linear regression
由表5中的回归方程及其回归质量参数可以看出,多元线性回归法对于增材层宽度的拟合效果较好,对于增材层高度的拟合效果次之,而对于熔深的拟合效果则较差。将第8、11、24这3个验证组的增材制造工艺参数数据代入上述回归方程中,可以得出多元回归预测的增材层宽度'、增材层高度'和熔深',并与实验实测结果进行对比,如表6所示。表中、和分别为多元回归法预测的'、'和'的误差率,负值表示预测值小于实验值。误差率计算方法如式(1)所示。

式中:为误差率;p为预测值;为实验值。误差率平均值为各误差率绝对值的均值。
由表6可知,多元回归模型对于增材层宽度的预测值较精确,且不同工艺参数下预测结果误差率波动不大,平均预测误差率仅为4.66%。但对于不同工艺参数下增材层高度和熔深的预测结果误差波动较大,例如第8组增材层高度预测误差率仅‒1.59%,但第11组达到了16.52%。同时,增材层高度和熔深预测的平均误差率均较高,分别达到了8.07%和11.79%。此外,由各拟合方程可以看出,电流、电压和焊枪移动速度3个参数均出现在增材层宽度和高度的预测方程中,即这两个参数对增材层宽度及高度产生显著的影响作用;而焊道长度在3个方程中均未出现,即焊道长度对增材层形貌的影响并不显著;对于熔深而言,仅有电流这一个参数的影响是显著的,但考虑到该方程拟合度不高,并结合焊接基本原理,认为电压和焊接速度对熔深应该有较明显的影响,但各参数间存在非线性的交互作用,导致其多元线性回归效果不佳。
表6 实验结果与多元线性回归预测结果对比

Tab.6 Comparison of experimental results and predicted results by multiple linear regression
以上分析说明,无论是基于线能量的单变量回归模型还是基于焊接电流、电压及焊枪移动速度的多元线性回归模型,均难以实现对3个增材制造形貌关键参数的准确预测。这是由于增材制造成形时,电流、电压和焊枪移动速度等工艺参数共同对焊接热源形状、热输入、焊丝和基材熔化及凝固、增材制造体系散热等产生相互耦合的影响,这些参数相互间的影响是高度非线性的,难以用常规的线性回归或高阶多项式回归方法得到增材制造工艺参数和最终成形质量参数间的关系。
2.3 增材层形貌神经网络预测
2.3.1 神经网络基本原理及预测方法
图6显示了一种典型的人工神经网络结构。人工神经网络主要由输入层、隐含层和输出层构成,每层中的圆圈称为人工神经元,其中,输入层用于接收变化的各影响因素信息,隐藏层(可以有多层)将输入层传递来的信息转换为输出层可以使用的信息,输出层则根据上一个隐含层的信息输出研究者关心的指标结果;通过不断调整各神经元之间的连接强度(即权重),最终可建立输入信息和输出指标间高精度的对应关系,实现结果预测。神经网络具有高度的非线性函数逼近能力、自适应学习能力和容错能力,因而在非线性系统建模中得到了广泛应用。
采用神经网络法进行预测的首要任务是确定神经网络结构,即确定神经网络的输入、输出和隐含层层数及每个隐含层神经元的个数。由于文中主要研究电流、电压、焊枪移动速度和焊道长度4个工艺对增材层宽度、增材层高度和熔深3个结果指标的影响,其中,通过前文的分析可知,焊道长度对3个指标的影响不显著,故可确定输入为3个参数,输出为3个结果指标,即可以建立一个3输入3输出的神经网络来一次性完成增材层宽度、增材层高度和熔深的预测。但根据神经网络原理和笔者前期试算可知,多输出的神经网络预测精度会降低,因而建立了3个3输入1输出的神经网络分别对增材层宽度、增材层高度和熔深3个指标进行预测。在神经网络中,隐含层的层数和每个隐含层的神经元个数决定了神经网络的预测精度。由于本文预测问题的复杂程度较低,因而只使用1个隐含层。隐含层神经元个数可由经验公式(式(2))计算得到[17]。
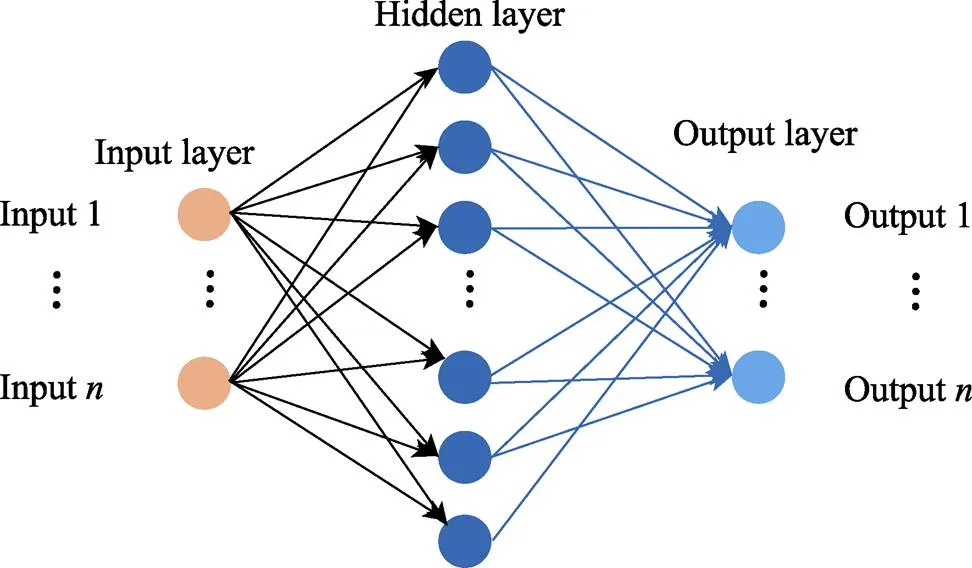
图6 神经网络结构示意图

式中:为输入神经元个数;为输出神经元个数;为[1, 10]之间的常数。通常而言,的取值需要通过多次神经网络训练并对比结果优劣来确定,但在SPSS中,软件可自动完成这一过程,根据预测指标的不同,的最终取值不同。
在确定神经网络结构后,使用SPSS软件搭建神经网络,因输入、输出数据的单位和数值量级不同,为保证各变量之间的可比性,需要对输入、输出数据进行归一化处理,此外,还需要选定隐藏层激活函数和输出层激活函数,这些过程均可在SPSS软件中自动完成。最终采用的归一化公式如式(3)所示,隐藏层激活函数和输出层激活函数分别为双曲正切函数和恒等式。
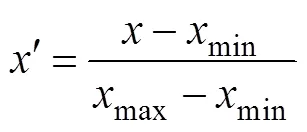
式中:'为归一化结果;为样本值;min和max分别为最小样本值和最大样本值。
与多元线性回归预测一样,第8、11、24这3组数据不参与神经网络训练,而用于检验模型最终预测效果,其余15组用于神经网络训练(在训练过程中,神经网络自动按照8:2的比例将这15组数据划分为训练集和测试集)。在训练完成后,保存网络并将第8、11、24组数据代入神经网络即可得出增材层宽度、增材层高度和熔深的神经网络预测值。由于神经网络中各神经元初始权重值是随机赋予的,因而每次神经网络训练结果均不一样,本文针对每个预测指标均进行了两次神经网络训练。
2.3.2 神经网络预测精度分析
每个指标的2次神经网络预测结果及其误差率如表7所示。由表7可知,神经网络的预测精度与其训练过程有关,不同的训练过程得出的预测结果精度差异较大,但若网络训练合理,可以得到较高精度的预测结果。在实际应用中,可多次训练神经网络,通过验证集的平均误差等指标选择预测效果最佳的网络,文中对于增材层宽度的预测选第2次训练的网络,对于增材层高度和熔深则均取第1次训练的网络,3个参数的预测平均误差率分别为4.17%、6.60%和7.01%。
表7 实验结果与神经网络预测结果对比

Tab.7 Comparison of experimental results and predicted results by neural network
Note: Subscript "1" represents the first neural network prediction training; subscript "2" represents the second neural network prediction training.
为了进一步对比神经网络与多元回归法对于增材制造单道成形形貌预测效果的好坏,将两种方法对于验证组预测结果的误差率绘制在同一幅图中,如图7所示。由图7可知,对于增材层宽度而言,2种方法的预测精度均较高,平均误差率均在5%以内,神经网络针对不同组别的预测结果误差波动较大,对于部分组别的预测误差大于多元线性回归(如第8组),但整体而言,神经网络预测精度更高。这是由于增材层宽度的变化与焊接电流、电压和焊枪移动速度之间有较好的多元线性关系(由表5中的回归方程可以看出),而神经网络对于多元线性关系同样能进行很好的预测,且其精度更高。
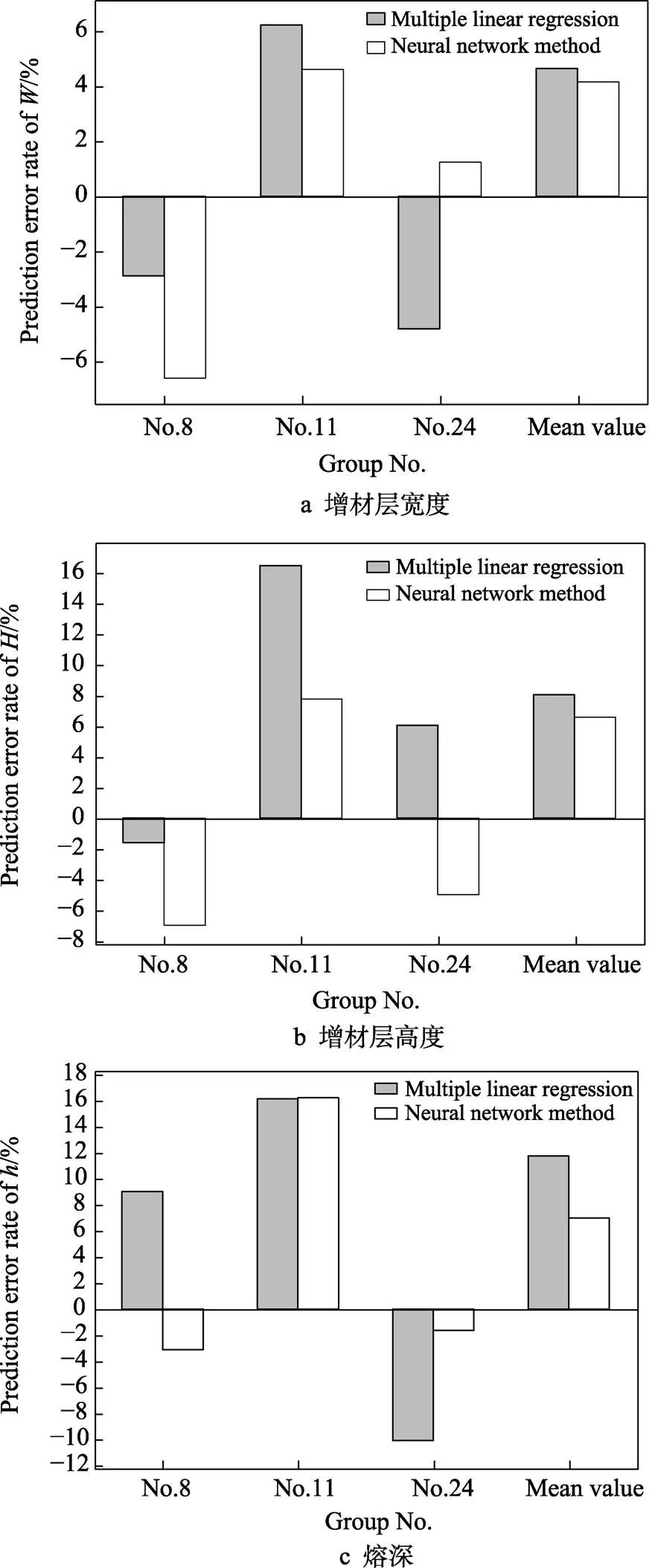
图7 预测结果误差率对比
对于熔深而言,神经网络对于第8组和第24组的预测误差率均明显低于多元线性回归,神经网络的预测平均误差率为7.01%,而多元线性回归预测的平均误差率达到11.79%,神经网络的预测精度显著高于多元线性回归。这是由于熔深的变化与除电流之外的其他参数之间的线性关系不明显,而是受到各参数间较复杂的非线性交互作用的影响,因而多元线性回归法不能很好地进行预测,但神经网络法却可以准确、高效地处理非线性交互作用,预测结果更加精确。同样,对于增材层高度而言,由于焊接电流、电压和速度的交互作用会对熔滴的流动性、铺展性等产生较复杂的影响,因而多元线性回归法对于不同组别的预测结果精度差异很大,而神经网络法对于不同组别的预测结果精度稳定性较好,且平均预测误差明显低于多元线性回归。
总体而言,神经网络法对于增材制造单道成形形貌预测具有更高的精度,且由于神经网络的特性,当参与训练的数据记录越多时,神经网络的预测精度将更高。此外,神经网络相较于多元线性回归还可以接受更多的输入,即考虑更多工艺参数的影响。在实际生产中,可以通过部分实验结果训练建立工艺参数与单道成形形貌指标间的神经网络,随着生产的进行,可将得到的结果进一步送入神经网络进行训练以优化其性能,最终实现工艺参数的选取、优化和生产结果的精确预测。
3 结论
1)电弧增材制造单道成形形貌与焊接电流、电压和焊枪移动速度显著相关,单道焊接长度对成形形貌的影响不显著;各参数间存在非线性交互作用,焊接线能量与成形形貌各指标间没有明显的线性或二次相关关系。
2)单道增材层宽度与焊接电流、电压和焊枪移动速度间存在明显的多元线性关系,采用多元线性回归法可较准确地预测单道增材层宽度(平均预测误差率仅为4.66%),但对于增材层高度和熔深的预测效果较差(平均误差率分别为8.07%和11.79%)。
3)神经网络可良好地处理各工艺参数间复杂的非线性关系,其对于增材层宽度、增材层高度和熔深的预测平均误差率分别为4.17%、6.60%和7.01%,显著高于多元线性回归法;采用神经网络法可以准确预测电弧增材制造单道成形的形貌参数,进而指导增材制造工艺参数的选取和成形质量的控制。
[1] 石玗, 朱珍文, 张刚, 等. 金属电弧增材成形控制关键技术及研究现状[J]. 材料导报, 2022, 36(12): 135-142.
SHI Yu, ZHU Zhen-wen, ZHANG Gang, et al. Key Technology and Status of Metal Arc Additive Morphology Control[J]. Materials Reports, 2022, 36(12): 135-142.
[2] WANG Ting-ting, ZHANG Yuan-bin, WU Zhi-hong, et al. Microstructure and Properties of Die Steel Fabricated by WAAM Using H13 Wire[J]. Vacuum, 2018, 149: 185-189.
[3] LIU Zhi-yuan, ZHAO Dan-dan, WANG Pei, et al. Additive Manufacturing of Metals: Microstructure Evolution and Multistage Control[J]. Journal of Materials Science & Technology, 2022, 100: 224-236.
[4] 姜淑馨, 李峰光. 丝材电弧增材制造技术的研究与应用[J]. 铸造技术, 2022, 43(5): 369-374.
JIANG Shu-xin, LI Feng-guang. Research and Application of Wire and Arc Additive Manufacturing Technology[J]. Foundry Technology, 2022, 43(5): 369-374.
[5] 王华明. 高性能大型金属构件激光增材制造: 若干材料基础问题[J]. 航空学报, 2014, 35(10): 2690-2698.
WANG Hua-ming. Materials' Fundamental Issues of Laser Additive Manufacturing for High-Performance Large Metallic Components[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(10): 2690-2698.
[6] SINGH S, SHARMA S K, RATHOD D W. A Review on Process Planning Strategies and Challenges of WAAM[J]. Materials Today: Proceedings, 2021, 47: 6564-6575.
[7] 卢秉恒. 增材制造技术——现状与未来[J]. 中国机械工程, 2020, 31(1): 19-23.
LU Bing-heng. Additive Manufacturing—Current Situation and Future[J]. China Mechanical Engineering, 2020, 31(1): 19-23.
[8] 张金田, 王杏华, 王涛, 等. 电弧增材制造单道单层工艺特性研究[J]. 材料导报, 2020, 34(24): 24132- 24137.
ZHANG Jin-tian, WANG Xing-hua, WANG Tao, et al. Study on the Processing Characteristics of Single-Bead and Single-Layer in the WAAM[J]. Materials Reports, 2020, 34(24): 24132-24137.
[9] DEREKAR K S. A Review of Wire Arc Additive Manufacturing and Advances in Wire Arc Additive Manufacturing of Aluminium[J]. Materials Science and Technology, 2018, 34(8): 895-916.
[10] 许剑. 药芯丝材脉冲TIG电弧增材制造工艺及数值模拟研究[D]. 天津: 天津理工大学, 2021: 21-28.
XU Jian. Research on Process and Numerical Simulation of Flux Cored Wire and Pulsed TIG Arc Additive Manufacturing[D]. Tianjin: Tianjin University of Technology, 2021: 21-28.
[11] LI Kun, KLECKA M A, CHEN Shu-ying, et al. Wire-Arc Additive Manufacturing and Post-Heat Treatment Optimization on Microstructure and Mechanical Properties of Grade 91 Steel[J]. Additive Manufacturing, 2021, 37: 101734.
[12] KUMAR A, MAJI K. Numerical and Experimental Investigations on Deposition of Stainless Steel in Wire Arc Additive Manufacturing[J]. International Journal of Manufacturing, Materials, and Mechanical Engineering, 2021, 11(4): 40-56.
[13] 姜淑馨, 李峰光. 工艺参数对H13钢电弧增材制造成形品质的影响[J]. 特种铸造及有色合金, 2022, 42(5): 642-646.
JIANG Shu-xin, LI Feng-guang. Influence of Process Parameters on Forming Quality of H13 Steel by WAAM[J]. Special Casting & Nonferrous Alloys, 2022, 42(5): 642-646.
[14] 梁旭东, 王炜, 赵凯, 等. 随机森林回归分析在激光熔覆形貌预测中的应用[J]. 中国有色金属学报, 2020, 30(7): 1644-1652.
LIANG Xu-dong, WANG Wei, ZHAO Kai, et al. Application of Random Forest Regression Analysis in Trace Geometry Prediction of Laser Cladding[J]. The Chinese Journal of Nonferrous Metals, 2020, 30(7): 1644-1652.
[15] YANG Yang, CAO Long-chao, ZHOU Qi, et al. Multi-Objective Process Parameters Optimization of Laser-Magnetic Hybrid Welding Combining Kriging and NSGA-II[J]. Robotics and Computer-Integrated Manufacturing, 2018, 49: 253-262.
[16] 温海骏, 孟小玲, 许向川, 等. 基于神经网络和遗传算法的激光熔覆工艺参数多目标优化[J]. 应用激光, 2019, 39(5): 734-740.
WEN Hai-jun, MENG Xiao-ling, XU Xiang-chuan, et al. Multi-Objective Optimization of Laser Cladding Process Parameters Based on Neural Network and Genetic Algorithm[J]. Applied Laser, 2019, 39(5): 734-740.
[17] 范鹏飞, 张冠. 基于线性回归和神经网络的金属陶瓷激光熔覆层形貌预测[J]. 表面技术, 2019, 48(12): 353-359, 368.
FAN Peng-fei, ZHANG Guan. Prediction on Geometrical Characteristics of Cermet Laser Cladding Based on Linear Regression and Neural Network[J]. Surface Technology, 2019, 48(12): 353-359, 368.
[18] LE Xia-wei, HAO Jing-bin, MENG Qing-dong, et al. Prediction of 18Ni300 Laser Cladding Topography Based on Back-Propagation Neural Network and Particle Swarm Optimization[J]. Journal of Physics: Conference Series, 2021, 1775(1): 012009.
[19] LIU J C, NI L B. Prediction of Laser Clad Parameters Based on Neural Network[J]. Materials Technology, 2012, 27(1): 11-14.
[20] 刘干成, 黄博. 基于GA-BP神经网络的镍基合金熔覆涂层形貌预测[J]. 应用激光, 2018, 38(4): 527-535.
LIU Gan-cheng, HUANG Bo. Prediction of Ni-Based Alloy Cladding Coatings Topography Based on GA-BP Neural Network[J]. Applied Laser, 2018, 38(4): 527- 535.
[21] 吴许祥, 王成, 薛华军, 等. 基于BP神经网络的激光焊接工艺参数优化及组织性能研究[J]. 锻压装备与制造技术, 2021, 56(6): 77-82.
WU Xu-xiang, WANG Cheng, XUE Hua-jun, et al. Research on Optimization of Laser Welding Process Parameters and Microstructure Performance Based on BP Neural Network[J]. China Metalforming Equipment & Manufacturing Technology, 2021, 56(6): 77-82.
[22] 康靓, 米晓希, 王海莲, 等. 人工神经网络在材料科学中的研究进展[J]. 材料导报, 2020, 34(21): 21172- 21179.
KANG Jing, MI Xiao-xi, WANG Hai-lian, et al. Research Progress of Artificial Neural Networks in Material Science[J]. Materials Reports, 2020, 34(21): 21172-21179.
[23] 米晓希, 汤爱涛, 朱雨晨, 等. 机器学习技术在材料科学领域中的应用进展[J]. 材料导报, 2021, 35(15): 15115-15124.
MI Xiao-xi, TANG Ai-tao, ZHU Yu-chen, et al. Research Progress of Machine Learning in Material Science[J]. Materials Reports, 2021, 35(15): 15115-15124.
[24] RAMPRASAD R, BATRA R, PILANIA G, et al. Machine Learning in Materials Informatics: Recent Applications and Prospects[J]. Npj Computational Materials, 2017, 3: 54.
[25] XU Jian-ning, ZHANG Hua, ZHANG Guang-yun, et al. The Choice of Welding Parameters and Prediction of Weld Seam Dimensions for Welding Rapid Prototyping[C]//2008 IEEE Conference on Cybernetics and Intelligent Systems. Chengdu, China: IEEE, 2008: 976-979.
[26] XIONG Jun, LI Yan-jiang, YIN Zi-qiu, et al. Determination of Surface Roughness in Wire and Arc Additive Manufacturing Based on Laser Vision Sensing[J]. Chinese Journal of Mechanical Engineering, 2018, 31(1): 74.
[27] XIONG Jun, YIN Zi-qiu, ZHANG Wei-hua. Forming Appearance Control of Arc Striking and Extinguishing Area in Multi-Layer Single-Pass GMAW-Based Additive Manufacturing[J]. The International Journal of Advanced Manufacturing Technology, 2016, 87(1): 579-586.
[28] 刘洋. H13钢汽车热锻模具激光仿生强化工艺研究[D]. 十堰: 湖北汽车工业学院, 2021: 21-23.
LIU Yang. Research on the Laser Bionic Strengthening Process of H13 Steel Automobile Hot Forging Die[D]. Shiyan: Hubei University of Automotive Technology, 2021: 21-23.
Prediction of Single-pass Arc Additive Manufacturing Forming Morphology Based on Regression and Neural Network
LI Feng-guang1, CAO Yi-fa1, GUO Rui1, JIANG Shu-xin1, LIU Jian-yong1, HU Sheng-bo1, RONG Bo-chuan2
(1. School of Materials Science and Engineering, Hubei University of Automotive Technology, Hubei Shiyan 442002, China; 2. No.1 Mechanical and Electrical Office of Beijing Fangshan District Special Equipment Testing Institute, Beijing 102401, China)
The work aims to determine an efficient and accurate mathematical method for predicting the forming morphology of single pass in arc additive manufacturing to solve the difficulties in selecting process parameters and predicting forming results in practical application of arc additive manufacturing technology, so as to select the process parameters of wire arc additive manufacturing quickly and conveniently and guide the forming quality control. A variety of regression methods and neural network methods were used to establish the mathematical relationship model between the multiple process parameters (welding current, voltage, welding torch moving speed, et al) and forming morphology parameters (width of additive layer, height of additive layer and depth of weld penetration) based on the single-pass single-layer wire arc additive manufacturing experiment. The results showed that the single-pass forming morphology of arc additive manufacturing was significantly related to welding current, voltage and moving speed of welding torch, and nonlinear interaction existed between the parameters. The multiple linear regression method could accurately predict the width of single additive layer, but the prediction effect of additive layer height and weld penetration depth was poor. The neural network could handle the complex nonlinear relationship among the process parameters well, its average prediction error rates on the width, height and penetration of the additive layer were respectively 4.17%, 6.60% and 7.01%, which were significantly lower than those of the multiple linear regression method. The neural network method can accurately predict the morphology parameters of arc additive manufacturing single-pass forming, and then guide the selection of additive manufacturing process parameters and the control of forming quality.
arc additive manufacturing; forming morphology; neural network; H13 steel;regression method
10.3969/j.issn.1674-6457.2023.02.020
TG44
A
1674-6457(2023)02-0171-09
2022‒07‒28
2022-07-28
国家自然科学基金(51604103);湖北省教育厅科研计划重点项目(D20221801);湖北省教育厅科研计划(Q20211804);湖北汽车工业学院“增材制造及表面强化”校级创新团队(B05)
National Natural Science Foundation of China (51604103); Key Scientific Research Project of Education Department of Hubei Province (D20221801); Scientific Research Project of Education Department of Hubei Province (Q20211804); Innovation Team Found of Hubei University of Automotive Technology: Additive Manufacturing and Surface Strengthening (B05)
李峰光(1987—),男,博士,教授,主要研究方向为增材制造、激光表面强化。
LI Feng-guang (1987-), Male, Doctor, Professor, Research focus: additive manufacturing and laser surface strengthening.
郭睿(1989—),男,硕士,讲师,主要研究方向为增材制造、铸造工艺优化。
GUO Rui (1989-), Male, Master, Lecturer, Research focus: additive manufacturing and casting process optimization.
李峰光, 曹宜发, 郭睿, 等. 基于回归方法和神经网络的电弧增材制造单道成形形貌预测[J]. 精密成形工程, 2023, 15(2): 171-179.
LI Feng-guang, CAO Yi-fa, GUO Rui, et al. Prediction of Single-pass Arc Additive Manufacturing Forming Morphology Based on Regression and Neural Network[J]. Journal of Netshape Forming Engineering, 2023, 15(2): 171-179.

