基于混合核函数GA-SVR的动车组制动闸片寿命预测

毛嘉伟，李永华，王佳楠，胡超群

(大连交通大学 机车车辆工程学院，辽宁 大连 116028)

动车组制动闸片作为基础制动装置的关键部件，其健康状态直接决定着制动系统能否正常运转。在运用过程中，制动闸片绝大多数失效都由摩擦磨损引起，因而对于制动闸片进行寿命预测的主要工作就是能够准确预测闸片在不同运用时期的实际厚度[1]。在统计学模型和物理模型方面，李宏伟等[2]通过观测及研究350 km/h标准动车组制动闸片在实际服役条件下的磨损行为，采用曲线拟合的方式对其进行了使用寿命的初步预测。王娴等[3]针对磨耗数据采用Kalman滤波方法预测闸片剩余寿命，并通过实例验证了该方法的有效性。张一喆等[4]建立了三参数威布尔寿命分布模型，对制动闸片的寿命进行评估的同时也对后续检修更换周期做出了讨论。这2类预测方法为保证预测精确度对研究对象试验数据的准确性要求极高且适用范围受限，并非当今主流方式。近年来，人工智能、机器学习和数据挖掘等领域相关理论与技术已经愈发成熟，基于数据驱动的智能算法已被广泛用于寿命预测领域。DUC等[5]为克服基于物理模型预测对制造以及监测环境的强烈依赖性，采用决策树以及随机森林算法对刹车片的剩余寿命进行预测。FENG等[6]采用了神经网络及灰色理论对动车组制动闸片的寿命进行预测。然而神经网络方法对于小样本以及高维度数据的处理上存在着泛化能力差，收敛速度慢等问题。支持向量机(Support Vector Machines, SVM)克服了神经网络方法在小样本寿命预测中存在的一系列问题，且具有较高的预测精确度以及良好的泛化能力，在寿命预测领域应用逐渐广泛[7]。但值得一提的是，SVM关键参数的选取对模型的性能有着绝对的影响，是提高寿命预测精确度最为关键的一步。为进一步提高SVM模型的分类及回归性能，LAREF等[8]对SVM中每个超参数对模型性能的影响进行了分析，并提出了一种广义模式搜索法GPSM(Generalized Potential Search, Method)来提升网格搜索算法对超参数寻优求解的效率。SU等[9]为进一步优化SVM核参数，提高模型分类效率，提出了一种改进的粒子群算法，有效解决了小样本情况下风电机组系统故障难以识别问题。HWEJU等[10]提出了精细化高斯SVR模型，预测精度高于传统的线性回归SVR模型，实现了在小样本情况下对车床表面粗糙度的精确预测。陈伟根等[11]建立了基于GA-SVR的变压器绕组热点温度预测模型，并证明该模型的预测结果与实验结果基本一致，在预测精度上优于Elman神经网络方法。目前基于SVM的寿命预测研究方面，主要通过寻找最优单个核函数或者通过智能算法优化核参数来提高分类或回归预测的准确率，但同样存在不能兼顾SVM核矩阵结构的改进以及核参数最优化的问题，仍具有一定的局限性[12]。为了更好地提高SVM方法的预测精度，本文考虑SVM中全局核函数与局部核函数特点，并采用遗传算法对核参数进行寻优求解，建立一种采用混合核函数的GA-SVR回归模型应用于动车组制动闸片的寿命预测。结果表明，该模型的预测精度以及泛化能力上相比于单核模型都有所提高，体现了所述模型的有效性。

1 混合核函数矩阵的构建

1.1 核函数及其性质

SVM模型中核函数的选取对模型的分类效果、回归精度及泛化能力等许多特性具有决定性的作用。但不同类型的核函数作用概括来说分为2点：第一，将低维空间的样本映射到高维特征空间，从而进行数据类别划分，得出变量之间的非线性关系。第二，使得样本之间在空间中的内积运算维数降低，极大简化计算量。常见的核函数有以多项式核函数和径向基核函数为代表的2类[13]。

1) 多项式核函数：

多项式函数是一种典型的全局核函数，函数曲线图如图1所示，在与测试点x=0.1相距很远的样本点依然能对核函数取值产生较大影响，因而便于提取样本信息总体特征，有良好的外推能力。

图1 多项式核函数特性曲线图Fig. 1 Characteristic curves of polynomial kernel function

2) 径向基核函数：

径向基函数是一种典型的局部核函数，具有优秀的局部插值能力。函数曲线图如图2所示。测试点x=0.2附近区域核函数取值不为0，随着距离的增加，核函数值几乎为0。因而便于提取样本的局部特性，有着卓越的学习能力。

图2 径向基核函数特性曲线图Fig. 2 Characteristic curve of radial basis kernel function

1.2 混合核函数SVR回归模型的建立

单一核函数模型在对非线性样本进行高维空间映射时往往具有一定的局限性，因此经过训练得到映射空间的特征分布与实际情况均存在不同类型的偏差。因此即便是对核参数进行优化后，得到的也不尽是精确的预测结果。RBF核函数学习能力极强，通过合理的设置参数便可用于服从任意分布的样本回归预测。多项式核函数的推广能力极强，项的次数越低，推广性越强。因此本节通过考虑局部以及全局核函数的各自优点，构造一种结合多项式核函数与RBF核函数特性的混合核函数代替单个核函数，应用到寿命预测之中进一步提高回归预测的准确率。

核函数的组合方式有很多种，均要满足Mercer条件[14]。本文构建了一种基于Mercer条件的混合核函数的支持向量机。为保证一定的泛化能力并尽可能降低计算复杂度，多项式核函数的次数为2次，具体组合形式为式(3)。

式中：参数λ是调节多项式核函数和RBF核函数特性占比的常数，取值范围为[0, 2][15]。而通过大量的试验可以确定，λ一般取0.25～1.99，且当λ取值较大时(经验证本文为1.75)，融合的性能最佳。混合后核函数曲线图如图3所示。

图3 混合核函数特性曲线图Fig. 3 Characteristic curves of mixed kernel function

混合后的核函数能够同时体现样本的总体及局部特征，给定合适维度的输入样本，经过核函数的映射及模型自身的学习，可以得出相匹配的SVR回归决策函数。

2 基于遗传算法的模型性能改进

2.1 模型优化流程

采用SVR回归模型进行预测时需要调节关键参数才能使其具有最佳性能。本文主要针对核函数中的惩罚参数c以及核函数参数g进行优化。惩罚参数c的大小代表着对模型误差大于ε样本的惩罚力度，核函数参数g的大小决定着模型局域宽度以及边界的复杂程度。

交叉验证(Cross-Validation, CV)是一种应用于验证分类器性能的统计学方法，能够有效避免模型过学习和欠学习现象的发生[16]。而遗传算法(Genetic Algorithm, GA)是一种全局搜索以及优化算法，以适应度来模拟个体的生存几率。有着全局搜索以及迭代速度快优点[17]。因而将二者结合可以有效地对模型所选参数进行优化，提升回归预测精确度。选取的评价指标通常为均方误差Mse以及平方相关系数R2。

本文中对SVR回归模型进行参数优化的基本步骤如下：

1) 确定优化参数，并对其进行编码，设定寻优的初始范围；

2) 生成初始群体，随机产生个体，并设定遗传算法的相关参数；

3) 在K-CV方法的意义下以Mse和R²为评价标准计算适应度验证分类准确率；

4) 选择、交叉、变异；

5) 终止条件判断：满足迭代次数或解收敛则进行解码并输出最优结果，否则重复第2步继续进行。

2.2 基于遗传算法的模型参数优化结果

为获得最优模型参数，需对遗传算法中的初始参数以及优化参数取值范围进行预设值，并给定合适的交叉验证次数，以保证在避开繁重的计算量的同时得到可信的最优解。本节首先给出基于遗传算法优化SVR模型参数的数学模型设计优化三要素选择，优化设计的数学模型通常为式(4)。

式中：z为目标函数，在本文中为CV交叉验证方法下产生累计均方误差和的最小值。h(x,y)和g(x,y)分别为等式不等式约束，本文均为不等式约束，分别为约束单次交叉验证产生的Mse值小于1×10-4，以及迭代的最大次数小于给定的代数。设计变量为模型的惩罚因子c以及核函数带宽g，变量空间及遗传算法中各参数设置见表1。

依照表1参数设置方式分别对多项式核函数、RBF核函数构成的模型进行K-CV意义下的参数优化，得到的c/g寻优算法的适应度变化曲线分别如图4和图5所示。

图4 多项式核函数c/g参数适应度变化曲线Fig. 4 Polynomial kernel function c/g parameter evolution iterative process

图5 RBF核函数c/g参数适应度变化曲线Fig. 5 RBF kernel function c/g parameter evolution iterative process

在K=5时的CV交叉验证方法下，通过遗传算法优化获得的2种核函数SVR模型的最佳惩罚因子Bestc，最佳核函数带宽Bestg的取值以及Mse值见表2。

表2 2种核函数的最佳参数及均方误差值Table 2 Optimal parameters and mean square error of the two kernel functions

由此便通过遗传算法确定了以多项式函数以及RBF函数为主体的2个单核性能最佳的SVR回归模型，进而采用式(3)的方式对得到的最优模型的单核矩阵进行融合便得到混合核GA-SVR模型用于后续的寿命预测。相关流程如图6所示。

图6 基于混合核GA-SVR模型寿命预测流程Fig. 6 Flow chart of hybrid core GA-SVR model life prediction

3 工程实例-动车组制动闸片剩余寿命预测

3.1 动车组制动闸片寿命预测可行性分析与数据前处理

在实际运用过程中，闸片的厚度都是基于有限时间内测量得到的，通常间隔一段时间对其进行一次性能检测，因而该类预测属于小样本预测事件。SVR最主要优势在于处理小样本回归问题时具有传统算法无法解决的抗干扰能力，且使用RBF核函数的SVR模型在解决样本总数与特征数相差不大的问题中具有卓群的效果。因而准确地选取出能够表征闸片在运用时磨损情况的相关特征变量作为输入，以闸片实际厚度作为输出变量，通过SVR模型进行回归预测是基于摩擦磨损原理进行预测的外另一种准确可行的预测方法。

在分析制动闸片磨损块厚度变化对动车组制动性能的影响时可以发现，随着磨损块的不断损耗，闸片的摩擦因数会不断降低，与轮对的接触性能会有所下降，进而导致采取止动后列车的实际制动距离会不断增加、制动时间不断延长。直观的表现就是在摩擦产生的温升现象更加严重，导致磨损块表面温度不断剧烈升高，这些特性是反映闸片性能的重要因素。选取RBF核函数可以有效识别这些输入变量的变化对输出变量的影响，准确地提取特性。多项式核函数在此基础上能够提高模型的泛化能力，即便样本个数较大，也能准确表征出磨损特征，在大小样本上都能体现出一定的适用性，表明了采用机器学习方法进行闸片寿命预测的先进性。

选取某项目动车组制动闸片作为研究对象，每月同一时刻对磨损块厚度进行实测[3]，并对其上述制动性能参数也加以监测，连续采集一定时间得到的部分数据见表3。其中实际制动距离代表列车开始空气制动时闸片的磨损块作用于轮对开始到停止所走行的实际距离，对应的时间为实际制动时间。在200 km/h的速度下制动最大距离不应超过2 000 m。表面最高温度即进行空气制动时闸片与轮对摩擦造成的温升，最高温度不应超过600 ℃。摩擦因数是磨损块与轮对之间的摩擦力与正压力的比值，其值越大便表明二者间产生的

表3 制动闸片厚度及制动特性测量数据Table 3 Brake disc thickness and brake characteristics measurement data

有效摩擦力越大，在一般情况下取值通常为0.25～0.5。

选取数据中的第1列作为回归预测的输出指标，后4列作为输入特征，构成模型的核矩阵参数。由于各个输入特征间的数量级相差较大，直接对其进行训练并进行模型的建立会导致模型性能不够理想，通常为消除这种影响要对其进行归一化处理。区间选取上[0, 1]反映的是样本的概率分布，[-1, 1]则更多地反映样本的状态分布或坐标分布，因此本文归一化的区间上选取[-1, 1]，处理方式为式(5)。

式中：x为输入样本，xmin和xmax分别为输入样本中的最小值和最大值，xnew为归一化后的输入特征。部分归一化后的数据见表4。

表4 归一化后的测量数据Table 4 Normalized measurement data

其中极值-1和1分别代表闸片在实际运行中的健康状态，具体表现在实际制动距离的不断增大、制动时间的逐渐提高、盘面温度的不断升高以及摩擦因数的降低。因此归一化后相比于实际数据既能反映出真实运行状态，又能有效消除数量级的差异对模型性能的影响。选取以上归一化后的50组数据作为训练集，用于混合核函数模型的学习与建立，选取2组同一型号的闸片在不同起始记录时期的运行时的实测数据作为训练集，用于进行使用寿命的预测，将得到的结果与单核模型的对其进行寿命预测的预测结果进行对比，体现本文所提出的模型与单一核函数模型的优越性。

3.2 动车组制动闸片剩余寿命预测结果分析

采用50组测得的某项目动车组制动闸片全周期磨损数据作为模型的训练集，选取同一型号的闸片在2个不同部分运用周期内的18组厚度变化数据作为预测集，基于混合核函数预测模型进行寿命预测与模型精度检验。在采用训练集数据进行模型训练时，选择训练时产生的相对误差作为模型性能判定指标，分别得到了单一RBF核函数以及混合核函数模型在训练时产生的误差结果，如图7和图8所示。

图7 RBF核函数训练集相对误差图Fig. 7 RBF kernel function training set relative error chart

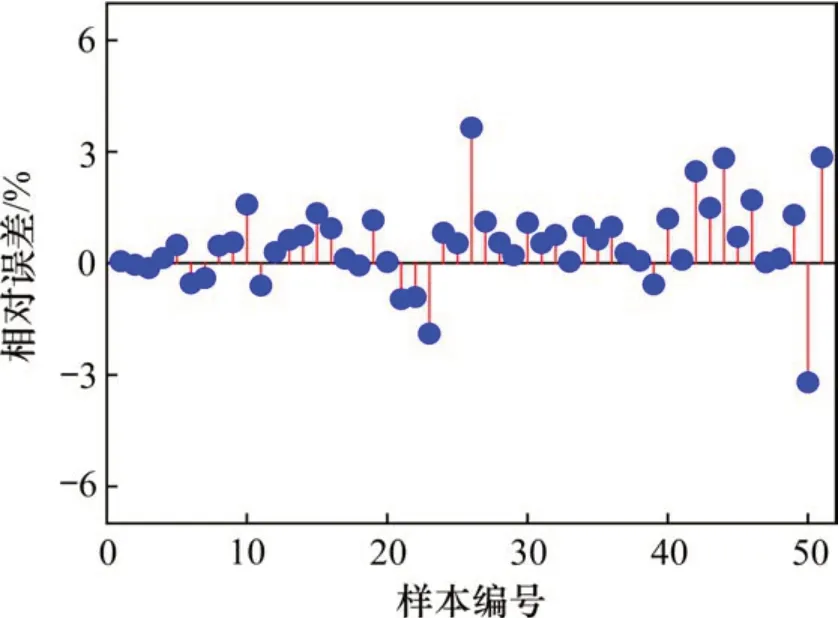
图8 混合核函数训练集相对误差图Fig. 8 Mixed kernel training set error relative chart

从图7和图8中可看出混合核方法误差整体上更低，局部误差过大的现象得到了明显的改善，累积相对误差较单一RBF核方法相比降低了8.85%。在预测相对误差数值波动上更加平稳，方差比单一RBF核方法降低了11.20%，这也体现了模型泛化的能力上有了一定的提升。在保证了一定的拟合度(0.95)前提下，2个模型的Mse值分别为1.27×10-4和1.24×10-4，从模型评价指标上也体现了混合核函数作用下的SVR模型预测精确度更高。为进一步验证该模型的实际预测精度，选取同一型号的制动闸片，以2个不同起始记录时刻(分别以a和b时段指代)得到的闸片厚度实测数据作为预测集进行预测，与RBF单核方法得到的制动闸片寿命预测结果进行对比，结果如图9～12所示。

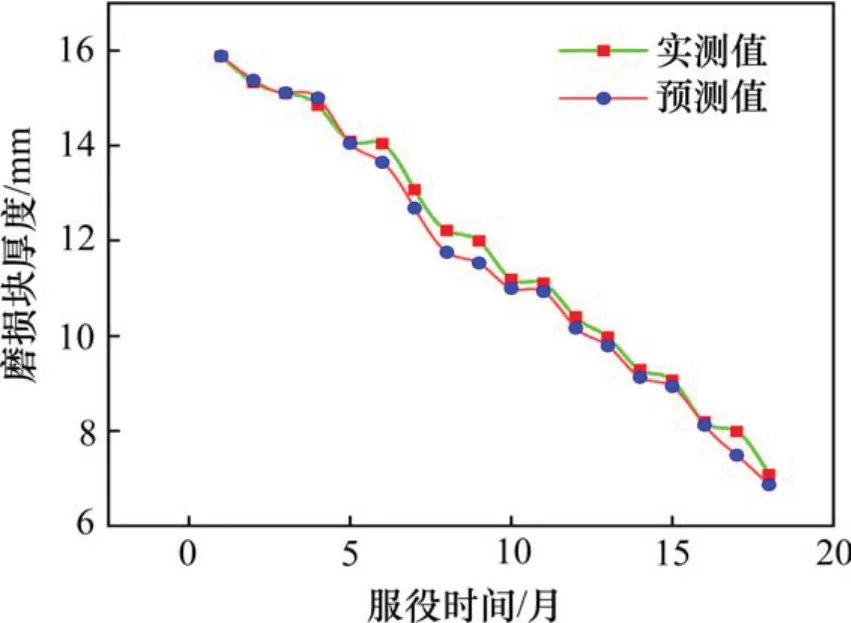
图9 a时段制动闸片寿命预测结果(RBF)Fig. 9 Brake disc life prediction results in period a (RBF)

图10 a时段制动闸片寿命预测结果(混合核)Fig. 10 Brake disc life prediction results in period a

从a和b 2个不同起始记录时段预测的结果上可以看出经过GA算法优化的RBF单核方法与混合核函数方法进行预测所得到的结果都具有良好的效果，预测得到的制动闸片磨损曲线与实际测得的磨损曲线趋势基本一致，体现了采用小样本机器学习方法进行闸片寿命预测的准确与可行性。但从整体来看在服役前中期，显然混合核方法的预测结果与实际值的近似程度均更高，克服了RBF核方法存在的局部性能不稳定的问题，定性地说明了本文模型的泛化能力有了提高。为定量得出混合核方法在精度上的优越性，对不同预测周期内采用2种方法得到的相对误差分别进行了对比，得到的结果如图13和图14所示。

图11 b时段制动闸片寿命预测结果(RBF)Fig. 11 Brake disc life prediction results in period b (RBF)

图12 b时段制动闸片寿命预测结果(混合核)Fig. 12 Brake disc life prediction results in period b

图13 a时段制动闸片寿命预测相对误差图Fig. 13 Brake disc life prediction relative error chart in period a (RBF)

图14 b时段制动闸片寿命预测相对误差图Fig. 14 Brake disc life prediction relative error chartin period b

从得到的相对误差对比来看，2种方法给出的寿命预测结果都显得相对保守。由于2个单核模型经过遗传算法优化后得到的惩罚因子c均较大，对于出错样本的惩罚力度较强，因而得到的预测值绝大部分会向上逼近真实值。相对误差值大多为负，说明预测的厚度磨损情况要比实际更为严重，即在一定的服役时间内，预测的闸片厚度要低于实际厚度，在实际运用上有利于及早预警。在累积相对误差对比上，混合核方法相比于单一RBF核方法分别降低了45.23%和34.29%，相对误差值的方差上降低了76.23%和44.21%，可见在不同预测集上，模型准确性与稳定性都有了较大的提高，体现了本文方法的合理性以及一定的普适性。

4 结论

1) 采用遗传算法以训练误差和为适应度函数分别对RBF和多项式单一核核函数的SVR回归模型进行参数优化，分别确定了2个单一核函数模型的最佳c/g值，得到最优单核模型。

2) 融合核矩阵，建立混合核函数GA-SVR回归模型，并用其对动车组制动闸片的寿命进行预测，将得到的结果与实际寿命以及采用RBF单核的GA-SVR模型预测结果进行对比，保证了足够的拟合精度(0.99以上)情况下，采用本文提出方法在2个运用时段进行预测的累计相对误差相较单核方法分别降低了45.23%和34.29%，直观表明了混合核函数方法具有更高的预测精度。

3) 从预测的误差趋势来看，采用本文提出方法在2个运用时段内得到相对误差的方差相比于单核方法分别降低了76.23%和44.21%，说明采用混合核函数方法预测产生的误差在数值整体波动更加平稳，模型的泛化能力有了提高，为提高动车组制动闸片剩余寿命的准确性提供了一定的实际参考价值。