高考英语中“七选五”的题型为什么不能“蒙”

林国红

(广东省佛山市乐从中学)

1 问题的提出

高考英语中有一类“七选五”的试题,该题一般出现在试卷阅读部分的第二节,是一篇缺少5个句子的文章,提供7 个选项,要求学生根据文章的结构、内容,从文后的7个选项中选出5个最佳选项填入文中相应空白处,使文章完整、连贯通顺.“七选五”试题中有2个多余选项(干扰选项),这类题既考查词汇、语法和语篇知识,又考查分析、归纳和推理等思维能力,对学生来说有较大的挑战性与难度.

在做“七选五”题时,若通过蒙题的方式做题,能做对多少题? 平均得分又是多少?

注:所谓的“蒙”题,是指这篇文章完全看不懂(或不看文章内容),在5个空白处随便填入一个选项.

2 问题的数学化

“七选五”试题共有5道选择题,给出7个选项,其中有2项是干扰项,学生从中选择5项依次填入每道题中,每题只有一个正确选项.从数学的角度来说,就是从7个元素中取出5个的一个排列.学生对5道题全部随机作答,记其答对的题数为X,求X的分布列与数学期望.下面利用数学中的计数原理及概率的相关知识,来说明“七选五”试题为什么不能蒙.

3 第一种蒙题方式的分析

在“七选五”试题中,每题只有一个正确选项,若不考虑同一选项被多次选择的情况,对5道题全部随机作答,记答对的题数为X,求X 的分布列与数学期望.

3.1 问题的思路分析

不妨假设正确答案为ABCDE,假设某学生答对3道题,那么可以先锁定他答对的3道题(如ABCXX,其中XX 表示两个答错的选项),有种情形;然后只需考虑从剩下4个选项中选2个,与DE 的排列不符合的情况数(设有K种情形),所以答对3道题的有种情形.

根据这个思路,可以定义一种运算:设定m个不同的元素中的n个给定元素有一种人为规定的排列方式,从这m个元素中任选n个进行排列(即m选n,m≥n),记其中恰有p个元素处在规定位置的方法数为S(m,n,p).

例如,在“七选五”的题型中,假设正确的答案为ABCDE的前提下,则ABCEF 满足m＝7,n＝5,p＝3;BCGFA 满足m＝7,n＝5,p＝0.显然,S(2,2,1)＝0,S(2,2,0)＝S(2,2,2)＝1,……

在“七选五”的题型中,根据前述的思路与定义运算,若学生答对3道题,则有

此时,很容易得到三条运算规则:

3.2 问题的解答过程

在“七选五”的题型中,设离散型随机变量X表示蒙对的题数,则X∈{0,1,2,3,4,5}.从7个选项中选出5个按一定顺序填入5个空位,所有可能的情况的种数为

当X＝5时,即全都做对的情况为

当X＝4时,即做对4题的情况为

且可得S(3,1,0)＝2.

当X＝3时,即做对3题的情况

且S(4,2,0)＝7.

当X＝2时,即做对2题的情况

当X＝1时,即做对1题的情况

当X＝0时,即做对0题(全错)的情况

表1

为了便于观察,可以对概率进行近似计算,以百分数表示X的近似概率分布列,如表2所示.

表2

3.3 问题的结论

根据X的概率分布列,可以得出以下结论:

(1)全蒙错的概率约为48.17%,也就是说,有接近一半的概率一分也得不到;

(2)概率随着蒙对个数的增大迅速减小,全蒙对的概率仅有0.04%;

(3)计算出X的数学期望(即均值)为

(4)由于“七选五”的题型中,每题2.5分,设离散型随机变量G表示这道“七选五”的得分,则E(G)＝,平均得分仅约为1.79分,也就是说平均蒙对的题的个数不到1个.

4 第二种蒙题方式的分析

既然第一种“蒙”题方式的期望得分如此低,那么能不能用另一种蒙题的方式,即从7个选项中随机选出1个,然后五个空都填这个选项(比如五个空都填A),使得得分更高?

显然,改变蒙题的方式后,随机变量X服从两点分布,其分布列如表3所示.

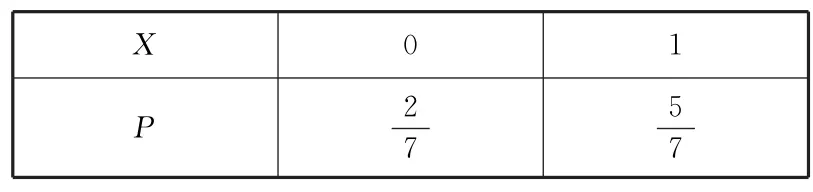
表3

此时X的数学期望(即均值)为

所以改变蒙题的方式后,X的数学期望、平均得分与第一种蒙题的方式没有区别,得分相同.

通过对两种蒙题方式的分析,可以知道:

(1)高考英语“七选五”题型的设置是科学的,能有效防止通过蒙题的方式得到高分;

(2)英语的“七选五”题采用蒙题的方式答题,其期望得分是非常低的,所以蒙题是非常不明智的举措,如果你不想落入这种窘况,那就只有好好学习了.

5 进一步思考

根据前述的运算性质,可以得到

因此,在“m选n”的问题中,答对题数的数学期望是

(完)