成对数据的统计分析常见题型研究

侯有岐(正高级教师 特级教师)

(陕西省汉中市四〇五学校)

成对数据的统计分析是高考概率与统计考查的重点内容之一.这部分知识要求学生从过去的单变量观察阶段转变到多变量的数据理性分析推断阶段,往往聚焦数学核心素养,以解决生产生活中的实际问题为背景,考查学生的必备品格与关键能力,深受命题者的青睐.本文对成对数据的统计分析考查的常见题型及解题策略进行总结.

1 成对数据的相关性

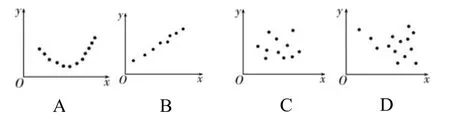
例1(1)(多选题)下列各图中,两个变量x,y具有相关关系的是( ).

(2)已知变量x和y满足关系式y＝－0.2x＋3,变量y与z正相关,则下列结论中正确的是( ).

A.x与y正相 关,x与z负相关

B.x与y正相关,x与z正相关

C.x与y负相关,x与z负相关

D.x与y负相关,x与z正相关

(3)两个变量y与x的回归模型中,分别选择了4个不同模型,它们的决定系数R2如下,其中拟合效果最好的模型是( ).

A.模型1的决定系数R2为0.98

B.模型2的决定系数R2为0.80

C.模型3的决定系数R2为0.50

D.模型4的决定系数R2为0.25

(2)因为y＝－0.2x＋3的斜率小于0,故x与y负相关.因为y与z正相关,可设z＝by＋a,b＞0,则z＝by＋a＝－0.2bx＋3b＋a,所以x与z负相关,故选C.

(3)在两个变量y与x的回归模型中,它们的决定系数R2越接近1,模型拟合效果越好,在四个选项中A 的决定系数最大,所以拟合效果最好的是模型1.故选A.

1)散点图法:如果所有的样本点都落在某一函数的图像附近,那么变量之间有相关关系;如果所有的样本点都落在某一直线附近,那么变量之间有线性相关关系.

2)相关系数法:利用相关系数判定,|r|越趋近于1,相关性越强.

3)决定系数法:利用决定系数判定,R2越接近1,模型的拟合效果越好,相关性越强.

2 回归方程的求法及回归分析

例2某种机械设备随着使用年限的增加,它的使用功能逐渐减退,使用价值逐年减少,通常把它使用价值逐年减少的“量”换算成费用,称之为“失效费”.该种机械设备的使用年限x(单位:年)与失效费y(单位:万元)的统计数据如表1所示.

表1

由表1数据可知,可用线性回归模型拟合y与x的关系,请用相关系数加以说明(精确到0.01).

参考公式:相关系数

因为y与x的相关系数近似为0.99,所以y与x的线性相关程度相当大,因此可用线性回归模型拟合y与x的关系.

2)确定R2:

例3某高中生参加社会实践活动,对某公司1月份至6月份某种配件的销售量及销售单价进行了调查,销售单价x(单位:元)和销售量y(单位:千件)之间的一组数据如表2所示.

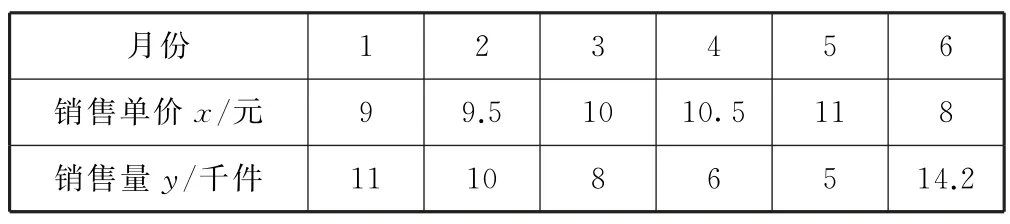
表2

(1)根据1月份至5月份的数据,求y关于x的回归直线方程;

(2)若由回归直线方程得到的预报值与实际数据的误差不超过0.5,则认为此回归直线方程是理想的,试问(1)中的回归直线方程是否理想?

(2)由(1)知,当x＝8 时,14.4,此时有14.4－14.2＝0.2＜0.5,故可认为(1)中所得到的回归直线方程是理想的.

例4某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响.对近8年的年宣传费xi和年销售量yi(i＝1,2,…,8)数据作了初步处理,得到下面的散点图(如图1)及一些统计量的值.

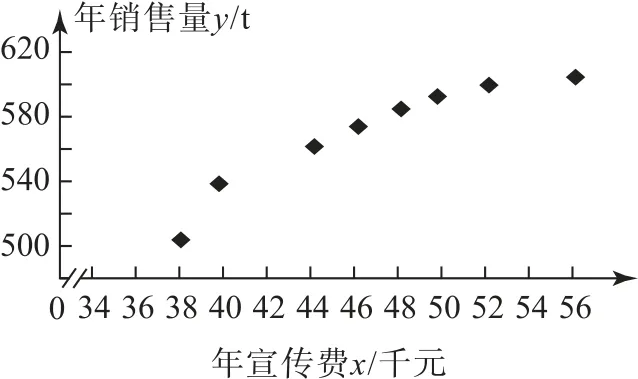
图1

参考数据:

(2)根据(1)的判断结果及参考数据,建立y关于x的回归方程;

(3)已知这种产品的年利润z与x,y的关系式为z＝0.2y－x.根据(2)的结果回答下列问题:

(ⅰ)年宣传费x＝49时,年销售量及年利润的预测值是多少?

(ⅱ)年宣传费x为何值时,年利润的预测值最大?

附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其经验回归直线的斜率和截距的最小二乘估计分别为

(1)由散点图可以判断,适宜作为年销售量y关于年宣传费x的回归方程类型.

所以y关于w的经验回归方程为因此y关于x的回归方程为

(3)(ⅰ)由(2)知,当x＝49时,年销售量y的预测值,年利润z的预测值

2)利用经验回归方程进行预测,把经验回归方程看作一次函数,求函数值.

3)经验回归方程的拟合效果可以利用相关系数判断,当|r|越趋近于1时,两变量的线性相关性越强.

3 独立性检验

例5(2022年全国甲卷文17)甲、乙两城之间的长途客车均由A和B两家公司运营.为了解这两家公司长途客车的运行情况,随机调查了甲、乙两城之间的500个班次,得到列联表如表3所示.

表3

(1)根据表3,分别估计这两家公司甲、乙两城之间的长途客车准点的概率;

(2)能否有90%的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关?

表4

(2)列联表如表5所示.根据临界值表可知,有90%的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关.

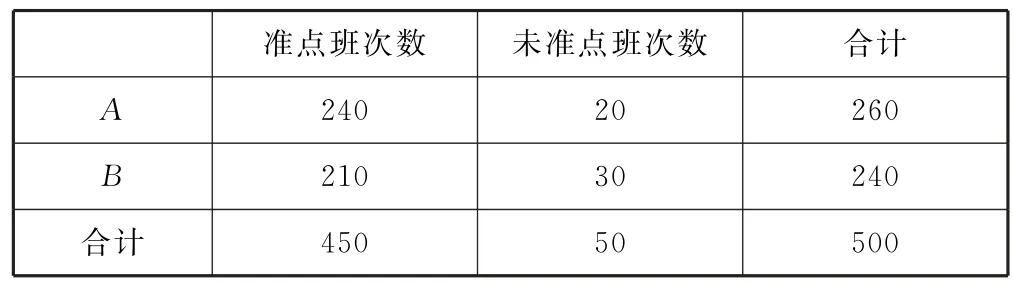
表5

1)2个明确:明确两类主体;明确研究的两个问题.

2)2 个关键:准确画出2×2 列联表;准确求解K2.

纵观近几年高考的概率与统计试题,成对数据的统计分析占有相当高的比重,而且命题形式也逐步趋于平稳,注重落实«中国高考评价体系»中四层四翼的考核要求.试题命制背景多与生产生活实际紧密联系,文字量大,信息多,对学生的阅读理解能力、信息获取能力和批判性思维能力有较高的要求.因此,笔者希望学生在复习中注重提高用数学概念、原理解读具体问题和提炼有用信息的能力,强化运算求解能力和统计推断思维.

(完)