基于参数化建模的桥梁模型截面优化程序的设计及应用

甘聪颖GAN Cong-ying；张辰啸ZHANG Chen-xiao；贾冬云JIA Dong-yun；王思源WANG Si-yuan；陶清林TAO Qing-lin

（安徽工业大学建筑工程学院，马鞍山 243002）

0 引言

近些年国内外学者在结构参数化设计、结构或构件优化等领域取得了丰富的研究成果。关于参数化设计方面，有对SolidWorks 进行二次开发的尺寸驱动法和程序驱动法[1]；有空间网格结构的可视化节点式参数化建模[2]。关于优化设计方面，有基于复形法与运用MATLAB 编程相结合的钢框架结构的优化[3]；有采用Midas 对结构设计竞赛模型进行轻量化设计[4]。上述研究中，参数化建模研究与结构、构件优化研究是相互独立的，本文基于APDL语言以参数化建模与自编“智选截面”程序相结合进行桁架结构设计与截面优化，使得桁架结构设计轻质、安全和便捷，并成功应用于结构设计竞赛的变参数桥梁模型设计中。

1 参数化建模与“智选截面”程序流程

1.1 参数化建模程序流程

首先选取合适的单元类型，定义材料的弹性模量、密度以及泊松比，对截面形式、截面尺寸以及截面惯性矩进行汇总，然后根据结构的最小节间长度作为模数，以节间数n 和腹杆长度系数m 为参数变量，通过调整参数创建节点坐标。连接相邻节点形成杆件，继而形成整体结构结构。最后在支座处施加约束，并根据荷载工况设置荷载分析步和加载节点。

1.2“智选截面”程序流程

应用参数化设计程序创建初始模型后，赋予各杆件最小截面（即表1 中截面号1）属性，静力求解后提取各杆件轴力，保留每根杆件在不同工况下的拉力T、压力P 极值，分别采用式（1）和式（2）进行强度和稳定性验算：

式中：T 为实际拉力值；Td为拉力设计值；A 为杆件截面积；f 为杆件抗拉强度；P 为实际压力值；Pcr为压力设计值；E 为刚度；I 为惯性矩；l为杆长；μ 为杆件计算长度系数。

经过式（1）和式（2）验算，满足要求的杆件保留其截面，否则升级其截面号，从而生成新截面号文件，进行下一轮求解、轴力提取、极值判断，直至所有杆件满足要求，保留截面号文件，即得到优化截面。

“智选截面”程序中对交叉腹杆采取了柔性设计，即交叉杆件工作时一杆受压另外一杆受拉，假定受压杆件屈服退出工作后，由拉杆平衡外力。因此这些交叉杆件在截面选择时被标注为特殊杆件，仅对拉杆进行强度验算，以求达到质量轻的目标。

模型结构参数化建模与“智选截面”程序的流程见图1。区域①为参数化建模流程，区域②为“智选截面”程序流程，二者通过循环读取与生成截面号文件建立联系，达到截面设计与优化的目的。

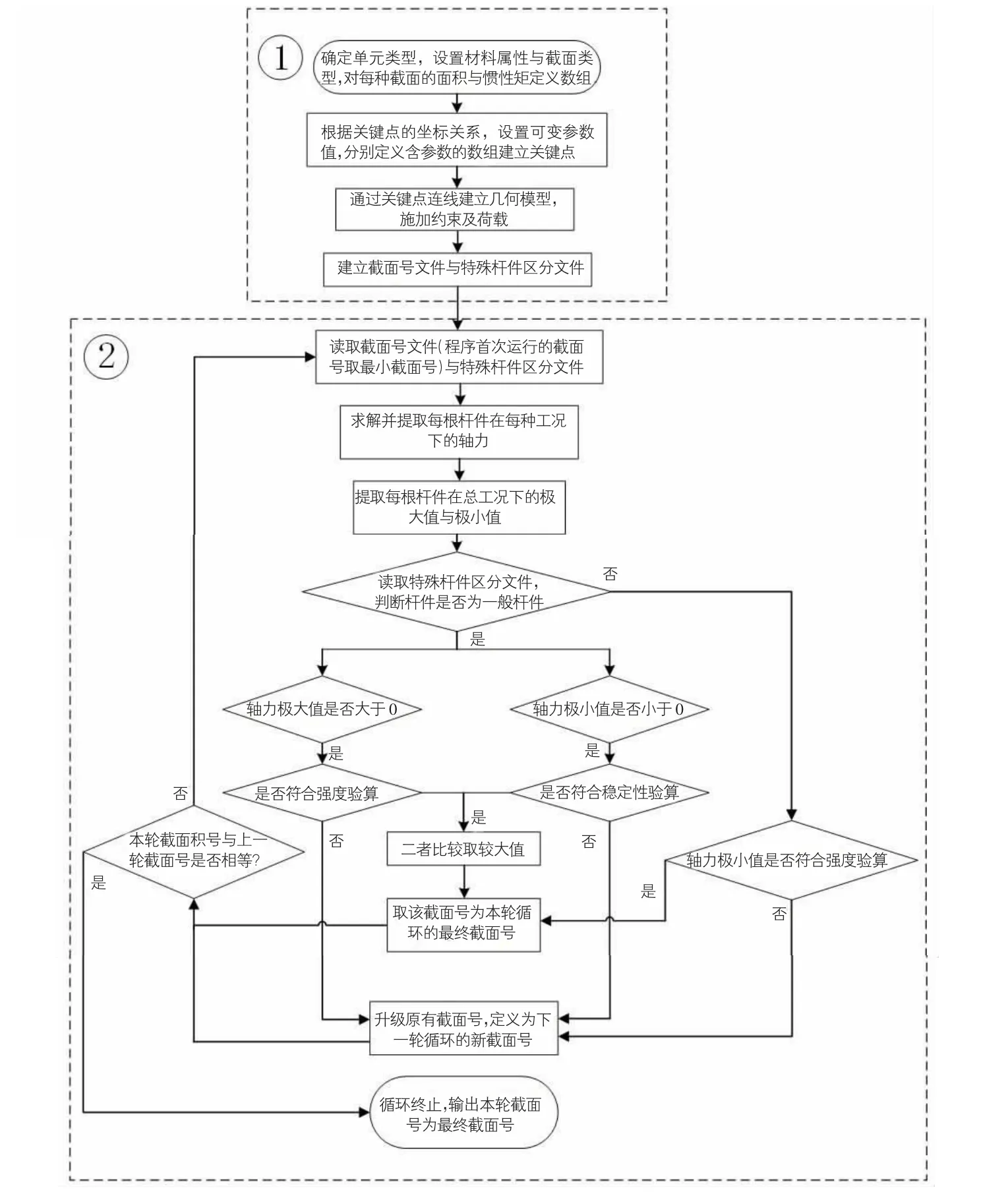
图1 程序流程图

2 赛题背景及特点

第十四届全国大学生结构设计竞赛赛题所设计的竹结构模型是承受竖向非对称静力荷载（砝码）和移动荷载（滚球）的桥梁结构，并且现场抽签随机选取桥梁模型的边界条件（支座位置）与荷载工况（悬挂砝码数量），以创新设计理念、质量轻、承载重并通过测试作为评价标准[5]。

根据赛题所提供的加载装置平面图（见图2）可知，②轴支座固定，③轴支座可在一定范围内移动，为模型结构形式提供自由发挥的空间。加载分为三级：一级加载是在八个加载点悬挂各不相同的待定荷载；二级加载可自由选择加载点，并分两次移动荷载，直到三点荷载集中于一点，形成不对称荷载；三级加载为小球移动荷载（见图2）[5]。因此，本桥梁模型设计是随机工况众多的变参数结构设计，必须通过力学分析与试验相结合确定模型参数。由于从抽签获得加载模式到赛场模型测试的时间有限，利用参数化建模和“智选截面”程序相结合的方式来完成模型优化设计为取得优异成绩提供了关键条件。

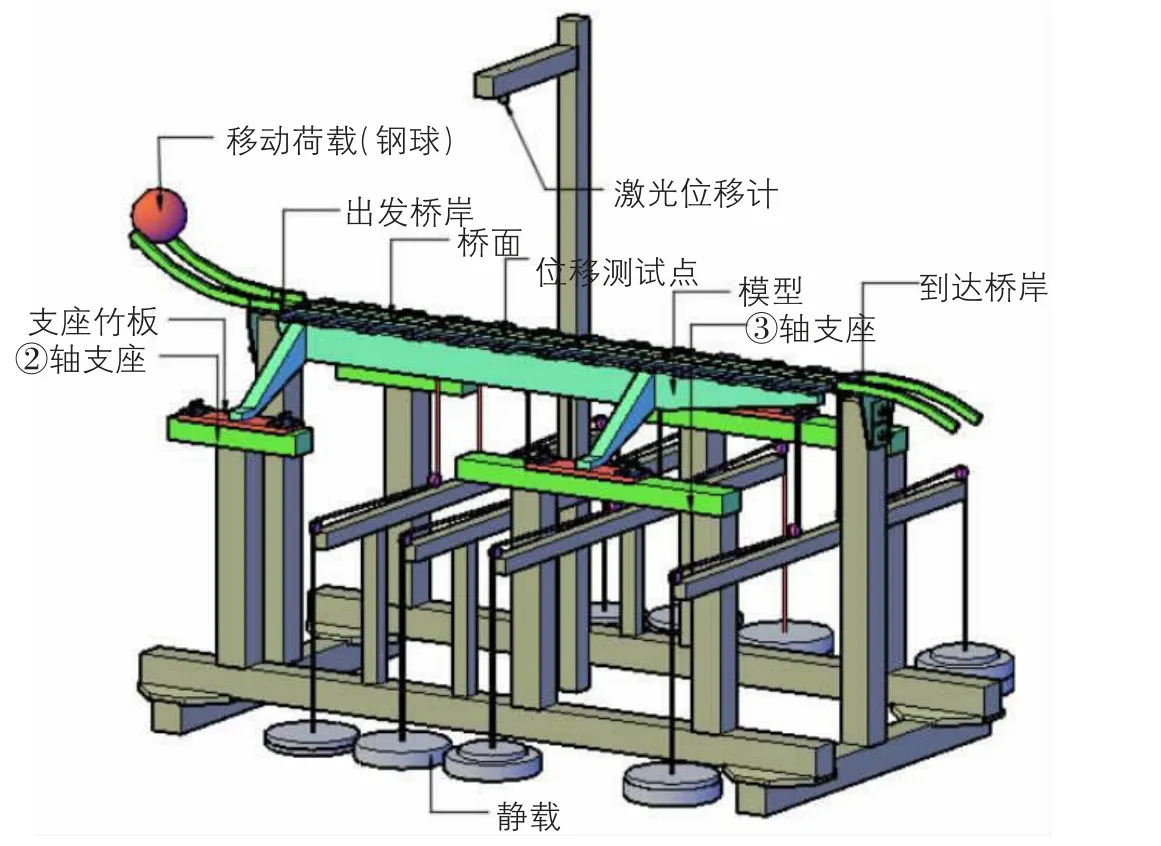
图2 加载装置图[5]

3 模型结构参数化建模与“智选截面”程序应用

3.1 模型结构参数化建模

根据比赛抽取的加载方案和支座条件，初步确定模型为桁架与斜拉索组合结构，如图3 所示。有限元模型单元类型为BEAM188 单元，首先定义材料属性：弹性模量E为5GPa，密度ρ 为1.49g/cm3，泊松比为0.3，顺纹抗拉强度f 为50MPa，抗压强度fc为30MPa。结构左端由两根斜柱（3号）支承上弦桁架，索塔（2 号）处两根斜柱（3 号）底部与索塔底部设置拉杆（7 号），分担斜柱承受的水平推力。桁架腹杆（6 号）均采用交叉杆件，有利于不对称加载和移动荷载作用下结构的稳定，并提高整体结构的抗扭性能。根据加载架的尺寸限制条件，可以确定上弦桁架总长1200mm，宽150mm，上部索塔高270mm，下部索塔高250mm，以及支座坐标。

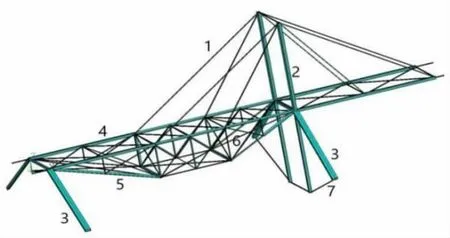
图3 模型图

根据所提供的竹材制作出适用于模型的杆件截面，截面按面积和惯性矩由小到大编号，截面信息见表1。将表中截面信息写入截面号的txt 文件，以便“智选截面”程序提取。

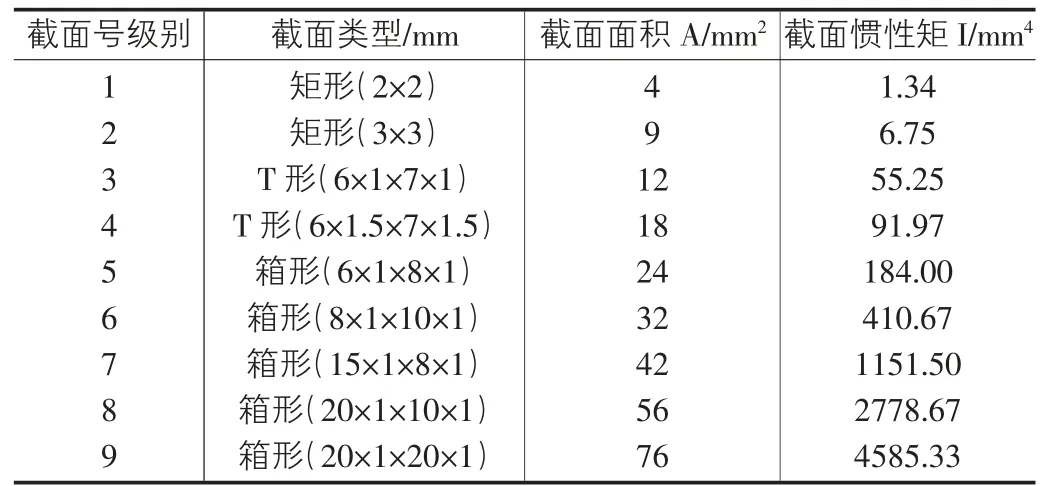
表1 各截面号级别与对应类型和截面属性

3.2 加载模拟

根据抽签情况确定了8 个加载点位置（见图4）和三级加载模式（见表2）。第一级加载为分别在8 个加载点悬挂工况I 荷载；第二级加载分两个工况：工况II 将加载点D2 上所有砝码转移至B2 加载点，工况III 将B2 加载点上的所有砝码转移至B1 加载点；第三级加载为50N 铅球移动荷载，属于缓慢加荷，可视为静载[6]，故将其换算成25N集中力按照四个工况（Ⅳ～Ⅶ）从左到右依次施加在上弦两侧的8 个加载点上。

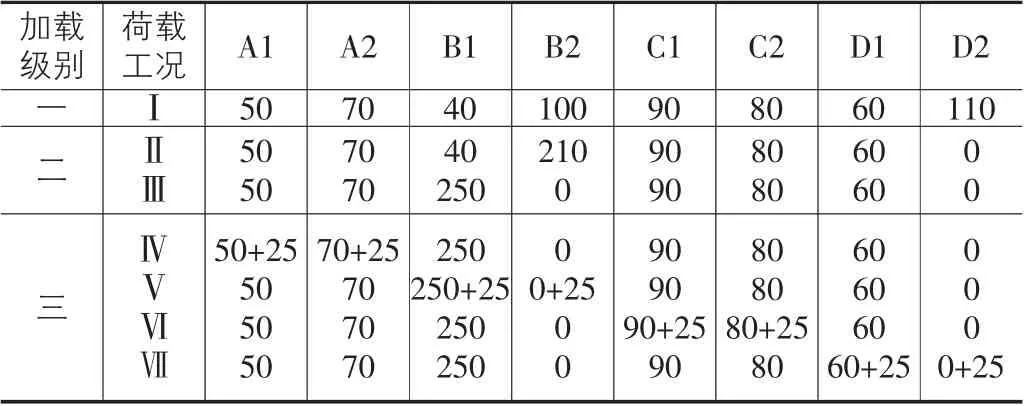
表2 不同荷载工况下各加载点的荷载 （N）

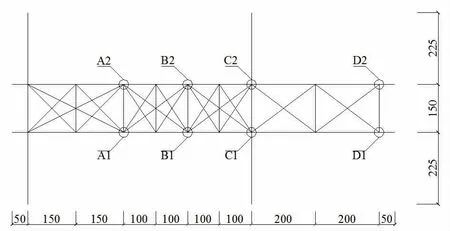
图4 模型加载点位置

3.3 杆件截面优化结果

运用参数化和“智选截面”程序在上述加载条件下对桥梁模型结构进行分析和截面优化。设置所有杆件的初始截面号均为1，经过三次循环迭代确定了每根杆件所对应的最终截面号。图5 为三次循环迭代所得模型结构的轴力和应力云图。

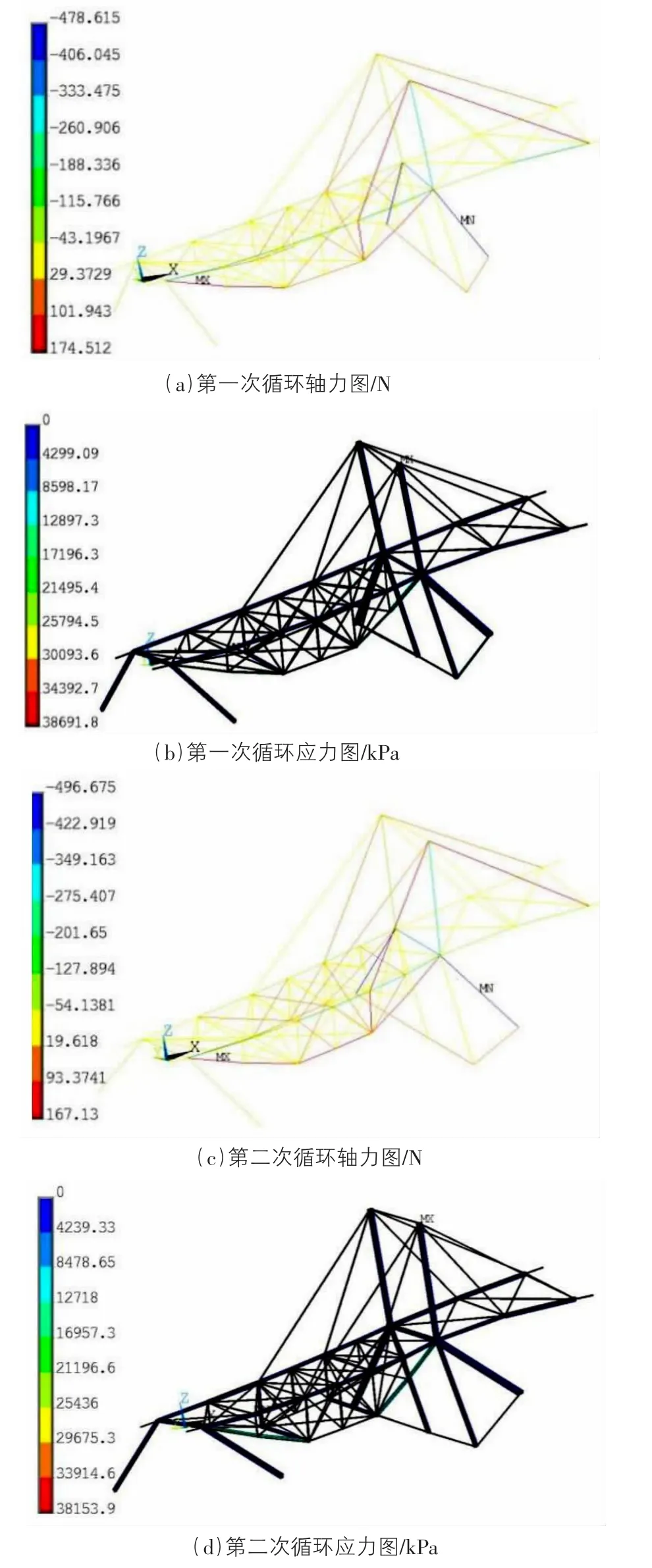
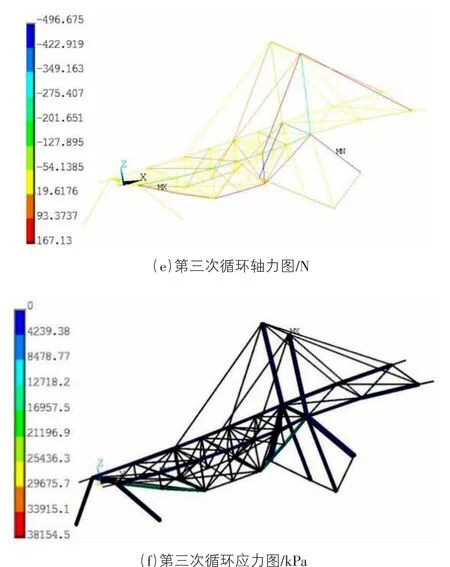
图5 三次循环迭代的桥梁模型轴力和应力图

三次循环迭代中应力变化较大杆件的单元编号见图6，对应的截面号和应力值见表3。由表3 可见：①下弦杆（19 号、21 号）轴力增加明显故截面号也随之增加，应力减小；②拉索（94 号、96 号），轴力变化不大，故截面号保持不变；③斜柱（107 号）位于支座，轴力较大，故经一次循环后截面号变化明显，后两次轴力变化不大，故截面号保持不变；④塔柱支座与斜柱之间的拉杆（112 号）三次循环的过程中由于内力重分布，杆件截面呈现增加再减小的现象；⑤交叉腹杆（77 号、85 号）工作时一杆受拉另一杆受压，且所受轴力较小，故截面号保持为最初始截面。

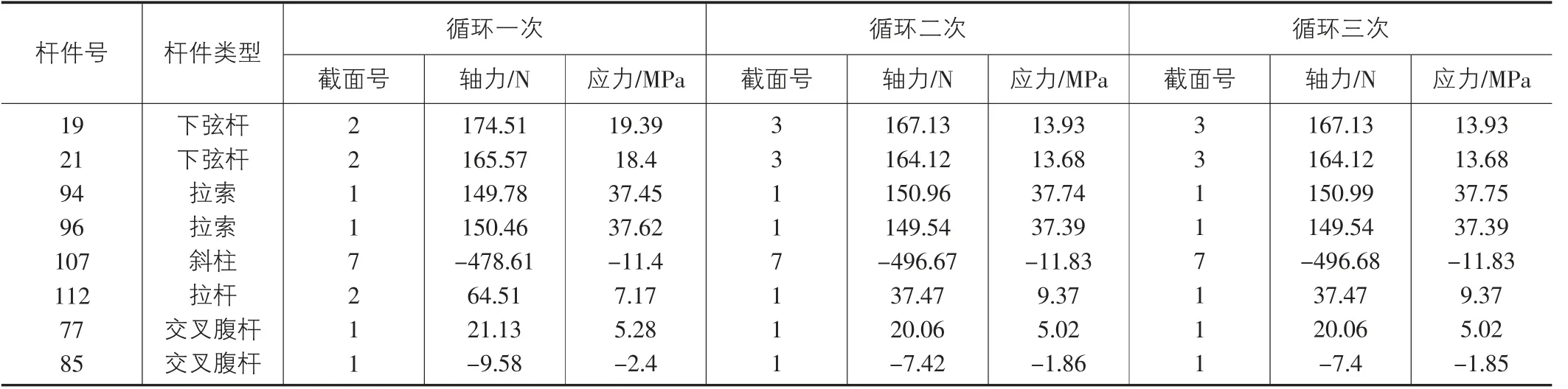
表3 三次循环后的关键杆件的截面号、轴力与应力

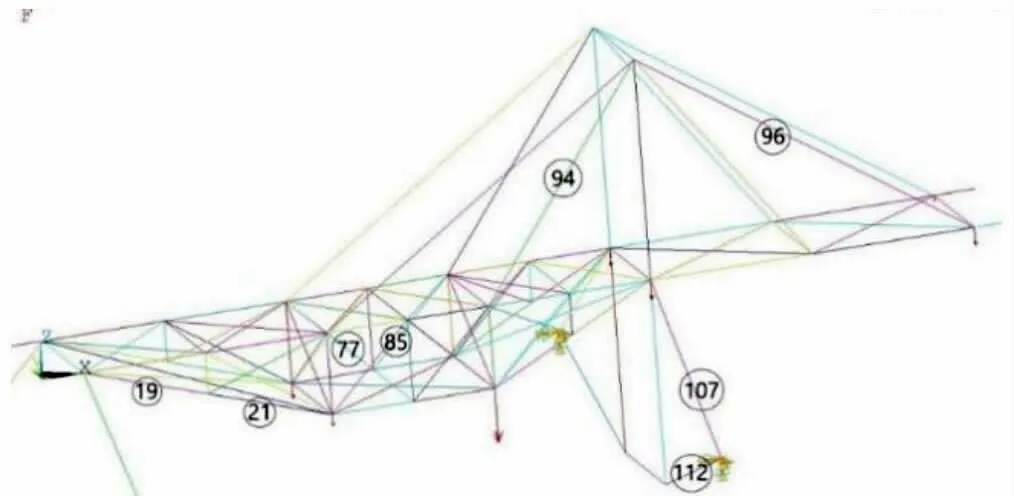
图6 模型关键杆件单元编号

3.4 现场测试结果

参赛队员根据程序所得模型的尺寸和杆件截面进行桥梁模型制作，按照抽签的加载工况进行加载操作，模型在每级加载时均满足承载力要求，并顺利通过移动荷载测试。图7 为小球滚过桥面板时模型的状态。

图7 桥梁模型现场加载试验

4 结论

①初始设置桥梁模型各杆件的截面号后，应用参数化和“智选截面”程序优化的杆件截面，经过三次循环所得各杆件的应力变化不同，表明截面优化效果明显。②实际桥梁模型的杆件节点近似半刚性连接，程序中应用欧拉屈曲失效准则验算压杆失稳，低估了结构的承载能力。实际模型制作产生的杆件和结构的初始缺陷会降低结构的承载能力。③参数化建模与“智选截面”程序的成功结合，不仅可运用于变参数桥梁模型设计，也可应用于实际工程设计。