基于GVF模型的地物边界边缘优化方法

彭刚跃 郭珍珍 何齐学

(1. 河南省水利勘测设计研究有限公司, 河南 郑州, 450000;2. 黄河水文勘察测绘局, 河南 郑州, 450000;3. 河南省第二建设集团有限公司, 河南 新乡, 453000)

0 引言

采用计算机对遥感影像进行地物的自动化提取时,得到的边界难以与实际边界相匹配,在提取之后需要采用一定的方法优化提取结果[1-2]。在现阶段的边缘优化研究中,活动轮廓(active contour model:Snake)模型应用较为普遍,研究者在采用Snake模型时做出了多种改进,比较经典的包括：气球力Snake(balloon-Snake)模型,距离Snake(distance-Snake)模型,梯度矢量流(gradient vector flow,GVF)模型,而GVF模型由于其稳定和准确的特点,受到大量学者的关注[3-7],现已广泛应用于医学、人工智能等领域。

本文对GVF模型的原理和实验数据进行分析,在此基础上提出一种改进的GVF模型,应用于遥感影像中的地物边界提取与优化,通过对该模型的分析和实例验证,证明本方法能够有效地避免边界偏向影像灰度值的突变点,更加贴近真实的地物边界。

1 GVF模型

1.1 Snake模型

Snake模型是由Kass等于1987年提出,其思想是通过把图像上的底层信息和地物的高层知识进行结合,综合考虑图像中地物轮廓的几何特征与图像整体的内部特征,计算能量函数并进行迭代,逐渐趋近其真实边界,最终确定地物的轮廓,其计算过程就是图像力平衡的过程[8]。

假设在图像中,x、y表示初始提取的轮廓线的坐标,轮廓线的数学表示为

(1)

将轮廓线的能量函数定义为

(2)

式中,Eint是指轮廓线的内部能量,与轮廓线的平滑和连续性有关;Eext是指轮廓线的外部能量,与图像整体有关,其定义分别为

(3)

式中,α与曲线的连续性有关;β与曲线的刚性有关。当α等于0时,曲线可能出现断点;当β等于0时,曲线出现转折点。

(4)

1.2 GVF模型

梯度矢量流模型(GVF模型)是在Snake模型的基础上,将梯度向量流作为图像力,代替原来的外力,其中,梯度向量流的数学表示为[9-10]

(5)

式中,μ、ν代表图像中(x,y)点位置沿着两个方向的梯度,V由极小化式(6)的能量泛函来计算

(6)

(7)

(8)

基于上述理论,本文采用GVF-Snake模型对提取得到的边缘进行优化处理,参数选择α=0.05,β=0.1,γ=1,κ=0.6,以道路与海岸线为例,分析该模型的优化结果如图1所示。

(a)原始道路边界

从图1可以看出,海岸线和道路优化后的边界与真实边界存在部分区域重合度不高的情况,这是由于采用GVF模型的计算规则主要基于梯度矢量流,易受到周围图像突变的影响,使得曲线在移动过程中逐渐偏向图像突变的区域。

2 改进的GVF模型

由于上述问题存在,本文提出将兴趣地物的灰度值加入该模型的外部能量中,对GVF模型的算法进行改进。若兴趣地物的灰度均值为x1,灰度阈值范围为d1,根据x1和d1将图像分为属于兴趣区域的点集A和不属于兴趣区域的点集B。对A中的每个点计算其距离B中点最近的距离作为该点的势能D,对B中的每个点计算其与A中点最近的距离作为该点的势能[13-15]D。Snake模型中的外部能量函数可以表示为

(9)

式中,EGVF表示由图像梯度矢量流构成的外部能量;ED是指距离势能;λ为权重参数,取值范围为(0-1),λ=0时,外部能量由距离势能构成,λ=1时,外部能量由梯度矢量流构成。

通过数值化实现后得到外部能量函数的偏导数为

(10)

式中,u(xi,yi)、v(xi,yi)分别表示GVF离散化之后得到的结果;∂D/∂x、∂D/∂y分别表示距离势能沿着x、y方向的偏导数。采用该方法对海岸线和道路的初始轮廓进行优化,其流程如图2所示。

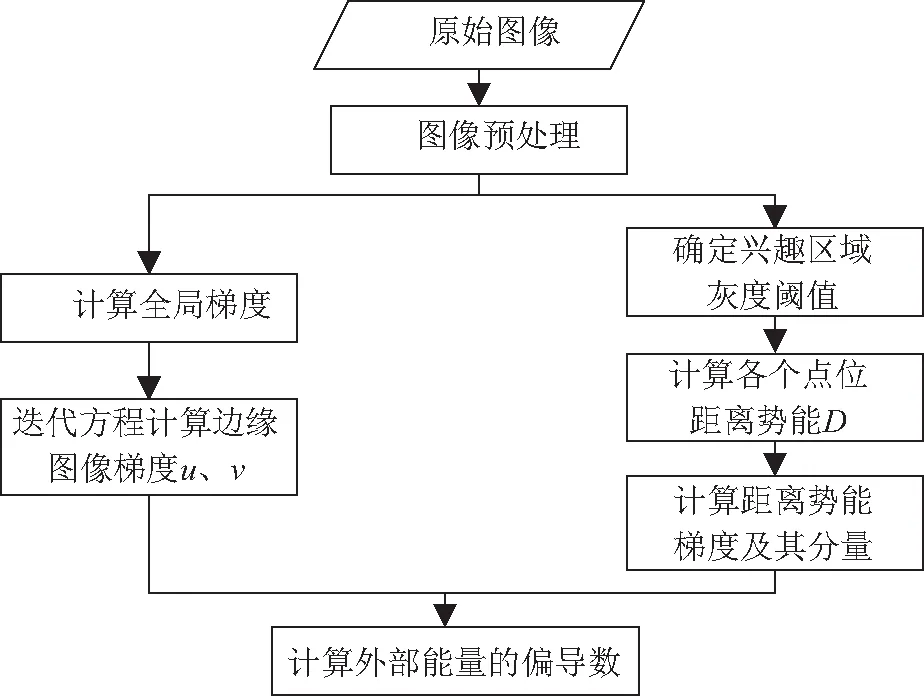
图2 改进的GVF模型计算流程图

3 实例分析

对GVF模型进行上述改进后,与原来的计算方法相比增加了图像外部能量的来源构成,减弱了梯度矢量流对边缘优化过程的影响,用该方法对道路和海岸线的初始轮廓进行优化,与GVF模型优化的结果进行对比,得到结果如图3所示。

(a)GVF优化的道路

从图3可以看出,图3(a)与图3(c)中有少量点位向干扰区域靠近,使得曲线偏离道路或海岸线边界,这是由于图像中存在灰度值突变的点或区域,使得边界曲线在用GVF模型计算时会偏向该类区域,影响优化结果。图3(b)与图3(d)中较好地消除了该类影响,避免陷入干扰区域,与实际边界贴合程度较高,点位分布效果较好。

4 结束语

通过GVF模型可以将计算机提取的初始轮廓进行边缘优化,但由于模型本身的局限,其较易受到周围图像突变区域的影响,使得优化结果偏离真实边界。本文首先对Snake模型和GVF模型的原理进行分析,在GVF模型的基础上将距离势能加入计算,与梯度矢量流共同构成模型的外部能量。通过实验分析可以看出,该方法可以有效改善周围图像的突变对优化结果造成的影响,优化结果与实际边界匹配程度较高,在GVF模型的基础上增加了参数输入,增加了模型复杂度,减少参数、提高自动化程度将是需要进一步研究的方向。