基于InSAR复数影像配准方法研究综述
唐固城 谢丽芳 刘 烜
(1. 浙江省测绘科学技术研究院, 浙江 杭州 310023;2. 浙江省国土勘测规划有限公司, 浙江 杭州 310030)
0 引言
合成孔径雷达干涉测量[1](synthetic aperture radar interferometry,InSAR)是一种主动式的微波遥感系统,因拥有全天候、全天时,并能大面积获取数据的特性,近年来已在地表变形监测及数字高程模型(digital elevation model,DEM)等领域中得到充分应用[2]。目前合成孔径雷达(synthetic aperture radar,SAR)干涉处理技术已趋于成熟,主要流程主要包括影像配准、干涉图生成、去平地效应、相位解缠以及地理编码等步骤。而SAR复数影像配准是合成孔径雷达干涉技术的首要步骤之一,它的配准精度是直接影响干涉图的生成质量以及最终成果精度与可靠性。研究表明,配准误差精度一般要求达到1/8以下像素才对后期干涉图的质量无明显的影响[3]。
配准是解决影像之间内容不一致的问题,由于获取两张影像时的卫星观测状态不一致导致相同影像坐标对应的地物目标点有差异。雷达影像不同于光学影像,它受斑点噪声的影响较光学影像严重而导致实现高精度的配准较难;因InSAR影像数据为单视复数,数据中除了幅度信息外,还包含有相位信息,重复轨道模式下获取的影像相对位置随着轨道位置的变化而变化,也导致配准的工作难度加大。为了克服噪声对配准结果的影响,实现高精度的配准结果,近年来许多国内外学者针对SAR复数影像配准这一领域相继提出了相关方法,如黄其欢[4]等提出了方差因子检验和Baarda数据探测法剔除粗差控制点方法,Sun[5]提出基于R-RANSAC算法的控制点选取配准法,Fang[6]基于Voronoi图的InSAR影像控制点配准算法,陈华[7]提出了基于尺度不变特征变换(scale-invariant feature transform,SIFT)和随机抽样一致性(random sample consensus,RANSAC)配准法,Chen[8]提出的基于SAR图像几何特征点信息的InSAR图像配准方法,Dellinger[9]提出一种基于类尺度不变特征变换的SAR复图像配准算法,李彦锋[10]提出了基于端到端网络的SAR图像配准方法,该方法通过分析单阶段预训练网络的优势进一步改进单阶段深度学习方法;张娇娇[11]提出了基于改进SIFT和深度学习的SAR图像配准方法等。由此可见;对于配准方法的相关研究可归结为主要围绕控制点选取优化、影像几何关系特征及深度学习三个方面。本文以SAR影像振幅、相位、灰度值为核心信息,从控制点选取优化、几何影像特征及基于深度学习三方面总结配准方法的优缺点,并对该领域未来研究方向进行展望。
1 影像配准基本原理
获取的影像除了可以从同一传感器上在不同的时间或者从不同的角度获取,还来自不同的传感器系统。由于获取的雷达影像为复影像,可用公式表示为
(1)
雷达影像的配准是将同一目标地区的两幅或多幅影像在空间位置上实现最佳套合。其原理是利用两个信号相关函数,通过某种相似度准则来评价两幅影像之间的相似度。其一般步骤如图1所示。
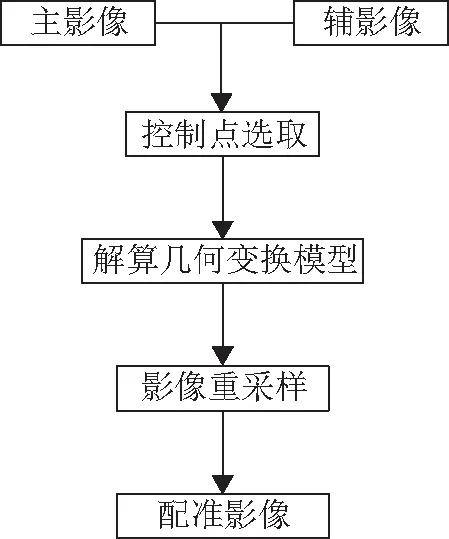
图1 影像配准步骤
控制点选取核心在两幅及以上影像之间准确选取具有相同性质的同名点,以它作为配准的基础,不同的传感器及不同时段获取影像的几何、物理等特性也不尽相同,因而匹配的方法也有差异[12]。确定了影像之间的同名点后,需要对影响对之间的位置进行几何变换,一般采用的模型为多项式,已知一组同名点,辅影像坐标为(x,y),主影像相对应坐标为(x′,y′),其多项式可表示为
(2)
式中,n为多项式阶数;aij、bij为待定系数,一般采用最小二乘法求解各项系数。
当影像完成相对纠正后,需要对辅影像进行灰度重采样,得到经配准后的新影像,一般采用双线性内插法或三次样条内插法。
综合而言,配准影像对之间的关键点可归纳为两个方面,一是根据干涉成像的卫星观测几何特征推算斜距投影坐标下影像对之间的几何变换特性[13];另一是基于InSAR影像的特征信息,利用适宜的方法快速而准确地选取控制点。
2 控制点选取优化方法
控制点的选取对于影像的正确配准有着至关重要的作用,相干性系数法是经典的配准方法之一,它充分利用了影像中包含的相位及振幅信息在主影像中以待匹配的点为中心取一定大小窗口,在辅影像中一定范围内搜索,计算窗口内的相干系数值,最大即为最佳匹配点。由于相干性系数[14]难以准确获取,Gbariel[15]等提出了基于信噪比的最大干涉频谱法,该方法充分利用了影像的相位信息,当影像之间的干涉图质量达到最佳即为最佳的配准。而平均波动函数法[16]是以同名点领域内相位差变化的一致性作为判断准则。此外还有相关系数法[17],最小二乘匹配法[18],这些方法都在于准确寻找出合适的控制点,它们的特点如表1所示。

表1 传统配准法
2.1 基于传统方法改进
在单点匹配的传统方法中,部分匹配测度是在一个相对较小区域内计算的估计值,也未充分利用影像中所包含的强度信息,对于传统单点匹配方法存在的不足,不少学者提出了多级配准[19]方法。卢丽君[20]利用相关系数与最大干涉频谱相结合的多级配准算法,并针对较大范围影像数据处理引入了并行处理方案,利用三峡地区实验结果表明经过粗、精配准后,中误差由0.517 8降为0.058 1。该方法较传统的单点匹配在一定程度上提高了计算的效率及精度因素。汪鲁才[21]基于最大频谱法中引入相关匹配函数法,利用相关匹配实现粗配准,并对控制点值进行内插,再利用最大频谱图像配准实现亚像素精配准,通过喀什地区实验结果表明随着相关系数值越大,相关精配准与最大频谱精配准处理结果中像素点数也在减少。该方法较最大干涉频谱法有较高的计算效率。张宗营[22]利用相关系数法与重采样相结合的多级配准策略,并利用西藏那曲市实验结果表明,控制点对应关系数均值从粗配准的0.49提高到0.7,影像试验表明了多级配准方法在精度及可靠性方面的优势。Suo[23]提出一种基于最小二乘法(LS)的联合配准法,该方法利用具有小空间和时间基线的图像对求解估计影像偏移,采用Delaunay三角剖分方法进行连接,根据基于最小二乘法估计的图像位移对所有辅图像进行重采样。
传统配准方法对于InSAR观测时轨道不平行影像配准结果无法达到最优,Nicolas[24]在相干系数法的基础上结合Fourier-Mellin变换函数,一定程度上解决了存在夹角的InSAR影像之间的配准问题。为克服常规SAR影像配准中由于离散窗口移动搜索导致配准误差而致使相干性损失的问题,程海琴[25]提出利用卫星轨道状态矢量与SAR定位模型进行影像粗配准点,利用基于相干窗口进行像素级配准和基于相干曲面移动拟合的精配准方法,通过选取平原及山地区域进行试验,结果表明影像相干性均约有5%的提高,同名点的影像配准精度达到了(0.01~0.1)像素。鉴于大场景影像中不同区域偏移量及变化规律差异较大,传统最大相干系数配准方法再处理时需分块及插值处理,面临计算量大且配准精度低等问题,韦顺军[26]提出一种基于离散傅里叶变化模型的大场景InSAR高效高精度图像配准算法。利用基于最小均方差准则构建配准的DFT模型,采用四叉树自适应分块及矩阵相乘DFT快速重采样配准方法,实现大场景影像各子块区域的高效高精度亚像素配准。通过富士山区域实验表明与传统的FFT分块方法相比,该方法在残差点数、相干系数均值及相位梯度均值三个指标上较之分别减少8 274个、增加0.067 2、减少0.006 8。
2.2 基于粗差控制点剔除改进
针对SAR影像易受噪声干扰导致在寻找最佳同名点的过程中出现多个错误极值的情况,有少数匹配结果不在合理范围内,相关学者在控制点选取可靠性及效率方面提出了不同的方法。Petar[27]使用Harris算子进行配准点自动检测,提高了配准点数量并改善了其空间分布;王孝青[28]从矩阵相似度的角度分析干涉影像对之间的相关性,给出了一种加权相似度度量,并提出了检测和剔除噪声干扰原理和方法,提高了配准精度和可靠性。意大利学者Sansosti[29]提出的利用地面控制点方法计算两个方向上的时间参数,但对于较大的数据进行选择时较难实现高精度配准,刘广[30]对Sansosti提出的基于地面控制点计算时间参数的配准方法进行改进,在此基础上提出了一种主动获取方向与距离向的时间常数的配准法,但该方法需要精确的轨道数据和大量的控制点来实现。
针对低相干、低信噪比区域出现错误匹配,孙增辉[31]在基于信噪比的基础上针对控制点的正确选取方面,提出了利用总体方差检验和趋势面参数模型粗差诊断法实现控制点粗差检测及剔除,提高了影像之间的配准精度。实验表明,经过粗差剔除后,方位向最大残差0.603 4像素降到0.088 6,距离向最大残差0.258 0像素降到0.079 1像素。Zhang[32]提出了一种基于InSAR相干变化检测的有效地理配准方法。该方法通过计算地面控制点(ground control point,GCP)周围的张性子图像的互相关和周围子图像的强度互相关值,从而获得距离和方位偏移量值。除此之外,王邦松[33]采用Voronoi图方法对影像中特征点进行进一步优选,通过与传统的方法(如最大频谱法等)相比较,经粗差剔除后匹配点间成功率达100%。
3 基于影像几何关系特征方法
基于特征的影像配准方法,也是影像配准常用的方法之一。该方法从不同影像中提取具有代表性和相似的特征量,经常用到的影像边缘、轮廓及结构特征等。基于特征的影像匹配方法一定程度上压缩了影像的信息量,使得减少了计算量,并对影像的灰度具有较好的鲁棒性。
3.1 基于影像特征信息改进
边缘信息是影像常见的结构特征,也是SAR影像中重要的信息之一,单一的边缘检测方法实现SAR影像的配准精度不足以满足要求,因此学者提出了联合边缘信息与其他方法相结合。张泽昆[18]提出了一种基于边缘和纹理特征相结合的图像配准方法,它以边缘和纹理作为基本特征,通过纹理特征的提取对经边缘特征提取后的影像进行修正来提高配准精度。R.Scheiber[34]提出基于频谱差别的配准方法,该方法以SAR影像为模型,不需地面控制点,然后利用相位与配准偏移量的关系得到偏移值。刘宝泉[35]通过边缘检测和模板相关提取特征点,建立点的对应关系,然后利用两步法完成复图像的亚像元级配准,具有较高的配准精度,实验结果较基于区域特征方法,该算法均方根误差与之相比减少了0.005 7,表明基于点特征的全自动配准方法有较高的精度。
SIFT算法是一种基于特征点匹配算法,该方法在影像缩放、旋转等变换下能保持较好的配准效果,因而被应用于SAR影像配准。喻小东[36]等提出了基于SIFT算法的配准方法,该方法采用分块方式提高影像匹配效率,通过设定阈值减少配准误差点,并通过Enta火山地区实验分析可知,相较基于相干系数法,均方根误差(root mean square error,RMSE)由1.51降到0.32。Zhu[37]提出了一种新的合成孔径雷达图像配准方法,包括两个用于特征检测的算子SIFT和R-SIFT用于检测SAR图像中的角点和纹理点和用于特征匹配的树状网络匹配(ANM),该方法的优点是能同时保留SAR图像中的两种特征信息,该算法将特征约束与特征点之间的空间关系结合起来,具有更多的匹配对和更高的亚像素匹配精度。实验结果表明,相比KNN-TAR方法,该算法RMSE降低了0.632 8,BPP(残差距离大于1.0像素百分比)降低了0.527 1。SIFT算法因不需要额外的信息(如轨道参数),直接根据幅度获取较为精确的偏移多项式,但该方法中使用的特征向量依赖与主方向,如果影像中无明显的纹理信息,该方法配准精度难以保证。
除边缘信息外,SAR影像还有纹理、振幅等特征信息。焦明连[38]等提出了一种充分利用复数影像中幅度分量所包含的信息进行多种匹配的方法,该方法可确保匹配结果的精度达0.1个像素以上。InSAR技术所获取的影像除复数影像外,其辅助数据里包含卫星传感参数、遥感平台过程中位置矢量及相对应的时间参数、影像四角和中心地理坐标等信息,汤晓涛[39]提出了一种基于辅助数据的对SLC影像的基线进行估计并自动进行影像概略配准法,经过数据验证斜距方向上偏移量达到5像素,方位向上偏移量达10像素。
3.2 基于外部数据辅助方法
SAR卫星所获取的影像的轨道近似平行,利用DEM数据根据主影像参数模拟SAR影像,并利用移动窗口技术获取与辅影像的粗略偏差,确保影像之间的相干性不会受到配准的影响,当利用几何配准精度不足时,利用DEM数据信息能确保估计影像的偏移量值。
王超[40]提出了一种基于DEM的自适应配准算法,该方法解决了在复杂地形下因测度函数选取单一导致配准精度较低的问题,通过秦岭地区的实验结果表明,相较于互相关系数法及频谱极大值法,该算法所得干涉图的相干系数均值较之增加0.040 4、0.029 8。Massonner[41]提出基于卫星轨道和外部DEM的配准方法,该方法对影像上所有像素都有相同的配准精度,即使在相干性较低区域也有较好的配准精度,但必须要获得方位向和距离向上的有效时间常数。针对Sentinel-1A成像方式导致SAR影像方位向多普勒频率变化较大,黄其欢[42]提出了基于DEM和精密轨道的TOPS影像高精度配准法,并通过实验表明粗差剔除后拟合的标准差方位向为0.173像素,距离向为0.077像素。吴文豪[43]利用Sentinel-1卫星TOPS影像进行不同轨道和DEM条件下几何配准测试,并分析了外部DEM对影像配准精度的影响,通过实验表明目前常用的外度DEM(如SRTM)均能满足Sentinel-1影像配准的要求,其几何配准差异在0.001像素内可任意选择不同类型。另外,Mao[44]等提出了一种利用多源信息和联合数据融合的影像自适应共配准方法,并使用均方差来评估配准方法的准确性。
4 基于深度学习配准方法
随着计算机存储和计算能力的提高,深度学习[45]在影像处理方面也得到了快速发展,尤其是卷积神经网络。深度学习在特征点的可重复性与匹配精度等指标中表现出较好的性能被广泛应用于影像检测、识别及分割等领域。目前深度学习应用于影像配准可概括为以下几个方面[46]:利用卷积神经网络替代人工进行特征提取,利用深度卷积神经网络通过有监督学习的方式直接对变换参数进行回归影像配准,利用深度卷积神经网络对变换后的图像与目标图像的相似性进行优化,通过无监督学习的方式实现图像的配准。
朱庆涛[47]等提出了将邻域一致性与稀疏卷积神经网络应用于影像配准中,实现利用弱监督学习的端到端极化SAR影像一步配准方法。常钊[48]提出了基于稀疏自编码(sparse autoencoder,SAE)的半监督SAR影像配准方法,通过调整网络参数从而是影像之间的配准达到较好的配准效果,但该算法人工干预较多,存在效率较低的缺点。Kelany[49]提出了一种基于传统神经网络学习的图像超分辨率改进SAR图像配准算法,该方法是将Scale-Invariant Super-Resolution与影像匹配相结合,从而实现了影像的配准,并通过温哥华地区的影像配准结果表明该方法得到的均误差为0.000 6,样本方差为0.003 7,标准差为0.060 9。
5 结束语
影像配准作为InSAR技术处理流程的首要步骤,它的准确度影响后续处理步骤精度,传统的配准方法适应性较差,特别是对复杂的区域,如最大干涉频谱法能克服SAR影像中与频率域有关噪声,但对于叠掩、阴影较多区域效果较差。为此,国内外学者对提高影像的匹配精度做了较多的研究,这些研究方法可以概括为基于控制点优化选取、影像结合关系特征及深度学习配准三个方面。这些算法在质量较好SAR影像或影像受固有噪声影响较小的情况下均能使复数影像之间的配准精度达到子像素级要求,但目前都存在不同的缺点。
对于基于控制点优化算法方面,主要存在控制点剔除算法判定的测度函数与统计量合理设计,控制点剔除影响算法的稳健性等问题。基于影像关系特征算法充分利用影像的边缘、轮廓及结构特征等信息,但对于受噪声影响严重的影像无法充分利用影像的特征信息,另外,外部DEM的精度也直接影响到影像的配准精度。目前深度学习的最大难点之一主要在于卷积神经网络学习中训练样本数量和样本集及复杂配准模型下如何优化神经网络的结构等问题。

