短期风电功率预测的深度学习模型

辛 征，王 琦，刘兴然

(山东建筑大学信息与电气工程学院，山东 济南 250101)

0 引言

近年来，随着化石能源的短缺和环境问题的日益严重，清洁能源发电的规模迅速扩大。风力发电以其清洁、经济、可持续发展的优点，已成为最重要的可再生能源发电方式之一。截至2021年底，全球风能总装机容量超过837 GW，2021 年全球风能总装机容量为93.6 GW[1]。虽然风力发电技术越来越成熟，但由于风力发电[2]的间歇性、随机性和不确定性，影响了风力发电以及电网的稳定性、安全性和经济性。同时，风电发电功率的不确定性也会对电力市场的设计、风电系统的规划与部署、电网调度、输电能力升级等问题产生影响[3]。因此，准确有效的风电功率预测技术是不可缺少的，对于风电的安全、稳定、经济运行具有重要意义。

目前，国内外众多学者对风电预测方法进行了综合研究。根据预测原理的不同，风电功率预测方法可以归纳为三大类:物理模型、机器模型和统计模型[4,5]。其中，物理模型依赖数值天气预报(NWP)提供的天气和风速信息，需要建立大数据模型。该方法适用于大范围的长期预测，不适用于小范围和短期预测。机器模型基于研究数据的时空分析进行预测，主要包括卡尔曼滤波(KF)[6]、回归方法[7,8]、指数平滑方法[9]和时间序列分析方法[10]。虽然机器模型在简单的时间序列预测和短期预测中表现良好，但在非线性数据处理方面存在不足。一般来说，统计模型在短期风电预测中优于物理模型。

1 风电功率影响因素分析

1.1 风速与风力发电功率的关系

风能作为风力发电的源动力，在空间的分布上是呈分散的，在时间的分布上是呈不稳定与不连续的，所以风能资源的时而大时而小、时而有时而无的特点决定了风速具有不稳定性与间歇性。

风机输出的可用功率由于受风速、风向波动等各种因素的影响会进一步的减小。图1为风速与风力发电功率的关系，风机的功率和风速的大小是正相关的。当风速愈大时，风机的功率也愈大，并且风速出现极大地时刻和风机的功率出现极大的时刻基本保持相同。

图1 风速与风力发电功率的关系

1.2 空气密度与风力发电功率的关系

影响风电功率的气象信息还包括温度、湿度等，这些因素主要通过空气密度而导致风电功率发生变化。温度、湿度与风力发电功率的关系如图2、图3 所示。空气密度ρ是决定风电机组发电功率的重要因素，特别是在高海拔地区，空气密度对风能得影响较为明显。相同风速下，随着空气密度的增大，风电机组的发电功率也相应变大。

图2 气温与风力发电功率的关系

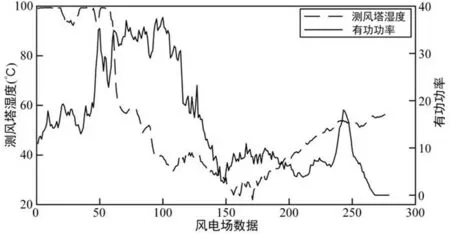
图3 湿度与风力发电功率的关系

1.3 斯皮尔曼相关性分析

风电功率转化过程中，风速、风向、气温、气压、湿度等气象因素都会对预测功率产生影响。单一的输入变量往往达不到预测精度的要求，而将所有特征作为预测模型的输入变量，将会影响模型的性能。因此，在建模时需要充分考虑影响风电功率的重要性特征。采用Spearman方法做相关性分析。计算两个n维向量x，y 的Spearman 相关系数方法如式⑴。其中x，y 表示进行相关性分析的两个变量。

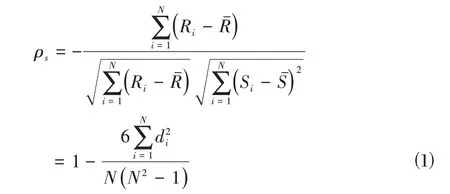
其中，Ri和Si分别是向量x，y进行排序后观测值i的秩次分别是向量x和y的平均秩次；N是i的总数量；di=Ri-Si表示两个变量中i的秩次之差。Spearman 相关系数中ρs是[-1,1]中的实数。当ρs＞0时，两个变量成正相关，反之，则负相关。|ρs|越大，变量x和y的相关程度越高。

采用相关性分析的方法，计算国内某风电场2019年的风电功率以及影响因素各变量数据间相关系数，分析情况如表1 所示。由表1 可知，发电功率和风速这个变量的相关性最大，相关系数为0.9405；而与风力发电功率相关程度最低的为气压，为0.0898，经过分析，将获取的实测数据中影响发电功率的主要变量为：风速、气温以及风向。

表1 风电功率与影响因子间相关性分析情况

2 CNN-BiLSTM网络结构

2.1 CNN网络

卷积神经网络(Convolutional neural networks，CNN)是一种前馈神经网络，具有参数共享和稀疏连接两大特点，可以有效捕捉原始数据的特征。与传统的神经网络相比，它引入了卷积层和池化层。对输入数据进行压缩，通过卷积运算提取重要特征。最大池化层的目的是通过减小特征映射的大小来获取特征，降低计算成本。图4是CNN的结构。

图4 卷积神经网络结构

卷积层与输入特征进行卷积，通过滤波器生成特征映射。卷积运算可以表示为：

其中,f、k、u和*分别是得到的特征映射、卷积核、输入特征和卷积算子。偏差和激活函数由b和φ表示。激活函数在多层神经网络中发挥非线性映射作用，可在历史风数据的时空特征与预测值之间建立复杂的函数关系。

2.2 BiLSTM网络

LSTM 模型利用前向信息来预测后续信息，双向LSTM 在LSTM 的基础上，结合输入序列的前向和后向信息来提高预测精度。对于某一时刻的输出，前向LSTM 层有当时及之前的输入序列信息，后向LSTM层有当时及之后的输入序列信息。两个LSTM 层的输出向量可以通过相加、平均或链接的方式进行处理。水平方向同时计算每个时间步t的正向LSTM隐藏向量和反向LSTM隐藏向量垂直方向表示从输入层到隐藏层再到输出层的单向流动。本文采用连接两个隐态的方法，得到Bi-LSTM 模型的最终预测结果，如式⑶～式⑸所示。

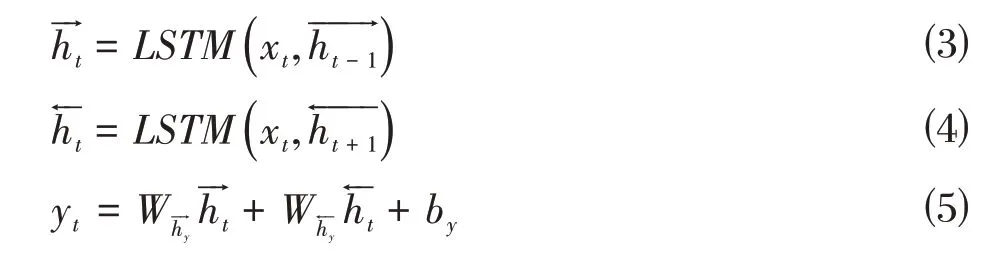
其中，LSTM(·)表示LSTM 函数分别为正向LSTM 的权重和反向LSTM 的权重，输出层的偏置用表示。Bi-LSTM的网络结构如图5所示。

图5 双向长短期记忆网络结构

3 基于CNN-BiLSTM的风电功率预测

CNN-BiLSTM预测模型

针对风电功率时间序列的随机性、非平稳性，本文提出了一种基于CNN-BiLSTM 风电功率预测方法。

模型预测步骤如图6所示。

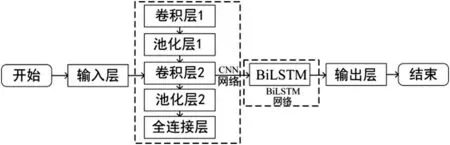
图6 CNN-BiLSTM模型结构

模型中每层的叙述如下。

⑴输入层 对长度为n的历史风电数据进行预处理，将其作为模型的输入，表示为

⑵CNN 层CNN 层的作用是提取历史输入序列的特征。此模型的CNN层设计为二层卷积层、二层池化层与一层全连接层。卷积层均为一维卷积，池化层均为最大池化方法。全连接层把处理之后的数据输出，该层使用Sigmoid 激活函数。CNN 层的输出Hc=[hc1…hct-1…hct…hcj]T的表示如下：

其中，卷积层1 与2 的输出分别是C1和C2；池化层1 与2 的输出分别是P1和P2；W1、W2与W3均为权重；b1、b2、b3、b4与b5均为偏差；⊗是卷积运算。

⑶ BiLSTM 层 构建BiLSTM 层，以学习CNN 层输出的规律。BiLSTM层的输出ht的表示如下：

4 算例验证及结果分析

4.1 样本集与训练集的构建

通过前文对负荷影响因素的分析结果，选择风速、风向、温度、湿度、气压数据构成输入特征集合。使用的数据来自国内某风电场，选取2019年10月8日——2020 年10 月8 日的数据，采样间隔是5min，即每天有288 个采样点，共计105409 个采样点。采用2019年10 月8 日——2020 年9 月1 日的数据作为训练集、2020年9月2日——2020年10月8日的数据作为测试集。

4.2 预测性能指标选取

本文对风力发电功率进行预测，选取均方根误差（root mean square error，RMSE）和平均绝对百分比误差（mean absolute percentage error，MAPE）作为评价指标。RMSE和MAPE的公式如下：

其中，m是样本的个数；yi与分别是样本i风电功率的实际值和预测值。

RMSE和MAPE这两个评价指标可以衡量模型的预测性能。在风电功率预测中，如果RMSE 和MAPE的值越小，则代表预测值和实际风电功率值的差别越小，预测精度越高。

4.3 实验过程及结果分析

为了更好地验证所提出模型的有效性，分别使用LSTM 模型、CNN-LSTM 模型、CNN-BiLSTM 模型进行短期风电功率预测，4 种模型的预测结果分别如图7～图9所示。

由图7～图9可知，在风电功率的预测中，四种模型均能大致预测风电功率的趋势，其中LSTM 模型的性能最差。LSTM 模型处理平稳变化的风电数据的能力较弱，LSTM 模型处理急速变化的风电数据的能力较弱。CNN-LSTM 模型由于结合了CNN 和LSTM 两个单一模型的优点，因此其预测误差较小。

图7 LSTM风电功率预测比较

图8 CNN-LSTM风电功率预测比较

图9 CNN-BiLSTM风电功率预测比较

实验结果使用RMSE、MAPE 两个评价指标进行评估，结果如表2 所示，本文提出的CNN-BiLSTM 预测方法在RMSE 指标上和其他方法相比较，比LSTM、CNN-LSTM 分别提升了0.9656、0.262。在MAPE 指标上和其他方法进行相比较，比LSTM、CNN-LSTM分别提升了0.2699、0.1489。因此经过实验验证CNNBiLSTM模型相对于其他模型有较好的预测性能。

表2 不同预测模型的预测误差对比

5 结束语

为了更好的预测风电短期发电量，本文首先采用斯皮尔曼相关性分析的方法选取高度相关的指标。然后提出了一种基于卷积神经网络和双向长短期记忆神经网络的混合短期风电功率预测模型，该模型考虑了风电短期预测输入数据的明显时空特征。最后，应用各种深度学习模型进行仿真，验证模型的性能。实验结果验证CNN-BiLSTM 模型提高了风电功率的预测精度。