基于ARIMA模型与DES模型的政府卫生支出预测
金何春,李 林
(上海理工大学管理学院,上海 200093)
0 引言
进入二十一世纪来,在医疗卫生体制首轮改革的持续深化进程中,卫生事业得到了大的发展。然而,当前卫生总费用不断增长,这个问题已成为大部分国家聚焦的问题[1]。近年来,国内有学者开始研究卫生费用,丁海峰[2]、陈嘉琳[3]、王高玲[4]、于菲[5]等人通过构建ARIMA 模型、GM(1,1)模型等时间序列的方法,对卫生总费用变化趋势和构成进行预测分析,如文献[5]通过对陕西省个人卫生支出的预测,对陕西省居民疾病经济负担的变化趋势进行了指向性分析,为政府调整政策提供了数据支持。从现有文献看,有关各个省份的政府卫生支出的研究成果较少,此前,刘芹等[6]构建ARIMA 模型预测了未来六年我国政府卫生支出的变化情况,由于其只用单一模型对我国政府卫生支出进行分析,其结果可能参考性不足。
为了提高预测结果的可参考性,借助多个模型进行对比分析是一种有效的途径。于是本文以辽宁省为例,基于该省2006-2019年政府卫生支出数据,分别对其建立ARIMA模型和DES模型,对辽宁省未来5年政府卫生支出进行预测。希望经过对所得结果的对比分析,可为辽宁省相关部门优化医疗卫生政策提供较为可靠的参考数据。
1 模型构建
1.1 ARIMA模型
ARIMA模型预测精度较高,是发展比较成熟的时间序列预测模型,因此被广泛应用于卫生总费用、卫生人力资源等卫生领域的预测分析[7]。ARIMA(p,d,q)模型的实质是对原序列进行d 阶差分后,把Δdyt作为因变量所建立的ARMA(p,q)模型,其中p为自回归项,q为移动平均项。
ARIMA模型的一般表达式为:
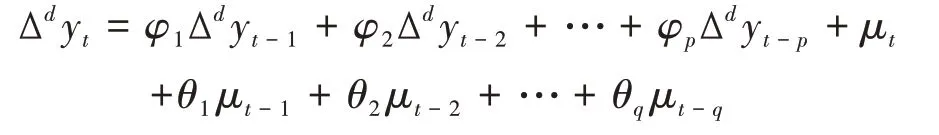
模型的建模流程:①序列平稳性检验及平稳序列白噪声检验。②模型定阶与确定最优参数。③模型残差检验。④模型预测效果评估。
1.2 DES模型
DES 模型是借助统计学中经常用于基于时间序列观察值变化趋势的指数平滑方法建立的模型,适用于中短期趋势[8]。指数平滑法分为一次、二次和多次指数平滑法,对于不同变化趋势的数据,要灵活选取进行指数平滑的次数,数据呈线性趋势时,宜使用二次指数平滑法[9]。二次指数平滑法是在一次指数平滑的基础上再进行一次指数平滑的方法,其公式为:其中为第t周期的一次指数平滑值为第t周期的二次指数平滑值为第t-1 周期的二次指数平滑值;α为权重系数(0 ≤α≤1)。
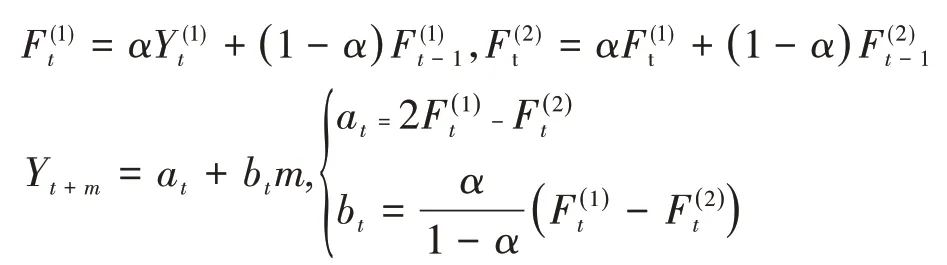
在指数平滑法中,关键参数“权重系数α”的取值一般情况下会根据经验取值或者系统自动确定。本文采用“先全局遍历再局部筛选”的方法,获得最优α值。
2 实验及结果
2.1 数据来源
本研究2006-2019年辽宁省政府卫生支出的数据来源于2015-2020年《辽宁统计年鉴》。
2.2 ARIMA模型
2.2.1 序列平稳性检验及平稳序列白噪声检验
从图1 可以看出辽宁省2006-2019 年政府卫生支出序列基本呈线性上升趋势,可初步判断原始序列为非平稳序列,由于观察法具有主观性,为进一步验证该判断,本文借助Python 编程对原始序列进行单位根检验,根据检验结果可知P 值为0.79338,远大于0.05的检验水平,故原序列为非平稳序列,需要先进行一阶差分处理,所得一阶差分序列如图2 所示。进一步检验其单位根后,得p 值约为0.00000084,小于0.05 的检验水平,说明此时为平稳序列。最终对平稳序列白噪声检验,得P 值为0.0346,小于0.05 的检验水平,则一阶差分序列为非白噪声序列,且可以确定d=1。
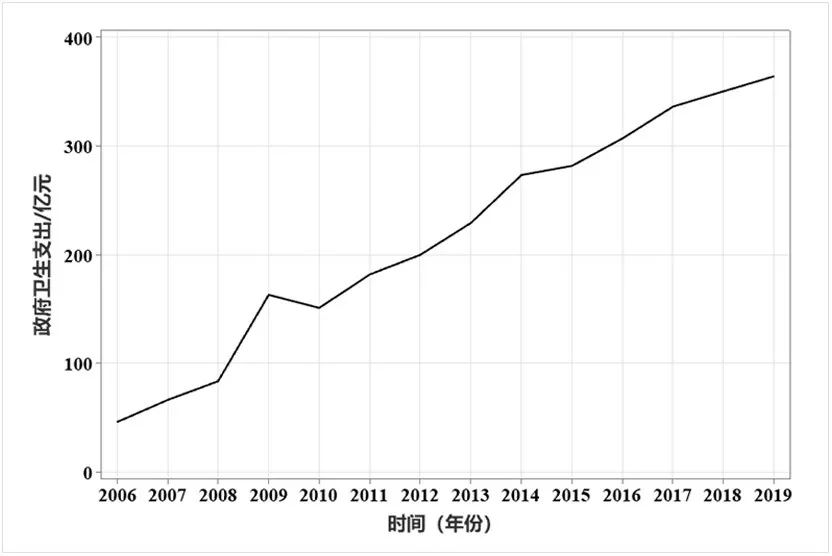
图1 政府卫生支出原始序列图

图2 一阶差分后的政府卫生支出序列图
2.2.2 模型的定阶与最优参数的确定
一阶差分序列的自相关图(ACF)与偏自相关图(PACF)如图3、图4 所示,一般情况下,可以分别观察两者的拖尾性与截尾性来选取合适的参数,但为得到较优参数,本文基于AIC、BIC 准则,在Python 下通过建立自动运算程序对ARIMA 模型的所有参数组合进行遍历,并得到不同参数组合所对应的AIC 值与BIC值,较优参数即为两者均取最小值所对应的p与q。从结果可知,当AIC 值为113.8432,BIC 值为115.5380时,得较优参数p=0,q=1。
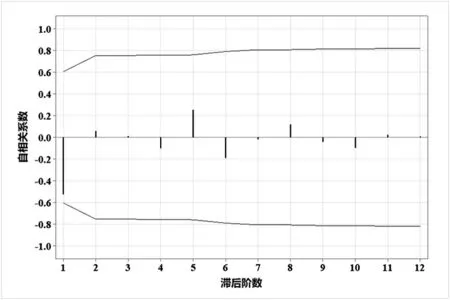
图3 一阶差分序列的自相关图
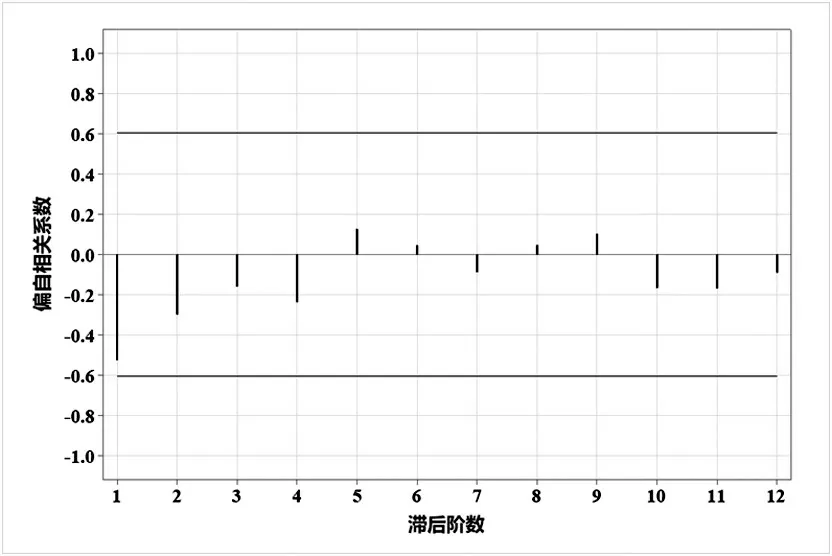
图4 一阶差分序列的偏自相关图
2.2.3 模型残差检验
模型定阶完成之后,需要对模型的残差序列进行白噪声检验,根据结果可知P 值为0.46726,远大于0.05的检验水平,这说明残差序列为白噪声,政府卫生支出历史数据中有效信息被ARIMA(0,1,1)模型充分提取,即该数据适合ARIMA(0,1,1)模型。
2.2.4 模型预测效果评估
模型预测结果如表1所示,本文采用平均绝对误差(MAE)、均方根误差(RMSE)、平均相对误差(MAPE)作为模型预测效果的评价指标。各指标计算公式如下:
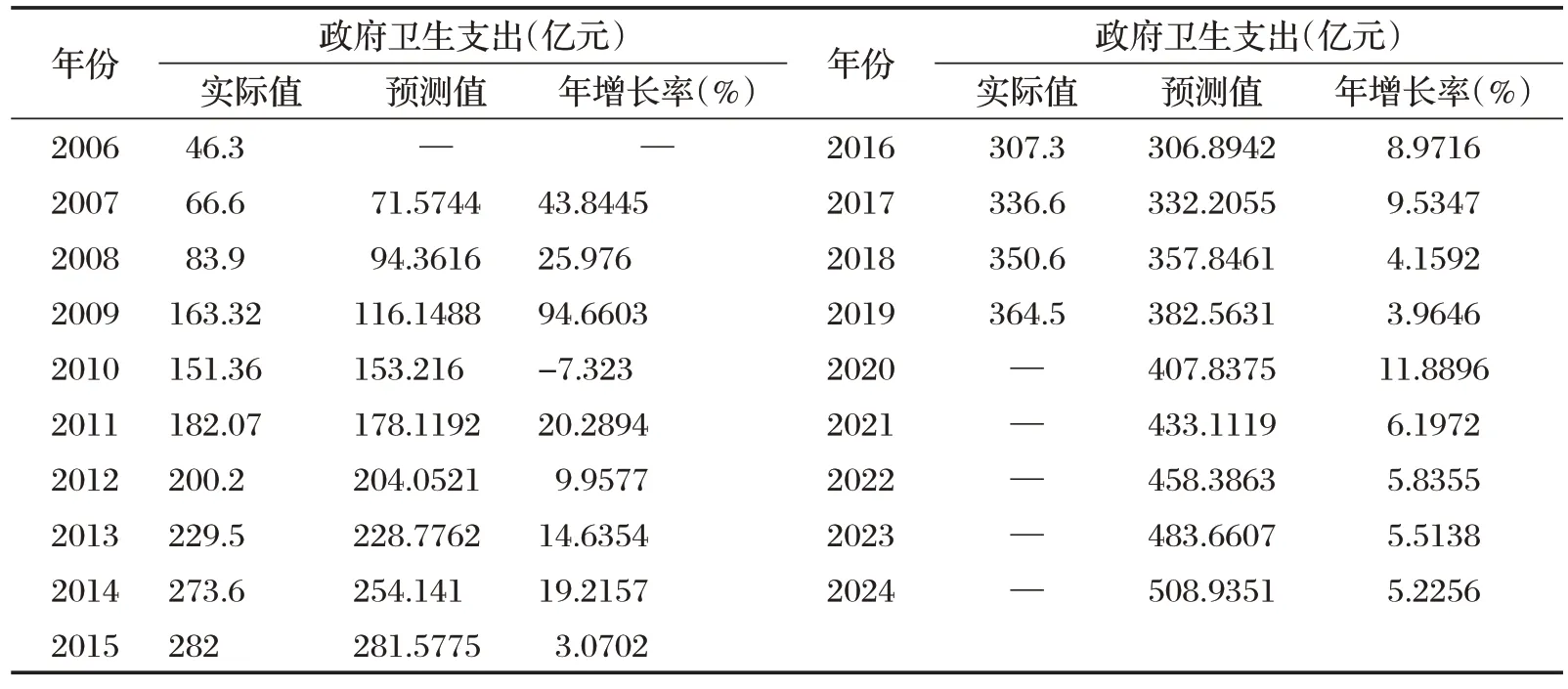
表1 ARIMA模型预测结果
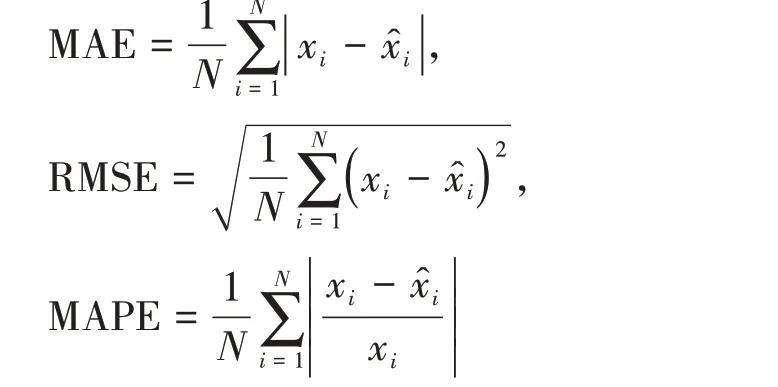
其中,为xi实际值为预测值。
经过计算得到该模型的MAE、RMSE、MAPE分别为9.46、15.6175、0.0539,三个指标的值都比较小,则表明ARIMA(0,1,1)模型可以对政府卫生支出作短期预测。
2.3 DES模型
首先运用Excel 对政府卫生支出数据进行回归分析,从拟合曲线图可知该数据呈线性上升趋势,可用DES 模型对政府卫生支出作短期预测,拟合曲线图如图5所示。其次是权重系数α的取值,先分别计算α为0.1、0.2、…、0.9时的预测值,根据实际值和预测值求出不同α对应的平均相对误差,进一步得到最优α的取值在0.4-0.5 之间,接着对0.4-0.5 之间的数依次遍历,最终得到最优α为0.44。权重系数α为0.44 时的预测结果如表2所示,并经过计算得到MAE、RMSE、MAPE分别为14.7363、25.0486、0.0828。

表2 DES模型预测结果

图5 政府卫生支出拟合曲线
2.4 ARIMA模型与DES模型预测精度对比分析
预测评价结果显示,ARIMA(0,1,1)模型的MAE、RMSE、MAPE分别为9.46、15.6175、0.0539,DES模型的MAE、RMSE、MAPE 分别为14.7363、25.0486、0.0828。两个模型的平均相对误差均低于10%,表明选择ARIMA(0,1,1)模型与DES 模型对政府卫生支出进行预测具有科学性。但ARIMA(0,1,1)模型各项误差明显低于DES 模型,说明ARIMA(0,1,1)模型预测精度优于DES 模型。ARIMA(0,1,1)模型与DES 模型预测数据与既往数据的拟合情况如图6所示。
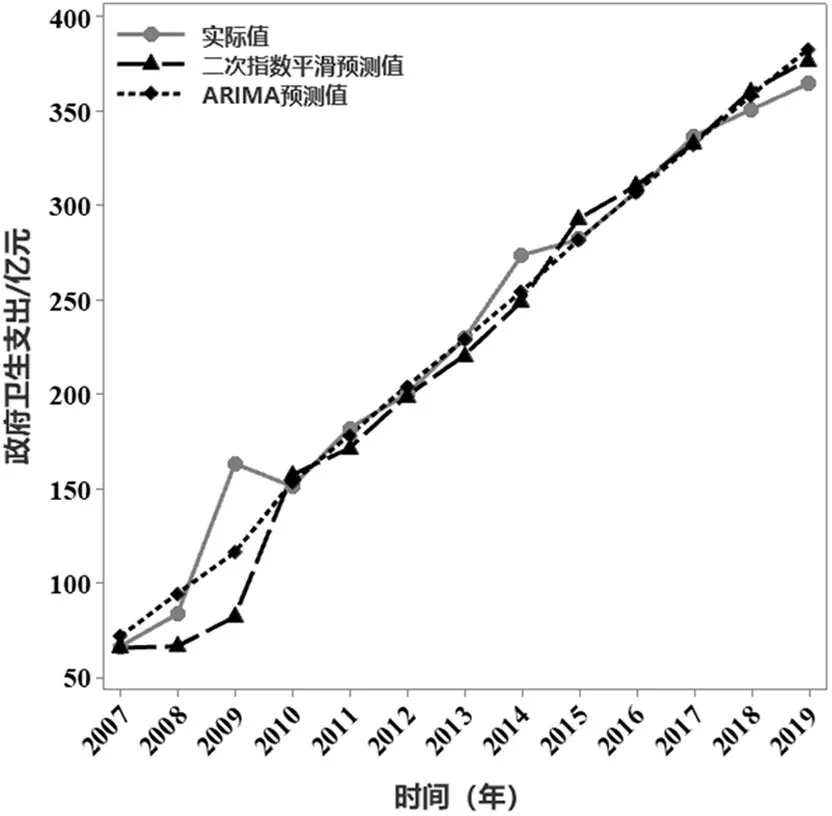
图6 两种模型拟合对比
3 结束语
本文采用2006-2019年辽宁省政府卫生支出历史数据,分别构建ARIMA(0,1,1)模型和DES 模型对辽宁省2020-2024 年政府卫生支出进行预测,通过对两者评价指标的比较,得出ARIMA(0,1,1)模型更优。根据ARIMA(0,1,1)模型预测结果可知未来5 年辽宁省政府卫生支出总额稳步提升,对应年增长率却呈现逐年下降的趋势。到2024 年,辽宁省政府卫生支出总额将达到508.9351 亿元,其年增长率可下降到5.2256%。本文所建立的ARIMA(0,1,1)模型,通过挖掘政府卫生支出历史数据的内在变化规律,实现对未来政府卫生支出变化趋势的预测。然而,影响政府卫生支出的相关变量是众多的,例如:老龄化人口数、总人口数等。因此,在上述研究的基础上,如何将相关变量对政府卫生支出产生的影响结合历史数据的内在变化规律来进行预测,从而进一步改善模型预测效果,还需要从各个层面做更深入的研究。

