基于EZW的雷达数据压缩算法
胡泽龙,杨 峰,乔 旭
(中国矿业大学(北京)机电与信息工程学院,北京 100083)
0 引言
矿井灾害是制约我国煤矿发展的重要因素,矿井地质雷达具有大小轻便、探测精度高等优势,是矿井地质超前探测的有效手段。矿井三维雷达一次扫描产生多达189 道数据,对庞大的雷达数据进行实时探测,需要对海量数据进行压缩。本文主要讨论如何对矿井三位雷达数据进行有效压缩,以解决以上问题。
近些年,学界针对嵌入式零树编码(EZW)[1]的压缩算法的研究与适配已经非常广泛。杨成林等使用改进的EZW 算法,其将主扫描和辅扫描结合并且将低频数据直接传输,实现了对声纳数据压缩[2]。王亚清将EZW 应用于医学图像压缩,使用MATLAB 实现[3]。徐锋涛等奖EZW 应用于地震数据压缩,数据压缩4 倍时,信噪比可达50dB 以上,压缩16 倍时,信噪比仍然可达30dB 以上[4]。所以EZW 算法可应用于各类行业的压缩。
本文使用嵌入式零树编码算法(EZW)进行压缩测试,并对传统EZW 算法进行优化。最后将改进算法和传统算法做对比,验证了改进算法在压缩率和压缩速度方面的优势。
1 矿井三维雷达图像特点分析
矿井三维雷达的图像数据是一系列B-Scan 的数据集的集合,A-Scan、B-Scan和C-Scan。A-Scan图像如图1(1)所示,当矿井三维雷达的天线沿着x 轴移动时,会产生一组A-Scan 数据,这一组数据组成一个二维的数据集,也就是B-Scan 数据集,如图1(2)所示;当探地雷达沿着多个相互平行的x 轴移动时,会产生一组三维的C-Scan 数据集,如图1(3)所示。由于矿井三维雷达是从多个角度探测,所以在数据层面,其是由一组B-Scan数据集组成。

图1 A-Scan,B-Scan和C-Scan
当单路探地雷达在等间隔移动探测时,可得出探地雷达B-Scan 数据,此时的数据可以理解成一个二维图像。由于雷达数据返回的每个幅值是一个带符号的16 位二进制,可以将数据拆分成两个8 位二进制,这代表着一幅雷达数据可以无损转换成两个256色阶的灰度图。雷达图像如图2 所示,这代表着一段B-Scan数据。

图2 一个雷达图像B-Scan示例
雷达图像本身是电磁波信号,横坐标代表距离x(m),纵坐标代表往返时间t(ns),文件头记录了时间窗口w(ns)、采样点数K,道间距d(m)等。采样点数K 指的是两次脉冲的时间窗口,纵坐标中往返时间t 的大小是通过时间窗w、信号采样点位置k 以及采样点数K计算的,公式如下:

2 嵌入式零树编码压缩算法
2.1 零树的概念
嵌入式零树编码是一个经典的基于小波分解的压缩算法。经过多级小波变化之后的小波系数图像,对每一个系数而言,与其具有相同相对位置的低级系数是他的子孙,从图像的低频开始一直延伸,最后可以形成一个树形结构,这个树形结构就是零树。
2.2 算法流程
⑴指定量化阈值T
最开始的量化阈值T0应该保证2T0>Cmax(,Cmax是一个小波分解后最大的系数),一般情况下T0=2n。
⑵主扫描
主扫描中,每个小波分解系数都会被扫描并判定其类型码。编码的依据如图3所示。

图3 主扫描判断依据
⑶辅扫描
系数的类型码为“P”和“N”的节点需要被更准确的记录。在主扫描进类型码判定同时要进行量化。输入区间为[Ti-1,2Ti-1],将这个区间以Ti-1+Ti-1/2为中点进行切分,切分为[Ti-1,Ti-1+Ti-1/2 ]和[Ti-1+Ti-1/2,2Ti-1]两个区间,量化的输出为1 个比特位,即输出‘0’或者‘1’。
⑷输出编码信息
主要包含本次扫描的阈值T,主扫描的类型码和辅扫描的辅编码。由于这个过程是循环进行的,所以编码和传输的过程可以同时进行。
3 适应三维探地雷达数据的改进的EZW算法
3.1 小波基的选取
一个好的小波基满足一下几个特征:①相似性,小波基选择的与雷达数据越相似,变换后的能量越集中,有利于压缩。②正则性,正则性用来刻画函数的光滑程度,正则性越强,小波基就越平滑,奇异点就越少。③紧支性,为了减少计算量,倾向选用长度小的小波基。本文选取了十余种小波基来进行综合测试,比较各类小波基的适用性。
3.2 边界问题
实际应用中,雷达数据是一段持续产生的,有限长度的数据流,如果不进行分界处理,经过小波分解的数据量会过多。为了避免实际应用中的运算阻塞问题,本文使用周期延拓的方法对数据进行预处理。
3.3 小波分解层次选择
小波分解层次越多,对信号分解的越细。与此同时,随着分解层次的增加,造成的信号位移也越多。为了探究雷达数据的小波分解层次,本文对比了1至5层小波分解后峰值信噪比变化,综合评比不同小波分解层次的适用性。
3.4 对EZW的改进
使用雷达数据测试后分析编码数据,发现其有几个问题:
⑴ EZW 是面向传统RGB 图像的,传统的EZW图像处理过程是将RGB 颜色空间转换为YCbCr 颜色空间,然后对YCbCr 图像进行色彩采样,随后将三个矩阵送入编码器。因为雷达数据特性不同于传统RGB 图像,可以理解为只有一个的灰度矩阵,所以可以省略另外两个矩阵处理。
⑵每轮扫描得到的类型码的最后有大量零树根类型码“T”,这些内容是无用的。因为每个树的末尾最后必定是有大量零树根,其信息不具备编码条件,所以可以进行省略。
⑶主扫描产生的类型码序列中,存在大量冗余连续的独立零“Z”和零树根“T”类型码,零树根出现概率为50%以上,且经常连续出现,有的轮次码流中有成百的“Z”连续出现。
本文提出了一种改进的EZW 压缩算法,能够保持EZW 的高效率的特点,同时可以适应雷达图像算法,改进的EZW算法的具体改进有以下三点:
⑴针对雷达数据特征,对一张输入图片只保留一个灰度的矩阵进行处理,省略其他两个颜色区间。
⑵对于每一次主扫描最后的的类型码为“T”的编码予以省略。
⑶针对大量类型码冗余的情况,引入四个新的编码。随后,针对这八种编码,引入霍夫曼[5]编码来对他们进行重新的算术编码。由于霍夫曼编码是一种无损编码,在这个处理阶段不会影响图像质量,采用这种方式可以在提高编码效率的同时尽可能的避免符号冗余。
3.5 算法流程

图4 改进的EZW的系统流程图
4 实验结果和分析
4.1 压缩倍数随着扫描轮次变化
从客观角度出发,扫描轮次(n),压缩比C进行比对,压缩比越高,证明压缩后的文件越小。C的定义如下:

其中,n 为压缩前的数据量,m 为压缩后的数据量。取一次测试的扫描轮次与两种算法的压缩倍数得到表1内容。

表1 随着轮次变化的压缩率变化表
从表1 中可以发现随着扫描轮次增加,压缩倍数逐渐减小,改进型EZW 在每轮都有不同程度的提升,在轮次较低的时候提升效果明显。
4.2 峰值信噪比和均方根误差
峰值信噪比(PSNR)和均方根信误差(MSE)是描述数据还原度的评价指标。为了探究种算法的优劣,本文计算了同组数据不同算法在不同比特率下PSNR和MSE,PSNR和MSE的定义如下:

对数据整理后,得到图5和图6,从图中可以发现,改进的EZW 算法的MSE 曲线在传统EZW 下方,PSNR 在传统EZW 上方。证明改进新算法有实质性的压缩率提升。

图5 改进EZW和传统EZW的MSE差别图
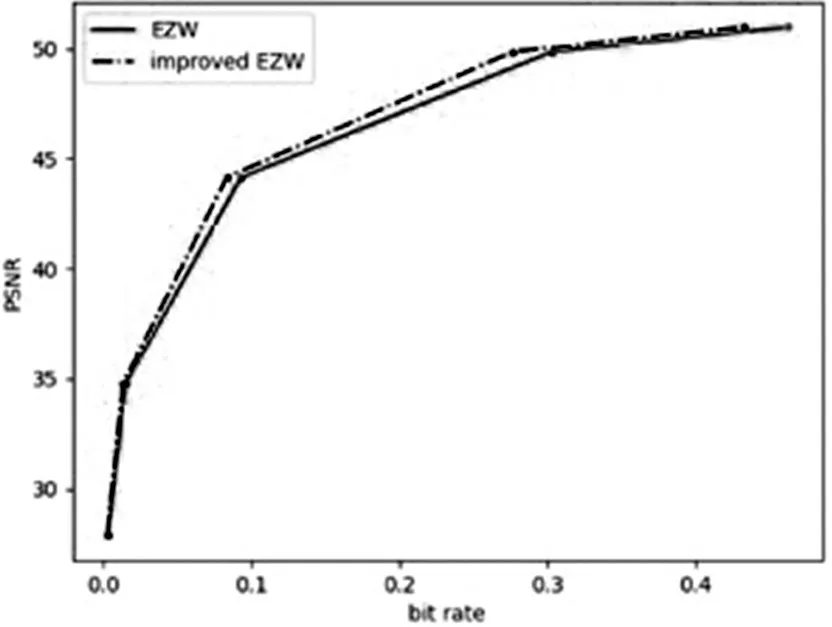
图6 改进EZW和传统EZW的PSNR差别图
4.3 运算时间
针对运算时间,统计了一次压缩的时间,并将数据绘制柱状图,得到表2内容。

表2 压缩时间提升率
由表2 数据可见,改进型的EZW 比起传统EZW具有显著的运算时间缩减,证明其效率有所提升。
4.4 基于改进的EZW的小波基的选取分析
基于改进的EZW 算法,我们使用十余种小波基进行分析,实验结果如图7 所示,从中可以发现,使用db11,sym15,sym10 效果比较好,而bior1.3,coif17,db38效果比较差。

图7 不同的小波基状态下PSNR的变化
4.5 基于改进的EZW的小波分解层次选取分析
选定了合适的小波基以后,再次对不同小波分解层次进行选择,结果如图8所示,可以知道分解层次为3级、4级、5级效果比较好,分解1级、2级效果较差。

图8 不同的小波变换层次下PSNR变化
4.6 不同方法的压缩效果的横向对比
为了验证本文选取上文中提到的几种压缩方法,使用雷达数据进行测试,得到表3。

表3 不同压缩算法的平均压缩率及峰值信噪比
从数据中可知道,使用Huffman编码、DCT变换的传统压缩方法由于其算法结构简单,运行速度较快,但是其压缩能力有限制。使用EZW 和本文改进的EZW 算法可以根据压缩要求变换运算时间,如果要求最佳压缩效果,压缩率可以达到43%,峰值信噪比为50db以上,优于前两者,具备实际使用价值。
5 总结与展望
本文采用了改进的EZW 算法对雷达数据进行压缩,省略了传统EZW 码流的冗余信息,并对码流进行二次压缩,并根据三维探地雷达数据的特性降低了计算量。实验证明,改进的EZW 算法压缩雷达数据在压缩速度和压缩质量上都超过了传统EZW 算法。并且基于改进EZW,探究了对于雷达数据适应的小波变换小波基和分解层次。
在对本文方法的深入研究中发现了存在的几点问题:
⑴并没有充分利用雷达数据中波形的时间相关性特征。实际情况中,雷达信号具有非常强的时间连续性。
⑵分析小波分析时发现,同一子带之间依然存在关联性。具体体现是高频子代也会包含低频元素。在高频子带存在的大量低值元素会增加扫描的冗余性,EZW并不能处理好这个问题。
⑶EZW 算法具有计算复杂,压缩时间相对还是较长。主要原因是零树数量多,每轮扫描需要遍历整个零树,单个零树节点扫描不具有并行性,处理依赖之前节点,所以不能使用多线程进行优化。

