工业膜建筑曲面屋顶夏季得热量分析

王 欢，高明辰、2，刘 杰，樊越胜，田国记，刘长周

(1.西安建筑科技大学，陕西 西安 710055；2.中石化南京工程有限公司，江苏 南京 210049)

1 概述

为应对频发的雾霾天气，国家逐步提高环保标准要求，尤其是针对露天堆料场引起的扬尘问题[1]。为彻底解决室外扬尘污染问题，露天堆料场有必要改为封闭式料场[2]。然而传统的封闭式料场具有建设难度大、施工期长等局限性[3]。膜结构料场是一种新型的建筑结构形式[4]，不仅可以实现传统料场的功能，而且具有跨度大、施工期短、造价低等优点[5]。将露天堆放的矿物料储放于膜建筑内，可以解决其扬尘污染的问题，符合环保、节能及可持续发展的要求[6-7]。膜结构建筑围护结构的重量只有传统建筑的30%，而且可以创造巨大的无遮挡的可视空间[8]，因此受到众多企业青睐。膜建筑热惰性小，其内部夏季的热害问题是企业担心的问题[9]。目前，国内外对膜料场相关室内得热量计算的研究报道较少。鉴于此，本文采用理论分析及编程计算的方法，对工业膜建筑的曲面屋顶得热量进行分析与计算，为工业膜建筑室内热环境的营造提供理论基础。

2 得热量组成

厂房得热主要由太阳辐射得热、对流换热、长波辐射换热、导热构成。膜材属于轻质材料，热阻较小，对热量的传递基本没有延迟，从室外通过热传导方式进入室内的热量很少[10]，所以导热得热忽略不计。

2.1 膜单元单位面积太阳辐射得热量

膜建筑曲面屋顶太阳辐射得热量主要由直接辐射得热量和散射辐射得热量组成。

① 曲面屋顶有限元划分

本文主要研究曲面屋顶，计算时若将曲面按水平投影平面进行简化，其结果会有较大误差[11-12]，因此采用有限元划分方法，对曲面进行网格划分(选取网格节点间距为0.01 m)，将其分为若干个四边形曲面膜单元(简称膜单元)[13]。假设膜单元是具有不同角度的倾斜面。

膜建筑模型见图1。原点位于模型地平面中心。膜建筑曲面屋顶拱高为4 m，竖直壁面高度12 m，跨度为30 m，长度为72 m。曲面屋顶曲面方程为：

(1)

式中z1——曲面屋顶任意点z1轴坐标，m

y1——曲面屋顶任意点y1轴坐标，m

h——曲面屋顶的拱高，m

图1 膜建筑模型

在以下计算中，南向为x轴正方向，东向为y轴正方向，垂直向上方向为z轴正方向。原点为膜建筑室内地面中心。

在空间坐标系中对曲面屋顶进行网格划分，得到四边形曲面膜单元，见图2，由此，可以得到膜单元顶点坐标。记某膜单元4个顶点为P1、P2、P3、P4，坐标分别为：P1(x1，y1，z1)、P2(x2，y2，z2)、P3(x3，y3，z3)、P4(x4，y4，z4)[14]。

(2)

膜单元各角度间的关系见图3。图中量的符号说明如下：

λ——入射角，(°)，指太阳光线与膜单元法线之间的夹角

φ——太阳高度角，(°)，指地球表面上某点和太阳的连线与地平面之间的夹角

γ——膜单元方位角，(°)，膜单元法线在水平面上的投影与正南向的夹角

ε——膜单元太阳方位角，(°)，指膜单元上某点和太阳之间的连线在水平面上的投影与膜单元法线在水平面上的投影线之间的夹角

β——方位角，(°)，指太阳光线与膜单元间的夹角

α——太阳方位角，(°)，指太阳到地面上某给定点的连线在地面上的投影与南向(当地子午线)之间的夹角

θ——膜单元倾角，(°)，指膜单元与水平面之间的夹角

图2 四边形曲面膜单元

图3 膜单元各角度间的关系

根据空间坐标系确定太阳光线向量[13]：

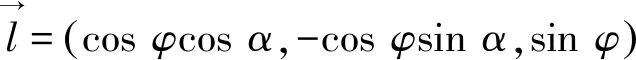
(3)

通过膜单元法向量和太阳光线向量，可求出太阳光线与膜单元间的夹角，即方位角β：

(4)

同理，由膜单元法向量和水平面法向量可得膜单元倾角θ。

② 膜单元单位面积太阳辐射得热量

膜单元单位面积太阳辐射得热量为[11]：

qi,D=EDθ(τ+η)

(5)

qi,S=ESθ(τ+η)

(6)

qi=qi,D+qi,S

(7)

式中qi，D——膜单元i单位面积太阳直接辐射得热量，W/m2

EDθ——膜单元太阳直接辐射强度，W/m2

τ——膜材透过率，取0.070

η——膜材吸收率，取0.059

qi,S——膜单元i单位面积太阳散射辐射得热量，W/m2

ESθ——膜单元太阳散射辐射强度，W/m2

qi——膜单元i单位面积太阳辐射得热量，W/m2

膜单元太阳辐射强度为膜单元太阳直接辐射强度、膜单元太阳散射辐射强度之和。某时刻曲面屋顶的太阳辐射得热量为所有膜单元太阳辐射得热量之和[11，15]。

a.直接辐射

直接辐射采用Bouguer公式[16]，对于倾角为θ的膜单元，计算如下：

EDθ=Excosλ=Exsinβ

(8)

Ex=I0pm

(9)

(10)

cosλ=cosθsinφ+sinθcosφcosε

(11)

ε=α-γ

(12)

sinβ=cosλ

(13)

式中Ex——法向太阳辐射强度，W/m2

I0——太阳常数，W/m2，取1 367 W/m2

p——大气透明系数，晴天时取0.7[17]

m——大气质量

b.散射辐射

散射辐射采用Berlage公式[16，18]。对于倾角为θ的膜单元，计算如下：

(14)

2.2 曲面屋顶单位面积太阳辐射得热量

曲面屋顶单位面积太阳辐射得热量计算式为：

(15)

(16)

q=qD+qS

(17)

式中qD——曲面屋顶单位面积太阳直接辐射得热量，W/m2

n——膜单元数量

Ai——膜单元i面积，m2

A——曲面屋顶面积，m2

qS——曲面屋顶单位面积太阳散射辐射得热量，W/m2

q——曲面屋顶单位面积太阳辐射得热量，W/m2

2.3 曲面屋顶单位面积对流换热量

由于膜建筑为全封闭，不考虑室内风速，因此，仅分析曲面屋顶与室外空气之间的对流换热。

曲面屋顶表面传热系数计算式为[19]：

(18)

式中hco——曲面屋顶表面传热系数，W/(m2·K)

A、B、n——中间变量

v——室外平均风速，m/s

室外平均风速可以直接给出，也可以按以下方法计算。

当v<4.88 m/s时，A=0.99，B=0.21，n=1；当4.88 m/s≤v≤30.48 m/s时，A=1.09，B=0.23，n=1。

膜单元位于背风面，存在：

v=0.3+0.05vf

(19)

式中vf——自由流风速，m/s

膜单元位于迎风面，存在：

当vf>2 m/s时，v=0.25vf；当vf≤2 m/s时，v=0.5 m/s。

曲面屋顶单位面积对流换热量计算式为：

qco=hco(T-To)

(20)

式中qco——曲面屋顶单位面积对流换热量，W/m2

T——室外计算逐时温度，K

To——曲面屋顶温度，K

2.4 曲面屋顶与天空间单位面积长波辐射换热量

曲面屋顶与天空间单位面积长波辐射换热量计算式为[20]：

(21)

式中qsky——曲面屋顶与天空间单位面积长波辐射换热量，W/m2

Cb——全辐射体辐射系数，W/(m2·K4)，取5.67 W/(m2·K4)

εos——曲面屋顶与天空辐射面间的辐射系统发射率，取值与曲面屋顶的发射率相同

φos——曲面屋顶对天空的辐射角系数，取1

Ts——天空当量温度，K

7:00—19:00曲面屋顶温度、天空当量温度、室外计算逐时温度见表1。

表1 7:00—19:00曲面屋顶温度、天空当量温度、室外计算逐时温度

3 膜材热物性参数

地点为西安市(东经108°56′，北纬34°18′)，夏季通风室外计算温度为31 ℃，夏季室外平均风速为1.9 m/s。研究对象曲面屋顶采用杜肯膜材，涂层材料为PVC，吸收率为7%，透过率为5%，反射率为88%，发射率为0.15。

4 得热量影响因素分析

4.1 得热量分析

① 膜建筑各壁面得热量

计算时选取夏季某典型日，当天的日序数N=207。膜建筑各壁面得热量见图4。可以看出，在各壁面中，曲面屋顶得热量最大，在12：00时占各壁面得热量之和的65%，因此有必要单独对曲面屋顶得热量的影响因素进行分析。

图4 膜建筑各壁面得热量

② 曲面屋顶得热量

曲面屋顶得热主要来自太阳辐射得热、对流换热、长波辐射换热。曲面屋顶单位面积得热量见图5，可以看出，7：00—19：00曲面屋顶得热大部分来自太阳辐射得热，曲面屋顶单位面积太阳辐射得热量占比超过50%。

图5 曲面屋顶单位面积得热量

4.2 太阳辐射得热量影响因素

① 太阳高度角

曲面屋顶单位面积太阳辐射得热量、太阳高度角随时间的变化分别见图6、7。可以看出,在一天中曲面屋顶单位面积太阳辐射得热量及单位面积太阳直接辐射得热量与太阳高度角的变化规律相同，单位面积太阳散射辐射得热量在一天中变化较小,说明散射辐射受太阳高度角影响不大。14:00时,曲面屋顶单位面积太阳直接辐射得热量出现最大值,为143.18 W/m2,单位面积太阳辐射得热量也达到最大值,为175.22 W/m2,与太阳高度角最大值出现的时间相同。因此,太阳高度角的变化是引起曲面屋顶单位面积太阳辐射得热量及单位面积太阳直接辐射得热量变化的主要因素。

图6 曲面屋顶单位面积太阳辐射得热量随时间的变化

图7 太阳高度角随时间的变化

② 曲面自身特性

曲面自身尺寸会引起曲面屋顶太阳辐射得热量变化，而曲面屋顶拱高和跨度是反映曲面屋顶几何特征的直接参数。

a.拱高

跨度取30 m，拱高分别为2、3、4、5、6 m时曲面屋顶太阳辐射得热量见图8。14：00前太阳辐射得热量随拱高增大而减小，14：00后太阳辐射得热量随拱高增大而增大。随着拱高增大，曲面相对更陡，散射辐射随拱高增大而减小。14：00前拱高越大曲面屋顶接收到的直接辐射越小，14：00后拱高越大曲面屋顶接收到的太阳直接辐射越大。但14：00后太阳直接辐射随拱高增大的程度高于散射辐射减小的程度，因此14：00后太阳辐射得热量随拱高增大而增大。

图8 不同拱高时曲面屋顶太阳辐射得热量

b.跨度

拱高取4 m，曲面屋顶跨度分别为20、30、40、50、60 m时曲面屋顶太阳辐射得热量见图9。由图可知，在拱高一定时，随着跨度增大，曲面屋顶太阳辐射得热量最大值出现时间会提前。当拱高不变时，跨度越大，屋顶的面积越大，曲面相对更平缓，能够接收到的散射辐射越大。14：00前跨度越大屋顶接收到的直接辐射越大，故太阳辐射得热量也就越大。

4.3 对流换热影响因素

西安市年平均风速为1.9 m/s。本文采用差值法在0.6～3.0 m/s范围内选取了5种风速，即0.6、1.2、1.8、2.4、3.0 m/s，计算出曲面屋顶单位面积对流换热量。为研究不同表面传热系数对曲面屋顶单位面积对流换热量的影响，假定曲面屋顶太阳辐射得热量与长波辐射换热量保持不变，只改变风速以研究对流换热量的变化规律。

风速为0.6、1.2、1.8、2.4、3.0 m/s时曲面屋顶单位面积对流换热量见图10。可以看出，随着风速增加，曲面屋顶单位面积对流换热量增加。

图9 不同跨度时曲面屋顶太阳辐射得热量

图10 不同风速时曲面屋顶单位面积对流换热量

图11 曲面屋顶与天空间单位面积长波辐射换热量及当量温差

4.4 长波辐射换热量影响因素

本文定义曲面屋顶温度与天空当量温度之差为当量温差。曲面屋顶与天空间单位面积长波辐射换热量及当量温差见图11。可以看出，单位面积长波辐射换热量和当量温差有关，当量温差越大，单位面积长波辐射换热量越大。在13：00时，当量温差达到最大值31.51 ℃，此时单位面积长波辐射换热量也出现最大值，为98.14 W/m2。

5 结论

① 曲面屋顶太阳辐射得热量占比最大，太阳高度角是影响曲面屋顶太阳辐射得热量的主要因素之一，曲面屋顶的太阳辐射得热量随太阳高度角增大而增大。

② 拱高和跨度也是影响曲面屋顶太阳辐射得热量的关键因素。

③ 影响曲面屋顶对流换热量的主要因素是室外风速，室外风速越大，对流换热量越大。曲面屋顶长波辐射换热量与当量温差有关，当量温差越大，长波辐射换热量越大。