NiCoCrAlY/YSZ梯度涂层热力学性能的有限元模拟

王士峰, 夏明岗, 刘 明, 王 玉, 王 斌, 白 宇*, 王海斗

（1.西安交通大学 金属材料强度国家重点实验室, 西安 710049；2.西安交通大学 物理学院 物质非平衡合成与调控教育部重点实验室, 西安 710049；3.陆军装甲兵学院 装备再制造技术国防科技重点实验室, 北京 100072）

热障涂层是航空发动机与燃气轮机等国家重大装备的有效热防护手段[1-2]。目前广泛使用的热障涂层一般采用双层结构，该结构由合金底层（bond coat，BC）与陶瓷面层（top coat，TC）组成，其目的是利用陶瓷面层优异的阻热性能来降低金属基体（substrate，SUB）服役时的表面温度，从而实现其在高温环境下的可靠应用。但在双层结构热障涂层中，陶瓷面层与合金底层之间的热失配应力始终是影响其可靠服役的不利因素[3]。

为缓解热失配应力，许多研究者对热障涂层进行了结构方面的梯度化设计[4-5]，在陶瓷面层与合金底层之间制备梯度层（gradient coat，GC），使得涂层在化学成分与力学性能上沿涂层厚度方向呈现梯度分布[6-7]。程西云等[8]分析了梯度层的结构形式、厚度及中间层数等参数对涂层热应力分布的影响，发现合理的梯度结构能改善涂层内部轴向热应力及剪应力分布，改变热应力分布特征。庞铭等[9]建立数值仿真模型，研究基体、黏结层及陶瓷层的厚度参数对涂层残余应力的影响，发现基体厚度对喷涂涂层的残余应力的大小和方向有显著影响。Baig等[10]制备了双层涂层和梯度涂层并进行了有限元分析，发现梯度涂层的显微组织、显微硬度和热膨胀系数均发生变化，五层梯度涂层产生的径向、轴向和剪切应力最小。Bhattacharyya等[11]利用板的弯曲理论，比较了不同基底材料的梯度涂层沉积后各层的残余应力分布，发现随着梯度层中YSZ浓度的增加，涂层的应力状态逐渐由靠近黏结层-涂层界面处的完全受拉变为局部受拉。目前学者们针对多层梯度涂层开展的研究多为梯度层的厚度、成分比例等宏观结构参数对涂层制备或服役过程中产生的热应力的影响，然而，研究使用的梯度层的热物理参数多采用解析表达式直接计算，未考虑梯度层中各相分布形态、相互作用与组分比例是否满足解析表达式的使用条件，对于梯度涂层材料形态分布的分析不够深入，缺少用于分析梯度结构涂层的高效建模方法。

本工作基于涂层扫描电子显微镜（SEM）图像，采用代表体积单元法提取梯度涂层结构特征，建立相成分比例可精确调控的梯度结构涂层分析模型，然后采用有限元方法计算不同材料成分比例下梯度层的弹性模量、泊松比、导热系数与热膨胀系数，研究涂层梯度结构与成分比例及其性能间的构效关系，进一步分析在实体结构模型中涂层的梯度结构对涂层热力学性能的影响规律。

1 梯度涂层的设计建模

1.1 梯度涂层热物理性能参数微观模型的建立

图1为等离子喷涂梯度结构热障涂层的截面SEM图与微观结构模型。图1（a）中颜色较浅的部分为YSZ陶瓷相，深色部分为NiCoCrAlY金属相，梯度层中的金属相具有起伏状的长条分布结构特征。将梯度层中金属相的不规则长条起伏结构简化为上下两条正弦结构曲线，左右两条圆弧曲线的规则长条结构，结合涂层中陶瓷相材料与金属相材料的分布规律，设计建立梯度涂层的微观结构模型，并假设[12-13]：忽略模型中的界面、孔隙、裂纹等微观缺陷，金属相的起伏特征为梯度涂层微观非均质的周期函数，涂层边界无成分波动，涂层内部各相材料材质均匀，忽略涂层初始状态残余应力。

梯度涂层微观模型的设计分三步：建立单个金属相正弦模型，计算其面积；根据梯度层中金属相与陶瓷相的成分比例，计算梯度层模型中金属相正弦模型的数量；在梯度层范围内随机生成对应数量的金属相正弦模型，得到单个相成分比例的梯度层模型；将多个相成分比例不同的梯度层模型与陶瓷面层和合金底层组合，得到如图1（b）所示的梯度涂层微观结构模型。

图1 梯度结构热障涂层 （a）显微结构形貌；（b）微观结构模型Fig.1 Gradient structured thermal barrier coating （a）microstructure morphology；（b）microstructural model

采用代表体积单元法[14]提取相成分比例不同的多个梯度层中金属相的长度，将金属相厚度方向上的起伏结构简化为正弦结构，设计高度为h，宽度为w的矩形框架，其上下边均为 θ (θ=0.5, 1.5,2.5…)个周期且相位差为0.5个周期的两条正弦曲线，垂直偏距差等于矩形的高度h，左右边均为1/4个圆弧，建立梯度层中单个金属相的正弦模型。

金属相正弦模型的矩形高度h为相成分比例x的函数，满足：

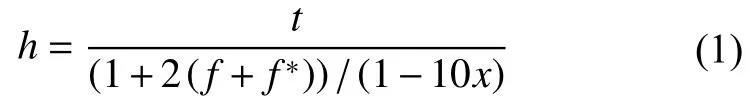
式中：t为单层梯度层的厚度；f为正弦曲线的幅值因数；f*为正弦模型间的间隙距离因数。

拟合各相成分比例梯度层中提取的金属相长条结构长度，得到金属相宽度w与相成分比例x的关系式，满足：

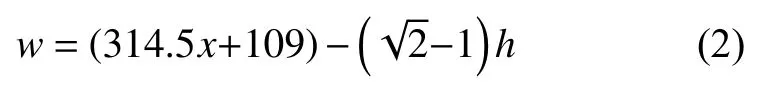
金属相正弦模型的面积S0由3部分组成，分别为矩形框架面积S1、上下边的正弦曲线面积S2和左右两侧的圆弧曲线面积S3。

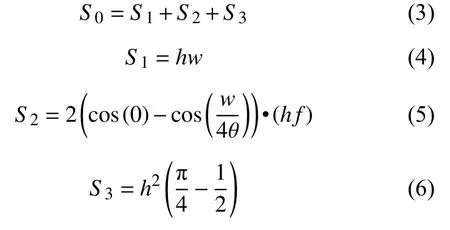
根据梯度层的相成分比例x与单层梯度层的厚度t、涂层宽度L计算梯度层内金属相面积S，令n（n为满足nS0≤S的最大整数）个面积为S0的金属相正弦模型与单个面积为的金属相正弦模型之和等于S，即得到梯度层中金属相正弦模型的数量：

根据正弦模型高度h和宽度w将梯度层划分为Nh行Nw列的均匀网格，随机在其中的n+1个网格中心生成金属相正弦模型，通过布尔运算实现金属相与陶瓷相的混合，得到单个成分比例的梯度层模型，Nh、Nw满足：

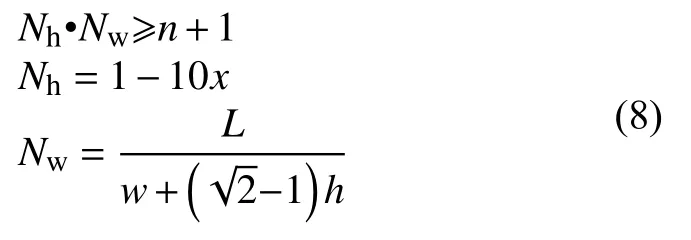
调整梯度层金属相的面积S与金属相正弦模型高度h、宽度w，重复上述设计过程，将得到的多个梯度层与陶瓷面层和合金底层结合，完成梯度涂层微观结构模型的建立。

通过有限元软件ABAQUS建立NiCoCrAlY相比例分别为0.2～ 0.8的7个梯度层的二维微观结构模型，分别添加边界条件以计算梯度层的热物理性能参数。对模型分别设置20～ 1100 ℃间的7个温度，并添加如图2所示的三种边界条件并计算：图2（a）表示涂层模型左侧和下侧所添加的位移边界条件，分别限制X方向和Y方向的位移，右侧设置Y方向的位移载荷，采用式（9）、式（10）计算弹性模量、泊松比；图2（b）表示涂层模型的上侧和下侧所添加的接触边界条件，设置环境温度和换热系数，采用式（12）计算导热系数；图2（c）表示涂层模型左侧和下侧所添加的位移边界条件，分别限制X方向和Y方向的位移，升高涂层模型整体温度，采用式（13）计算热膨胀系数。采用解析表达式（14）、式（15）计算梯度层的密度和比热。

热障涂层的热导率受涂层微观结构的影响显著，难以直接通过解析表达式准确计算，为了验证微观模型建立方法的准确性，建立厚度为1.5 mm的双层结构涂层与梯度结构涂层的有限元微观模型，并添加如图2（b）所示的温度接触边界条件，计算其在不同温度下的导热系数，采用激光导热仪（LFA 427）对 1.5 mm的双层结构涂层和梯度结构涂层喷涂样品进行热导率测试，将涂层热导率的有限元分析结果与实验测试结果对比。

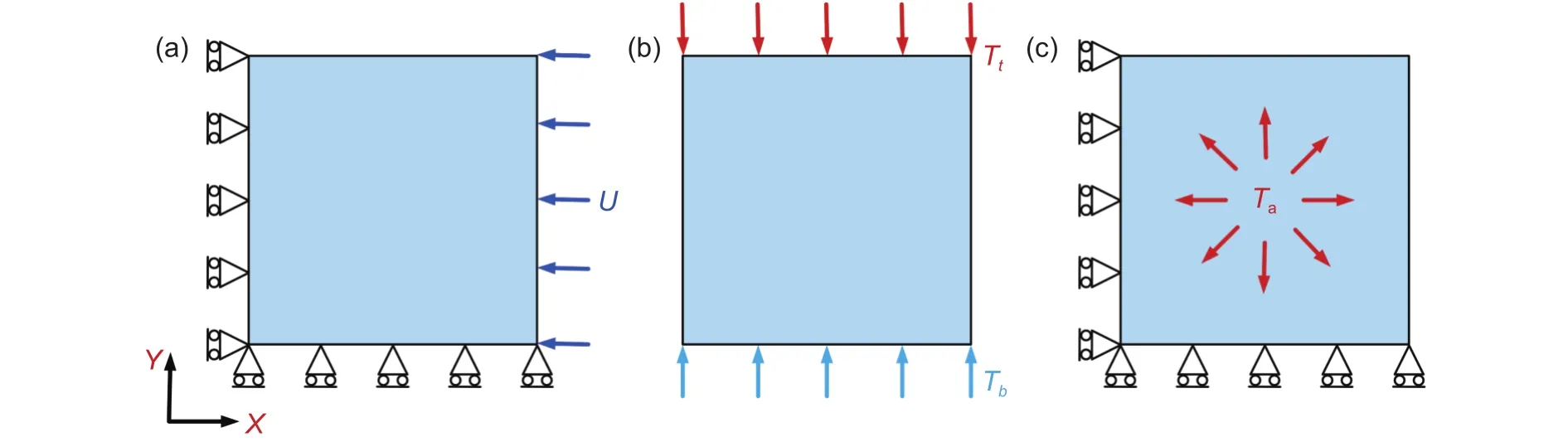
图2 梯度层的热物理性能参数分析模型的边界条件 （a）弹性模量及泊松比；（b）导热系数；（c）热膨胀系数Fig.2 Boundary conditions of thermophysical properties analysis model of gradient layer （a）elasticity modulus and Poisson’s ratio；（b）thermal conductivity；（c）coefficient of thermal expansion

划分梯度层模型的有限元网格时，由于梯度层的结构复杂，且YSZ相与NiCoCrAlY相随机分布无规则，为了得到单元大小均匀的网格，网格划分方式为自由网格，单元形状为四边形，过渡区可为三边形，传热单元与平面应力单元分别选择四节点线性四边形传热单元DC2D4与四节点线性缩减积分单元CPS4R。

表1[15-16]为已有的YSZ、NiCoCrAlY及铸铝合金的材料热物理性能参数，YSZ的材料参数大部分是通过喷涂样品进行性能测试得到，各相材料均采用线弹性模型。

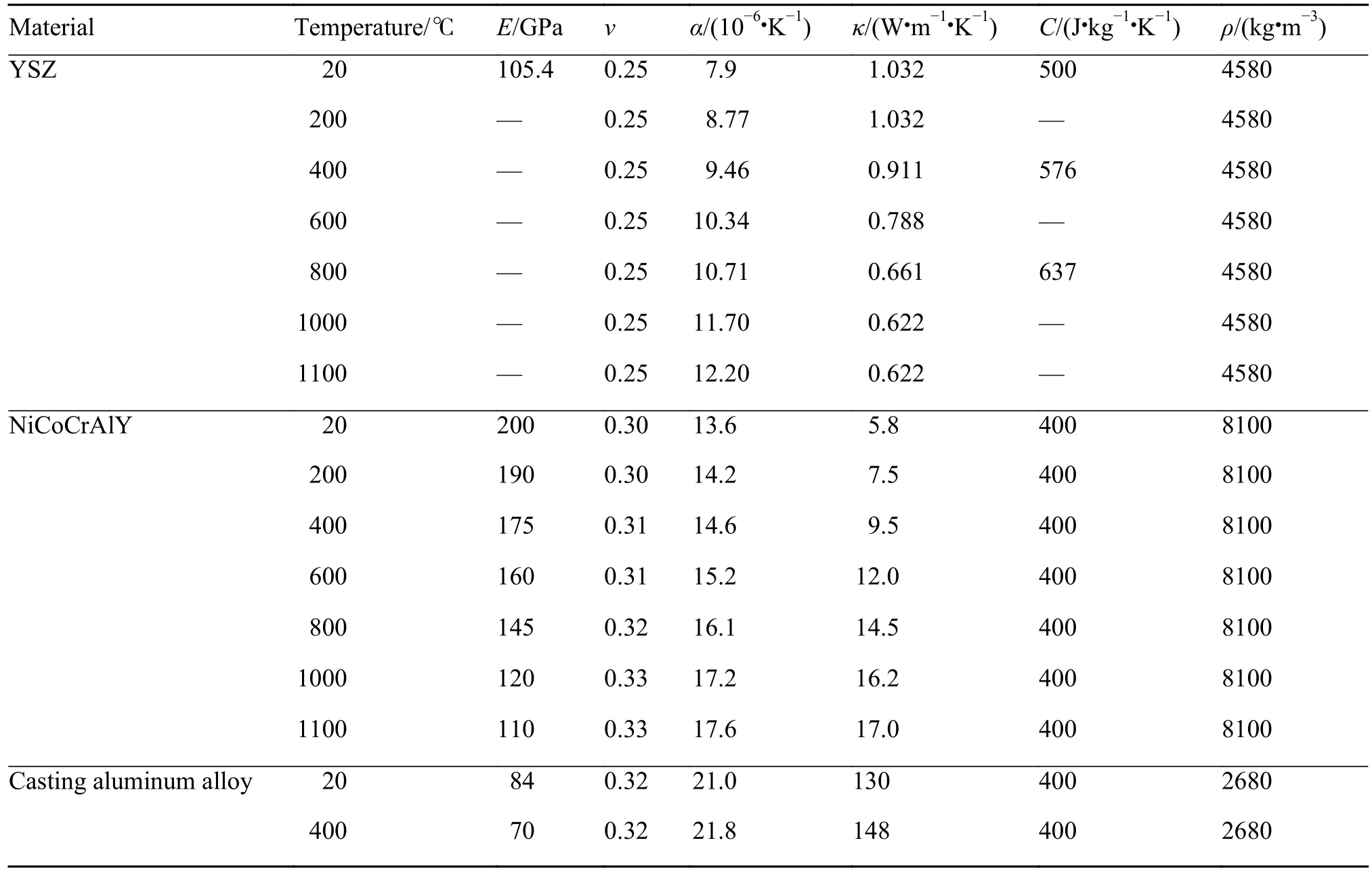
表1 材料热物理性能参数[15-16]Table 1 Thermophysical properties of materials[15-16]

弹性模量E定义为材料变形时材料在位移载荷施加方向上应力σy与应变ΔLy/Ly之比[17]：

泊松比v定义为材料变形时材料在位移载荷施加方向法方向上的应变ΔLx/Lx与位移载荷施加方向上的应变ΔLy/Ly之比：

在稳态传热条件下，根据傅里叶第一定律[18]，在长度为L，面积为A，上下边温度差为ΔT的材料截面，内部通过热量为Q时，其热导率κ可以采用式(11)计算：

热膨胀系数α定义为材料发生温度变化ΔT所导致的长度L变化：

由体积分数为VA，密度为ρA的材料A和体积分数为VB，密度为ρB的材料B组成的复合材料的密度ρ采用式(13)计算：

假设A、B两相材料之间的界面不会吸收热能，cA为材料A的比热容，cB为材料B的比热容，复合材料的比热容c采用式(14)计算：

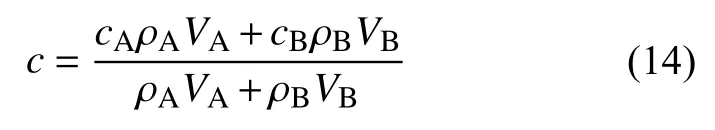
1.2 梯度涂层热循环多层实体结构模型的建立

使用有限元软件ABAQUS建立热障涂层系统的三维多层实体结构模型，分析不同涂层系统在热循环过程中的温度场与应力场，总结研究涂层的梯度结构与双层结构之间的热力学性能差异。铸铝合金基体厚度为 20 mm，宽度为 20 mm，长度为200 mm，顶面热障涂层厚度为1.5 mm，建模时独立建立各层的三维模型，通过绑定约束获得涂层系统的实体模型[19]。热障涂层具有两种结构：双层结构和梯度结构，双层结构涂层中陶瓷面层与合金底层的厚度分别为涂层总厚度的90%、10%，梯度结构涂层包括三层梯度涂层与五层梯度涂层，其中陶瓷面层、梯度层与合金底层的厚度分别为涂层总厚度的50%、40%、10%。双层结构涂层具有一种结构，梯度结构涂层的梯度层数和成分梯度不同，具有6种结构，根据其结构特点分别进行命名，如表2所示。

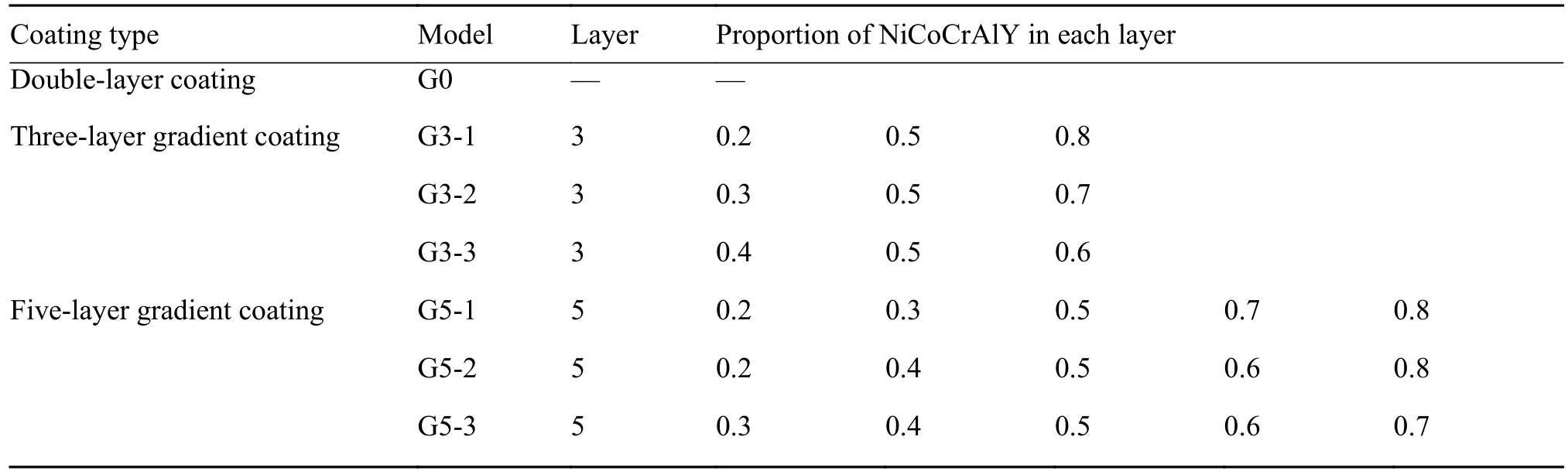
表2 双层涂层和梯度涂层的层数和成分比例Table 2 Number of layer and composition ratios of double-layer coating and gradient coating

研究对象为涂层系统在一个热循环过程中的涂层隔热性能与涂层应力状态，涂层系统的初始温度为25 ℃，热障涂层顶面接触环境温度从25 ℃升高至 1178 ℃再降低至 25 ℃，对流换热系数为1504 W/（m2·K），忽略高温气体对涂层的冲击力作用，基体底面与25 ℃的冷却空气接触，对流换热系数为 900 W/（m2·K）。

模型网格划分为四面体结构化网格，传热单元与平面应力单元分别选择八节点线性四面体传热单元DC3D8与八节点六面体线性减缩积分单元C3D8R。由于涂层厚度相对于基体厚度较小，且涂层/基体界面处存在应力集中，故需在轴向上加密涂层/基体界面及涂层的网格，并进行网格无关性验证以确定网格无关解。对梯度结构涂层模型的各部件分别设置不同尺寸的网格，计算比较涂层界面处的最大Mises应力变化量，以进行网格无关验证。验证结果如表3所示，当基体轴向渐变网格尺寸细化为100 ～1000 μm，合金底层及各梯度层网格轴向尺寸细化为25 μm，陶瓷面层网格轴向尺寸细化为50 μm时界面应力变化量较小，模型满足网格无关性要求，此时模型整体网格数量为92.4万，最终建立的涂层结构模型与网格划分细节如图3所示。

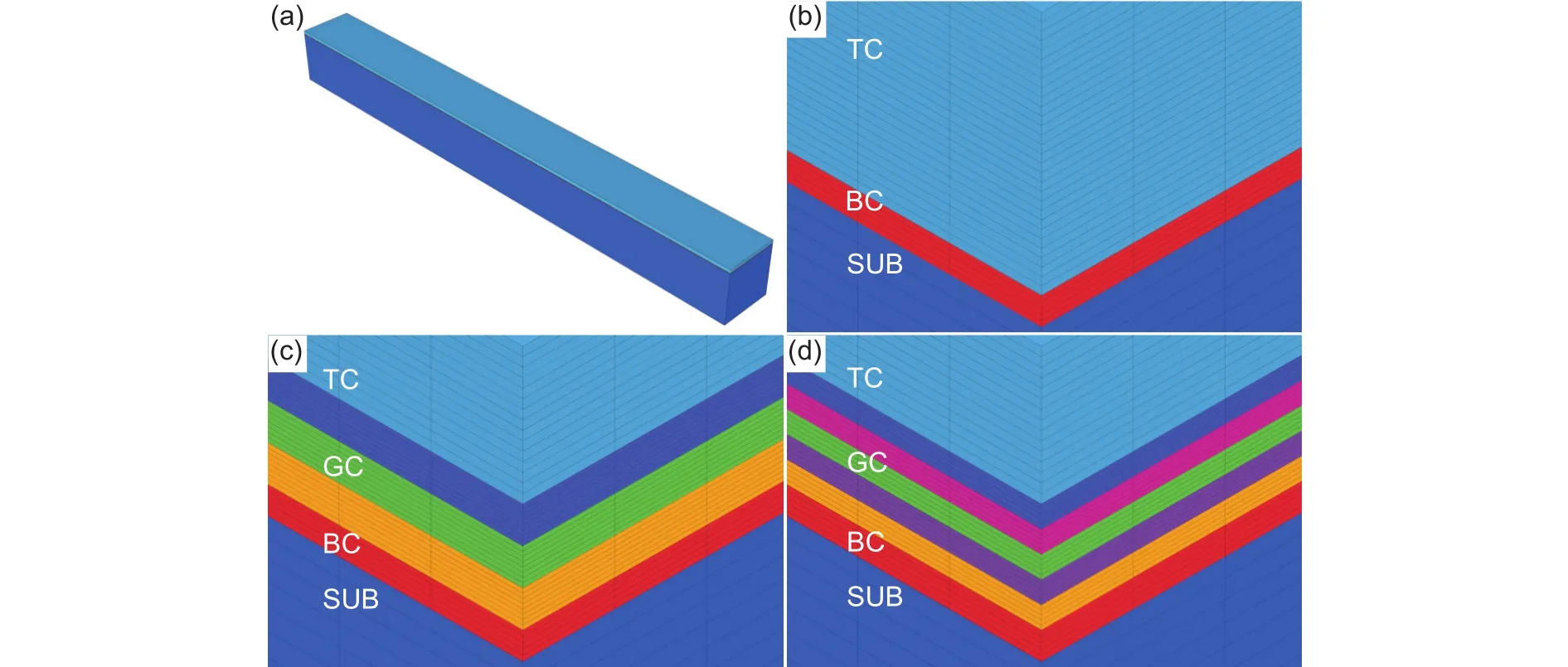
图3 涂层系统的实体结构有限元模型 （a）实体模型；（b）双层结构涂层；（c）三层梯度涂层；（d）五层梯度涂层Fig.3 Solid structure finite element model of coating system （a）solid model；（b）double-layer coating；（c）three-layer gradient coating；（d）five-layer gradient coating

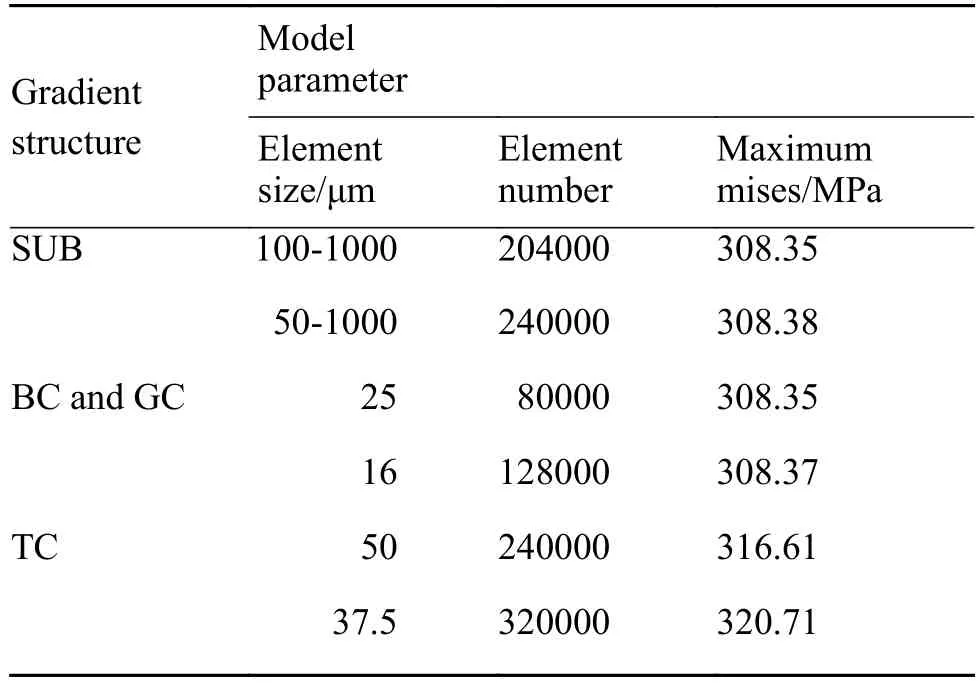
表3 网格无关性验证结果Table 3 Grid independent validation results

2 结果与讨论

2.1 梯度涂层热物理性能参数的计算结果

图4为不同NiCoCrAlY相成分比例梯度层的热物理性能参数计算结果。由图4可知梯度层的弹性模量、泊松比、热膨胀系数、比热容、密度和导热系数与其相成分比例近似呈线性关系，其中导热系数受各相分布形态的影响。梯度层中起隔热作用的主要是陶瓷相，因此随着梯度层中金属相比例的增加，其导热系数也随之增加，如图4（c）所示。当梯度层中NiCoCrAlY金属相比例较低时，导热系数增加缓慢，当相比例增长到0.7时，其常温下的导热系数达到 2.91 W·m-1·K-1，但是当金属相比例继续增加时，导热系数曲线的斜率迅速提高，这是由陶瓷材料和金属材料在导热方式差异与形态特征上的差异所导致。在梯度涂层微观模型中，各梯度层金属相平行于涂层径向分布，当金属相比例较低时，其分布较为分散，陶瓷相导热占优，涂层表现出低导热系数；金属相比例较高时，其分布较为集中，在厚度方向上金属相导热占优，涂层表现出高导热系数。

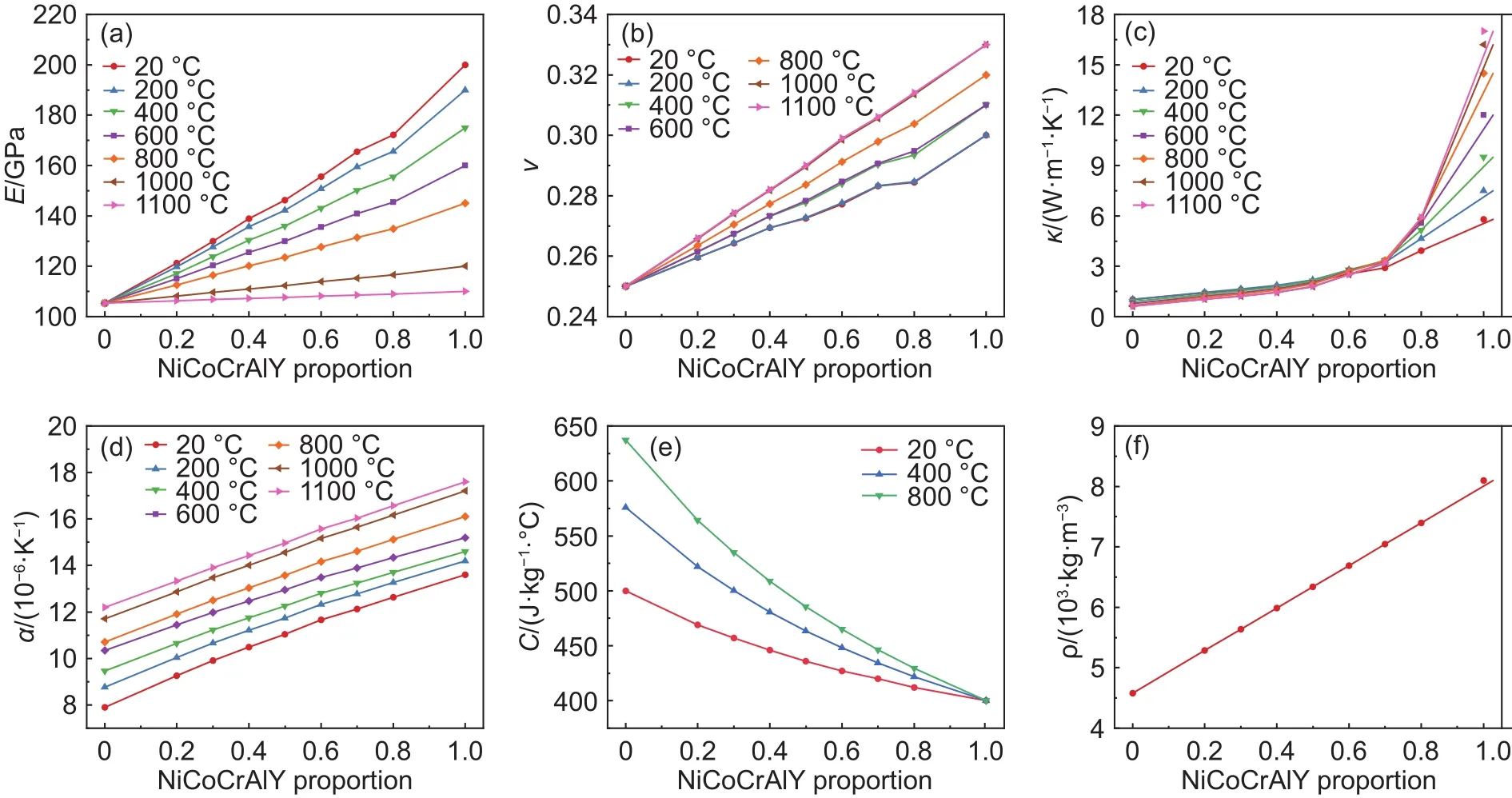
图4 不同温度下梯度层的热物理性能参数随 NiCoCrAlY 相比例变化曲线 （a）弹性模量；（b）泊松比；（c）导热系数；（d）热膨胀系数；（e）热容；（f）密度Fig.4 Variation curves of thermophysical properties of the gradient layer with different proportion of NiCoCrAlY phase at different temperatures （a）elasticity modulus；（b）Poisson's ratio；（c）thermal conductivity；（d）coefficient of thermal expansion；（e）thermal capacity；（f）density

1.5 mm的双层结构涂层与梯度结构涂层的热导率有限元分析结果与实验测试结果如图5所示。涂层的热导率随着温度升高而降低，常温时双层结构涂层热导率测得为 1.19 W·m-1·K-1，梯度结构涂层热导率测得为 1.81 W·m-1·K-1。涂层中存在的微孔洞与微裂纹对涂层的热导率有显著影响，导致有限元分析计算结果和实验测试结果间存在约为5%的误差。

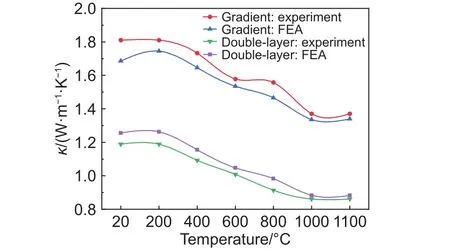
图5 涂层热导率的有限元计算结果与实验测试结果Fig.5 Finite element calculation results and experimental test results of the thermal conductivity of coating

2.2 热障涂层高温环境下的温度场分析

图6为双层结构涂层与梯度结构涂层在高温环境下的轴向温度分布与综合隔热性能对比。梯度结构涂层中的陶瓷面层、合金底层与梯度层的厚度相等，且YSZ总体积分数均为70%，因此各个梯度涂层的整体隔热能力无显著差异，只是各梯度层内部的温度场分布略有不同（图6（a））。此外，还发现涂层表层温度越高，底层温度越低，其隔热能力越强，双层结构涂层的上、下表面温度分别为949.7 ℃和440.5 ℃，梯度涂层的上、下表面温度分别为 924.7 ℃ 和 487.3 ℃（图6（b））。相较于双层结构涂层，梯度结构涂层隔热温度下降了14%。这与陶瓷相比例降低20%有关。

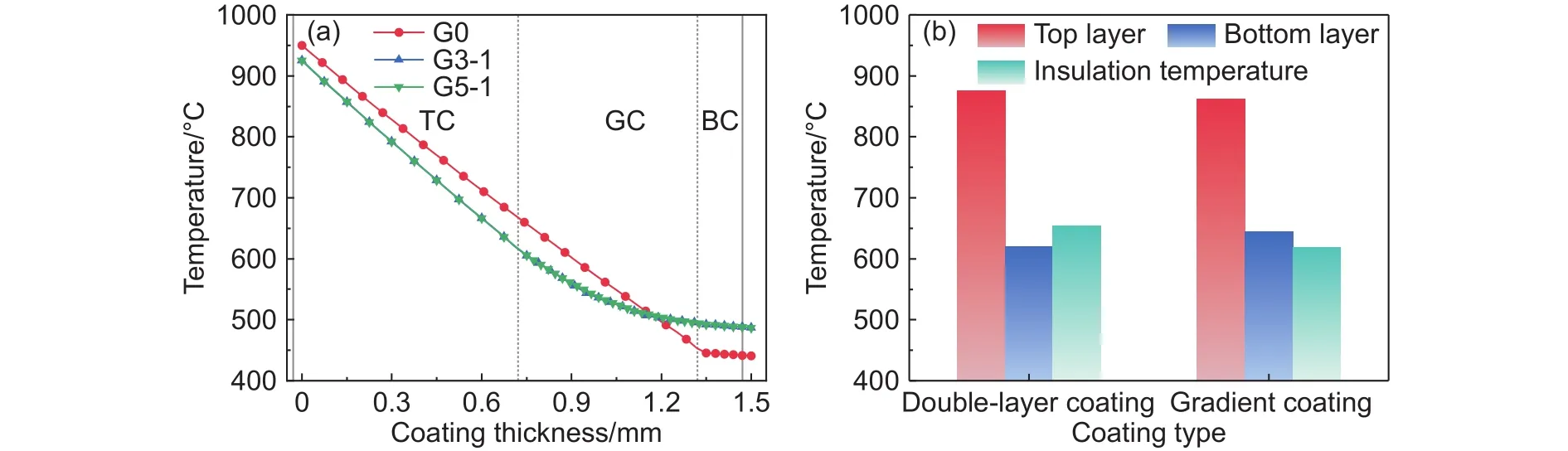
图6 不同结构涂层的隔热模拟结果 （a）涂层轴向温度分布；（b）涂层隔热性能对比Fig.6 Thermal insulation simulation results of coatings with different structures （a）axial temperature distribution of coatings；（b）comparison of insulation properties of coatings

2.3 热障涂层热循环过程中的热失配应力分析

热障涂层在热循环的过程中，由于基体和涂层的热膨胀系数不同，将发生热失配应变，使涂层在热失配应力作用下发生开裂或剥落失效，相较于双层结构涂层，梯度涂层中相成分梯度的存在使得涂层的热膨胀系数等热物理性能参数梯度变化，从而缓解涂层与基体的热失配应变，减小产生的热失配应力，有效增加涂层的高温服役寿命[20-21]。涂层中各层受到的热失配应力σc可以表示为[22]：

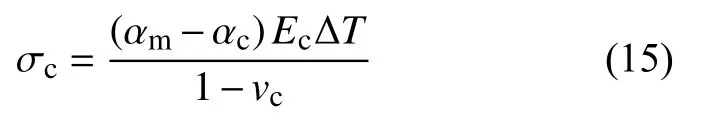
式中：αm、αc分别为基体和涂层的热膨胀系数；Ec为涂层的弹性模量； ΔT为涂层的温度差；vc为涂层的泊松比。

图7为涂层在热循环过程中合金底层产生的最大剪切应力沿涂层轴向的变化趋势。合金底层通常起到增强涂层与基体结合力的作用，其产生的剪切应力大小能够反映系统热失配应力的大小。各个涂层中合金底层产生剪切应力最大的位置均在BC/SUB界面的最外侧边缘处，沿轴向到TC/BC界面逐渐减小。高温状态下相较于双层结构涂层，三层、五层梯度涂层中合金底层在TC/BC界面产生的剪切应力分别减小22%、37%，残余剪切应力分别减小41%、52%，相同结构的梯度涂层，成分梯度越小，涂层产生的剪切应力越大。

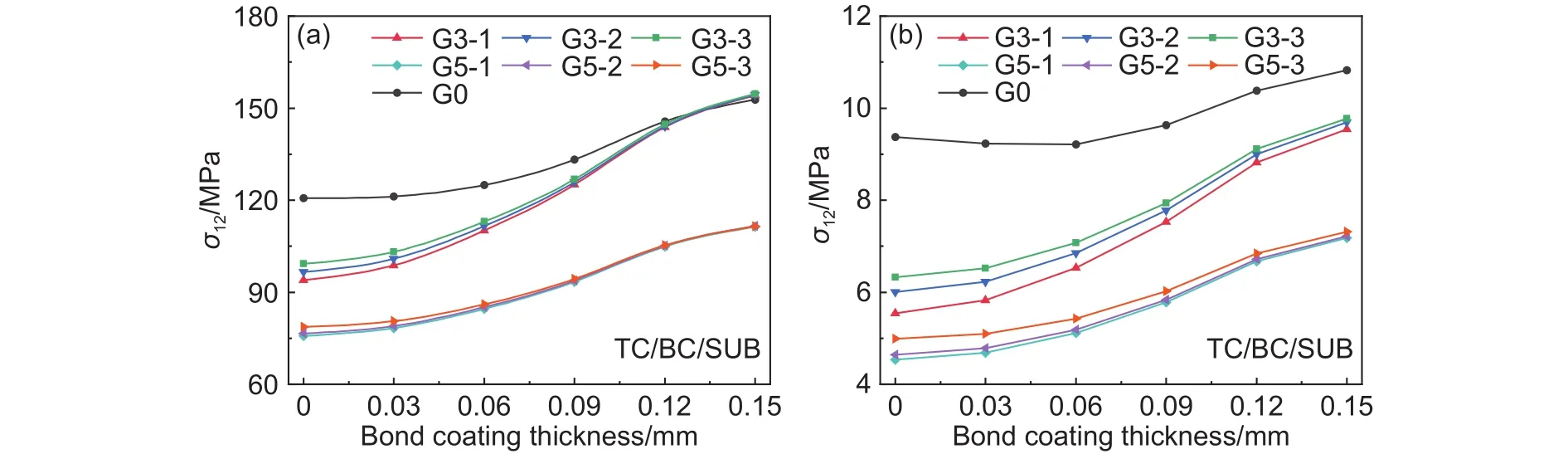
图7 不同结构涂层的合金底层产生的剪切应力 （a）高温状态；（b）室温状态Fig.7 Shear stresses generated in alloy base layers with different structural coatings （a）high temperature condition；（b）room temperature condition

图8为涂层在热循环过程中陶瓷面层产生的最大轴向拉应力。陶瓷面层产生最大轴向拉应力的位置在TC/BC界面靠近外侧边缘处，因此涂层易在该位置形成水平裂纹，这与Wang等[23]的研究结果一致。高温状态下相较于双层结构涂层，三层、五层梯度涂层产生的轴向拉应力分别减小30%、32%，残余轴向拉应力分别减小52%、59%，相同结构的梯度涂层，成分梯度越小，涂层产生的轴向拉应力越小。

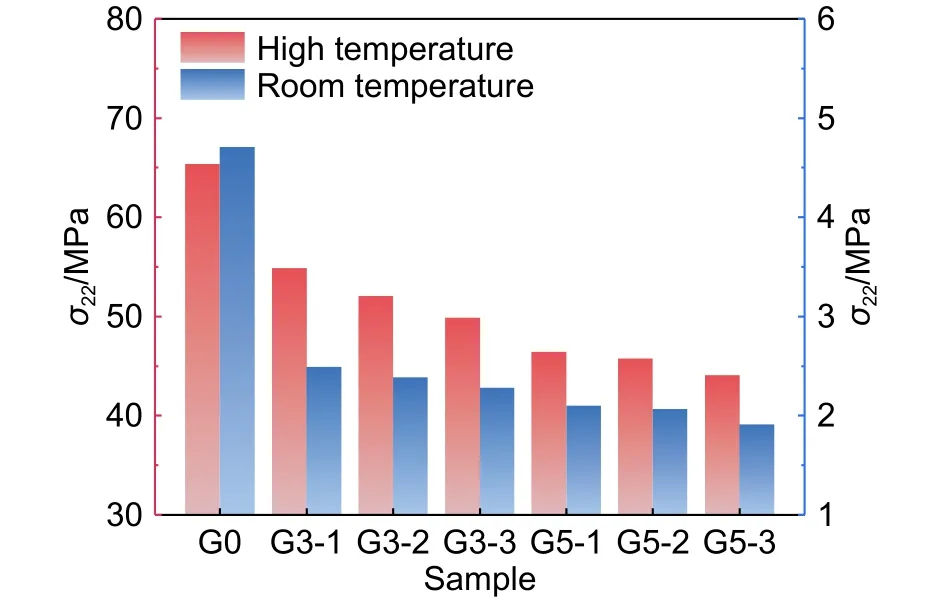
图8 不同结构涂层的陶瓷面层产生的最大轴向拉应力Fig.8 Maximum axial tensile stresses generated in ceramic top layers with different structural coatings

图9为涂层在热循环过程中陶瓷面层产生的最大径向应力以及径向应力沿涂层轴向的变化趋势。梯度涂层的应力分布比双层涂层更复杂，涂层受径向拉应力最大的位置出现于陶瓷面层在TC/BC界面的中心区域，因此该位置易形成垂直裂纹。陶瓷面层顶部受压应力，沿轴向到底部逐渐转变为拉应力，在陶瓷面层底部，高温状态下三层、五层梯度涂层的陶瓷面层底部产生的径向拉应力较双层结构涂层分别减小31%、47%。

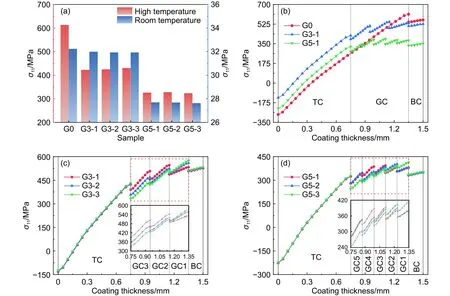
图9 不同结构涂层的陶瓷面层产生的径向拉应力对比 （a）各涂层产生的最大径向拉应力；（b）双层、三层梯度、五层梯度涂层应力分布；（c）三层梯度涂层应力分布；（d）五层梯度涂层应力分布Fig.9 Comparison of the maximum radial tensile stresses generated in ceramic top layers with different structural coatings （a）maximum radial tensile stress generated in each coating；（b）stress distributions in double-layer, three-layer gradient and fivelayer gradient coatings；（c）stress distribution in three-layer gradient coating；（d）stress distribution in five-layer gradient coating

综上，梯度层能够缓解涂层产生的热失配应力，使得涂层的径向拉应力在各层的界面处发生了突变，导致应力曲线呈上升阶梯状。当梯度结构涂层的梯度层数相同时，陶瓷面层和合金底层的成分和温度场分布相同，因此产生的径向应力大小基本相等，而梯度层产生的应力与其相成分比例有关，同一梯度层中，陶瓷相成分比例越大，产生的径向拉应力越大；各梯度层之间，材料相成分梯度越大，对应力增长趋势的缓解作用越明显，界面应力突变越大，三层、五层梯度涂层的梯度层界面应力变化值最大为11%、14%。

3 结论

（1）梯度层的弹性模量、泊松比、热膨胀系数及导热系数与其中相成分比例近似呈线性关系，其中导热系数受各相分布形态的影响。当NiCoCrAlY金属相成分比例在0.7以下时，导热系数较低，常温状态最高为 2.91 W·m-1·K-1。

（2）当梯度结构涂层中的总陶瓷相成分比例相等时，涂层的隔热性能相同。对比双层结构涂层，当梯度结构涂层陶瓷相成分比例含量降低20%时，涂层隔热温度下降14%。

（3）涂层结构的梯度化能够显著降低陶瓷面层在服役过程中内部产生的应力，实现涂层热力性能的渐变。对比双层涂层，梯度涂层高温时陶瓷面层中的热失配径向拉应力降低47%，轴向拉应力降低32%，切应力降低37%，冷却至室温后的残余应力降低50%。

（4）涂层在热循环过程中，陶瓷面层底部靠近外侧边缘处易产生较大的轴向拉应力，促使水平裂纹的形成，而陶瓷面层底部中心区域则易产生较大的径向拉应力，促使垂直裂纹的形成。