基于连续波太赫兹频域光谱系统的样品折射率测定方法
张天尧, 李博扬, 李星玥, 李 迎, 吴先毫, 赵小燕, 张朝晖*
1. 北京科技大学自动化学院, 北京市工业波谱成像工程技术研究中心, 北京 100083 2. 北京科技大学材料科学与工程学院材料物理系, 北京 100083
引 言
基于物质太赫兹介电响应的光谱传感应用在过去的二十年中得到了工业质检、 新材料研发以及医学诊断等领域的广泛关注[1-3], 一系列高质量、 可复现的太赫兹介电谱以经典太赫兹时域光谱系统(Terahertz time-domain spectroscopy, THz-TDS)为测试平台得到报道[4-6]。 以此为基础, 当前太赫兹光谱传感研究逐渐由基础物性表征向工业现场应用转变。 在工业应用领域, 传统的THz-TDS受到昂贵的飞秒激光器、 复杂的相干探测光路以及过低的光电转换效率等因素限制[7], 与之相比, 基于光混频技术的连续波可调太赫兹频域光谱系统(Terahertz frequency-domain spectroscopy, THz-FDS)具有造价成本低、 频谱分辨率高以及成谱速度快等优点[8], 而且其相干探测无需分光光路与延迟线的组合, 为实现光谱系统在工业流水线上的全光纤集成化提供了必要条件[9]。
从光谱中包含的主要信息出发, 太赫兹光谱检测应用可分为基于幅值信息的指纹吸收谱检测以及基于相位信息的折射率谱检测, 其中指纹谱吸收特征广泛应用于物质成分测定, 而折射率谱则应用于介电性质及极化率测定[10]、 聚合物成分分析[11]以及塑料制品缺陷检测[12]等。 对于传统THz-TDS, 对仪器采集的原始时域信号进行快速傅里叶变换, 即可准确获取光谱信号在频域中各频率成分上的幅值信息和相位信息[13]。 相比于已经成熟使用了近三十年THz-TDS, 新兴的THz-FDS在原始数据处理方面仍存在不足, 其频率扫描成谱过程中原始数据正比于太赫兹波到达探测器时特定相位下的幅值大小, 完成扫描后的光谱将呈现类似正弦函数振荡的形态, 其中幅值信息可通过直接对振荡信号求取包络线快速获取, 因为包络线对应的振荡极值所在的波谱成分, 是到达探测器时相位为π或者-π的太赫兹波, 对应的极值直接线性正比于太赫兹波电场强度, 包络线提取后的强度谱可直接用于开展太赫兹吸收谱表征应用[14]。 但是, 由THz-FDS相干探测机制带来的相位信息提取方法仍然处于研究阶段, 限制了相关应用的发展。 前期, 研究人员围绕如何从THz-FDS采集的原始光电流信号中提取出光谱相频特性开展了一系列研究。 Wilk[15]等提出了一种测厚算法并用于塑料制品的成像应用, 通过参考信号振荡极值点处的信号幅值与同频率处样品信号幅值之间的关系求取样品的光学厚度, 结合已知折射率获取样品厚度, 在已知厚度的情况下此算法也可用于测定折射率, 但由于信号幅值易受到样品吸收以及仪器自身噪声的干扰, 进而影响光学厚度提取的准确性。 Kong[16]和Vogt[17]等提出采用希尔伯特变换的方提取光电流信号的相位信息, 该方法计算效率较高, 但由于光电流自身振荡周期非固定值, 导致该算法在包络值提取阶段存在不确定性, 从而影响相位计算结果。 Roggenbuck[18]等从THz-FDS扫频过程中光电流信号振荡的机理出发, 对比样品和参考信号自零频点经历相同振荡周期后累积的频率偏移量求取光学厚度, 该方法计算简便, 而且可以较好地复现有吸收样品的折射率谱, 但在低频区域求取结果不理想。 针对这一问题, 本研究在上述零频基点方法的基础上, 提出了一种双基点表征算法, 对低频段光谱质量有着显著提升。
为了结合实际测试数据清晰地展开双基点折射率提取算法的介绍, 首先介绍研究工作的实验相关信息, 包括样品制备信息和原始数据采集方法。 随后结合实验数据介绍基于光混频的THz-FDS相干探测原理, 分析传统方法所存在的问题从而提出本文所建立的双基点折射率提取算法。 使用该算法对原始光电流数据进行处理, 由5个不同厚度的聚四氟乙烯样片测定的折射率为1.456±0.006, 相对误差为0.5%, 体现了算法良好的复现性。 对于同一样品, 改变积分时间和扫描步长, 由五种参数组合记录的原始数据中提取出的折射率为1.458±0.002, 相对误差为±0.2%, 验证了算法对测试条件变化的鲁棒性。
1 实验部分
1.1 样品信息
为了开展算法验证, 本文选择了在太赫兹波段没有明显吸收的聚四氟乙烯(Polytetrafluoroethylene, PTFE)作为表征对象, 根据以往THz-TDS的测定报道[19], 其折射率在0.3~3.0 THz范围内稳定在1.45±0.01区域内, 平滑的响应有利于验证折射率提取算法的效果, 聚四氟乙烯粉末购于微粉公司(Micro Powders), 型号为FLUO 625F。 纯PTFE使用压片机压制成直径为13 mm的圆形样片, 具体的制样过程在我们之前的研究中已有详细报道[10], 在此不再赘述。 为了评价折射率提取算法的效果, 制备了五个厚度不同的样片, 厚度的控制通过压片前粉末质量的等间隔增加间接实现。
1.2 太赫兹频域光谱数据采集
实验数据采集使用了基于光混频技术的连续可调太赫兹频域光谱系统TeraScan1550(德国TOPTICA PHOTONICS公司), 图1展示了THz-FDS的原理示意图。 该系统采用两个分布反馈半导体激光器作为混频光源, 两束激光器分别以1 533和1 538 nm为中心波长, 两束激光的差频位于太赫兹频段, 经过混频器形成频率在太赫兹频段的激光拍频信号。 分束后其中一束拍频信号照射到发射器端光电导天线上, 在偏置电压的作用下辐射出频率与拍频信号一致的太赫兹辐射, 太赫兹辐射到达探测器时, 以相干的形式与另一束拍频激光共同作用在探测端光电导天线上, 输出强度与太赫兹波电场幅值及相位同时相关的光电流。 发射和探测段的光电导天线均以InGaAs作为基底材料, 频率扫描通过调制激光器输出波长实现, 最小调制频率可达1 MHz, 可用频段为50~1 400 GHz, 系统中激光的传播、 混频及分束均在光纤中进行。
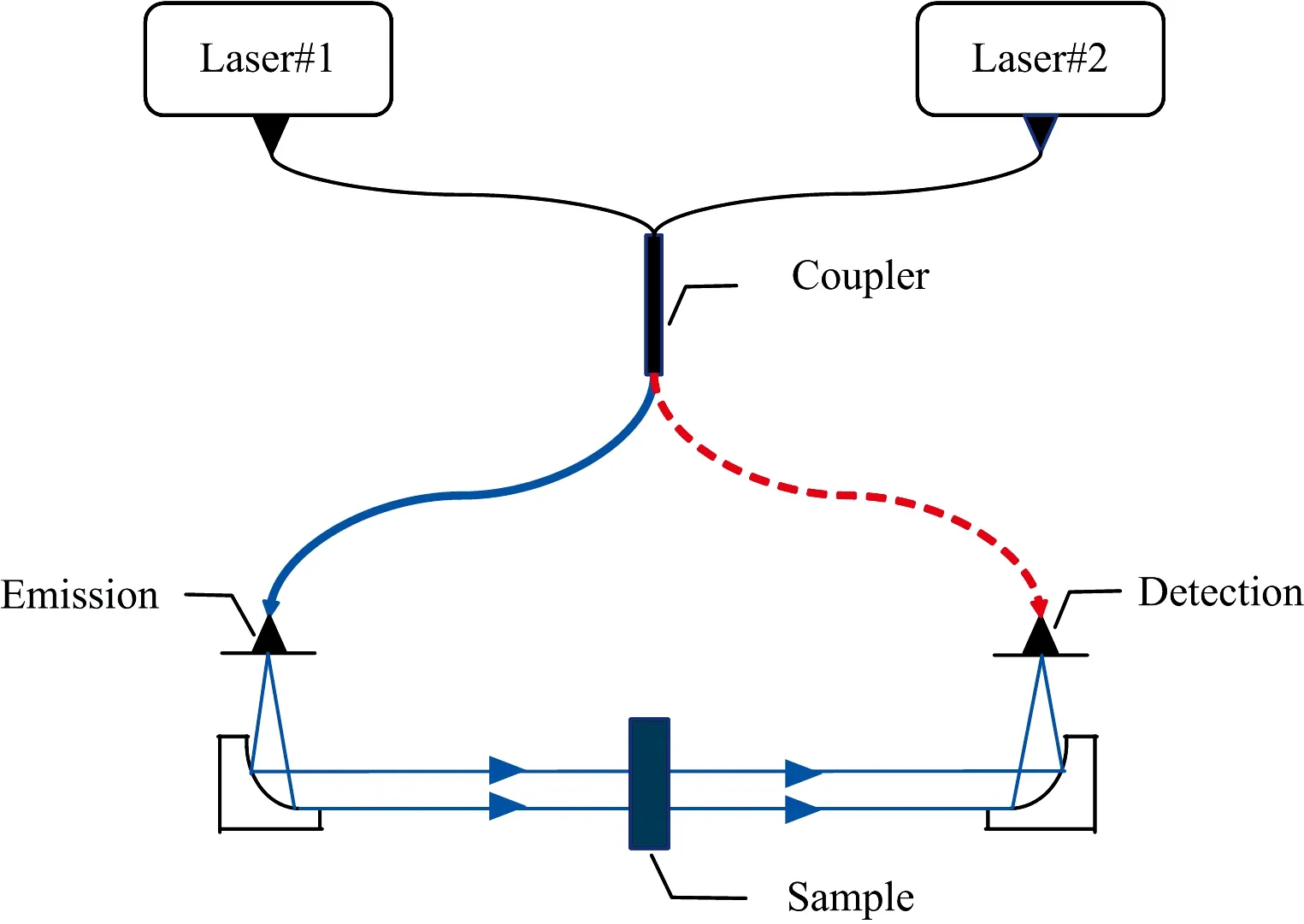
图1 基于光混频的太赫兹频域光谱系统示意图Fig.1 Configuration of a photo-mixer based THz-FDS for transmission measurement
与传统THz-TDS表征样品特性的数据采集形式一致, 每一枚样品的测试结果都包含太赫兹传播路径中放置样品前后的参考信号与样品信号, 每个样片的数据记录三次以考察实验平台的不确定性。 为了从复现性和鲁棒性两方面考察折射率提取算法的效果, 数据采集依照两种方案开展, 展示于表1, 其中复现性的考察数据来自于相同采集参数(积分时间3 ms, 频率扫描步长0.05 GHz)记录而来的五个样片的光谱信号; 而鲁棒性的考察则通过对厚度为1.91 mm的样片分别在积分时间为3, 30和300 ms步长为0.05 GHz和积分时间为3 ms、 步长为0.1和0.2 GHz的实验参数进行数据采集开展。
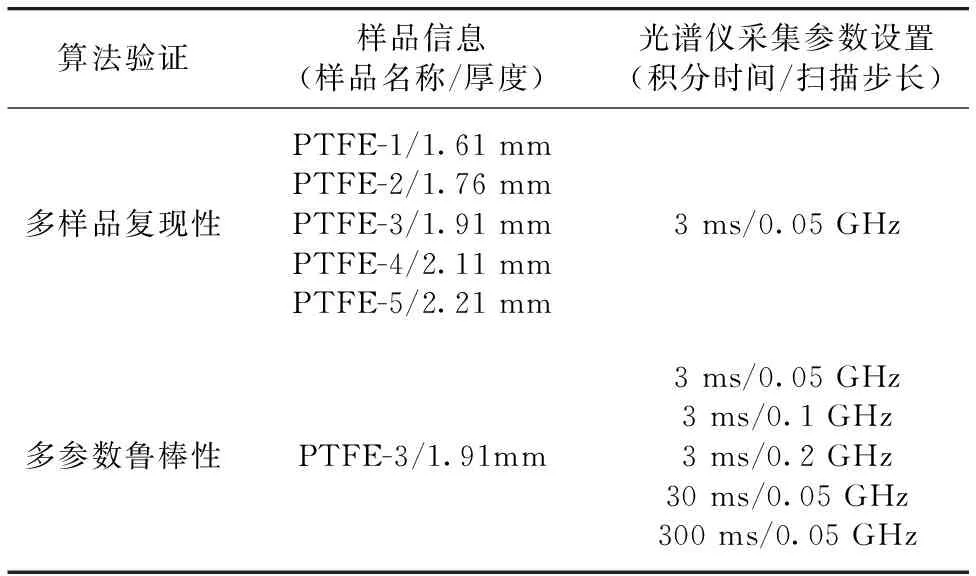
表1 实验数据采集方案Table 1 Data collection scheme for algorithm verification
根据以上两种数据采集方案记录的原始光电流数据分别展示于图2(a)和(b)。 厚度不同的样品在THz-TDS采集的原始时域数据中可以显著地观察到脉冲出现时间的差异, 但是, 由于THz-FDS具备MHz级别的频率调制能力, 因此样品厚度不同造成的相位差异在50~1400 GHz的频率范围中难以直观分辨。 选取1 015~1 040 GHz之间的光电流数据加以放大, 分别展示于图2(c)和(d)。 可以观察到图2(c)中来自不同厚度样品的光电流信号, 其振荡峰值出现的频率位置和频率间隔均有差异; 而对于图2(d)中同一样品不同采集参数获取的信号, 光电流振荡的间隔保持一致, 但极值峰位上存在1 GHz左右的偏移, 这种偏移来自于低频区域信噪比过低带来的相位误差传播。
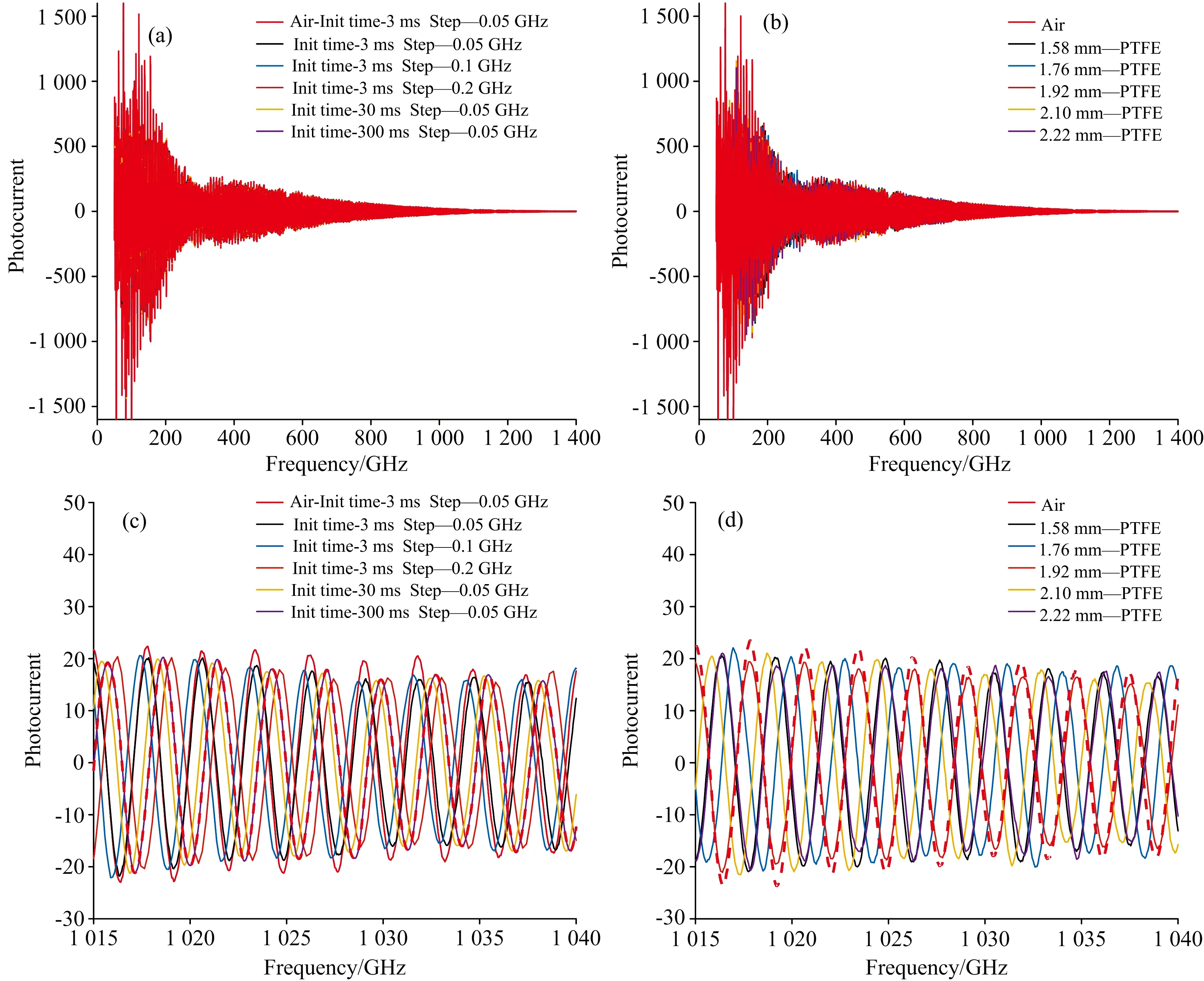
图2 由THz-FDS采集的原始光电流数据 (a)和(b)分别来自两种数据采集方案, 红色曲线为空气参考信号; (c)和(d)是放大后的局部信号用以考察相位差异在光电流信号中的呈现形式Fig.2 Raw photo-current data collected with THz-FDS(a) and (b) were recorded following two schemes listed in table 1; (c) and (d) were the enlarged details of photo-current over 1 015~1 040 GHz for a better understanding of phase delay occurred in the continuous wave
由此可见, 从THz-FDS原始数据中提取样品折射率的关键, 是将振荡极值出现频率位置和频率间隔与信号相位信息关联起来, 同时需要避免低频段和高频段信噪比过低引起的相位误差传播。 在下一章节中我们将围绕PTFE-3的实测数据展开算法理论的介绍。
2 理论模型
探测器端光电导天线输出的光电流强度与太赫兹电场幅值及相位的关系可由Idet∝Ethzcos(Δφtb)描述, 其中Ethz为频率为f的太赫兹电矢量强度, Δφtb为太赫兹波和激光拍频信号之间的相位差, Δφtb随频率变化的关系由式(1)描述
(1)
式(1)中,c为光速,l为两束激光拍频在探测器端存在的光程差, 在图1中展示为蓝色区域与红色区域之间的光学距离差, 在本系统中, 由于混频器到发射器和探测器之间的光纤长度相等, 因此,l即为太赫兹传播区域自由空间中的光学距离。
2.1 传统单基点折射率提取算法
对于相干太赫兹光谱系统, 无论是本文聚焦的THz-FDS还是经典的THz-TDS, 测定样品折射率的本质都是从光学厚度的改变引起的相位变化中提取样品折射率信息, 当样品厚度ds已知时, 折射率ns可通过有无样品时的光程差ls和lr的差值Δl进行表征, 其中Δl与ns之间的关系式为式(2)
Δl=ls-lr=(ns-1)ds
(2)
由此可知, 折射率测定的关键在于光程差的获取, 对于经典THz-TDS, 光程差可根据傅里叶变换后样品信号与参考信号之间的相位差计算得来。 而对于THz-FDS, 情况较为复杂, 其光程差的提取需要从样品光电流信号中极值点频率对比参考信号的偏移情况分析计算。 由式(1)中描述的信号相位Δφtb与太赫兹传播路径l以及太赫兹波频率f的关系可知, 当传播距离l固定时, 探测器中检测到的太赫兹波相位仍然会随频率的变化而变化, 因此探测器端记录的光电流原始信号将呈现随频率f变化而周期性振荡的特性, 如图3(a)所示, 在振荡信号中相邻的波峰与波谷之间Δφtb的相位变化为π。
由于直流成分的相位为零, 当Δφtb变为mπ时, 光电流出现第m个极值点, 对应的频率为fm, 其中fm和光程差l与相位Δφtb之间的关系式为式(3)
(3)
值得注意的是, 无论太赫兹传播路径有无样品, 式(3)都成立, 但样品与空气之间折射率的差异引起了光学路径l的变化, 从而导致相位为mπ的第m个极值点出现的频率发生偏移, 将空气与样品信号的光学路径和极值点频率分别记为lr和ls, 以及fr, m和fs, m, 结合式(3)可得
(4)
简化可得式(5)
fr, mlr=fs, mls
(5)
对于光路中存在样品时采集到的光电流信号, 其光程可表示为
(6)
式(6)中,lr可由空气光电流信号的极值点的位次数与频率代入式(3)求得; 代入式(2)可得样品光电流信号中频率fs, m处的折射率计算公式
(7)
式(7)中,lr由式(4)计算。 使用该方法计算所得的折射率谱如图3(b)所示。
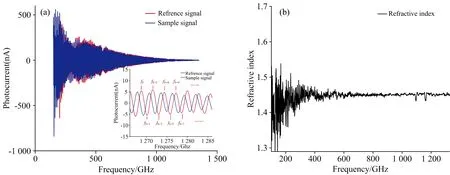
图3 (a) 光电流振荡极值点与信号相位关系图; (b) 传统零频基点法计算所得折射率谱图Fig. 3 (a) Photo-current oscillation extreme point vs signal phase;(b) Refractive index spectrum calculated by the traditional DC-basepoint method
上述折射率计算方法由Roggenbuck[18]等报道。 该方法将光电流振荡的起始点(即零频点)作为计算极值点频率偏移量累积的基点, 故第m个极值点与零频基点的频率偏移量即为该极值点频率fm。 理想情况下极值点间频率间隔应为恒定值, 但实际测得的极值点频率间隔受随机噪声的影响呈正态分布, 如图4所示。 低频段数据由于距离零频基点较近, 频率间隔中包含的频率差较少, 从而受随机噪声影响较大, 因此会导致折射率谱的提取结果波动大, 平滑度较差; 类比于多次信号采集可抑制随机噪声, 在高频区域计算折射率时, 频率差足够多, 减小了随机噪声对折射率提取的影响, 其均值更趋近于真实值, 因此, 所提取的折射率谱在高频区域内波动小、 较平滑。
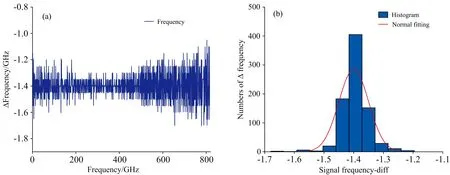
图4 相邻光电流振荡极值点频率差图(a): 相邻极值点频率差分值图; (b): 频率差的频次直方图Fig.4 Frequency difference at adjacent photocurrent oscillation extremum points(a): Plot of frequency difference values for adjacent extremum points; (b): Occurrence histogram of frequency differences
2.2 改进的双基点折射率提取算法
针对上述方法求得的折射率谱低频区域波动较大的问题,本研究提出了一种双基点折射率提取算法, 对折射率谱低频区域选择频率偏移量较大的高频区域基点计算, 而折射率谱高频区域数据选择偏移量较大的低频基点计算。 计算过程中, 首先在原始光电流信号中寻找低频区域和高频区域参考和样品信号的极值重合点作为相位差累积的两个基点f0-low以及f0-high。 对于低频基点, 假设fs, k和fr, k分别为样品和参考信号中与低频基点相隔k个极值点的信号极值频率, 相位累积均为kπ, 对应的频率偏移量分别为fr, k-f0-low和fs, k-f0-low, 如前文所述, 由相同相位累积下的频率偏移量计算fs, k处的样品折射率公式nlow(fs, k)为
(8)
与之相对应地, 使用高频基点f0-high求得频率fs, k处样品折射率nhigh(fs, k)为
(9)
式(9)中,lr为太赫兹波传播路径, 仍由式(3)计算,ds为样本的厚度。
使用两个基点求取的折射率谱如图5(a)所示, 从图中可以看出, 低频基点表征出的折射率谱高频区域较稳定, 低频区域较差; 与之相反, 以高频基点表征所得折射率谱低频区域较光滑, 而高频信号波动较大, 与预期相符, 最后在中间频段带折射率值相差最小的频率点处对二者进行组合, 从而得到高、 低频段同时保持平滑的折射率谱如图5(b)所示, 谱线中仍存在于557, 747, 996, 1 099和1 157 GHz[20]处的折射率突变源自实验环境中的水蒸气干扰。

图5 折射率频谱图(a): 低频基点和高频基点分别表征所得折射率频谱图; (b): 双基点表征折射率频谱图Fig.5 Refractive index spectra calculated with (a) single base point algorithm starts with low frequency region (red) and high-frequency region (blue); (b) dual-basepoints algorithm
综上所述, 针对THz-FDS传统零频基点算法低频区域噪声较高的问题, 提出了一种双基点折射率提取算法流程如图6所示。
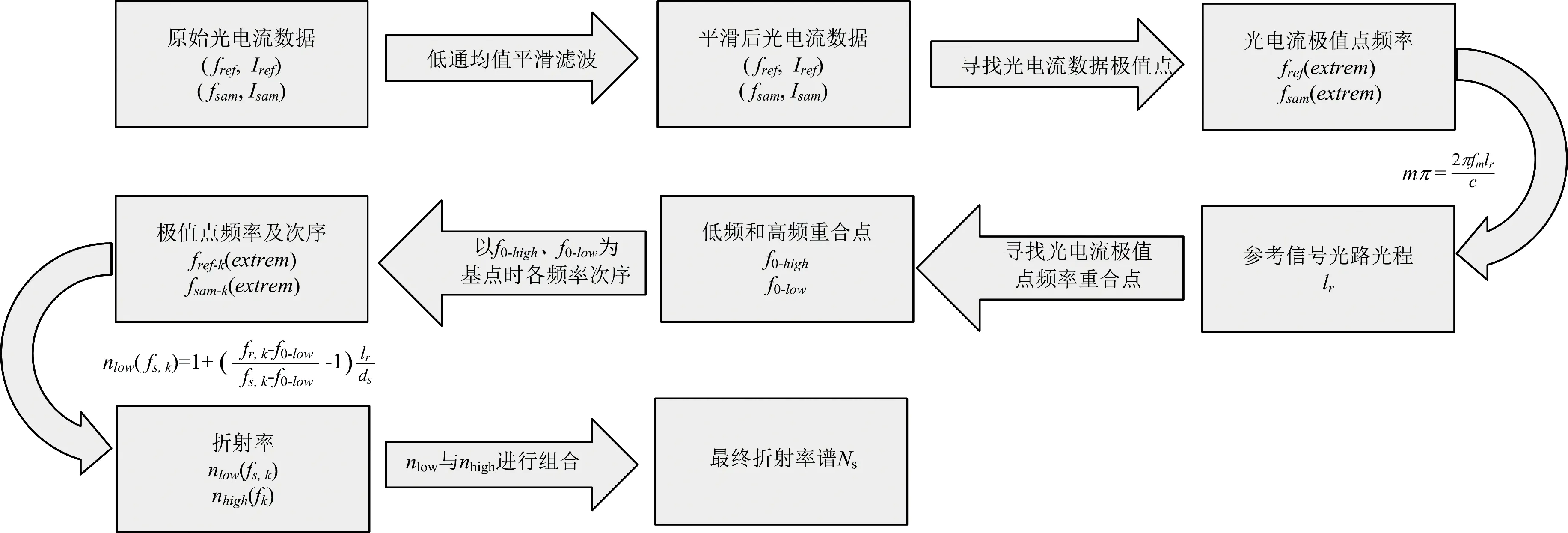
图6 THz-FDS双基点折射率提取算法流程图Fig.6 Flowchart of THz-FDS dual-basepoints refractive index extraction algorithm
3 结果与讨论
对所有样品的原始光电流数据使用本文所提出的双基点折射率提取算法进行数据处理, 复现性验证组和鲁棒性验证组的折射率计算结果分别展示于图7(a)和图8(a)。 由于PTFE在太赫兹频段折射率较为稳定, 为了进行数值化分析, 对所测频段的所有折射率取均值展示于图7(b)和图8(b)。
3.1 不同厚度样品对折射率谱提取的影响
对于复现性验证组, 图7(a)中折射率谱线来自于5个不同厚度的PTFE样品, 谱线上的误差棒表示同一样品测量三次后的结果不确定性, 谱线的高度重合充分说明了不同样品在全频段内的测定结果重复性较好且始终保持着较为理想的平滑程度, 有效改善了传统零频基点法在低频段的表征缺陷。 图7(b)中误差棒为各条折射率谱在全频段的平均值和标准差, 用以考察测量频段内折射率数值的变化情况。 5个样品的折射率平均值测定结果分别为1.451±0.003, 1.453±0.003, 1.456±0.003, 1.451±0.004和1.462±0.004, 样品间折射率均值的差异来自于厚度测量的不准确以及样品间密度的轻微差异, 组内所有样品的平均值为1.456±0.006, 相对误差仅为0.5%, 体现了本算法良好的重复性。
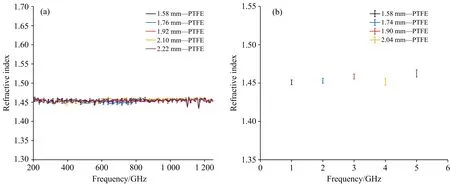
图7 (a)使用双基点提取方法处理五个不同厚度PTFE样片原始数据所得折射率谱图; (b)各样品测试频段内折射率频谱平均值Fig.7 Refractive index spectra (a) and spectral range averaged values (b) extracted by dual-base points method for 5 samples at different thicknesses
3.2 不同实验参数折射率谱提取的影响
鲁棒性验证组使用了五种数据采集参数组合对同一样品展开表征, 其中, 采样步长为在采样过程中相邻两个采样点间的采样间隔频率, 积分时间为在采样过程中采取某一频率点时对光电流的积分时长。 图8(a)中高度重合的谱线表明使用不同采样参数组合得到的折射率谱重复性较好。 图8(b)中五种采样参数组合下提取的折射率值分别为1.456±0.003, 1.460±0.004, 1.458±0.008, 1.460±0.004, 1.457±0.004, 可以观察到, 随着采样步长的增大, 折射率谱标准差有升高趋势, 可见调频分辨率的下降会影响折射率谱的测定, 与之相比, 积分时间对折射率提取影响较小。 五种参数测得的PTFE折射率平均值为 1.458±0.002, 相对误差为0.2%。 该结果表明, 对于同一样品采用不同的采样参数测定的折射率无明显差异, 证明该算法对实验参数变化具有良好的鲁棒性。
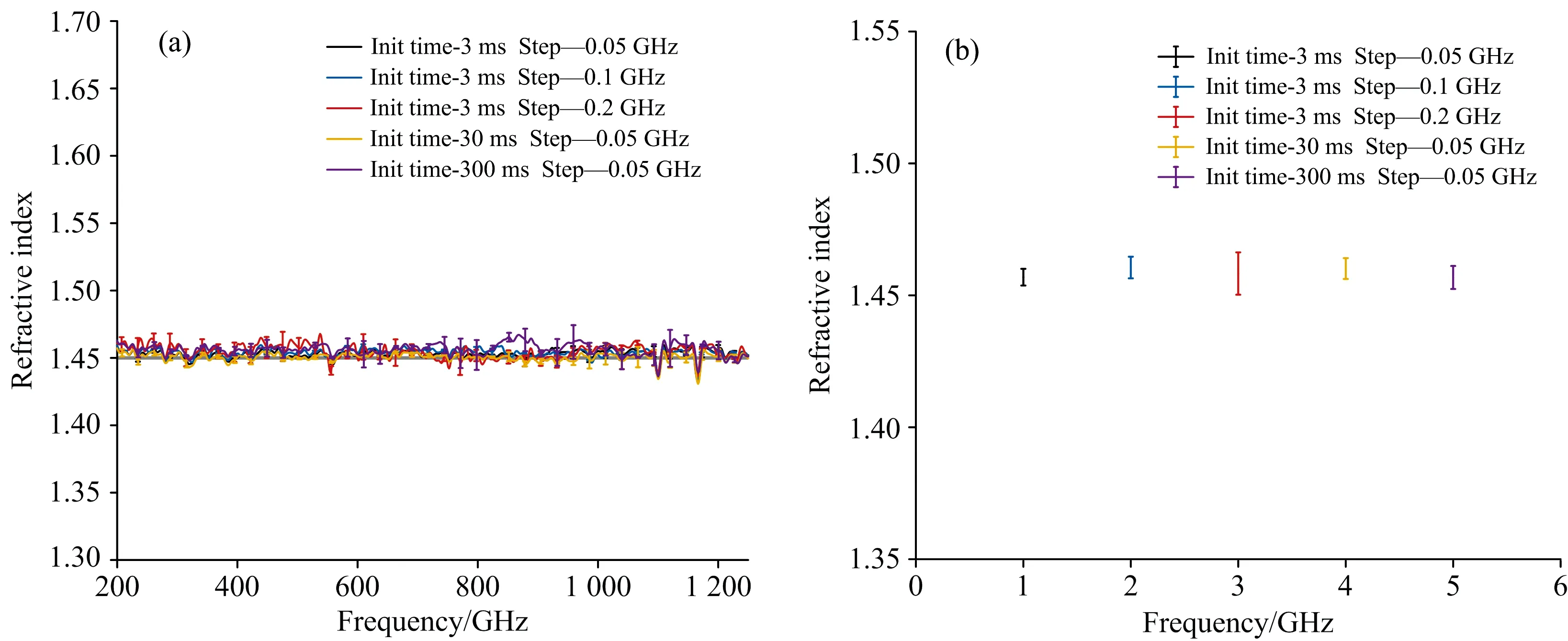
图8 (a)使用双基点提取方法处理单一PTFE样片在不同实验参数下采集的原始数据所得折射率谱图; (b)各样品测试频段内折射率频谱平均值Fig.8 Refractive index spectra (a) and spectral range averaged values (b) extracted by dual-basepoints method for one sample under different experimental parameters
4 结 论
从连续波太赫兹频域光谱系统的相干探测原理出发, 详细介绍了原始光电流数据中相位信息的呈现形式和提取方法, 分析了传统折射率零频基点提取算法在低频区域出现杂散异常信号的原因, 并提出了一种可以在测试全频带内稳定提取样品折射率的双基点计算模型, 相比于传统方法有效改善了低频段折射率谱的质量。 对于该方法有效性的实验验证, 本文从复现性和鲁棒性两方面开展。 一方面, 由1.61~2.21 mm区间内五个不同厚度的聚四氟乙烯样片的测试数据中计算所得的折射率为1.456±0.006, 相对误差仅为0.5%, 体现了算法良好的复现性; 另一方面, 对于同一个厚度为1.91 mm的样品, 改变了五种原始数据采集参数组合, 使用本算法提取的折射率计算结果为1.458±0.002, 相对误差仅为0.2%, 体现了该算法在不同数据采集方案下提取折射率时有较好的鲁棒性。
本文为连续波太赫兹频域光谱系统建立的样品折射率测定方法丰富了该系统的太赫兹光学参数表征能力, 折射率的提取是药物极化率获取、 塑料聚合物介电响应测定的基础参数, 结合连续波光谱系统在集成度、 成谱速度以及光电转换效率方面的优势, 将对太赫兹光谱技术在工业现场的实际应用起到进一步的推动作用。

