并行压缩感知计算层析成像光谱
李 虎, 刘雪峰, 姚旭日, 翟光杰
1. 中国科学院国家空间科学中心科学卫星运控部, 北京 100190 2. 中国科学院国家空间科学中心复杂航天系统电子信息技术重点实验室, 北京 100190 3. 中国科学院大学, 北京 100049 4. 北京理工大学物理学院, 北京 100081 5. 北京量子信息科学研究院, 北京 100193
引 言
成像光谱技术(imaging spectrometer, IS)集成了成像与光谱测量技术, 将空间维和光谱维数据相关联, 获取物体空间位置信息的同时得到每个像素点位置的光谱信息, 构建出空间二维和光谱一维组成的三维数据集, 称为数据立方体(Data Cube)。 成像光谱凭借“图谱合一”特性能提供目标空间分布和物质属性特征, 广泛应用于物质探测、 医疗诊断、 军事国防等领域。 成像光谱仪是应用驱动的一种成像技术, 以极快的速度发展进步, 按成像原理分为色散型、 干涉型和层析型, 按成像扫描方式分光机扫描、 面阵推扫和凝视成像方式。 常规成像光谱仪采用扫描或推扫方式遍历获取数据立方体, 这类方法适用于静态目标, 但不适用于高速成像和动态目标光谱立方体获取。
计算层析成像光谱[1](computed-tomography imaging spectrometry, CTIS)也称为计算机断层扫描成像光谱, 它结合了计算机断层扫描(computed-tomography, CT)与焦平面阵列(focal pixel array, FPA)成像光谱技术, 有效克服了常规成像光谱仪只适用于静态目标的问题, 具有高通量测量、 无运动扫描部件和性能稳定等优势, 在显微[2-3]、 空间监测[4]、 偏振[5]等瞬态应用场景领域有着应用潜力。 CTIS通过测量数据立方体经过计算生成全息图(compute generated hologram, CGH)色散元件在FPA平面多个方向和衍射级次的分光投影图像, 再使用CT算法从中重建出目标场景或数据立方体。 图1展示了数据立方体(x,y,λ)在FPA平面九个方向、 不同衍射级次按波长序形成的色散投影图像。 CT技术旨在获取物体内部分布函数, 从外部射线发射装置依据直线积分变换间接测量物体的投影数据, 运用数学模型和算法从投影数据中重构出物体内部分布。 CTIS将数据立方体看作CT技术中物体, 通过投影方式探测并从投影数据中还原出光谱和空间信息。 CTIS以拉东(Radon)变换和中心切片定理[8](central slice theorem, 又称Fourier切片定理)为理论基础, 通过直线积分构建CTIS数据立方体多个方向投影积分测量模型, 中心切片定理指出了CTIS获得的色散图中每个2D投影的傅里叶变换等于数据立方体3D频域空间的一个平面。
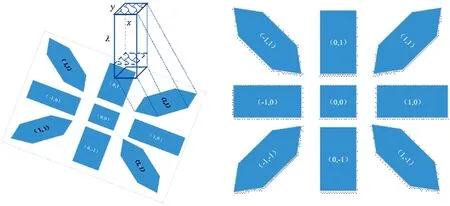
图1 数据立方体投影变换示意图Fig.1 Schematic diagram of data-cube projection
光栅型CTIS, 又称为画幅式计算层析成像光谱仪(non-scanning CTIS), 最早由日本学者Okamoto提出并将CT技术应用于IS[6], 后由美国亚利桑那大学学者Descour和Dereniak等在原理和实验基础上发展了该类型成像光谱仪[7]。 其光学原理图如图2所示, 该光谱仪主体部分由以下光学元件组成: 物镜、 准直透镜、 2D光栅和聚焦透镜。 目标场景经物镜在孔径光阑处成像并由准直透镜准直, 2D光栅色散器放置于准直光束中形成色散, 聚焦透镜最后将目标场景色散投影成像在FPA平面。 其中, 2D光栅形成不同级次光谱色散图像矩形阵列, 包括中心0级和周围更高次级衍射, 如图1所示, 以0级和±1级衍射为例, 共九个方向的色散图, 分布在FPA平面坐标系的原心、 坐标轴和四个象限中, 分别标记为(0, 0), (1, 0), (0, 1), (-1, 0), (0, -1), (1, 1), (-1, 1), (-1, -1), (1, -1)。
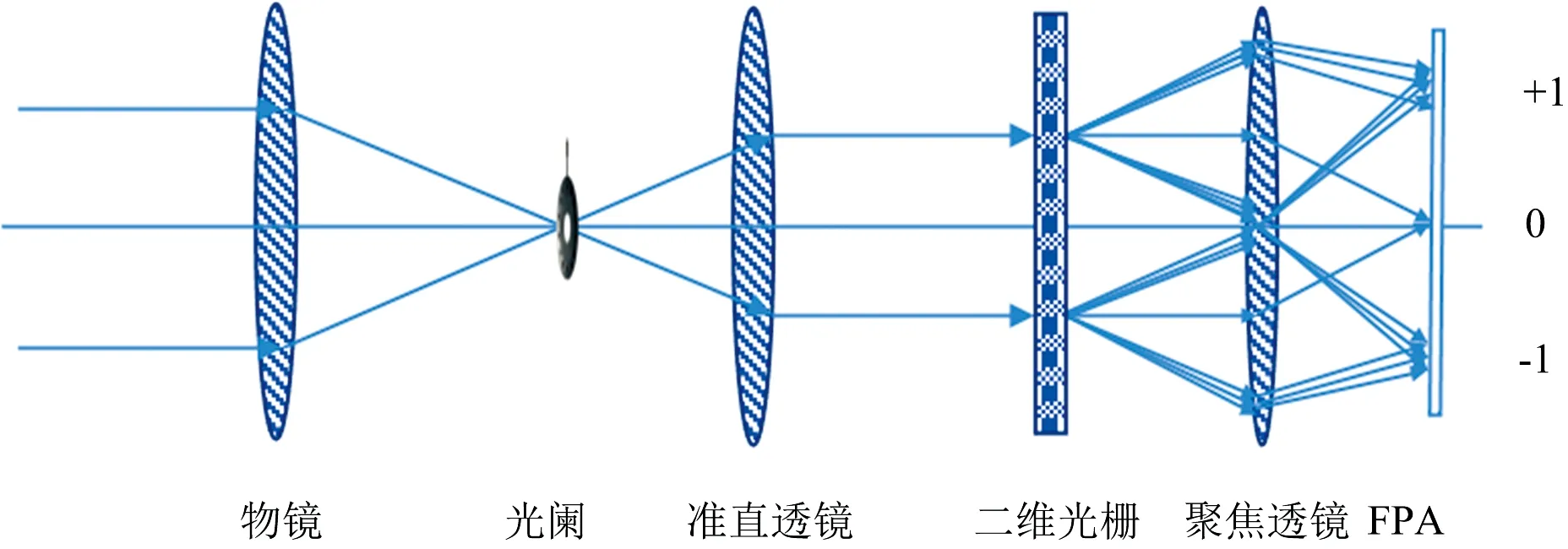
图2 光栅型计算层析成像光谱系统示意图Fig.2 Schematic diagram of raster computed-tomography imaging spectrometry system
从CTIS的分光投影采样机制和光学原理图可以看出, 其性能受限于FPA面阵探测器和CGH部件。 由中心切片定理可知, FPA面阵规模和CGH投影方向数量限定了分光投影采样范围的方位角和投影角上限, 导致数据立方体投影数据在3D频域空间的投影平面呈现失锥(Missing Cone)问题。 从CGH角度, 文献[9-10]尝试更多光栅设计方案以及旋转光栅, 文献[11]从算法角度改进重建速度。 CTIS从衍射分光投影立方体测量方式对探测器分辨率要求更高, FPA除了面阵尺寸影响投影采集范围外, 其分辨率限定了CTIS系统分光投影图像信息的采集精度, 进而限制光谱重建质量。 高分辨率的大面阵探测器(尤其是中红外、 太赫兹)造价非常昂贵, 严重限制了其实用性。
单像素相机[12-13]是压缩感知采样理论在成像领域的典型应用, 具有以亚采样的测量次数、 高通量的信号调制测量方式、 无空间分辨率的点探测器实现高空间分辨率的图像获取与完美重建的优势。 如图3所示, 并行压缩感知成像又称为分块压缩感知成像[14], 是对单像素相机成像体制的扩展, 采用面阵探测器代替单点探测器, 在空间光调制器上对目标信号进行分块独立并行的压缩感知调制测量, 提高了测量速度和系统并行能力。
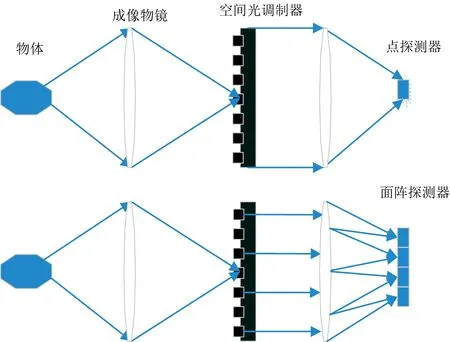
图3 单像素相机与分块并行压缩感知相机Fig.3 Single-pixel camera and block compressed sensing camera in parallel
本文将压缩感知采样理论应用于计算层析成像光谱, 建立并行压缩感知计算层析成像模型, 利用并行压缩感知技术进行采样色散投影图重建, 发挥并行压缩感知成像高分辨率成像、 亚采样及并行快速压缩成像优势, 以低分辨采样获得高分辨投影重建, 实现超过FPA性能的图谱三维高分辨投影信息快速获取, 最终实现成像光谱系统性能的提高。
1 实验部分
1.1 并行压缩感知计算层析成像光谱光学系统
本文将并行压缩感知采样方法应用于计算层析成像光谱仪的光谱立方体投影测量过程, 在传统的CTIS基础上采用空间光调制器对数据立方体色散投影快速压缩采集, 采用低分辨FPA得到高分辨色散图像, 改进CTIS受FPA性能限制的投影信号采集水平, 从而实现CTIS性能改进, 称为并行压缩感知计算层析光谱成像(blocked compressed sensing computed-tomography imaging spectrometer, BCSCTIS)。 该成像系统原理示意图如图4所示, 由传统CTIS成像系统和色散投影压缩感知成像系统组成, 具体包括以下光学元件组: 成像透镜、 二次成像透镜、 反射式DMD A、 二维光栅、 投影信号并行调制DMD B和面阵探测器CCD, 其中DMD A和DMD B分别用于逐波段逐点标定系统矩阵和并行压缩调制色散投影图像。 来自物体的光经成像透镜在DMD A成像并反射到二次成像系统, 二次成像后经二维光栅分光调制成像在DMD B并反射由CCD收集。 在系统矩阵标定过程中, 连续谱激光器作为光源经滤波器选择波段照射DMD A, 选定区域逐个打开微镜并同步记录CCD上的色散投影, 处理得到成像系统的标定矩阵; 在并行压缩调制过程中, DMD A选定区域微镜设置为全开, 调制矩阵控制DMD B对色散图像并行压缩调制由CCD同步记录压缩调制色散投影图像。

图4 并行压缩感知计算层析成像光谱仪示意图Fig.4 Schematic setup of block compressed sensing computed-tomography imaging spectrometry system
与传统CTIS相似之处是二次成像系统均由物镜、 光阑和准直器组成, 二维光栅位于二次成像系统与光谱立方体投影面之间。 不同之处是本光学系统使用了两个快速空间光调制器数字微镜阵列(digital micro-mirror device, DMD): DMD A位于成像透镜的像面, 用于CTIS成像系统矩阵的逐点精确标定; DMD B位于色散投影成像面, 用于色散投影图像的高分辨率压缩调制。
1.2 并行压缩感知计算层析成像系统模型
如1.1节所述, BCSCTIS成像模型包括传统CTIS系统和色散投影压缩感知成像系统两部分。 CTIS成像模型表示将3D数据立方体(x,y,λ)到2D投影图像的过程, 3D数据立方体和2D投影图像分别为f(x,y,λ)和g。 该投影模型表示为系统矩阵Hm和立方体f线性运算
g=Hmf(x,y,λ)+e
(1)
式中,f(x,y,λ)∈Rw×h×b,w×h为立方体空间分辨率,b为立方体波段数;Hm∈RW×H×Rw×h×b,W×H为二维投影图像的空间分辨率;g∈RW×H;e表示系统噪声。 系统矩阵Hm表示数据立方体的体素扩散函数(voxel spread function, VSF), 实验中使用逐个波长点光源标定建立。 CTIS光谱成像则是从投影采样数据g中采用重建算法恢复出光谱图像。
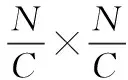
(2)
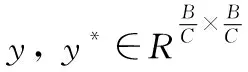
y=φ⊗x+e1,y*=φ*⊗x+e2
(3)
式(3)中,e1和e2表示互补压缩测量采集到的两次随机噪声。
由式(4)得到一对互补矩阵的测量结果Δy为
Δy=(y-y*)=(φ-φ*)⊗x+(e1-e2)
(4)
式(4)中, ⊗表示元素乘积。
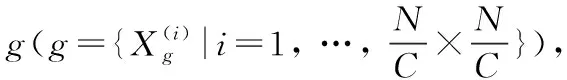
(5)
1.3 并行压缩感知计算层析成像系统仿真试验
通过仿真实验验证1.2节BCSCTIS成像模型, 处理流程包括采样数据立方体色散投影、 并行压缩测量色散投影、 重建高分辨色散投影和光谱数据立方体, 对比了直接使用低分辨探测器测量结果和基于并行压缩测量的高分辨率重建两种方法的性能。
仿真实验用数据立方体分辨率为128×128×12(128×128空间分辨率和12个波长), 按相邻波长间2像素色散距离生成436×436高分辨率2D色散投影和190 096×196 608规模的色散投影变换矩阵。 光谱色散投影仿真使用109×109低分辨探测器和4×4分块并行压缩感知采集。 以两种方法分别进行光谱重建。 其中, 低分辨采集光谱成像使用低分辨投影变换矩阵重建, 矩阵大小为118 811×196 608; 并行压缩感知光谱成像使用Hadamard测量矩阵和BCSCTIS系统模型测量和重建。
数据立方体仿真物体选自本·古里安大学跨学科计算视觉实验室(interdisciplinary computational vision laboratory, iCVL)高光谱数据集[15](BGU iCVL Hyperspectral Image Dataset, plt_0411-1155), 包括430~650 nm间隔20 nm的12个波段, 原始光谱信息如图5所示。 图6(a)为仿真得到的投影图像低分辨率探测器直接测量结果, 分辨率为109×109像素, (b)为在并行压缩感知测量系统中利用同样分辨率探测器得到的测量结果, (c)为通过BCS重建得到的436×436像素高分辨色散投影图像, 采样次数为11次(采样率11/16=68.75%)。 仿真实验光谱重建质量采用数据立方体原图与重建结果的均方误差MSE评价, 计算公式如式(7)

图5 原始光谱信息(a): 各波长光谱图像; (b): 多波段彩色图像Fig.5 Original spectral information(a): Multi-band image; (b): Multispectral composite colored image

图6 (a) 109×109色散投影图像直接测量结果; (b) 109×109压缩测量结果; (c) 436×436重建色散投影图像Fig.6 (a) 109×109 pixels dispersion projection image directly; (b) Compressed sampling image in 109×109 pixels; (c) Reconstructed high-resolution dispersion projection image in 436×436 pixels
(7)

图7对比展示了直接测量重建光谱和压缩感知测量重建光谱, 结果显示压缩感知重建光谱MSE远优于直接测量, 其全波段细节更清晰, 说明了BCSCTIS模型的有效性, 验证了低分辨探测器获取高分辨二维色散投影和高质量光谱重建的可行性。
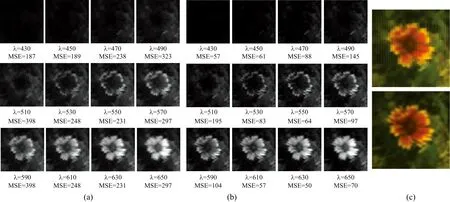
图7 (a) 低分辨采集重建光谱(低分辨率图像重建光谱); (b) BCSCTIS重建结果(压缩感知重建图像重建光谱); (c) 全波段合成的彩色物体图像(上为低分辨重建合成, 下为压缩感知重建合成)Fig.7 (a) Reconstructed spectral image from low-resolution sampling; (b) Reconstructed spectral image by BCSCTIS; (c) Colored multiple bands spectral image (the image by conventional low-resolution dispersion above, the image by BCSCTIS bellow
2 结果与讨论
实验采用计算层析成像光学实验与并行压缩色散投影测量仿真实验相结合的方式进一步验证BCSCTIS模型, 光学系统实验完成图4所示BCSCTIS光谱示意图中物体到二维光栅色散投影图像采集过程, 数学仿真完成DMD B光学并行压缩感知调制。
2.1 试验配置
光学实验使用连续谱激光器和卤素灯作为光源分别对数字物体和胶片[16]透射彩色物体进行成像光谱实验, 其中, 数字物体选用中国科学院国家空间科学中心缩写“NSSC”, 物体光谱信息包括“N”: 490 nm、 左侧“S”: 570 nm、 右侧“S”: 530 nm、 “C”: 610 nm, DMD依次显示字母并选择相应波段照射成像合成为多光谱物体; 胶片透射彩色物体印有压缩感知缩写“CS”胶片(“C”部分使用绿色滤光片遮挡, 规格为柯达Filter Wratten Red 25; “S”部分使用红色滤光片遮挡, 规格为柯达Filter Wratten Green 58), 彩色滤光片光谱透过率曲线如图8所示。
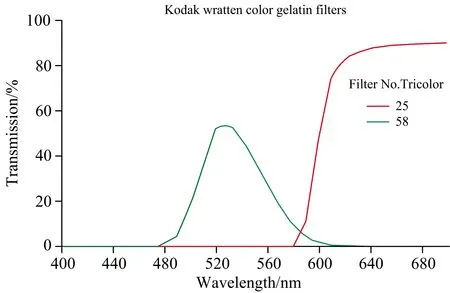
图8 柯达滤光片透过率曲线[16]红色滤光片: 25; 绿色滤光片: 58Fig.8 Transmittance curve of Kodak color filters No.25 is red filter, No.58 is green filter
系统标定使用连续谱激光器和DMD对430, 450, 470, 490, 510, 530, 550, 570, 590, 610, 630和650 nm共12个波段进行逐点精确标定, 图4所示包含了标定光路, 标定时激光器使用声光可调谐滤波器(acousto-optic tunable filter, AOTF)多通道可调滤波器逐个选波段照射DMD, 逐个翻转DMD中心区域128×128微镜, CCD同步采集每个点的色散投影。 其中, 激光器型号为YSL Supercontinuum Source SC-PRO-7; 滤波器为SuperK Select UV/nIR1; DMD为TI DLP7100, 分辨率为1 024×768, 使用中心有效区域128×128像素, 每个微镜大小为13.68 μm×13.68 μm; CCD为IMPERX B1620, 1 600×1 200像素, 使用中心有效区域950×976像素, 像素尺寸7.4 μm。
2.2 并行标定
光学实验利用了空间光调制器DMD的高空间分辨率、 快速翻转和区域可编程性, 结合连续谱激光器和AOTF多通道可调滤波器进行逐点、 逐波长系统矩阵的精确快速标定, 即完成DMD中心区域128×128像素12个波段数据立方体到950×976像素色散投影图像的标定, 将记录到的逐点色散投影图集合组织为系统矩阵, 维度为(950×976)×(128×128×12), 并以稀疏形式存储。
实验中数据立方体标定共有128×128×12个点, 受探测器帧频限制(实验中IMPERX B1620帧频通常为35 fps), 完成数据立方体中全部体素耗时很长, 严重影响实验和应用效率。 为提高标定效率, 改进系统整体性能, 本文提出并设计实现了目标区域逐点并行标定方法, 采用该方法提高了并行度、 降低了数据加载次数和加载量。 图9为同时标定P1, P2, P3和P4四个点的9个方向投影色散投影并行标定示意图。 标定算法流程如表1所示。 通过该算法, 系统标定时间可以降低到原来的四分之一。
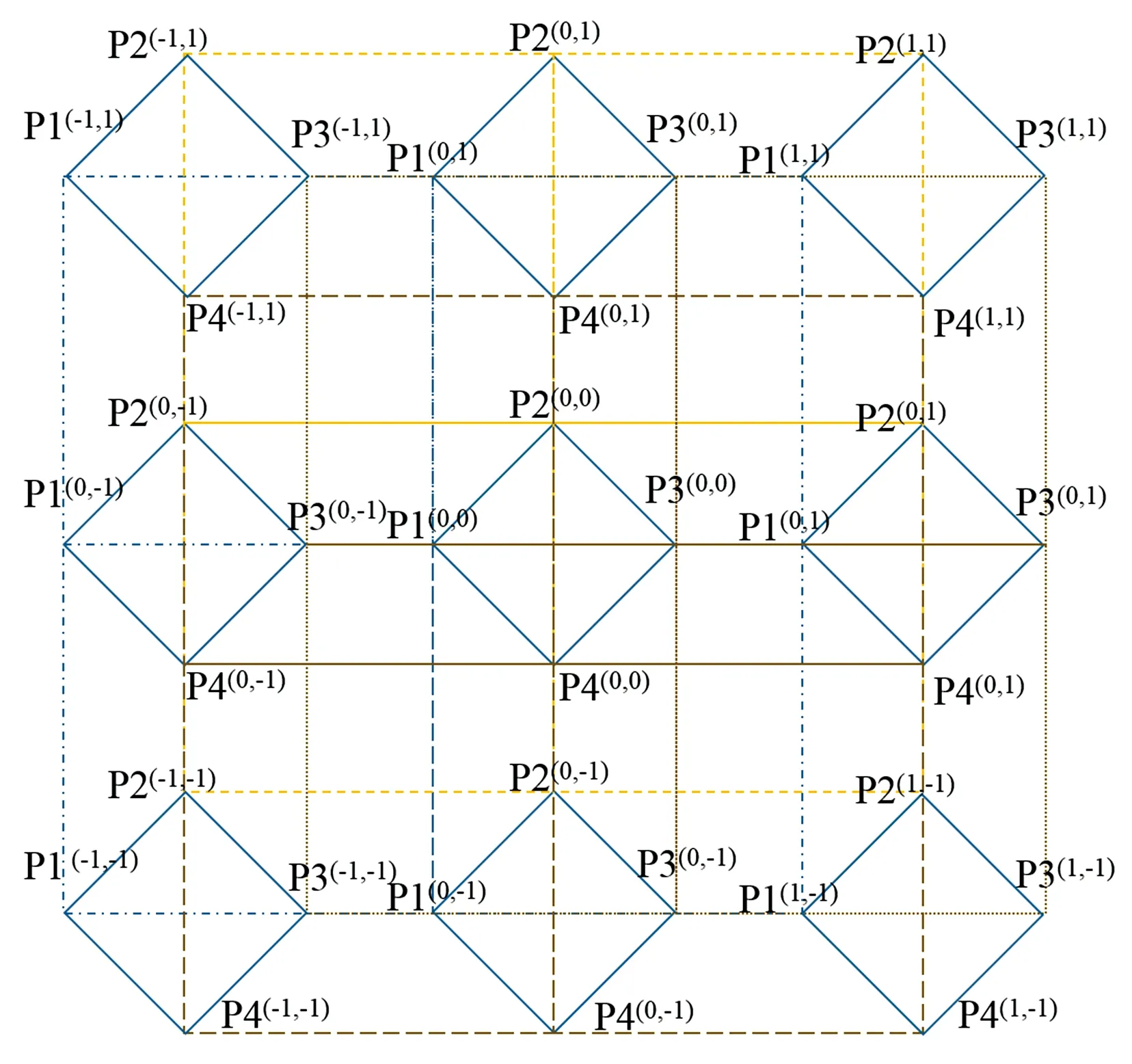
图9 并行标定示意图Fig.9 Schematic diagram of system matrix calibration in parallel

表1 并行标定算法Table 1 The system matrix calibration parallelly algorithm
2.3 试验结果分析
图10—图12列出多光谱数字物体“NSSC”和透射彩色物体“CS”的低分辨测量和并行压缩测量与成像光谱重建结果对比, 其中低分辨测量采用122×122, 为体现并行压缩感知优势采用更低分辨率61×61进行成像测量, 结果表明并行压缩感知计算层析成像光谱展现出更准确的光谱重建。
图10中(a)-NSSC/CS分别为探测器采集到的“NSSC”和“CS”物体的色散投影图像, 分辨率为122×122像素; (b)-NSSC/CS为使用DMD按照16×16分块并行压缩感知测量到的“NSSC”和“CS”物体图像, 相应的探测器成像分辨率为61×61, 采样率为0.687 5; (c)-NSSC/CS列为对压缩采样低分辨率图(b)-NSSC/CS重建得到的高分辨色散投影图, 分辨率为976×976。

图10 (a) NSSC/CS色散投影图像(122×122); (b) NSSC/CS压缩测量结果(61×61); (c) NSSC/CS重建色散投影图像(976×976)Fig.10 (a) NSSC/CS Low-resolution dispersion projection image in 122×122 pixels; (b) NSSC/CS Compressed sampling in 61×61 pixels; (c) NSSC/CS Reconstructed high-resolution dispersion projection image in 976×976 pixels
图11展示了数字物体“NSSC”光谱重建结果对比。 (a) 为122×122低分辨重建结果, 每个光谱图像都出现大量信号干扰: 在450, 470, 510和550 nm光谱图像中出现了不应出现的信号; 490 nm光谱物体“N”、 530 nm光谱物体“S”和570 nm光谱物体“S”较为准确重建, 但细节出现不同程度模糊, 仍不如BCSCTIS重建结果; 610 nm光谱图像则出现了比较严重的干扰。 (b) 为利用61×61像素的低分辨测量结果进行并行压缩感知光谱重建结果, 数字物体的每个字母在对应的波段均得到准确重建: 光谱物体“N”出现在490 nm、 左侧“S”出现在570 nm、 右侧“S”出现在530 nm、 “C”出现在610 nm, 和多光谱物体一致; (c) 为全波段成像结果, BCSCTIS重建彩色多光谱物体细节也更为清晰、 生动、 可辨。

图11 数字物体光谱重建结果, 波长单位为nm(a): 低分辨重建; (b): 并行压缩感知重建; (c): 全波段合成物体(上为低分辨重建合成, 下为压缩感知重建合成)Fig.11 Reconstructed spectral object of digital chart, nm as unit(a): Reconstructed multispectral image using conventional low-resolution dispersion; (b): Reconstructed multispectral image using BCSCTIS; (c): Multi-spectral composite colored image(the image by conventional low-resolution dispersion above, the image by BCSCTIS bellow)
图12展示了透射彩色物体“CS”光谱重建结果对比。 (a) 为122×122低分辨重建结果, 重建效果较差: 470和490 nm光谱中错误出现了“S”信号; 510, 530, 550和570 nm对应光谱呈现比较模糊的物体“C”, 同时还出现了信号“S”串扰,610 nm处出现强度高于630和650 nm光谱的“S”信号, 这也不符合红色滤光片的透过率曲线特征。 (b) 为61×61的低分辨并行压缩感知光谱重建结果: 绿色字母物体“C”信号明显出现在波长510, 530, 550和570 nm, 对应于图8中绿色滤光片58号光谱透过曲线范围, 红色字母物体“S”信号明显出现在波长630和650 nm, 对应于图10中红色滤光片25号光谱透过曲线范围, 其他波段没有出现干扰信号。 (c) 为全波段成像结果, BCSCTIS重建彩色物体细节也更为准确。

图12 数字物体光谱重建结果, 波长单位为nm(a): 低分辨重建; (b): 并行压缩感知重建; (c): 全波段合成物体(上为低分辨重建合成, 下为压缩感知重建合成)Fig.12 Reconstructed spectral transmitting colored object, nm as unit(a): Reconstructed multispectral image using conventional low-resolution dispersion; (b): Reconstructed multispectral image using BCSCTIS; (c): Multi-spectral composite colored image(the image by conventional low-resolution dispersion above, the image by BCSCTIS bellow
本节通过计算层析成像光学实验结合光谱色散投影并行压缩感知仿真实验验证了并行压缩感知计算层析成像光谱模型的正确性, 实验中BCSCTIS重建出更高分辨率的色散投影图像和更为准确的光谱立方体。 实验验证了依据压缩感知信号采样理论采用调制测量方式, 可以改善传统计算层析成像光谱系统中探测器分辨率对重建质量的制约问题。
3 结 论
从CTIS性能受FPA限制角度出发, 将压缩感知成像技术引入到CTIS的色散投影测量, 建立了并行压缩感知计算层析成像光谱系统, 可以实现超过探测器分辨率的光谱成像。 本文首先分析建立了BCSCTIS的成像模型, 然后通过仿真实验初步验证了方法的正确性, 接着又通过搭建实际CTIS光学系统, 完成了系统标定, 结合并行压缩测量仿真验证了BCSCTIS方法的优越性。 其中, 还提出并采用了系统并行逐点并行标定方法, 兼顾了标定精度和速率。 仿真实验使用高光谱数据集对传统CTIS方法和BCSCTIS进行了采样和数据重建质量对比, 实验结果表明了BCSCTIS方法和工作流程是可行的, 能显著提高光谱立方体重建质量。 光学实验使用DMD逐点和AOTF滤波器逐波长完成128×128×12三维空间图谱分辨率数据立方体到950×976二维投影分辨率系统投影矩阵的标定, 矩阵维度为927 200×196 608, 通过四个区域的并行标定方法, 光谱立方体标定时间降到了单点标定的四分之一。 实验中BCSCTIS方法分别在数字物体和彩色胶片物体实验上得到了验证, 可实现采用61×61的测量分辨率完成950×976分辨率投影图像获取, 进一步准确重建出128×128×12的三维空间图谱, 使得CTIS系统具有了当前探测器16×16倍高分辨率色散投影测量的能力, 最终改善光谱成像性能。 BCSCTIS重建质量、 性能受光谱分辨率和系统标定精确性影响, 在后续研究中, 一方面本课题将进一步研究集成光谱色散系统和并行采样系统的方法; 另一方面, 进一步研究更高分辨率的多光谱系统标定和系统标定矩阵精度的影响因素。

