钠冷快堆堆芯熔融物射流碎裂特性理论研究

葛 魁，张亚培，田文喜，苏光辉，秋穗正

(西安交通大学 核科学与技术学院，陕西 西安 710049)

钠冷快堆可显著提高铀资源利用率，而且在核废料处置方面具有重大改进[1-2]。我国的实验快堆已经临界，正处于示范快堆的研制阶段，需要掌握和积累大量的快堆技术和经验[3-8]。在无保护失流事故(ULOF)、无保护失热阱事故(ULOHS)和无保护反应性引入事故(UTOP)中，若液态金属钠发生沸腾现象，进一步加剧事故后果，可能导致堆芯损坏和熔化[9-13]。堆芯熔融物可能掉入冷却剂中并与液态金属钠相互作用(MFCI)，导致熔融物的碎裂及凝固，并在堆芯捕集器或下封头内重定位形成堆芯碎片床[14]。熔融物的射流碎裂特性直接关乎堆芯碎片床的冷却及再临界行为。自20世纪钠冷快堆问世以来，其严重事故下堆芯熔融物射流碎裂特性备受关注，亦成为研究的重点和难点。

欧盟联合研究中心JRC基于BETULLA实验装置[15-16]开展了熔融UO2、Cu和不锈钢与液态金属钠相互作用实验研究，在钠池的不同位置处布置有热电偶，以测量MFCI过程中的温度响应。此外，研究人员还获得了碎片的尺寸分布规律，并对典型碎片样品的金相特征进行了分析。西安交通大学[17-19]搭建了钠冷快堆堆芯熔融物碎裂特性研究实验台架COSA以开展熔融物过热度、熔融物射流直径和钠池初始过冷度等参数对碎裂特性的影响研究。堆芯熔融物选择铝、不锈钢和铜作为堆芯替代材料，冷却剂选用液态金属钠。熔融堆芯替代材料过热度可达200 ℃以上，熔融物射流直径16～30 mm；液态金属钠池温度可达450 ℃，液态金属钠装量35 kg，钠池深度0.5 m。根据实验结果获得了MFCI过程中能量释放特性、熔融物碎片形态特征和尺寸分布规律。

基于熔融物与冷却剂之间为液-液或液-气接触的假设，Donne等[20]对过热液态金属钠中气泡的增长特性进行了研究，根据简化的质量和动量方程，推导球形交界面的加速度方程；推广至液-液系统后，根据球形交界面的加速度方程，Plesset等[21-22]基于小幅度分析法在液-液系统中球形交界面处建立了扰动增长方程，并推导出界面稳定性判定的准则；周源[23]基于小幅度分析法，推导出熔融物液滴与冷却剂交界面上的扰动增长方程，拟合获得了半经验关系式。此外，比较经典的熔融物液滴热碎裂模型包括Ciccarelli和Frost[24]热碎裂模型、Kim和Corradini[25]热碎裂模型等，前者是基于液膜坍塌后冷却剂再汽化形成的高压区挤压熔融物形成细丝的机理，而后者是基于液膜坍塌后冷却剂以液柱形式冲入熔融物内部后汽化形成的高压区导致熔融物碎裂的机理。但上述模型中，均未将冷却剂核态沸腾效应和熔融物凝固效应考虑在内。

因此，本文基于线性稳定性理论、运动学方程和交界面修正拉普拉斯定律，推导出考虑沸腾和凝固效应的熔融物射流表面不稳定性增长方程，建立液态金属钠中熔融物射流碎裂模型，提出典型环境中熔融物射流碎裂准则，并使用熔融物射流碎裂模型对COSA实验结果进行对比分析。

1 熔融物射流碎裂模型开发

熔融物射流与液态金属钠交界面因受力不平衡而出现界面扰动，基于K-H不稳定性分析方法[26-27]，在充分考虑沸腾和凝固双重效应条件下，可利用线性稳定性理论和流体力学基本守恒方程分析界面扰动增长规律。

在模型开发过程中，参考已有相关文献[26-27]进行了一定的基本假设，以简化物理模型：1) 熔融物射流与液态金属钠均为连续介质、不可压缩流体且不混溶，不考虑流体的黏性，且熔融物射流与液态金属钠的物性参数不随温度而变；2) 在圆柱坐标系下，仅考虑两种流体的轴向主流速度和径向扰动速度，且主流速度与重力加速度方向平行，故两种流体为无旋流动，假设为势流；3) 在应用线性稳定性理论时，假设界面扰动振幅远小于熔融物射流直径；4) 采用固体硬壳抗弯曲理论方程时，交界面处固体硬壳的厚度足够小，且不考虑边界固体硬壳边界问题；5) 固体硬壳的惯性力忽略不计，且不考虑硬壳内部的温度梯度和所产生的热应力；6) 钠沸腾过程产生的冲击压力与界面扰动振幅呈线性函数关系；7) 采用λm/2(λm为最不稳定波长)作为熔融金属铝射流碎裂的质量中值直径(DMM)预测值。

1.1 控制方程

在圆柱坐标系下，两相交界面附近处的连续流体仅考虑轴向和径向维度，可得简化的基本控制方程[28]，其中熔融物和冷却剂(液态金属钠)的相关物理量分别采用角标m和f进行区别。

界面扰动的连续性方程为：

(1)

式中：r为径向距离，m；ur为界面扰动径向速度，m/s；uz为界面扰动轴向速度，m/s；z为轴向距离，m。

界面扰动的动量方程为：

(2)

(3)

式中：t为时间，s；Uz为流体轴向的主流速度，m/s；fr为单位质量流体所受的径向质量力之和，m/s2；ρ为流体密度，kg/m3；p为压力，Pa；fz为单位质量流体所受的轴向质量力之和，m/s2。

主流速度与重力加速度方向平行，故两种流体为无旋流动。交界面扰动的速度势函数由φ表示，并且满足以下方程：

(4)

因此式(1)可转化为：

(5)

熔融物射流和液态金属钠中远离交界面处的速度势函数满足以下边界条件：

(6)

式中，φm和φf分别为熔融物射流和液态金属钠的速度势函数。

图1为交界面示意图，在考虑沸腾和凝固效应后，根据交界面动力学边界条件[29]，可推导出受力平衡时修正的拉普拉斯方程：

图1 交界面示意图Fig.1 Schematic diagram of interface

(7)

(8)

式中：E为杨氏模量，Pa；δ为固体硬壳厚度，m；γ为泊松比。

1.2 界面扰动增长规律

当熔融物射流与液态金属钠之间的交界面受力不平衡时，界面扰动振幅可表示为：

(9)

式中：a0为系数；w为角频率；k为界面扰动波数。

熔融物射流与液态金属钠的速度势函数分别为：

φm(t,r,z)=φ0(ekr-e-kr)ei(wt-kz)

(10)

φf(t,r,z)=φ′0e-krei(wt-kz)

(11)

则界面扰动的径向速度可分别由速度势函数和界面扰动振幅计算，即：

(12)

故：

(13)

(14)

由式(9)～(14)推导可得：

(15)

(16)

式中，Um和Uf分别为熔融物和冷却剂的界面扰动轴向速度，m/s。

单位质量流体所受的径向质量力fr取值为零，界面扰动在径向上发展并在周向上传播，在r方向上对式(2)进行积分，并将式(4)中界面扰动的径向速度代入其中，推导得到：

(17)

将式(17)分别应用于熔融物射流和液态金属钠，可得：

(18)

(19)

式中：ps为压力常量，Pa；p0为熔融物射流的压力常量，Pa；p′0为液态金属钠的压力常量，Pa；p为压力，Pa。

如式(18)、(19)所示，涉及熔融物射流和液态金属钠的速度势函数是关于时间t和轴向z的偏导数，其根据式(10)、(11)可推导获得：

(20)

(21)

(22)

(23)

因此，将式(20)、(21)和式(22)、(23)分别代入式(18)和式(19)后，进一步推导可得熔融物射流和液态金属钠中的压力pm和pf，如下所示：

pm=iρmφ0(w-k(Uz)m)·

(ekr-e-kr)ei(wt-kz)+p0(t,z)

(24)

pf=iρfφ′0(w-k(Uz)f)e-krei(wt-kz)+p′0(t,z)

(25)

将式(24)、(25)代入式(7)中，可得：

iρmφ0(w-k(Uz)m)(ekr-e-kr)ei(wt-kz)-

iρfφ′0(w-k(Uz)f)e-krei(wt-kz)+

(p0(t,z)-p′0(t,z))

(26)

当熔融物射流与液态金属钠之间的交界面处于未受扰动状态时，液态金属钠核态沸腾或过渡沸腾过程中出现了气泡坍塌或脱离现象，液态金属钠以液柱形式冲击交界面，该冲击压力由势能转换而来，可等效为：

(27)

将式(27)代入式(26)后，可得：

iρmφ0(w-k(Uz)m)(ekr-e-kr)ei(wt-kz)-

iρfφ′0(w-k(Uz)f)e-krei(wt-kz)+pw(t,z)

(28)

式中，pw为冲击压力，Pa。

液态金属钠液柱对交界面的冲击压力pw(t，z)源于液态金属钠沸腾过程中气泡坍塌或脱离后的势能转换，假设该冲击压力与界面扰动振幅a0ei(wt-kz)呈线性函数关系：

pw(t,z)=Cpba0ei(wt-kz)

(29)

式中，Cpb为冲击压力系数，Pa/m。

将式(9)、式(15)、(16)和式(29)代入式(28)中，消除未知量φ0和φ′0，进一步简化处理可得：

(30)

将式(30)整理为关于角频率w的函数，即：

(ρ′m+ρf)w2-2k(ρ′m(Uz)m+ρf(Uz)f)w-

(31)

根据一元二次方程的求根公式，式(31)中w的解为：

(32)

(33)

(34)

界面扰动增长率分为时间增长率φt和沿轴向的空间增长率φz，定义为：

(35)

(36)

采用界面扰动波长作为熔融物射流碎裂的特征尺寸时，可忽略沿轴向的空间增长率φz：

φz=Re(ik)=0

(37)

根据式(32)和式(35)可得界面扰动的时间增长率φt：

(38)

(39)

(40)

根据式(40)计算界面扰动的时间增长率，等号右边第1项表示界面两侧流体因相对运动产生动态压降而导致的失稳效应，第2项表示液态金属钠在沸腾过程中气泡坍塌或脱离时液柱对交界面形成冲击压力而导致的失稳效应，第3项表示熔融物射流与固体硬壳之间的界面张力和液态金属钠与固体硬壳之间的界面张力对交界面的稳定效应，第4项表示固体硬壳的抗弯曲强度对交界面的稳定效应。

2 界面不稳定性分析

当熔融物射流与液态金属钠之间交界面的失稳效应强于稳定效应时，诱发界面不稳定性，即界面扰动的时间增长率φt>0，推导得到：

(41)

故存在某个临界波长λcr，当λ>λcr时，式(41)成立。

本文考虑了3种不同的碎裂情形：1) 液态金属钠未沸腾且熔融物未凝固(下标为h)；2) 液态金属钠未沸腾而熔融物发生凝固(下标为s)；3) 液态金属钠发生沸腾且熔融物凝固(下标为bs)。

当液态金属钠未沸腾且熔融物未凝固，即Cpb=0 Pa/m和Ds=0 N·m，该种情况下熔融物射流碎裂准则为：

(42)

(43)

式中，λh-cr为液态金属钠未沸腾且熔融物未凝固情况下的临界波长。

该临界波长λh-cr作为特征尺寸时，计算得到临界韦伯数Wecr，若We>Wecr，则认为熔融物射流会发生碎裂行为，反之不然。

(44)

(45)

当液态金属钠未沸腾，即Cpb=0 Pa·m-1，而熔融物发生凝固，该种情况下熔融物射流碎裂准则为：

(46)

式中，λs-cr为液态金属钠未沸腾且熔融物凝固情况下的临界波长。

(47)

式中，λs′-cr为考虑熔融物射流的凝固行为对两相交界面的稳定效应远强于界面张力作用简化下的λs-cr。

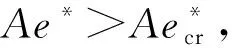
(48)

(49)

(50)

当液态金属钠发生沸腾且熔融物凝固，根据式(41)所得的临界波长λbs-cr极为复杂，若液态金属钠沸腾现象导致的界面失稳效应远大于流体因相对运动产生动态压降而导致的失稳效应时，该种情况下熔融物射流碎裂准则为：

λ>λbs-cr=

(51)

式中，λbs-cr为液态金属钠沸腾且熔融物凝固情况下的临界波长。

(52)

式中，λbs′-cr为考虑熔融物射流的凝固行为对两相交界面的稳定效应远强于界面张力作用简化下的λbs-cr。

从式(52)可看出，临界波长λbs′-cr与固体硬壳的抗弯曲应力Ds和液态金属钠沸腾产生的冲击压力系数Cpb相关，本文采用修正气动弹性系数Ae*和修正欧拉数Eu*描述熔融物射流碎裂行为，其中Eu*表征压力与惯性力的比值。采用λbs′-cr作为特征尺寸时，当(Ae*·Eu*)>(Ae*·Eu*)cr，熔融物射流发生碎裂，反之不然。

(53)

(54)

(Ae*·Eu*)>(Ae*·Eu*)cr=

(55)

式中，Δp为压力，Pa。

3 最不稳定波长

熔融物射流与液态金属钠的相互作用是一个多物理场耦合的瞬态过程，会产生各种尺寸的熔融物碎片，小于某一尺寸的熔融物碎片质量占总质量的50%时，将该尺寸定义为熔融物碎片的DMM，作为一种统计平均值，用于分析评估熔融物射流的碎裂程度。

(56)

将式(56)简化后，可得λm的一元四次方程：

(57)

根据一元四次方程的求根公式，其中正实根为最不稳定波长λm，即：

(58)

(59)

(60)

(61)

D1=9(σm+σf)2-60DsCpb

(62)

1 080DsCpb(σm+σf)

(63)

当液态金属钠未沸腾且熔融物未凝固，即Cpb=0 Pa/m和Ds=0 N·m，最终可得最不稳定波长λm为：

(64)

当液态金属钠未沸腾，即Cpb=0 Pa/m，而熔融物发生凝固，最不稳定波长λm为：

(65)

当液态金属钠发生沸腾且熔融物凝固，若液态金属钠沸腾现象导致的界面失稳效应远大于流体因相对运动产生动态压降而导致的失稳效应时，最不稳定波长λm为：

(66)

若熔融物射流的凝固行为对两相交界面的稳定效应远强于界面张力作用，最不稳定波长λm为：

(67)

(68)

D3=-60DsCpb

(69)

(70)

若液态金属钠的沸腾现象和熔融物射流的凝固行为影响显著，可以忽略界面张力和流体间的相对运动，最不稳定波长λm为：

(71)

4 模型预测与实验结果对比

本文开发的模型考虑了3种因素的影响：流体间相对速度、钠沸腾现象和熔融物凝固。其中流体间相对速度通过经典的K-H不稳定性体现，采用了冲击压力系数Cpb和抗弯曲强度Ds分别体现钠沸腾现象和熔融物凝固过程对射流碎裂行为的影响。Cpb和Ds是随熔融物射流和液态金属钠的温度、传热系数等热力学参数变化的物理量。

本文首先分析Cpb和Ds对φt、λcr和λm的影响，然后基于不同Cpb和Ds分别预测了非沸腾条件下和沸腾条件下熔融物射流碎裂的质量中值直径，并与COSA实验结果[17-19]进行对比分析。

4.1 非沸腾条件下熔融金属铝射流碎裂行为

以COSA实验中非沸腾条件下熔融金属铝射流碎裂特性实验工况为分析对象，工况参数列于表1。液态金属钠为静止状态，流体间相对速度|(Uz)m-(Uz)f|等效为射流速度。此外，液态金属钠未发生沸腾现象，熔融金属铝射流的碎裂行为同时受到流体间相对运动、界面张力和凝固效应的影响，即Cpb=0 Pa/m且Ds≠0 N·m，通过改变Ds分析其对熔融金属铝射流碎裂特性的影响。

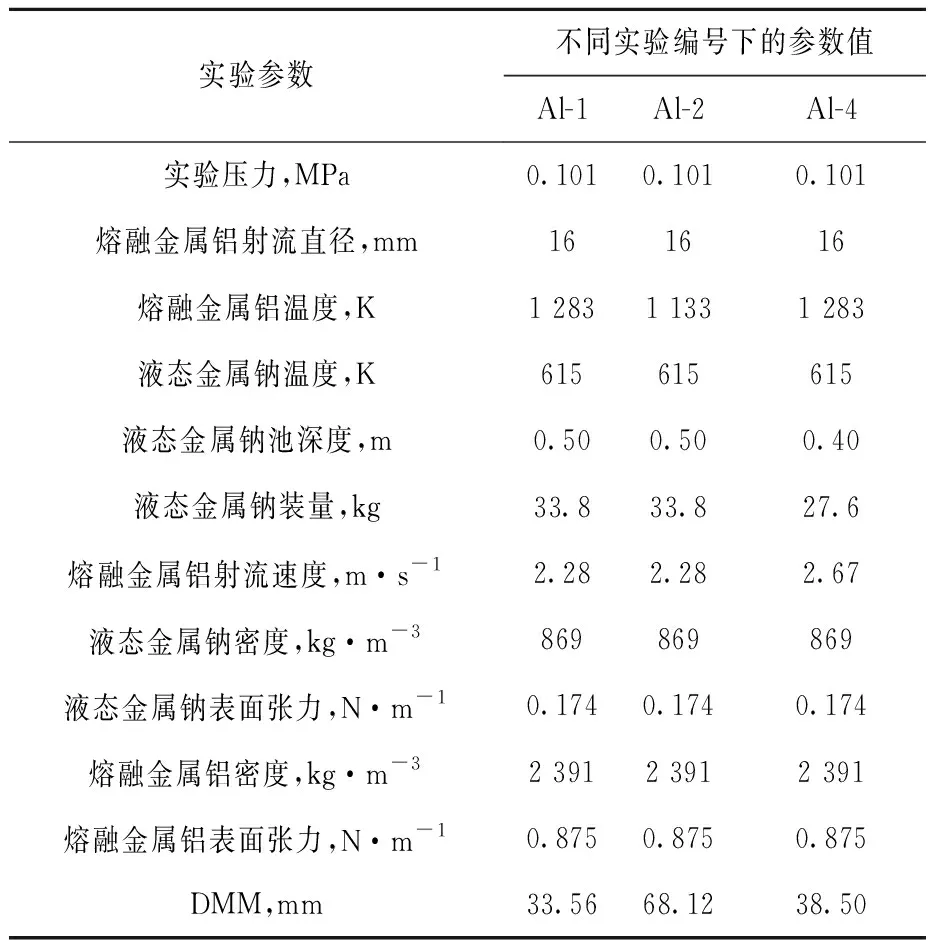
表1 熔融金属铝实验参数Table 1 Experimental parameter with molten material as Al

如图2所示，当流体间相对速度相同时，随着Ds的增大，φt曲线发生明显变化，λcr和λm均随之增大，但φt的峰值显著减小，说明交界面处熔融金属铝射流的凝固行为对界面扰动的稳定效应逐渐增强，更有助于界面稳定性。此外，当Ds相同时，流体间相对速度越大，λcr和λm反而越小，φt的峰值明显提高，说明流体间相对运动所导致的界面失稳效应逐渐增加，更易导致界面不稳定性。

流体间相对速度：a——2.28 m·s-1；b——2.67 m·s-1图2 非沸腾条件下界面扰动增长率的变化Fig.2 Change of growth rate of interfacial disturbance in non-boiling condition

非沸腾条件下λcr和λm的变化如图3所示，λcr和λm均随着Ds的增大而增大，随着流体间相对速度的增大而减小。由图3可见，λcr和λm间的差距逐渐增大，交界面出现扰动至发生碎裂行为所需时长增加，且两者相对Ds的变化率逐渐减小。

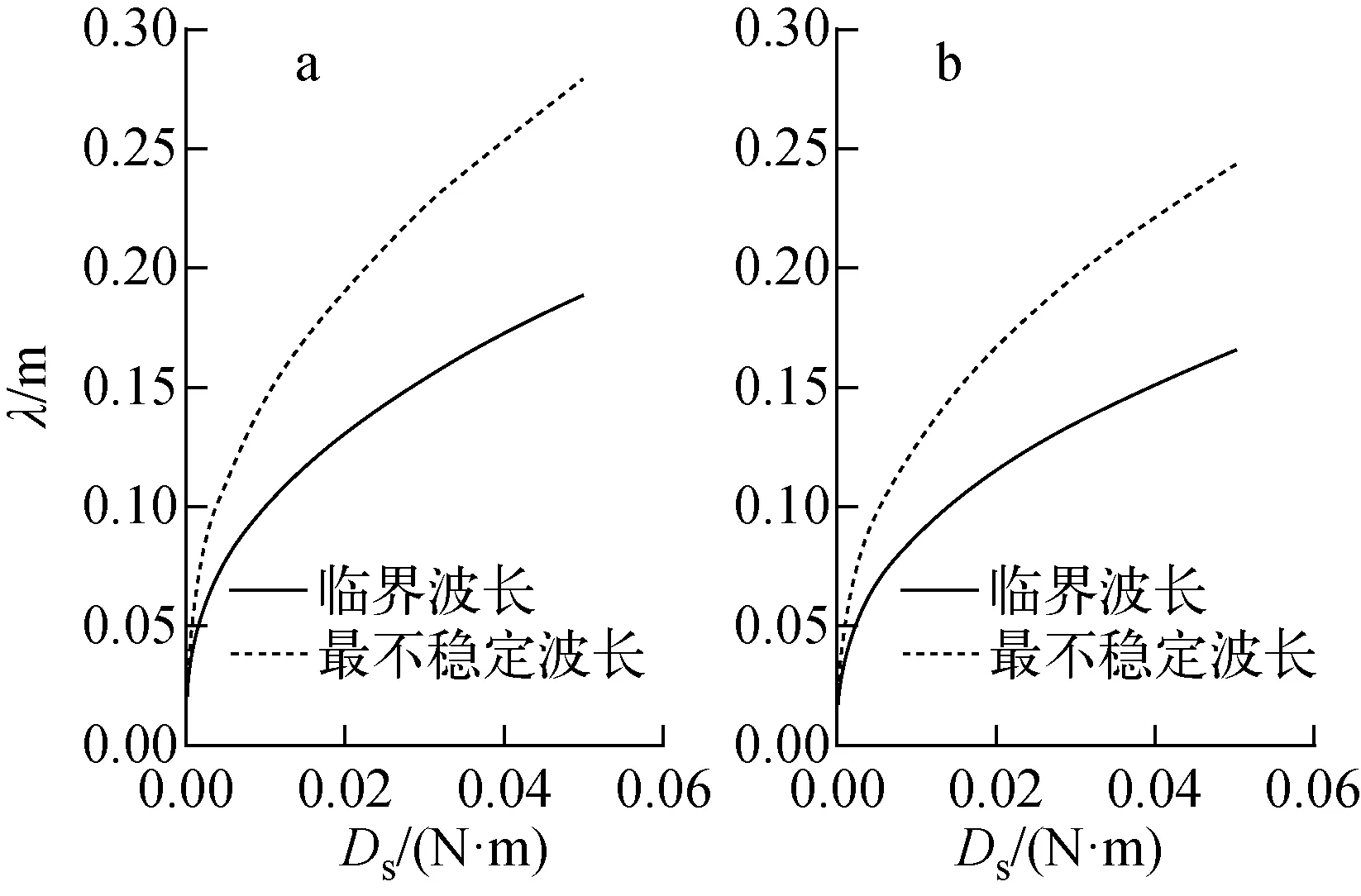
流体间相对速度：a——2.28 m·s-1；b——2.67 m·s-1图3 非沸腾条件下λcr和λm的变化Fig.3 Change of λcr and λm in non-boiling condition

图4 非沸腾条件下DMM对比Fig.4 Comparison of DMM in non-boiling condition

4.2 沸腾条件下熔融不锈钢射流碎裂行为

不锈钢是钠冷快堆核燃料包壳的主要材质，以COSA实验中熔融不锈钢射流碎裂特性实验工况为分析对象(工况参数列于表2)开展液态金属钠的沸腾行为(Cpb≠0 Pa/m)和熔融不锈钢的凝固效应(Ds≠0 N·m)对其的影响研究。

表2 熔融金属不锈钢实验参数Table 2 Experimental parameterwith molten materials as stainless steel

针对流体间相对速度为2.28 m·s-1和2.67 m·s-1，图5示出不同Ds和Cpb下界面扰动增长率的变化。Ds越大，熔融物表面的硬壳抑制扰动增长的能力越强。而Cpb越大，钠沸腾现象促进扰动增长的能力越强。当相对速度相同时，随着Ds的减小和Cpb的增大，界面不稳定性更易诱发，λcr和λm均随之减小，φt的峰值相应提高。如图5所示，当Cpb由106Pa·m-1增加至107Pa·m-1时，φt变化出现显著提高，增长幅度远大于Cpb由0 Pa·m-1增加至106Pa·m-1时，亦说明液态金属钠沸腾效应对界面扰动的促进作用显著增强；当Ds由10-7N·m增加至10-6N·m时，φt变化出现一定程度降低，其减小幅度略小于Ds由10-6N·m增加至10-5N·m时，亦说明熔融不锈钢的凝固行为对界面扰动的稳定效应逐渐提高。当流体间相对速度从2.28 m·s-1增加至2.67 m·s-1时，在相同Cpb和Ds条件下φt的峰值均提高，而λcr和λm均随之降低，但降低幅度随Cpb的增大而减小，源于流体间相对运动对界面失稳效应的贡献比例逐渐降低。

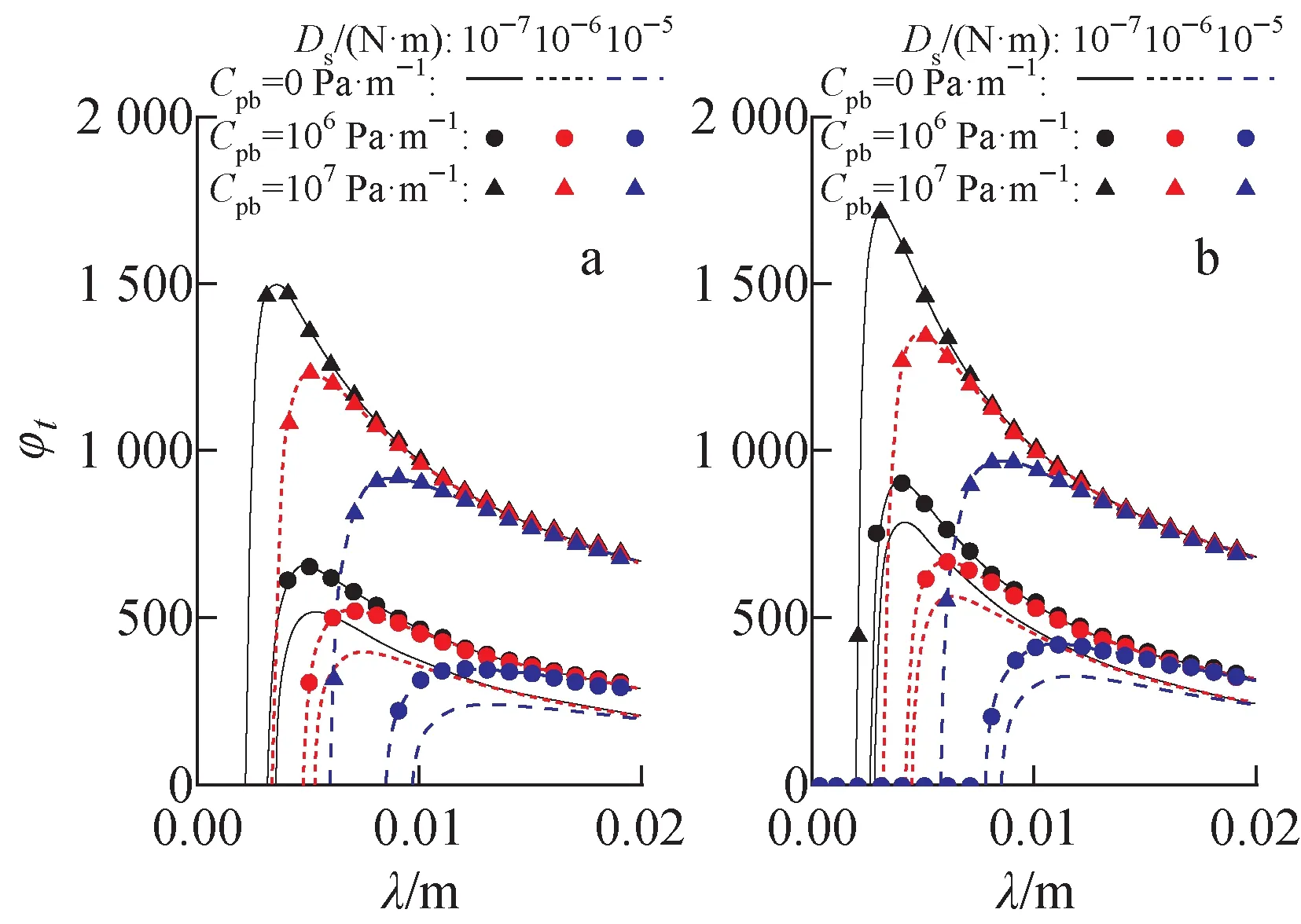
流体间相对速度：a——2.28 m·s-1；b——2.67 m·s-1图5 沸腾条件下界面扰动增长率的变化Fig.5 Change of growth rate of interfacial disturbance in boiling condition

图6示出沸腾条件下λm的变化。如图6所示，随着Cpb在105～109Pa·m-1范围内逐渐增大，λm首先缓慢减小，然后快速减小，最后再缓慢减小。这是因为钠沸腾现象和流体间速度差都是引起界面扰动的重要因素，而液态金属钠沸腾行为对界面失稳效应的贡献比例随着Cpb的增大而增强，从弱于、到强于、再到远强于流体间相对运动所导致的界面失稳效应。在高Ds条件下，Cpb增大导致λm降低的速率提高，但其值始终高于低Ds条件下的λm。此外，在低Cpb条件下(如105Pa·m-1)，流体间相对运动和液态金属钠沸腾行为所导致的界面失稳效应均不可忽略，均有利于界面扰动的发生和增长，故所得的最不稳定波长λm随流体间相对速度的增大而减小；而在高Cpb条件下，液态金属钠沸腾成为界面失稳的主导因素，流体间相对运动对界面扰动的贡献比例逐渐降低，故流体间相对速度对λm的影响较小。

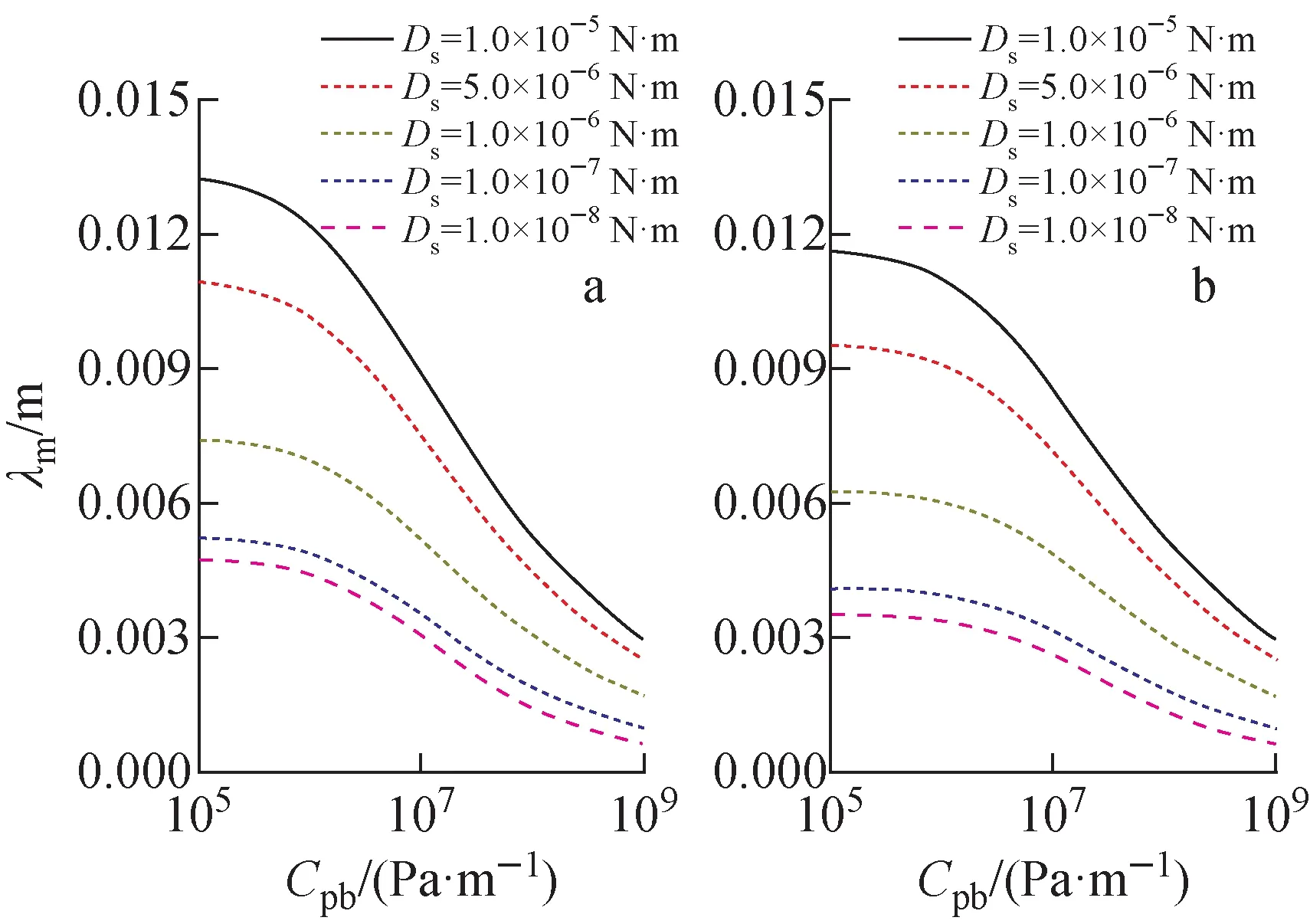
流体间相对速度：a——2.28 m·s-1；b——2.67 m·s-1图6 沸腾条件下λm的变化Fig.6 Change of λm in boiling condition

在λm计算公式(式(58)～(63))中，Ds和Cpb是影响其计算结果的敏感性参数，两者均与熔融物和液态金属钠初始温度、传热系数、热扩散率等热力学参数相关，且具有负相关性。根据图6中λm与Cpb的关系曲线，当Cpb小于106Pa·m-1时，λm受Cpb的影响较小，归因于流体间相对运动对界面失稳的贡献较大，而当Cpb大于108Pa·m-1时，λm随Cpb变化速率降低，归因于流体间相对运动对界面失稳的贡献可忽略不计。

而实验中获得的不锈钢大多呈薄片状和球壳状形态，或带有凹穴或孔洞分支，表明实验过程中出现明显的液态金属钠沸腾现象，沸腾过程中气泡的增长和坍塌导致了硬壳碎裂(薄片状和球壳状形态)以及液态金属钠渗入熔融不锈钢内部(带有凹穴或孔洞分支)。同时相对速度为2.28 m·s-1和2.67 m·s-1的两个实验的DMM有较明显的差异，证明不可忽略流体间相对运动的影响。根据实验结果分析，液态金属钠沸腾效应(Cpb)为熔融不锈钢射流碎裂的主要因素，但流体间相对运动所导致的界面失稳效应同样不可忽略，因此认为Cpb可能在106～108Pa·m-1范围内。

针对Ds分别为10-6N·m和10-5N·m，在不同Cpb条件下模型预测值与流体间相对速度之间的关系如图7所示，也说明Cpb在106～108Pa·m-1范围内取值的合理性。随着Cpb的增大，流体间相对速度对模型预测值的影响减小，关系曲线下移且斜率降低，然而随着Ds的增大，对界面稳定效应增强，关系曲线上移且斜率稍微增大。从图7中可看出，当Cpb在106～108Pa·m-1范围内取值时，若Ds减小至10-6N·m以下，图7a中曲线下移，则对SS-1实验的预测差距增大，若Ds增大至10-5N·m以上，图7b中曲线上移，亦增大了对SS-2实验的预测差距。因此，当Cpb在106～108Pa·m-1范围内，则Ds在10-5～10-6N·m范围内，模型预测与实验测量的DMM符合较好。

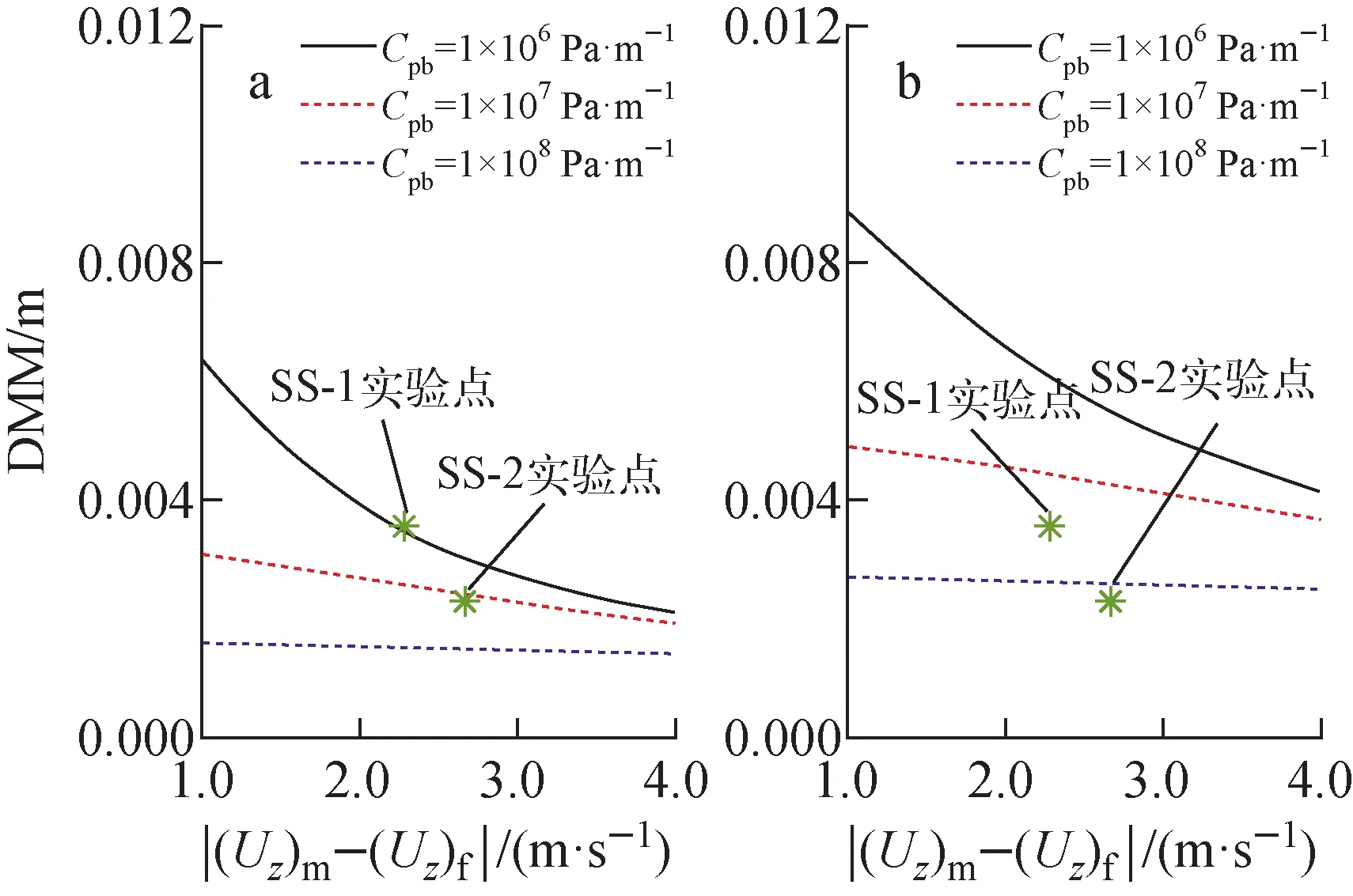
a——Ds=10-6 N·m；b——Ds=10-5 N·m图7 沸腾条件下DMM对比Fig.7 Comparison of DMM in boiling condition

非沸腾工况及沸腾工况均受到Ds的影响。Ds越大，熔融物表面的硬壳抑制扰动增长的能力越强，因此随着Ds增大，临界波长和最不稳定波长均随之增大。在非沸腾工况下，熔融物温度较低，硬壳较厚，因此Ds较大(在2.0×10-3～1.0×10-2N·m范围与实验结果符合较好)。而对于沸腾工况，在10-5～10-6N·m范围内与实验结果符合较好。

5 结论

本文基于K-H不稳定性分析方法，充分考虑沸腾和凝固双重效应，利用线性稳定性理论，通过运动学方程和交界面拉普拉斯定律推导获得界面扰动增长规律方程，提出典型环境中熔融物射流碎裂准则，建立液态金属钠中熔融物射流碎裂模型，通过与实验结果对比分析，研究熔融物射流凝固行为和液态金属钠沸腾行为对其碎裂特性的影响，所得主要结论如下。

1) 本文提出了典型环境中熔融物射流碎裂准则：若沸腾和凝固均未发生，熔融物射流碎裂准则为We>2π；若沸腾未发生，而凝固发生，忽略界面张力后，熔融物射流碎裂准则为Ae*>(2π)3；若沸腾和凝固同时发生，忽略界面张力和流体间相对运动后，熔融物射流碎裂准则为(Ae*·Eu*)>(2π)4。

2) 采用带凝固项的碎裂模型分析非沸腾条件下熔融金属铝射流碎裂实验，3组实验中凝固效应不同，当Ds在2.0×10-3N·m附近时，模型预测值与Al-1、Al-4实验点符合较好，而Al-2实验结果与Ds在1.0×10-2N·m的模型预测值更接近。

3) 针对沸腾条件下熔融不锈钢射流碎裂实验，液态金属钠沸腾效应为主要因素，且流体间相对运动所导致的界面失稳效应不可忽略，根据λm与Cpb的关系和DMM与流体间相对速度的关系，认为Cpb在106～108Pa·m-1范围内，且当Ds在10-5～10-6N·m范围内时，模型预测值与实验测量的DMM符合较好。

由于液态金属钠为非透明介质，难以获得射流碎裂的可视化结果，如碎裂过程的硬壳厚度(可用于计算抗弯曲强度)和界面扰动振幅(可用于计算冲击压力系数)等，因此仅分析实验数据很难对理论模型进行进一步改进。近期有些学者利用粒子法(如MPS)对射流碎裂过程进行了模拟研究[30-31]，后续可通过数值模拟方法获得碎裂过程的关键参数，对模型进行详细修正及改进。

同时，本文的理论模型是基于线性稳定性理论及一些基本假设所提出，两相交界面均为规则结构。后续有必要针对复杂环境下非线性变形的交界面不稳定性进行研究，分析研究不同条件下熔融物射流碎裂特性。