超单元技术在内置换料水箱过滤器抗震分析中的应用

兰天宝，彭星铭，黄若琳，王艳苹

(中国核电工程有限公司，北京 100840)

在核电设备抗震分析中，设备往往需要经过多次迭代优化才能满足规范设计要求。设备设计中会涉及大量有限元分析计算，对于一些大模型(百万单元量级、千万自由度量级)，计算会比较耗时，从而影响设计进度，因此需要找到一种适用于初步设计的快速分析方法。在华龙二号内置换料水箱过滤器系统过滤模块初步设计过程中遇到了求解耗时和需求时效的矛盾问题，需要在保证结果精度的前提下快速评估设备并给出输出数据。随着超单元方法的应用日渐成熟，在初步设计阶段可以采用超单元方法进行结构优化设计，用于解决求解的时效问题，提高设计效率。

1 过滤器结构介绍

核电厂安全壳内发生冷却剂丧失事故(loss of coolant accident,LOCA)或主蒸汽管道断裂等事故时，事故载荷将对周围的保温材料、土建结构及其他物质等形成冲击破坏，从而导致大量各类碎渣的产生。如果碎渣传递至喷淋系统入口处的水池(例如二代加压水堆机组中的地坑，三代压水堆机组中内置换料水箱)并沉积在其内部，碎渣累积将会导致喷淋系统流量不足，影响核电厂安全。

在事故工况下，需要对内置换料水箱(或地坑)中的碎渣进行过滤。安全壳内置换料水箱过滤器系统布置在水箱上层楼板，起到过滤碎渣的功能。系统中核心装备包含多组过滤器模块，如图1所示，每组过滤器模块主要包括以下部件：2个滤网鳍片组，提供大面积的滤网；1个流道框架，作为整个部件的支撑框架，同时其内部空间组成了过滤器的汇流流道；2个支撑梁组件，用于加强滤网鳍片组的支撑；多个压板，用于滤网鳍片组与流道框架的固定；若干支脚中间板，用于固定框架与埋件。

图1 过滤器结构示意

由于过滤系统的正常运行十分重要，因此需要确保在事故工况下过滤器能够满足过滤功能。为了确保设备的完整性和功能性，需要对过滤器进行事故工况下的分析计算，如抗震分析等。

2 超单元方法介绍

虽然随着技术的发展，计算机的性能已不断提高，但是有限元模型的规模(单元数量、接触数量)也不断变大，自由度数量变多，意味着用有限元分析解决问题可能仍需要数小时的计算时间。目前很多有限元商业软件(如Nastran、ANSYS等)使用稀疏方程有效地解决了大型方程组求解慢的问题。然而，超单元方法提供了更高的效率，在解决非常大的、复杂的有限元模型时发挥了关键作用。将较大的结构分解为较小的子结构等价集合，称为超单元方法，该方法基于瑞利里兹法[1]。超单元方法在大型全系统分析中特别有效，非常适合用于飞机、车辆或船舶等复杂装备行业。目前，有关超单元方法的应用及研究已十分成熟，被应用到多个行业：有实践将超单元方法应用到飞机设计中[2-3]，有将该方法应用到核电厂贮存格架的抗震非线性计算中[4]，有实践将该方法应用到汽车车身的模态计算[5]，也有对该方法关键原理和技术的研究[6-8]。

超单元方法具有以下优点：

1)节省时间成本。

设计者很少遇到只需要进行一次有限元计算便可解决问题的情形，往往需要尝试多次重复的计算来解决问题，重复的计算会耗费大量时间，如果采用超单元方法则可以节省求解时间。

2)便于处理大模型。

当处理大的计算模型(单元数量多、接触数量多)时对硬件性能要求便会提高，即要求较大的内存和硬盘空间。当硬件无法满足有限元计算需求时，可采用超单元方法将大模型分为几个组合的超单元小模型，通过减少每个超单元小模型的自由度从而满足硬件计算要求。

3)可选择部分输出。

当模型较大时，有限元分析软件输出的数据规模也会很大，而超单元方法可以实现对每个超单元的选择性输出，从而节省时间和空间，方便查看结果。

超单元方法应用在模态求解中也称为模态综合法，即将原始模型分为若干子结构，对各个子结构进行模态分析，然后进行结果组合，获得完整模型的动态特性参数，系统的动态特性方程如下：

(1)

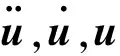
(2)

式中：角标m表示子结构单元自由度，发生在划分结构的界面节点处；角标c表示其余自由度。

3 分析模型

3.1 传统方法有限元模型

传统计算方法(以下简称传统方法)采用壳单元对过滤器框架、支撑条、滤网等部件进行建模，过滤器中的螺栓连接通过约束方程实现，大量螺栓用质量单元简化等效，优化后的过滤器有限元模型如图2所示。

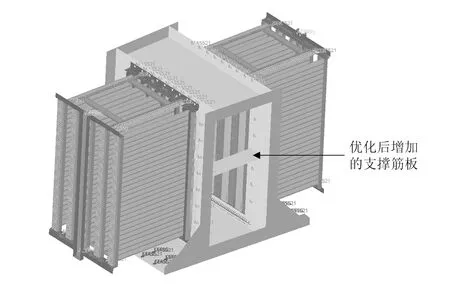
图2 过滤器有限元模型

3.2 超单元模型

为了节省计算时间，一般选取重复或结构复杂的部件作为超单元。由于过滤器的滤网结构复杂，其单元数量比框架多，而且过滤器的滤网与框架的螺栓连接处可作为边界控制点，因此选择滤网作为超单元结构。为了满足过滤压降等一些技术要求，滤网在本次设计中已固化，因此只对框架结构进行分析、优化，以满足设备对刚度的要求，超单元模型如图3所示，此时的滤网相当于由质量矩阵和刚度矩阵组成的单元。

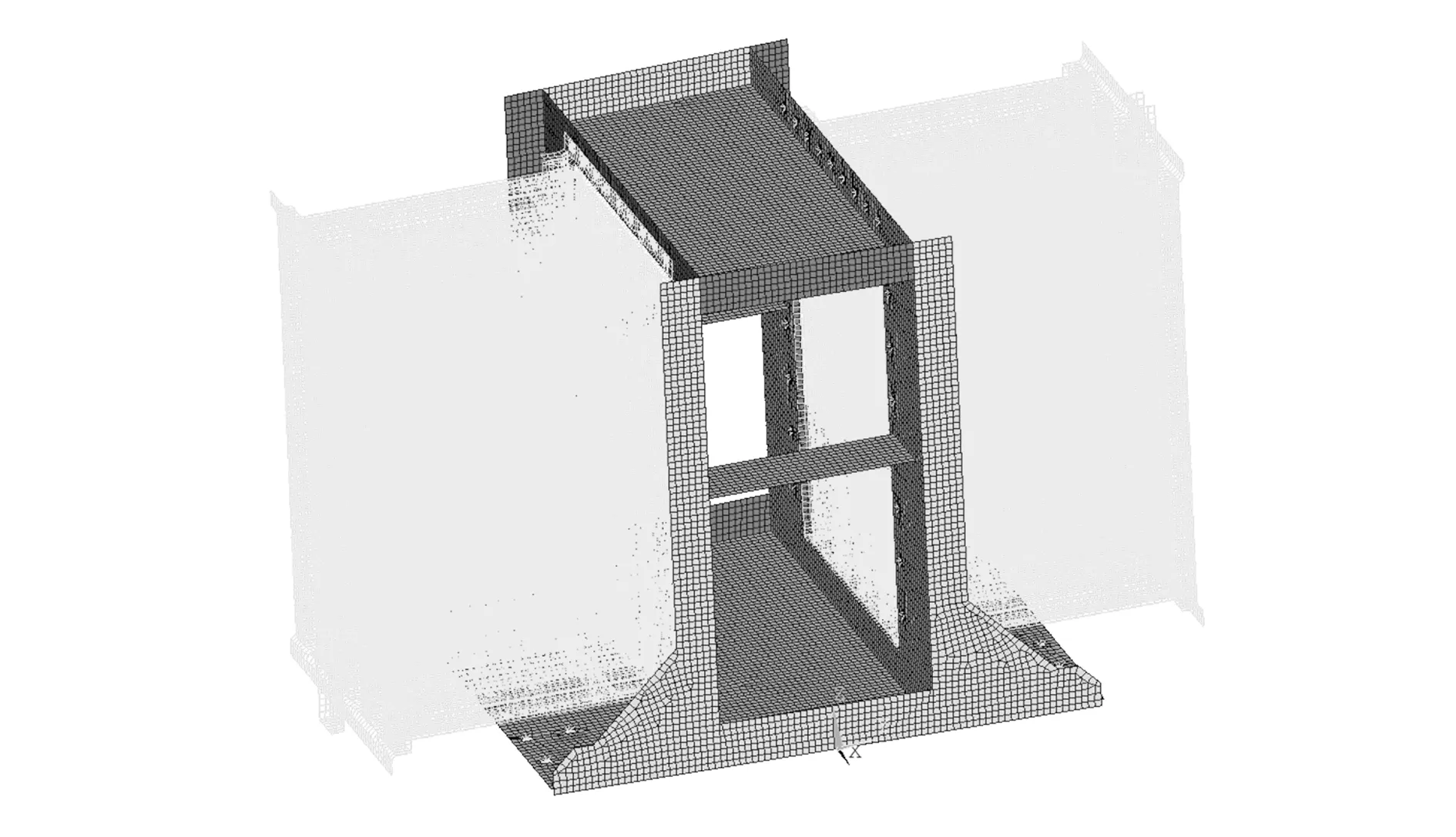
图3 超单元构成的有限元模型

为了比较超单元方法与传统方法在求解效率和精度上的差异，本文开展了超单元方法与传统方法的抗震计算对比。

4 结果分析

设备的抗震分析采用反应谱分析方法，该方法是核电工程抗震分析的主要方法之一。由于设备的平面布置方位与反应谱方向不确定，水平方向反应谱数据采用X向和Y向包络谱，反应谱曲线如图4所示。

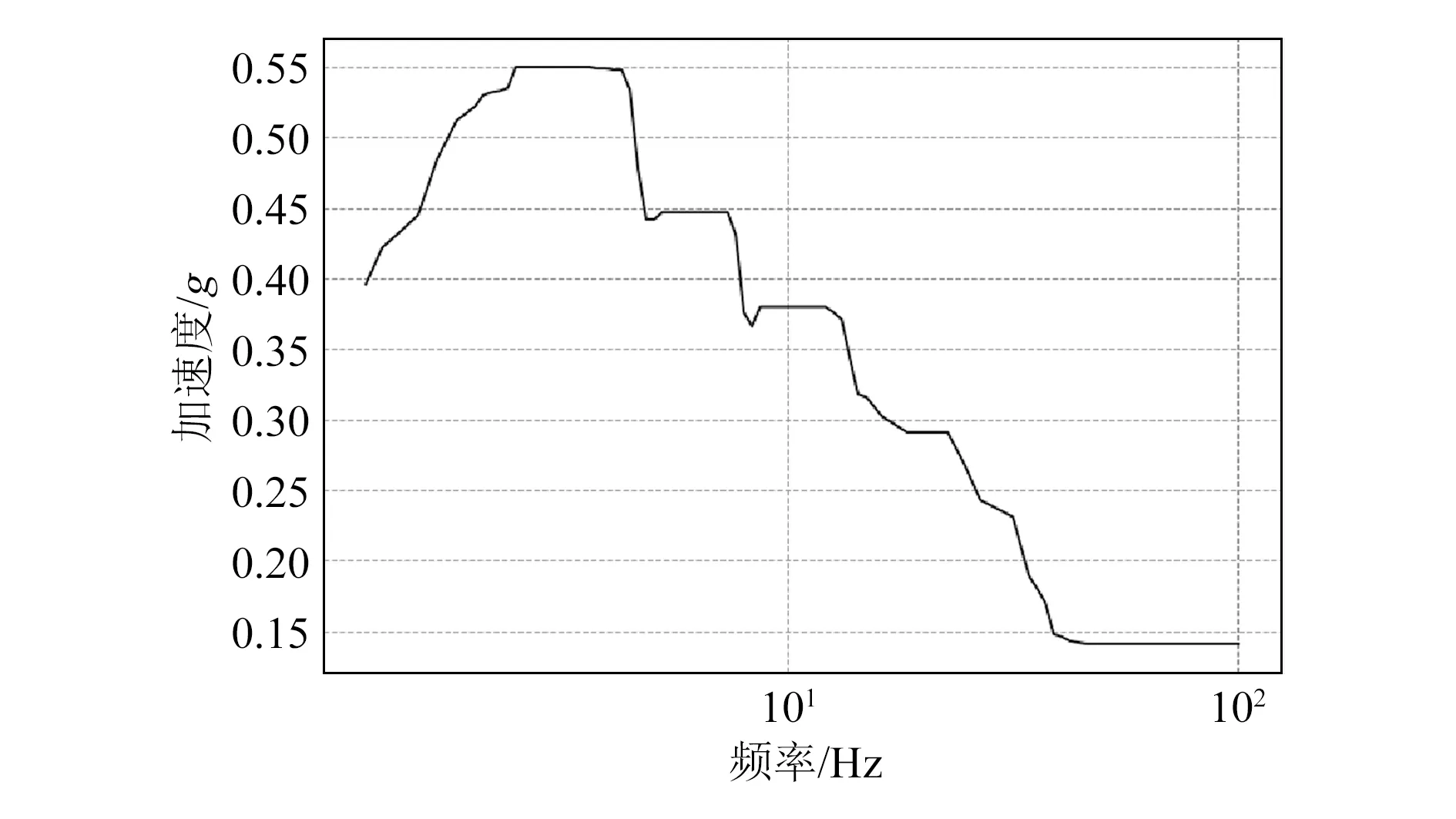
图4 水平方向的输入反应谱数据

如图5和图6所示，计算得到的模型1阶模态振型为Y向的摆动。由于未对超单元结果进行扩展，图6未显示滤网的振型结果。

图5 传统方法1阶模态振型

图6 超单元方法1阶模态振型

通过模态分析，可得到两种模型前3阶主频和参与质量的分配情况，见表1和表2。由表可以看出,2种方法频率结果近乎一致，3个方向的参与质量也基本一致，由此可知超单元方法在精度上满足工程要求。

表1 传统方法模型的模态频率和参与质量

表2 超单元方法模型的模态频率和参与质量

表3列出了2种方法在Y向地震载荷的底部基础反力结果，可以看出2种方法在Y向的结果相差不到5%。表中FX,FY,FZ分别为基础点在X,Y,Z方向的受力，MX,MY,MZ分别为基础点在X,Y,Z方向的弯矩。

表3 2种方法的基础载荷对比

为比较2种方法在计算时间和结果数据上的差异，在24 GB内存、Intel i7处理器的微型计算机上开展计算，以Y向的反应谱分析计算为例，时间跨度为从模态求解提交开始到反应谱分析求解结束。

从表4可以看出，超单元方法求解时间较短，能够节省大量计算时间。若遇到多次迭代计算的情况，更能体现该方法的优势；此外因为超单元方法未对超单元滤网结构的结果进行扩展，所以结果数据量远小于传统方法，能够节省计算空间。

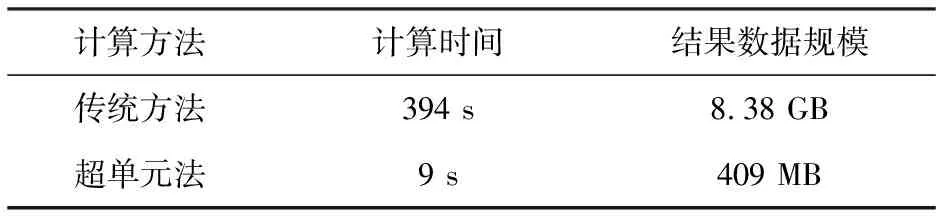
表4 2种方法的计算时间和结果大小对比

正是基于以上优点，笔者在对过滤器模块的框架进行优化时，利用超单元方法迅速给出计算结果，后续对支撑框架的厚度进行了优化，并且相较初始设计增加了框架中间支撑筋板，如图2所示，采用超单元方法大大提高了计算效率，满足了工程设计进度要求。

5 结论

针对华龙二号内置换料水箱过滤器系统过滤模块设计，本文通过比较超单元方法与传统方法在求解时效和精度方面的差异得知：超单元方法适用于设备或产品的初步力学分析，尤其适合解决多次迭代优化计算的时效问题，解决了求解耗时和需求时效的矛盾问题，是一种良好的工程实践方法。值得注意的是，本文得出的结论是基于过滤器模型，对不同的模型节省时间和计算空间的效果会变化，但节省时间和空间的趋势不会变。