电容绝缘子的场路耦合特性分析

梁 军，刘红文，黄继盛，曾宏宾，赵航俪

(1.云南电网有限责任公司临沧供电局，云南 临沧 677000)(2.云南电网有限责任公司电力科学研究院，云南 昆明 650217)

10 kV/35 kV电容绝缘子是将陶瓷电容浇铸在环氧树脂内制成的具有一定机械强度的绝缘子，具有结构简单、价格低廉的特点，在电力系统开关柜、环网柜及防误操作闭锁装置等隔离保护系统中得到了广泛应用。然而，高压线路绝缘子长期运行在强电场和有多种污秽、机械应力及高温日照、风吹雨打等恶劣环境中，易出现绝缘子内部裂隙、表面破损、阻抗降低和污闪等多种故障，严重威胁电力系统的安全运行[1-3]，因此对绝缘子检测工作的需求和重视程度越来越高。据统计，开关柜绝缘介质劣化的主要原因是局部放电，由开关柜绝缘介质劣化引起的事故占开关柜事故的85%以上。当绝缘子内部发生局部放电时，会引发一系列电磁、声光、化学等反应，基于此，研究人员开展了大量的研究，方法包括绝缘子电学检测法[4]、声学检测法[5]、光学检测法[6]及化学检测法[7]等。电场法是最为简单有效的方法之一，其原理是：将绝缘子等效成形状不规则的非均匀填充电介质，绝缘子在高电压作用下会产生微弱的泄漏电流，但泄漏的电流非常小，对电场强度的影响可以忽略不计，此时绝缘子内部电场分布较为规则，其电场分布曲线一般呈光滑的U型曲线。然而当绝缘子劣化时，由于绝缘子电介质材料在空间上的非正常分布导致其内部电场分布发生变化，因此电场法判断绝缘子是否劣化的依据是形状不规则的非均匀填充电介质在时变电磁场中的电场分布情况。

绝缘子局部放电与外加电压的类型、绝缘介质本身的材料特性、缺陷处的电场分布及放电所产生的空间电荷有着密切的关系，不同的绝缘子其内部电场分布存在较大的差异。为了揭示绝缘子正常和异常情况下其内部的电场分布规律，从理论上指导绝缘子劣化检测方法的研究，本文建立了电容绝缘子传感器的场路耦合模型，以新型陶瓷电容绝缘子传感器为研究对象，分析了其内部的电场分布特性。

1 耦合分析模型

电容绝缘子场路耦合建模的思路是，首先基于电容绝缘子在高压传输电路中的结构，建立其电路模型；其次针对电容绝缘子的非规则结构，采用有限元方法计算其电容值，并将电容值代入电路模型中计算电容两端电压；最后建立包含电容电场有限元仿真模型，将计算得到的电容电压作为激励条件加载在有限元模型中，从而实现电容电场和电路的耦合仿真。其建模方法如图1所示。

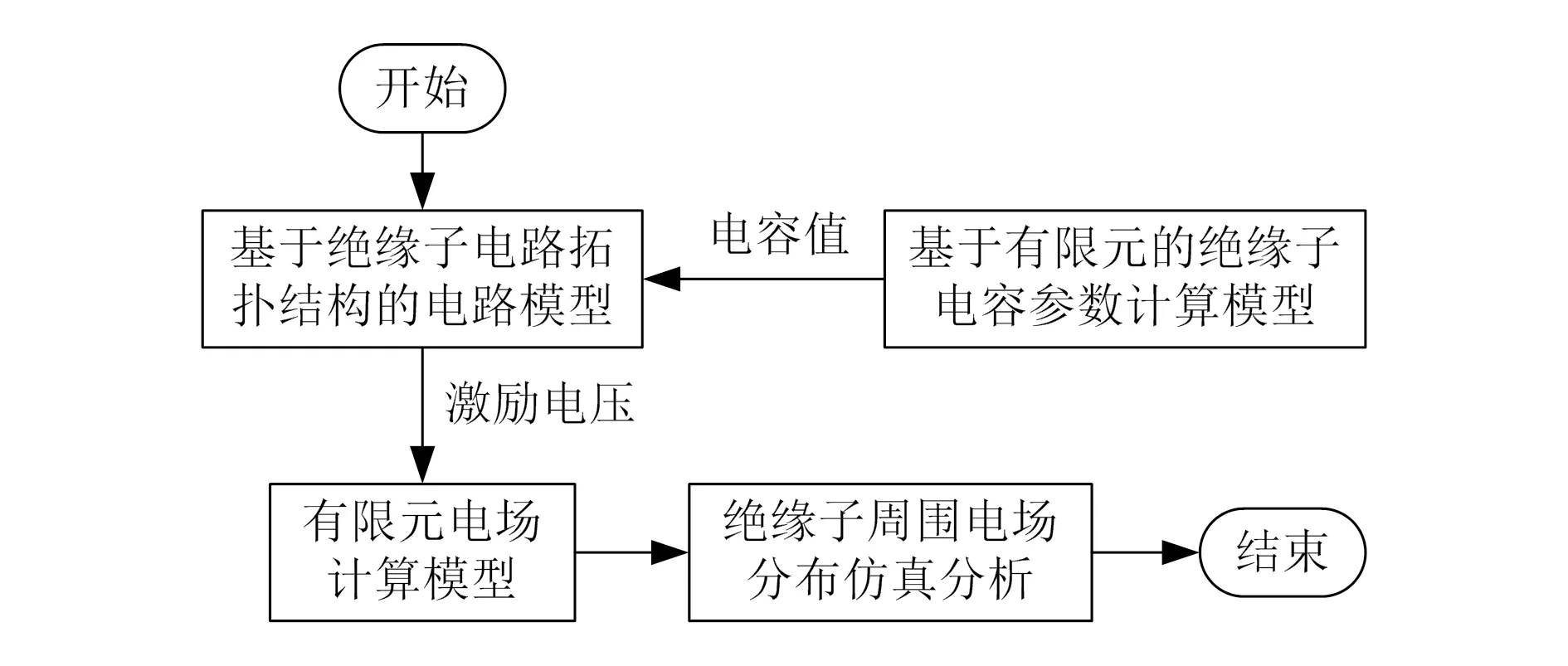
图1 电容绝缘子及其场路耦合建模方法

1.1 电路模型

本文的研究目的是通过场路耦合分析给出电容绝缘子正常和异常情况下其周围的电场分布，对比两种情况下电场的差异，为绝缘子的劣化检测提供依据。从现实需求出发，本文给出的电路建模对象为现有开关柜电容绝缘子的传感器-陶瓷电容芯绝缘子，陶瓷电容芯绝缘子被设计成具有局部放电信号耦合功能的电容(图2中的耦合电容C11)。将现有绝缘子装置的电容设计为检测阻抗，通过局部放电检测装置带电检测开关柜的局部放电信号，判断开关柜A、B、C三相局部放电情况。

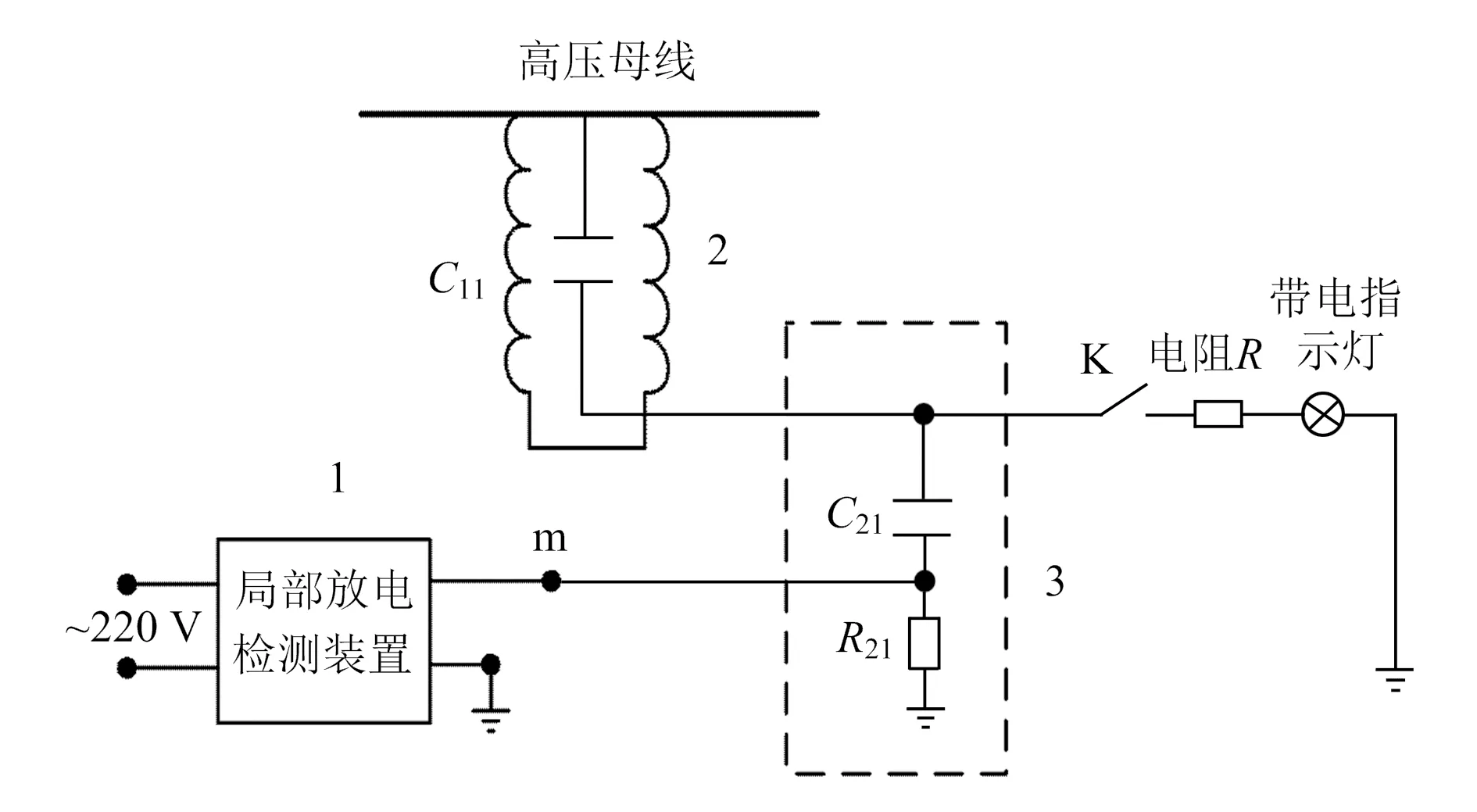
图2 电容绝缘子电路

电容绝缘子检测系统由局部放电检测装置1、陶瓷电容芯绝缘子耦合电容2及检测阻抗3构成。局部放电检测装置1与检测阻抗3电连接，用于测量开关柜局部放电信号；陶瓷电容芯绝缘子耦合电容2的高压端与母线带电部分电连接，低压端与检测阻抗3电连接。检测阻抗3安装在电容绝缘子装置中，另一端与地连接，如图2所示。

在Simulink中建立上述电路模型，如图3所示，其中C2=5 pF，R1=R2=1 nΩ，电压源为20 kV工频信号。

图3 仿真电路模型图

1.2 电场计算模型

1)电容计算模型[8]。

电容为某介质结构中储存的静电能量，有以下表达式：

(1)

式中：Ue为电容器的静电储能；C为电容值；V为电容器两端的电压。从而可得电容计算公式为：

(2)

采用Ansoft静电场求解器通过一系列的静电模拟来计算电容绝缘子的电容矩阵。每一次模拟过程中，在电容器两端施加电压，其电容通过下式计算得到：

(3)

式中：D和E分别为该电容器内部电通密度和电场强度；Ω为介质的体积空间。

2)电场仿真模型[9]。

电容绝缘子的电容值一般较小，在工频电压下其阻抗较大，因此其两端电场近似为恒定电场，可采用静电场模型进行仿真分析。静电场是有源无旋场，其麦克斯韦方程组及本构关系为：

▽E=0

▽D=ρ

D=εE

(4)

式中：▽是矢量微分算符；ρ为电荷密度；ε为材料的介电常数。由矢量恒等式可知，如果一个矢量场的旋度为零，那么该矢量场可以用一个标量场的梯度表示，由此引入标量电势φ：

E=-▽φ

(5)

式(5)中的负号表示电场指向方向为电势下降最快的方向。忽略材料各向异性，由式(4)、(5)可得：

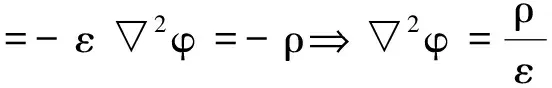
(6)

实际上，一般在介质端面加载电压激励时，对于介质以外的空气域来说,其电荷密度为0，其电场满足拉普拉斯方程，即：

▽2φ=0

(7)

且空气域与介质交界面满足：

φ=U

φ1=φ2

(8)

式中：φ1,φ2为不同介质中的电位需满足的连续条件。采用有限元方法对上述拉普拉斯方程进行离散，并代入其边界条件，即可求解介质周围空气域的电场分布，可作为电容介质裂化检测的依据。

2 仿真结果及分析

2.1 仿真条件

以图4(a)所示的绝缘子为例，介质材料为树脂，进行绝缘子场路耦合分析，图4(b)为对应的三维模型，采用电容有限元计算模型计算得到其电容值为3.06 pF。电容的劣化表征形式主要包括裂痕、烧蚀等，为建模方便，本文仅考虑电容绝缘子内部存在裂痕时的情况(伞裙破损)[10]，图4(c)为绝缘子伞裙破损时的三维模型，计算得到其电容值为3.05 pF。可见，正常情况和异常情况下，两者的电容值偏差仅为0.3%。

图4 电容绝缘子模型图

2.2 仿真结果

将计算得到的正常和异常情况下的电容绝缘子电容值代入绝缘子电路模型，得到两种情况下电容绝缘子两端的电压值变化曲线，如图5所示，由图可见，由于两种情况下电容绝缘子的电容值偏差只有0.3%，因此其两端电压基本相同，峰值电压为12.4 kV。

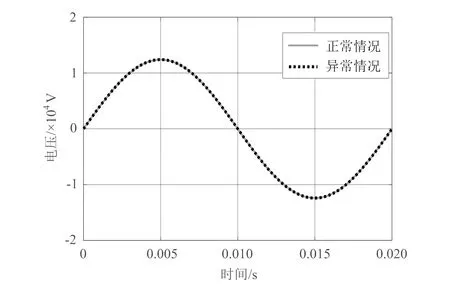
图5 电容绝缘子两端电压

进一步，将计算得到的电容绝缘子两端电压代入电场有限元计算模型中，计算得到两种情况下的电场强度分布云图，以及距离电容中轴线50 mm处轴线上的电场强度变化规律，如图6所示，可见正常情况下绝缘子两端电场呈U型分布，在伞裙破损位置处电场有较大的波动，通过识别该波动信号即可判断电容绝缘子存在缺陷。

图6 电容绝缘子中间电场分布

图7给出了电容绝缘子中心截面的电场强度分布云图，由图可见，在伞裙破损位置处电场强度云图有明显的缺失，通过电场扫描设备也可以判断缺陷所在位置。

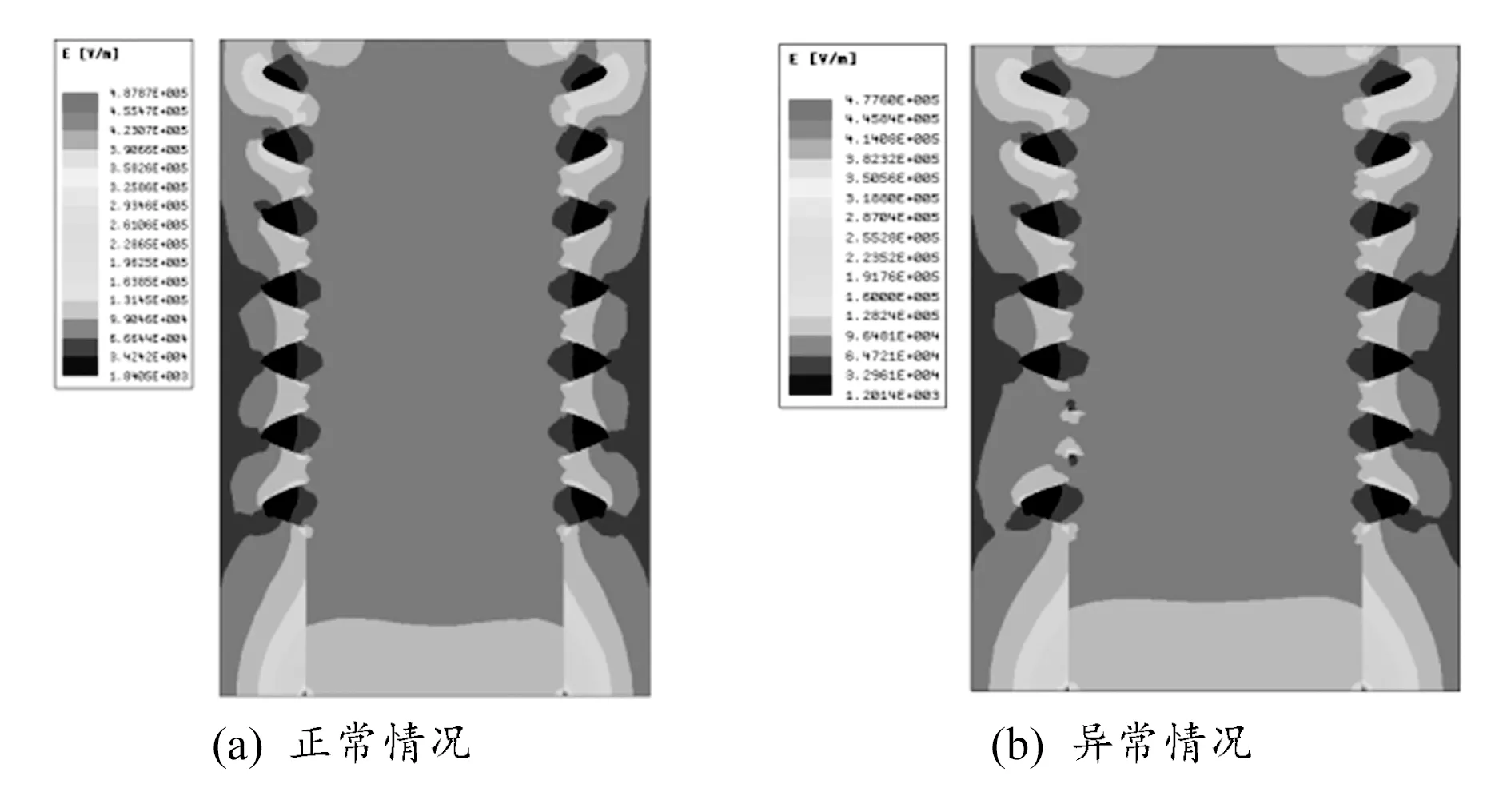
图7 电容绝缘子中心截面电场分布云图

综上所述，从仿真结果可以看出，异常时电容绝缘子电场强度在缺陷位置会有较大变化，可为电容绝缘子劣化检测方法提供强有力的设计依据。

3 结束语

本文针对电容绝缘子的内部结构和电气结构，建立了电容绝缘子的电场和电路耦合分析模型，仿真分析了电容绝缘子结构正常以及伞裙存在破损时的电容值变化以及引起的内部电场强度分布的变化。仿真结果表明：由电容绝缘子局部缺陷引起的宏观电容参数值变化较小，但是反映在局部微观的电场变化非常明显，可以通过检测局部电场的突变信号来判断绝缘子的缺陷位置。本文的电容绝缘子的场路耦合分析方法，在电容绝缘子的劣化研究中具有良好的工程应用价值。在本文的基础上，可进一步研究不同绝缘缺陷类型和分布特征对电容绝缘子劣化特性的影响。