精细神经网络仿真方法研究进展
张祎晨,黄铁军,2*
1.北京大学计算机学院,北京 100871; 2.北京大学人工智能研究院,北京 100871
0 引 言
理解大脑神经元的信息处理机制和计算原理是脑科学领域最重要的问题之一。大脑不同脑区的神经元具有很高的复杂性。不同于现有人工神经网络中的点神经元模型,生物大脑中单个神经元具有非常复杂的结构,这种复杂结构称为树突。大量研究工作表明树突在信息处理中表现出很强的非线性(Stuart和Sakmann,1994;Schiller等,1997;Larkum等,1999;Schiller等,2000)。这种非线性特性对大脑神经元实现不同的信息处理功能有着重要作用(Payeur等,2019;Gidon等,2020;Poirazi和Papoutsi,2020)。由于实验条件的限制,人们对于树突的计算机理及其在神经环路信息处理中的作用与机制了解仍然十分有限。建模仿真可以在实验限制之外帮助人们理解大脑的计算机理。
精细神经元模型(Rall,1962;Segev和Rall,1988)对真实神经元树突的信息处理过程进行模拟,可对真实大脑神经元的生物物理反应过程进行仿真,在实验条件限制之外对树突信息处理过程进行探索,是帮助人们理解树突计算机理的重要方式。
精细神经网络仿真帮助理解神经环路功能背后的实现机理。当仿真规模从单个神经元扩大到网络时,神经环路和大规模神经网络模型可以实现从离子通道到网络动力学的多尺度仿真(Markram等,2015;Migliore等,2015;Billeh等,2020;Hjorth等,2020)。由于现有实验条件无法实现从离子通道到网络尺度的同时测量,因此大规模精细神经网络仿真可以帮助科学家摆脱实验条件的限制,对神经环路的信息处理过程以及功能进行理论分析,对于理解神经环路功能背后的机理具有重要作用(Einevoll等,2019)。
除了可以帮助科学家理解神经元树突的计算机理以及大脑神经环路功能背后的机制,精细神经元以及精细神经网络模型可能启发新型类脑智能算法(黄铁军 等,2016;曾毅 等,2016)。
精细神经元所具有的强大计算能力使其在处理人工智能相关任务时表现出强大的可能性。由于树突在神经元信息处理中的非线性特性,单个精细神经元模型的响应需要多层人工神经网络才能拟合,表明单个精细神经元的计算能力与多层人工神经网络相当(Poirazi和Mel,2001;Häusser和Mel,2003;Poirazi等,2003;Beniaguev等,2021)。因此,一些复杂任务只需要单个精细神经元就可以完成,例如求解异或问题(Gidon等,2020)、信号的时空滤波等(Payeur等,2019)。
精细神经网络学习过程仿真为精细神经元模型提供了学习算法,为构建基于精细神经元的类脑智能算法提供了基础。基于精细神经元的学习算法使得精细神经元模型可以通过不断学习逐渐“学会”完成复杂任务(Moldwin和Segev,2020;Bicknell和Häusser,2021;Moldwin等,2021;Payeur等,2021),而不需要人为对模型相关参数进行调试。此外,精细神经网络学习过程仿真可以帮助科学家理解大脑学习机制(Urbanczik和Senn,2014;Bono和Clopath,2017;Sacramento等,2018;Lillicrap等,2020)。对大脑学习机制的深入理解可能启发更强的人工智能算法(Hassabis等,2017;Chavlis和Poirazi,2021)。
综上,结合精细神经元强大的计算能力以及精细神经元上的学习方法,精细神经网络在构建新型类脑智能模型、启发新型人工智能算法方面展现出强大的可能性。
精细神经元仿真对脑科学和人工智能领域的研究均有重要作用。由于精细神经元模型包含复杂的生理特性,其模型方程不存在解析解,只能通过仿真的方式得到模型在给定刺激下的响应。然而,精细神经元仿真需要进行大量计算,巨大的计算量给相关研究工作带来了很大的挑战。
精细神经元建模的理论基础主要包括Hodgkin和Huxley于1952年提出的 HH 模型(Hodgkin和Huxley,1952)以及Rall于1959年提出的电缆理论(cable theory)(Rall,1959)。HH模型通过一组常微分方程建模神经元各位点离子通道产生的电流;电缆理论使用偏微分方程建模不同位点间响应的相互影响 (图1)。
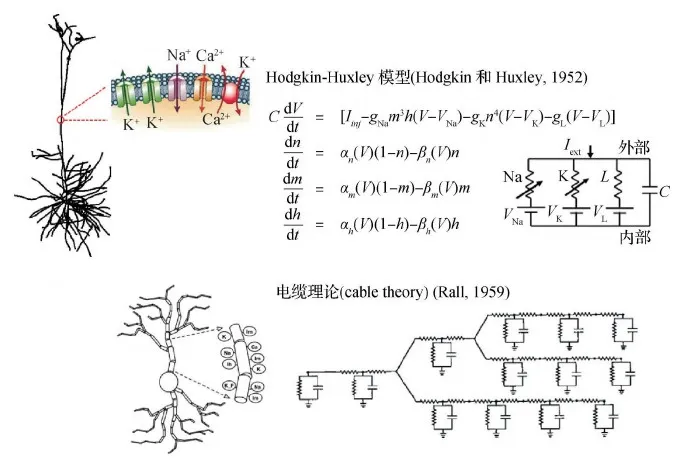
图1 精细神经元模型(Kumbhar等, 2019)
综合HH模型与电缆理论,精细神经元模型可用偏微分方程描述为
(1)
式中,cm表示神经元细胞膜的电容值,v(t,x) 表示神经元各个位置以及各个时刻的电压值,ion(v(t,x)) 表示离子通道产生的电流,通常为HH模型及其变种。通过建模各位点的电流响应,精细神经元模型可对树突的信息处理过程进行建模。使用数值方法求解上述方程的过程称为仿真。在实际中通常将单个神经元划分为成百上千个计算单元,这给仿真带来了巨大的计算量。
如何对精细神经元以及精细神经网络模型进行高效仿真是一个经典的研究问题。本文对精细仿真方法相关研究工作进行总结与梳理,从以下4个方面总结了相关方法(图2):1)主流仿真平台与核心仿真算法;2)网络尺度并行仿真算法;3)神经元尺度并行仿真算法;4)基于GPU(graphics processing unit)的并行仿真算法。通过对现有方法进行分析,本文进一步对精细神经元仿真方法的未来研究方向进行展望。
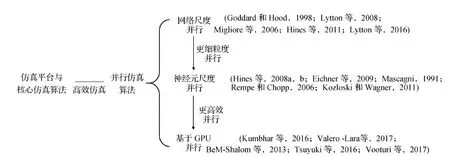
图2 本文组织架构
1 精细仿真平台与核心仿真方法
精细神经元仿真的本质是使用数值方法对精细神经元模型对应的偏微分方程进行求解。精细神经元仿真平台对仿真过程的实现进行封装,使用户可以不必了解仿真过程,专注于模型的构建。精细神经元仿真平台是精细神经元仿真、建模的基础。本节将对精细神经元仿真平台和平台中使用的数值仿真方法进行介绍。
1.1 精细仿真平台
GENESIS(Bower和Beeman,1998)是早期发布的经典仿真平台,支持精细神经元的建模仿真。NEURON(Hines和Carnevale,1997)是国际上最主流的通用神经计算仿真平台,在最大的神经元模型数据库 ModelDB(McDougal等,2017)中 80% 的模型均使用NEURON 实现(Tikidji-Hamburyan等,2017)(图3)。由于 NEURON 与 GENESIS 的开发时间较早,只能支持 CPU 硬件平台的仿真,且对于存储以及计算的优化相对较差,因此在进行大规模精细神经网络仿真时需要的存储及计算资源较多且仿真效率较低。
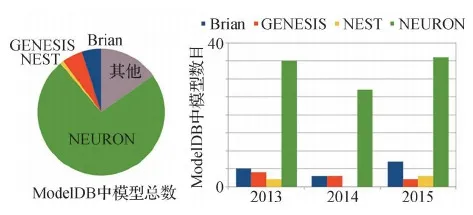
图3 各仿真平台使用情况(Tikidji-Hamburyan等,2017)
GPU逐渐应用于精细神经仿真中。GPU 由于其强大的计算能力广泛应用于科学计算、深度学习等领域(NVIDIA,2021)。为满足大规模网络仿真时的存储和计算效率要求,越来越多的平台使用 GPU 对精细神经网络进行仿真(Akar等,2019;Kumbhar等,2019;Ben-Shalom等,2022)。CoreNEURON(Kumbhar等,2019) 对 NEURON 的引擎进行了存储和计算效率上的优化,降低仿真所需内存并提高了仿真效率。此外,CoreNEURON支持使用GPU进行仿真,并针对仿真计算过程进一步优化,利用GPU强大的计算能力大幅提高了仿真效率。Arbor(Akar等,2019)同样是一款支持GPU的精细神经元仿真平台,通过针对多核CPU 以及 GPU 的优化提高仿真效率。NeuroGPU(Ben-Shalom等,2022)相比 CoreNEURON 和 Arbor 使用更细粒度的并行算法对仿真进行加速,效率更高,但仿真准确性有所下降。
1.2 核心仿真方法
1.2.1 精细仿真整体过程
当前仿真平台均使用隐式有限差分法对偏微分方程式(1)进行求解。虽然实现上有所不同,其核心方法以及整体流程一致。隐式方法对方程中的位置电压使用未来时刻的电压值替代。对式(1)中的微分项使用差分项替换,可得
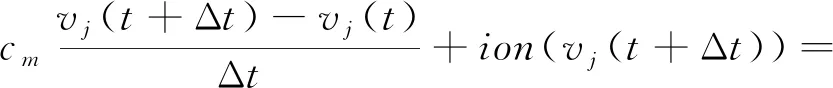
(2)
式中,Δt表示离散所使用的时间步长,Δx表示空间步长,j表示空间离散化后计算单元的编号。式(2)等号左侧差分项用于逼近v关于时间t的偏导,等号右侧差分项用于逼近v关于空间x的偏导。为求解各时刻的电压值,需要得到v(t+Δt) 与v(t)的递推关系。然而,式(2)无法直接得到递推关系,因此需要对式(2)进行一系列变换。经过一系列推导后,可以得到线性方程组,即
MΔv=r
(3)
式中,M表示由神经元动力学(包括离子通道电流、突触电流)以及不同计算单元之间电流的相互影响产生的系数矩阵,由于电流只在相邻计算节点之间流动,因此M为稀疏的伪三对角线矩阵(图4),只在相邻计算单元对应位置的值不为0;Δv表示所有计算单元的电压增量组成的向量;r为方程组右值向量,由神经元动力学产生的电流所组成。求解线性方程组式(2),即可得到所有计算单元的电压增量,由此可以得到下一时刻各计算单元的电压值v(t+Δt) =v(t)+Δv。
由上述数值方法可知,精细神经元的仿真过程步骤如下(图4):
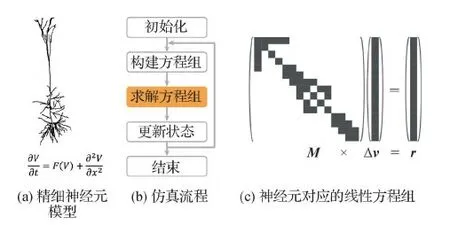
图4 精细神经元模型与仿真流程
1)给定神经元模型各计算单元的电压初值;
2)根据当前各计算单元的电压计算初始离子通道电流、各位点的轴向电流等值,并由这些值构造线性方程组式(3);
3)通过求解线性方程组式(3),得到所有计算单元的电压增量;
4)根据电压增量更新所有电压值得到下一时刻的电压。
以上步骤2)—4)迭代进行,最终可以得到模型所有计算单元在各时刻的电压值,即式(1)的数值解。整体仿真过程中,求解线性方程组的计算复杂度为O(n3),n表示每个神经元所包含的计算单元数目,为整个仿真过程的瓶颈。
1.2.2 Hines算法
为解决精细神经元仿真中求解方程组计算量过大的问题,Hines(1984)提出一种高效求解算法,称为Hines算法。Hines算法利用方程组的系数矩阵为伪三对角线稀疏矩阵这一特性,使用特殊的高斯消元法对方程组进行求解,将求解方程组的计算复杂度从O(n3)降低为O(2n),如算法1所示。由于计算复杂度低且仿真精度高,Hines算法成为主流仿真平台的核心算法。
算法1 Hines算法 (Valero-Lara等,2017)
1) void solveHines(double *u, double *l, double *d, double *rhs, int *p, intcellSize)
//u: 上对角线元素,l: 下对角线元素,d:对角线元素,*表示指针,rhs: 方程组右值,p:父节点,cellSize:元素数目
2) inti;
3) doublefactor;
4) // 三角化过程
5) fori=cellSize-1→ 0 do
6)factor=u[i]/d[i];
7)d[p[i]] -=factor*l[i]; // 消元
8)rhs[p[i]] -=factor*rhs[i]; // 消元
9) end for;
10)rhs[0] /=d[0];
11) // 回代过程
12) fori= 1 →cellSize-1 do
13)rhs[i] -=l[i] *rhs[p[i]];
14)rhs[i]/=d[i];
15) end for。
1.3 小结
现有仿真平台均使用隐式有限差分法对精细神经元进行仿真。Hines算法因其计算效率与仿真精度成为现有平台的核心仿真算法。尽管Hines算法在求解线性方程组中有很高的计算效率,但当建模较为精细时,计算复杂度依然很大。尤其在进行大规模网络仿真时,由于网络包含大量计算单元,使用Hines算法进行仿真耗时过长。同时由于模型较为复杂,现有神经形态硬件无法支持精细神经元模型的仿真。为解决仿真效率这一问题,相关工作尝试使用并行的方式对精细神经网络进行仿真。
2 网络尺度并行仿真方法
网络尺度并行主要用于精细神经网络仿真。由于各神经元求解线性方程组的计算互不影响,因此不同神经元的计算可以并行执行。网络尺度并行方法的主要思想是通过对网络进行划分,使每一物理计算核负责一组若干神经元模型的计算(图5),从而充分利用硬件计算资源提升网络仿真效率。

图5 CPU上的网络尺度并行方法
PGENESIS是经典仿真平台GENESIS的并行版本,通过网络尺度并行的方式使得GENESIS平台可以利用并行的方式进行大规模网络仿真(Goddard和Hood,1998)。
主流仿真平台NEURON同样支持网络尺度并行(Migliore等,2006;Lytton等,2008)。进行大规模网络仿真时,整个网络划分到不同的硬件处理单元,通过多进程的方式进行并行。仿真中,各进程对网络中的各神经元进行计算,并对神经元产生的脉冲发放信号进行通信,不同进程上神经元产生的脉冲发放信号通过消息传递接口(message passing interface,MPI)传输(图6)。Hines等人(2011)进一步对比了MPI通信的不同实现方式对仿真性能的影响。借助NEURON上的网络尺度并行方法,Lytton等人(2016)探究了使用不同数目的计算节点对不同类型、不同规模的网络进行仿真时的运行效率。实验结果表明网络尺度并行方法有很好的可扩展性,可以充分利用已有计算资源对大规模网络进行仿真。
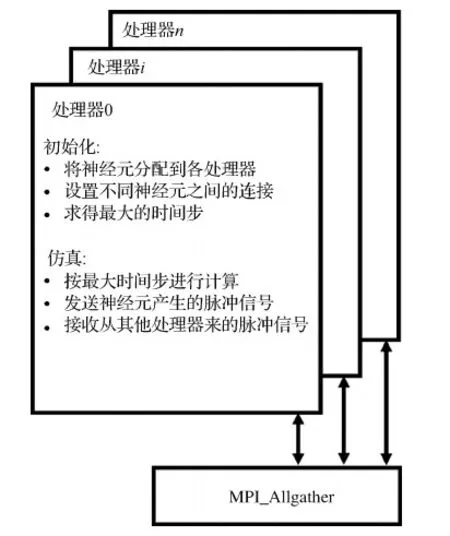
图6 NEURON中网络尺度并行算法(Migliore等,2006)
为进一步提升NEURON在大规模仿真时的计算效率,Kumbhar等人(2016)对NEURON的计算过程进行优化。不同于NEURON使用MPI的进程级并行,Kumbhar等人(2016)使用更轻量的线程级并行,效率更高。实验表明,使用线程级并行可将仿真效率提升约12%。此外,Kumbhar等人(2016)对NEURON中的数据存储方式进行优化,对计算时的数据进行向量化存储(图7),提升存储带宽,进一步提升仿真计算效率。
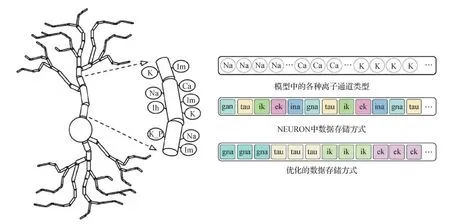
图7 优化数据存储(Kumbhar等,2016)
由于线程级并行有着较高的仿真效率,Valero-Lara等人(2019)进一步提出同时使用多线程与多进程的网络尺度并行方法,使用MPI+OpenMP的实现方式对大规模网络进行仿真。为进一步提升仿真效率,Valero-Lara等人(2019)对如何同时进行计算与通信进行了探索。
网络尺度并行方法对不同神经元的计算进行并行,对大规模网络的仿真有显著的效率提升。网络尺度并行方法通过充分利用多核CPU、计算集群的算力,提高仿真中方程组求解以及整个仿真过程的效率。经典仿真平台NEURON与GENESIS已集成相关网络尺度并行方法,支持使用计算集群或超级计算机进行大规模网络的仿真。
然而,对于每个神经元自身的方程组求解,网络尺度并行方法依旧使用Hines算法串行进行,导致当网络中单神经元模型较为复杂时(例如包含上千计算单元的CA1模型(Migliore等,2004)、purkinje模型(Masoli等,2015),包含几万计算单元的树突棘尺度模型等),单个神经元对应方程组的求解需要大量计算,耗时过长,网络尺度并行无法取得令人满意的性能提升。为进一步提升仿真效率,相关工作提出神经元尺度的并行仿真方法。
3 神经元尺度并行仿真方法
神经元尺度并行方法对每个神经元内的求解线性方程组计算进行并行。相比于网络尺度的并行方法,神经元尺度并行粒度更细,并且可与网络尺度并行同时使用,以进一步提升仿真性能。然而,神经元内部的方程组求解存在大量依赖关系,如何对其进行并行是一个需要研究的问题。为了使神经元内部计算可以并行,现有方法主要使用以下两种策略:1)神经元划分并行,将神经元划分为若干子块,对不同子块中不存在依赖关系的部分进行并行;2)基于关键值近似的并行,对关键计算节点的值进行近似增大并行度,从而进一步提升计算效率。
3.1 神经元划分并行方法
神经元不同分支上的节点计算互相独立是神经元尺度并行的主要依据。由 Hines算法的实现过程可知,神经元模型中相连的计算节点之间存在计算的依赖关系,而不同分支上的节点计算相互独立,存在可并行性。
将神经元划分为若干子块是一种简单有效的并行方式。Hines等人于2008年提出了名为 neuron splitting(Hines等,2008a)和multi-split(Hines等,2008b)的方法,将神经元划分为若干部分进行计算。其中,neuron splitting(Hines等,2008a)提出在计算时可将神经元模型划分为两部分进行并行,只需要额外付出少量的数据传输代价,就可以在不影响计算精度的情况下提高计算效率。multi-split(Hines等,2008b)对模型进行进一步划分,给出了将神经元模型划分为多个子块后的并行计算方式(图8)。相比neuron splitting将模型划分为两部分,multi-split 有更大的并行度,但同时也需要付出更多额外的计算和数据传输代价。NEURON 平台已经集成了 multi-split 方法供用户直接使用。然而,multi-split 方法需要用户人为对神经元进行划分,因此划分策略对效率有很大影响。

图8 multi-split方法(Hines等,2008b)
Eichner等人(2009)提出的基于多核CPU的仿真方法同样使用了multi-split对神经元的计算进行并行。为进一步提升并行度,该方法对神经元各计算节点进行重新编号,改变方程组求解时的依赖关系,使得可并行子块数目增多,以此提高计算效率。
然而,由于求解线性方程组的计算中各神经元计算节点之间的依赖关系,划分子块的方式虽然可以在一定程度上并行,但子块连接处的节点需要在与其相连的子块均完成计算后才能进行计算,导致部分子块需要等待其他子块完成计算后才能进行计算,并行度低,影响计算效率。
3.2 基于关键节点近似的并行方法
为提高可并行度,部分方法对关键节点的值进行近似,消除部分节点之间的依赖关系。例如,Mascagni(1991)对神经元两分支连接处的关键节点值进行假设,将原本无法并行的部分进行并行,完成分支的计算后再根据各分支的计算结果对原本假设的关键节点值进行求解,得到最终计算结果。然而,该方法需要首先使用假设值求解方程组,然后进行假设值节点的计算,相比传统的直接求解方程组需要进行额外计算。
Rempe和Chopp(2006)首先通过显式方法对各分支连接处节点的值进行近似,有了连接处节点的值后,对各分支的计算进行并行,再根据计算结果对预测值进行修正(图9)。这种方式可以大幅提高并行度,然而,神经元中包含大量连接节点,对所有连接节点均进行近似会引入较大误差。Kozloski和Wagner(2011)将Rempe和Chopp(2006)方法与Hines算法相结合,只对部分连接处节点使用显式方法进行近似,以提升仿真精度。
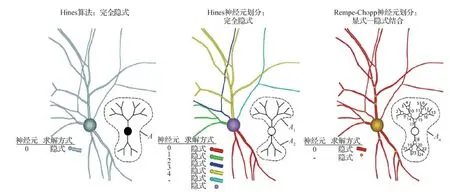
图9 不同类型求解方法示意(Kozloski和Wagner,2011)
虽然这种对关键计算节点进行近似的方法可以增大神经元的并行度,但近似会带来结果的不准确,且部分方法需要引入额外的计算量,影响计算效率。
3.3 小结
神经元尺度并行方法对神经元内部计算进一步进行并行,理论上比网络尺度并行有更高的计算效率。然而,当前神经元尺度的并行方法存在精度以及计算效率方面的问题。现有神经元划分的方法着重解决划分之后如何计算的问题,对于划分策略没有进行过多研究,导致用户在实际使用时往往需要人为进行划分,计算效率较低。基于关键节点近似的并行方法由于近似值导致结果不够精确,此外,这类方法为增大并行度,往往需要引入额外的计算,影响计算效率。
4 基于GPU的并行仿真方法
GPU因为其强大的算力在高性能计算中得到广泛使用(NVIDIA,2021),同样得以用于精细神经元并行方法上,大幅提升了精细神经网络的仿真效率。基于GPU的并行仿真方法大体也可分为网络尺度并行和神经元尺度并行两类。网络尺度并行对不同神经元的计算进行并行;神经元尺度并行进一步对各神经元内部的计算进行并行。
4.1 基于GPU的网络尺度并行方法
网络尺度并行是 GPU 上使用的主流方法。由于网络尺度并行相对容易保证计算精度,相关研究工作提出基于GPU的网络尺度并行方法。GPU 上的网络尺度并行方法核心思想与 CPU 上的并行方法类似,均利用神经元之间计算互相独立的特点对每个神经元的计算进行并行。不同点在于由于 GPU 拥有大量的物理计算单元,因此通常情况下每个线程负责一个神经元的计算(图10)。
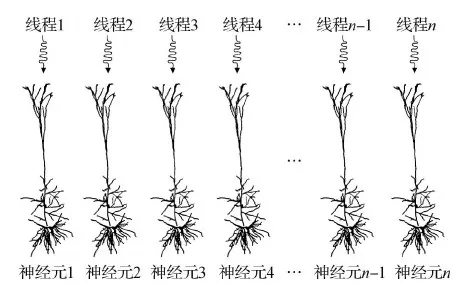
图10 基于GPU的网络尺度并行方法
针对 GPU 的硬件特性对方法实现进行优化可以充分利用 GPU 的硬件资源,进一步提升计算效率。Kumbhar等人(2016)在对NEURON计算过程进行优化的基础上进一步实现了GPU上的网络尺度并行仿真,并针对GPU进行优化,提升计算效率。Valero-Lara等人(2017)提出了 Hines算法的并行方法 cuHinesBatch,并比较了不同数据存储方式对该算法在GPU上计算效率的影响(图11),相比于经典串行 Hines算法,其计算效率提高超过一个量级。
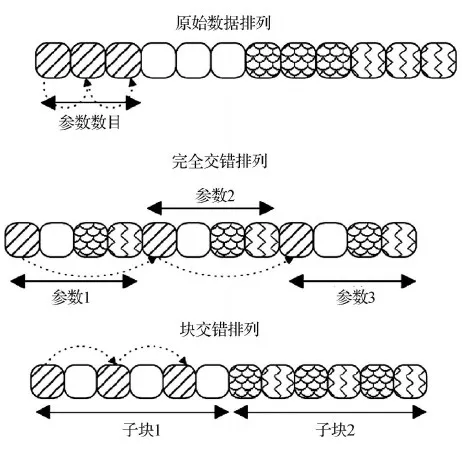
图11 不同数据排列方式对比(Valero-Lara等,2017)

4.2 基于GPU的神经元尺度并行方法
与CPU上的神经元尺度并行方法类似,相关工作提出基于GPU的神经元尺度并行方法,对神经元内部的计算进一步并行,利用GPU强大的并行计算能力进一步提升仿真效率。
Ben-Shalom等人(2013)于2013年提出使用 GPU 对神经元内部的方程组求解进行加速,他们使用Stone方法(Stone,1973)对求解过程进行并行化,并在 GPU 上进行实现(图12)。然而,由于Stone方法的使用,Ben-Shalom等人(2013)的方法虽然提高了整体计算过程的并行度,但是在仿真中引入了额外的计算,将原本 8n的计算量提升到了 20nlog2n。这种额外的计算影响计算效率,且在仿真时容易产生计算误差。实验表明,Ben-Shalom等人(2013)方法的计算结果相比Hines算法有一定误差。基于此方法,Ben-Shalom等人(2022)进一步开发了支持神经元尺度并行的 GPU 仿真平台 NeuronGPU(Ben-Shalom等,2022)。同样地,NeuronGPU在仿真时也存在误差。
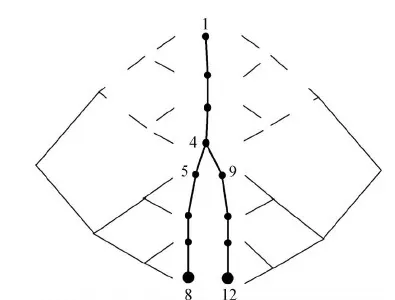
图12 Ben-Shalom等人(2013)的GPU并行方法
Tsuyuki等人(2016)使用 NVIDIA 提供的稀疏矩阵加速库 cuSPARSE,在GPU上实现共轭梯度算法对方程组进行求解。由于共轭梯度算法是一种迭代算法,使用其进行求解需要重复多次矩阵—向量相乘的计算,相比Hines算法直接求解方程组引入了额外的计算量且影响精度。Vooturi等人(2017)通过对方程组系数矩阵进行分解提高并行度,并利用 GPU 对计算进行加速,同样由于引入了额外计算,影响计算效率。Huber(2018)利用 GPU大量的计算单元对神经元的每一分支分配一个线程进行计算。然而由于神经元包含的分支数量可以达到几百,因此对网络进行仿真时,过多的线程数目导致的线程空等以及调度会带来额外开销,影响效率,且随着网络规模增大效率下降明显。
4.3 小结
基于GPU的并行仿真方法利用GPU强大的计算能力可以大幅提升精细神经网络仿真效率。网络尺度并行方法是GPU上使用的主流方法,在提升效率的同时可以保证仿真精度。基于GPU的神经元尺度方法有更高的并行度,然而,现有该类方法存在仿真精度及引入额外计算的问题。
5 结 语
表1总结了现有主要仿真方法的核心思想以及存在的不足。虽然从1990年开始陆续有相关工作提出相关方法对精细神经元仿真计算进行加速,且近些年相关工作逐渐增多,但目前依旧没有一个精度高且效率高的仿真方法支持大规模复杂精细神经网络的高效仿真。
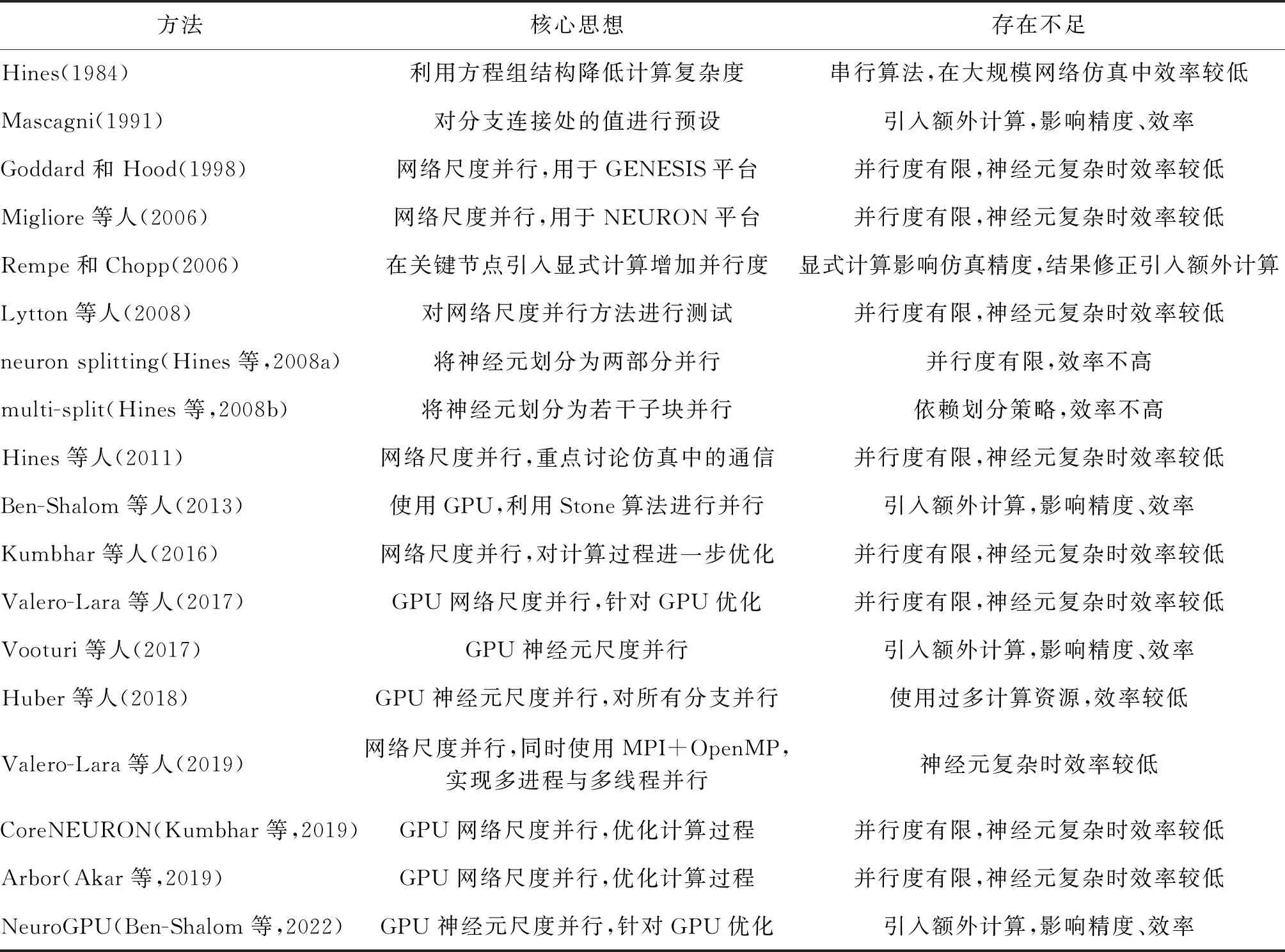
表1 不同仿真方法的特点与不足
网络尺度并行利用了不同神经元的计算互相独立的特性,将各神经元的计算进行并行,在提高效率的同时容易保证精度。网络尺度并行是精细神经网络并行仿真的基础,使得精细神经网络仿真可以在计算集群以及超级计算机上进行,使得大规模精细神经网络仿真成为可能。
神经元尺度并行方法对各神经元内部求解方程组的计算进行并行,并行粒度更细。使用更细粒度并行可以充分利用计算集群或超级计算机上的计算资源,解决网络尺度并行方法中神经元内部串行计算导致的计算效率问题。一个精确且高效的神经元尺度并行方法可以很大程度提升仿真效率,然而,当前神经元尺度的并行方法很少关注并行策略的问题,导致现有方法对神经元内部进行并行时无法取得很好的负载均衡,影响计算效率。此外,现有方法为提高并行度所引入的近似和额外计算导致计算结果不够精确,同时影响计算效率。
近年来,越来越多的工作使用GPU进行精细神经网络的仿真。GPU强大的并行计算能力大幅提升了仿真效率。GPU上的并行仿真方法整体思路与CPU方法类似,也可分为网络尺度并行和神经元尺度并行两大类。由于基于GPU的神经元尺度并行方法同样存在计算精度问题,因此网络尺度并行是GPU上主流的方法。
综上所述,现有基于CPU的并行算法无法很好地解决效率与精度的问题。GPU 的使用使得仿真效率大幅提升,然而当前基于GPU的方法以网络尺度并行为主,当单神经元模型较为复杂时效率较低。综合各类方法的特点与不足,本文认为基于GPU的神经元尺度并行方法是未来精细神经网络仿真的发展趋势。神经元尺度并行方法可以充分利用GPU强大的并行计算能力,一种基于GPU的高效且没有计算误差的神经元尺度并行方法可以有效解决当前仿真中面临的仿真效率问题。
本文回顾了精细神经网络仿真方法,从现有仿真平台及核心仿真方法出发,分别介绍了网络尺度并行仿真方法、神经元尺度并行仿真方法以及基于GPU的并行仿真方法。介绍了各类方法的核心思想与存在的不足,并对各类并行方法中一些具有代表性的工作进行了较为详细的介绍。随后对现有方法进行总结,概括了现有方法的主要贡献,并对现有方法存在的不足进行总结:现有方法在大规模网络仿真或模型较为复杂的情况下依然存在效率或仿真精度方面的问题。最后根据现有方法的特点及存在的不足,对未来研究趋势进行了展望,认为基于GPU的神经元尺度并行方法可以进一步提升大规模精细神经网络的仿真效率。

