金银花颗粒在旋风分离器中的流场数值模拟分析

苗坤宏，崔彭帝，薛启隆，于 洋*，李 正*

金银花颗粒在旋风分离器中的流场数值模拟分析

苗坤宏1, 2, 3，崔彭帝1, 2, 3，薛启隆1, 2, 3，于 洋1, 2, 3*，李 正1, 2, 3*

1. 天津中医药大学中药制药工程学院，天津 301617 2. 省部共建组分中药国家重点实验室，天津 301617 3. 现代中医药海河实验室，天津 301617

针对金银花颗粒在旋风分离器中的运动行为过程进行研究，考察不同设计参数和操作工艺条件下，颗粒在设备内部的运动过程变化规律。基于仿真模拟技术，考察受不同设备长径比、入口进气雷诺数、颗粒质量流量3个因素影响的金银花颗粒在分离器内的运动规律，并以金银花颗粒得粉率为验证指标参数，对模型可靠性进行了分析。通过仿真模拟得到了各个不同工艺条件下的金银花颗粒运动轨迹分布，计算出了对应设备的颗粒得粉率。提出金银花颗粒分离的最佳工艺建议为设备长径比5∶1，入口进气雷诺数3.23×104，颗粒质量流量80.1 mg/s，得到的金银花颗粒得粉率为96.30%。为旋风分离器内金银花颗粒的有关研究提供指导，同时改善旋风分离器在控制和设计上的不足。

旋风分离器；金银花颗粒；仿真模拟技术；运动规律；颗粒得粉率

作为我国医药工业的重要组成部分，中药工业近年来保持较快增速。随着国家对中药工业的重视程度不断提高，对于中药制药过程的研究也在不断向纵深发展[1-2]。作为气-固以及气-液两相分离重要装置的旋风分离器因其结构简单，操作弹性大，分离效率高，管理维修方便并且购置价格低廉而被广泛应用于制药工业过程中，常作为流化床反应器的内分离装置或作为预分离器使用[3]。经分离完成的固体颗粒可用于后续的制粒、压片或者制成胶囊等工艺过程。旋风分离器靠气流切向引入造成的旋转运动使得固体颗粒或者液滴因具有较大惯性离心力而被甩向外壁面实现颗粒或液滴的分离[4-5]。在旋风分离器中气体和固体颗粒的运动非常复杂，在器内任一点都有切向、径向和轴向速度，并随旋转半径变化。当进气速度过小时，设备性能无法得到充分利用；而当进气速度过大将造成严重的涡流和返混现象，影响产品质量和生产效率[6-7]。此外颗粒的质量流量与设备内部压降密切相关，过大的颗粒质量流量会导致压降减小，影响分离效率。从设备设计角度来说，不同长径比的旋风分离器在分离效率方面也出现了分离效率的明显差异[8]。为了有效评价设备的性能好坏，工业现场普遍采用旋风分离器的颗粒得粉率这一重要指标进行分析，而颗粒得粉率的高低又在一定程度上影响着中药颗粒的生产效率和生产质量，因此该指标在中药颗粒分离评价过程中的作用进一步加强。

在目前的中药生产过程中，对于旋风分离器的设计参数和工艺操作参数的控制不足，常常导致设备的颗粒得粉率难以把握，生产效率无法得到有效保证。同时由于缺乏对旋风分离器内中药颗粒运行特性的了解往往导致生产工艺及设备的设计具有盲目性。为了进一步分析操作工艺参数和设备结构对旋风分离器的颗粒得粉率影响，完成旋风分离器系统的设计优化和改造升级，实现中药颗粒的高效分离，提高生产效率，研究基于数值模拟分析对旋风分离器的入口进气雷诺数、颗粒质量流量以及设备长径比3个因素进行了考察。

1 旋风分离器结构形式

旋风分离器在设备构成上包括：进气管、排气管、排灰口以及分离器罐体[9]。本实验以某制药过程中的旋风分离器作为研究对象，其几何结构如图1所示，其中进气管管径（）为47 mm，进气管与分离器罐体顶部距离（）为50 mm，进气管长度（）为150 mm；排气管管径（e）为65 mm，排气管插入分离罐体的长度（）为97 mm，未插入分离罐体的长度（）为65 mm；分离罐体直径（）为170 mm，排灰口管径（）为54 mm，分离器罐体总高（）为510 mm，其中圆柱形罐体部分的高度（）为150 mm。

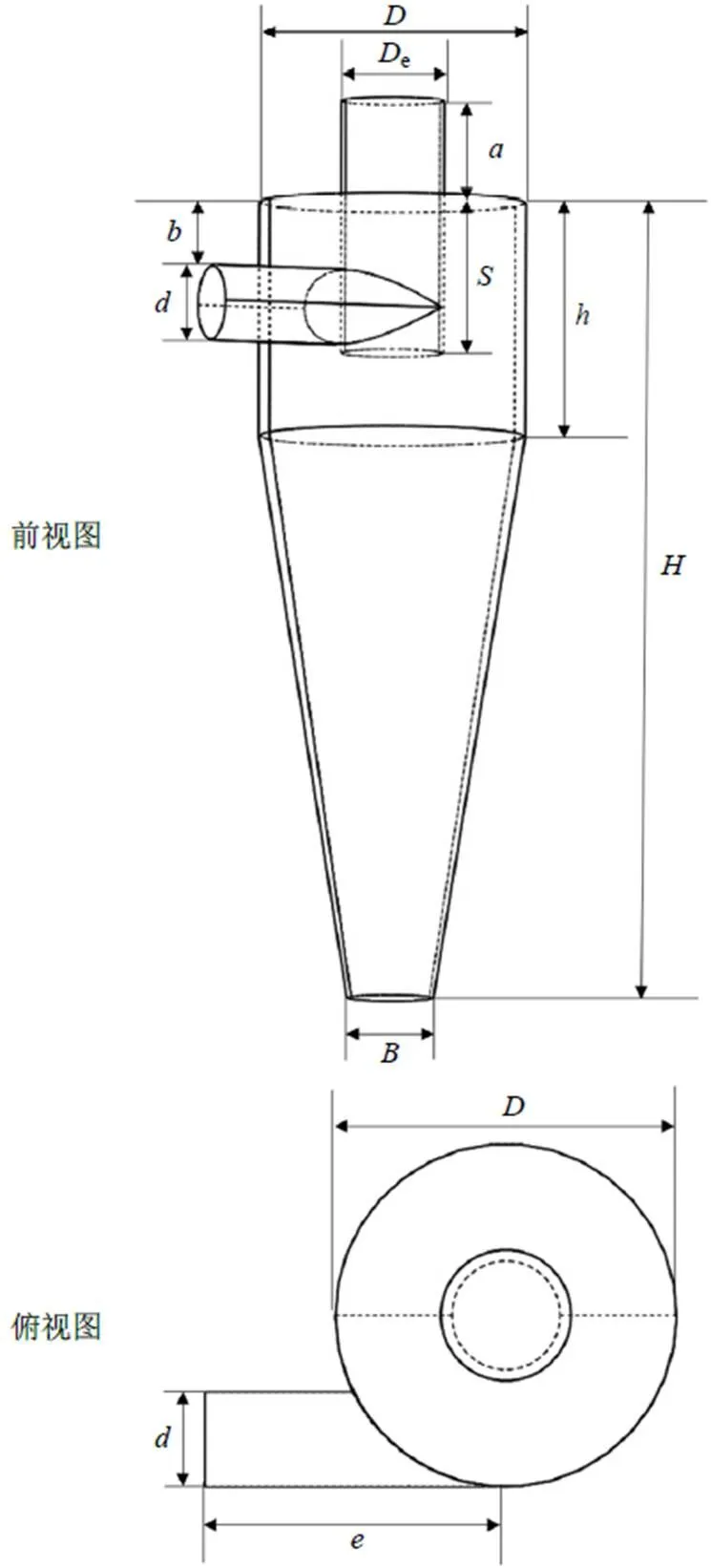
图1 旋风分离器几何结构示意图

为了考察不同长径比下旋风分离器内部粒子运动状态，研究基于实际设备尺寸（长径比∶＝3∶1），共建立了5个不同长径比的旋风分离器，建成的设备长径比∶如表1所示。

2 旋风分离器流场数值模拟

本实验基于商用模拟仿真软件平台，使用Euler- Lagrangian模型，将常温气流视为连续相，干燥颗粒视为分散相，用来分析旋风分离器内部气流与颗粒之间的相互作用。对于连续相计算而言，进气端设置为速度入口，排气端设置为压力出口，出口压力绝压为1个大气压。控制方程采用有限体积法离散，通过simple算法求解压力与速度耦合，选取差分格式为quick格式，压力插补格式为presto格式[10]。对于分散相运动过程计算而言，为了简化数值模拟分析过程，设置排气口为逃逸边界条件，固体壁面边界为无滑移全反射边界条件。

表1 不同长径比的旋风分离器设备尺寸

2.1 连续相方程

在连续相模型的守恒方程框架中，包括了连续性方程，动量守恒方程以及能量守恒方程。连续性方程如式（1）所示，动量方程如式（2）所示。

∂ρ/∂＋∇∙(ρ∙U)＝Γ,CD（1）

∂(ρ∙u)/∂＋∇∙(ρ∙u∙u)＝−∇＋∇∙＋ρ∙＋C（2）

ρ为连续相密度，U为连续相速度，为时间，Γ,CD为由连续相至离散相的质量源项，CD为连续相至离散相的受力，为重力常数，为动力压强，为黏性应力张量，u、u表示平均速度分量

对于牛顿流体，可由式（3）计算得到。

＝eff[∇u＋∇u] （3）

eff为有效黏度，可通过式（4）求得。式（4）中为黏度，t为涡动黏性。

eff＝＋t（4）

在雷诺Navier-Stokes方法中需要通过湍流建模来封闭对流加速度的非线性项。参考不同湍流模型的研究结果，本实验选用剪切应力输运（Shear-Stress Transport，SST）-2方程涡黏性数值模拟模型来模拟整个Navier-Stokes方程中固有的波动[8]。SST-模型由Menter提出[11]，该模型在边界层附近可直接计算到粘性底层，且无需额外的阻尼公式，同时该模型可有效避免入口自由来流湍流过于敏感的问题[12-13]。具体计算过程如下所示。基于SST-模型改写动量守恒方程如式（5）所示。

∂ρU/∂＋∂ρUU/∂x＝∂/∂x＋∂/∂x[(＋t)∙(∂U/∂x＋∂U/∂x)] （5）

U为第个速度分量，U为第个速度分量，x、x、x为笛卡尔坐标，为流体密度，涡动黏性由-SST模型计算得到。该模型中的方程和方程分别如下。

∂/∂＋∂ρUk/∂x－∂/∂x∙[(＋σμt)∙∂/∂x]＝τ∂U/∂x－*（6）

∂/∂＋∂ρUω/∂x－∂/∂x∙[(＋σμt)∙∂/∂x]＝γ/t∙τ∙∂U/∂x－*∙2＋2(1－2)∙σ2/∙∂/∂x∙∂/∂x（7）

为湍流动能，为湍流动能的特定消散，τ为雷诺应力，它们分别定义为

＝1/2 uu（8）

/*（9）

τ＝t(∂U/∂x＋∂U/∂x)－2/3∙δ（10）

为湍流动能消散率，可由式（11）求得；δ为克罗内克函数，t＝t/为动力涡黏性，其中t可通过涡流黏度公式（12）得到。

＝t∙∂u/∂x∙∂u/∂x（11）

t＝/∙1/max(1/*,2/1ω) （12）

x表示笛卡尔坐标，表示应变率大小，*表示湍流阻尼黏度系数，2为混合函数，由式（13）求得。

2＝tanh(22) （13）

2＝max(2∙1/2/0.09, 500/(2) （14）

是节点到最近壁面的距离，2是关于节点到最近壁面距离的函数，σ、σ、、σ2、*为模型系数

2.2 离散相方程

在离散相模型中，粒子的运动行为是由力平衡方程计算的。根据牛顿第二定律，建立单颗粒运动方程如式（15）所示。

dD/d＝CDdrag∙(C－D)＋∙(D－C)/D（15）

CDdrag为单颗粒曳力函数，用于确定离散相和连续相的相互作用关系，该值可由式（16）求得，C和D分别为连续相和离散相速度。

CDdrag＝Σ[3drag∙C/(4D∙D)(C－D)2′D∙Δ（16）

drag作为阻力系数，可由阻力系数定律确定，′D为离散相质量流量

drag＝1＋2/eD＋3/eD2（17）

1、2、3为常数，与粒子雷诺数相关；eD为离散相雷诺数，计算公示如式（18）所示，D为离散相粒子直径。

eD＝C(D－C)D/C（18）

3 方法与参数设定

3.1 材料与仪器设备

金银花药材，河北省安国市腾跃药业有限公司，批号211010，经天津中医药大学中药学院张丽娟教授鉴定为忍冬科忍冬属植物忍冬Thunb.的干燥花蕾或带初开的花。药材通过冷凝回流方式进行提取，通过H-spray 5S先导式喷雾干燥设备生产得到干燥颗粒，用作旋风分离器的注入粒子进行流场模拟试验。

H-spray 5S先导式喷雾干燥设备、H-spray 5S型旋风分离器，天津市现代创新中药科技有限公司；DH-300固体密度仪，北京仪特诺电子科技有限公司；Mastersizer-3000激光散射仪，英国Malvern Instruments有限公司。

3.2 金银花提取液干燥颗粒物性参数测定与设备的颗粒得粉率测定

金银花提取液干燥颗粒的粒径分布由Mastersizer-3000激光散射仪测定得到，颗粒的粒径分布在1.88～35.3 μm，且各粒径的颗粒占比在总干燥颗粒中存在较大差异，其中6.72 μm的颗粒占比最多（图2）。金银花提取液干燥颗粒的密度使用DH- 300固体密度仪测定得到，该值为1.55×103kg/m3。实际试验中，由于旋风分离器与喷雾干燥设备相连接，故使用喷雾干燥设备物料的出口条件作为旋风分离器物料的入口初始条件。经实验检测得到喷雾干燥设备出口的固体颗粒质量流量即为旋风分离器入口的固体颗粒质量流量，该值为94.2 mg/s。

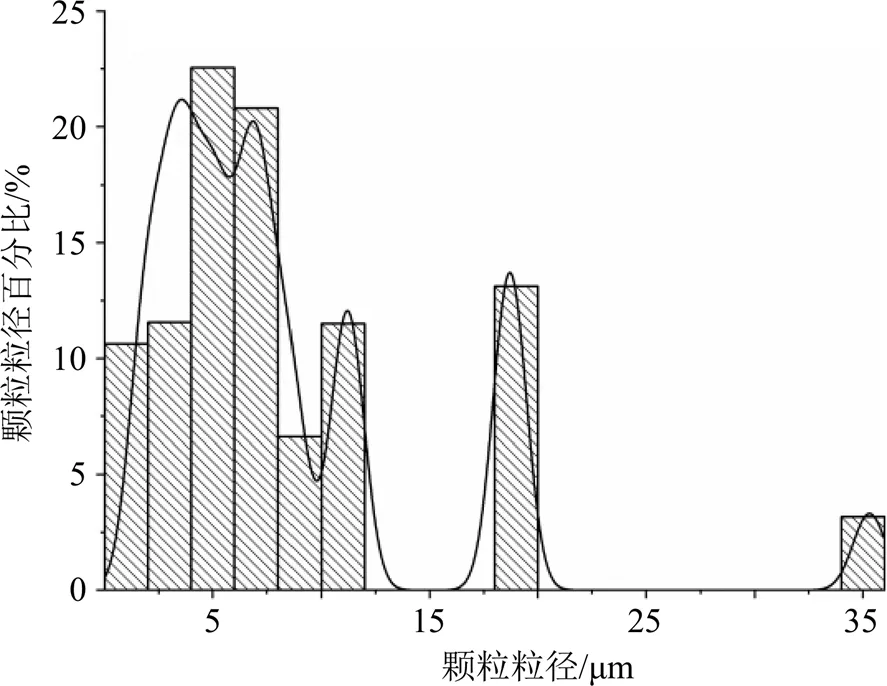
图2 金银花颗粒粒径分布

为了试验测定设备的颗粒得粉率，在长径比∶为3∶1的旋风分离器设备的排灰口底部加装集尘袋，用于捕集分离完成的中药颗粒。通过前期实验研究得到喷雾干燥塔的出口颗粒质量，该值即为注入旋风分离器的颗粒初始量。由式（19）计算得到该条件下旋风分离器的颗粒得粉率。

＝s/0（19）

为设备的颗粒得粉率，s为集尘袋中颗粒质量（kg），0为注入设备的颗粒质量（kg）

3.3 模型边界条件的设定

在模型的计算过程中，连续相选用20 ℃下的空气，密度为1.23 kg/m3，黏度为1.79×10−5kg/(m·s)，空气入口速度由旋风分离器入口的流速检测装置给出，该值为7.73 m/s。研究为了确定最佳的颗粒质量流量设置，基于试验测定值，分别增大15.00%、30.00%的进料质量流量，以及减小15.00%、30.00%的进料质量流量。

在旋风分离器的进气入口处，除了颗粒的质量流量这一重要参数外，入口进气雷诺数也是影响着设备的颗粒得粉率，可以作为颗粒运动状态描述的重要工艺参数。设备的入口进气雷诺数可由式（20）计算得到。

e＝v∙v∙/（20）

e表示入口进气雷诺数，v表示空气密度，v表示空气进气速度，表示进气管道的直径，为空气黏度

由式（20）计算得到旋风分离器入口进气雷诺数为2.49×104，为了进一步明确进气雷诺数对旋风分离器的颗粒得粉率的影响，基于试验值分别增大15.00%的入口进气雷诺数，增大30.00%的入口进气雷诺数，减小15.00%的入口进气雷诺数，减小30.00%的入口进气雷诺数。并设置入口湍流强度为10.00%，水力直径为47.00 mm。

3.4 正交试验筛选分离工艺

采用L25(53)正交试验设计方法，选择入口进气雷诺数、设备长径比、颗粒进料质量流量3个因素。以金银花颗粒分离试验测得数据为基础指标，如“2.2”项所述，扩大参数范围进行最佳工艺筛选，因素水平见表2。

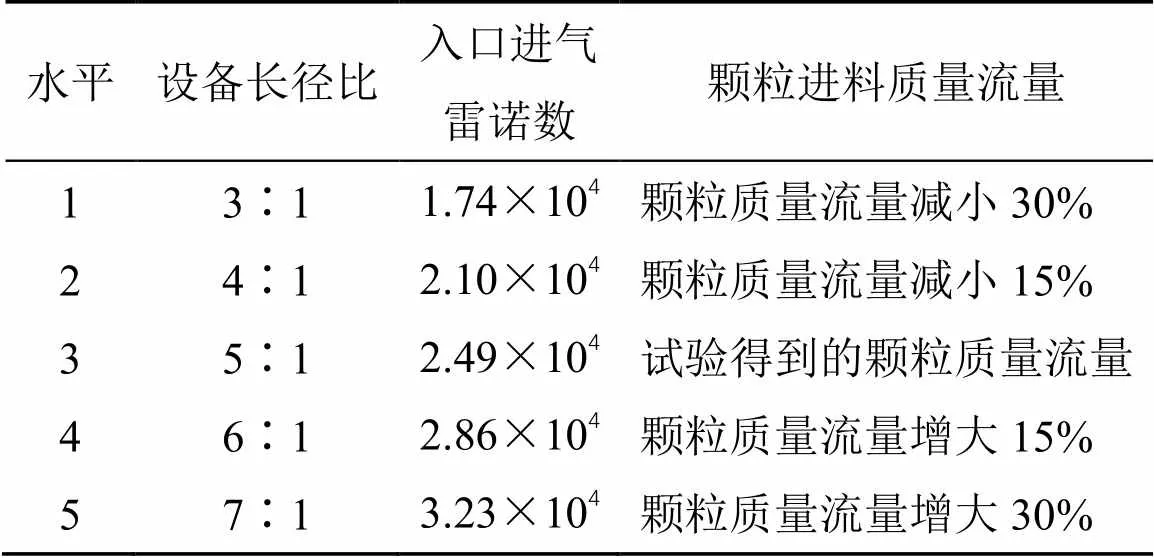
表2 正交试验因素水平

4 流场数值模拟结果及分析

4.1 模型验证

在旋风分离器运行使用过程中，设备的颗粒得粉率是一个最常用的评价指标，为了验证数学模型的准确可靠性，研究对比了设备长径比（∶）为3∶1，入口进气雷诺数为2.49×104，颗粒质量流量为94.2 mg/s时，颗粒得粉率的模拟结果和试验结果。试验在相同初始条件下，平行完成了3次，结果得到设备的平均颗粒得粉率为87.86%，与对应条件下模拟仿真得到的设备的颗粒得粉率89.92%相比，相对偏差为2.34%。结果表明，模拟所采用的模型可准确反映实际设备生产情况，所以运用该模型可以对不同长径比、不同进气雷诺数和不同进料质量流量下旋风分离器的颗粒得粉率情况进行模拟研究。

4.2 气相流场计算结果

图3-a～e分别给出了由模型计算得到的分离器内的旋转速度矢量图。由于同一长径比下的旋风分离器内部旋转速度矢量图差异很小，所以在图3中仅展示了正交试验组1（∶＝3∶1），正交实验组6（∶＝4∶1），正交实验组11（∶＝5∶1），正交实验组16（∶＝6∶1），正交实验组21（∶＝7∶1）的速度矢量图。随着设备长径比的变化，为了更直观的分析设备内部气流情况，取排气管底部与分离器罐体相切平面＝−162 mm作为断面，取分离器罐体锥部高度的1/2处位置作为断面（与长径比分别对应为＝−395、−505、−615、−725、−835 mm），取＝0 mm断面作为断面进行气流情况对比。

由图3可以清楚看出，分离器内部气体流动的不对称性，且设备长径比∶取值越小，气体流动越剧烈，流动形成的旋涡越贴近设备轴。此外随着设备长径比∶取值的增大，设备不断加长，排气管底部与分离器罐体交界处气体流速不断加快，气体流动的复杂程度不断加剧[14-15]。

图4、5分别给出了正交试验组在＝−162断面和＝−（分离器罐体锥部高度的1/2）断面的切向速度比较情况。图4中的流速曲线清楚地表征了涡的结构，处于设备轴附近的强制涡和外层的自由涡，在2种涡的交界处，切向速度突变，出现速度峰。图5结果表明，该断面位置的强制涡消失，不再出现速度突变，气体流动速度趋于平缓，且湍流脉动开始向壁面靠近。此外，随着入口处进气雷诺数的增大，设备内部各处的气流速度都出现了相应增大。

图6、7分别给出了正交试验组在＝−162断面和＝−（分离器罐体锥部高度的1/2）断面的轴向速度比较情况。在图6中同样能清楚看出处于设备轴附近的强制涡和外层的自由涡，涡交界处出现轴向速度突变，且强制涡轴向速度显著高于外层的自由涡轴向速度。由图7可知，在分离器罐体锥部高度的1/2处断面位置的强制涡消失，气体流动轴向速度趋于平缓[16]。

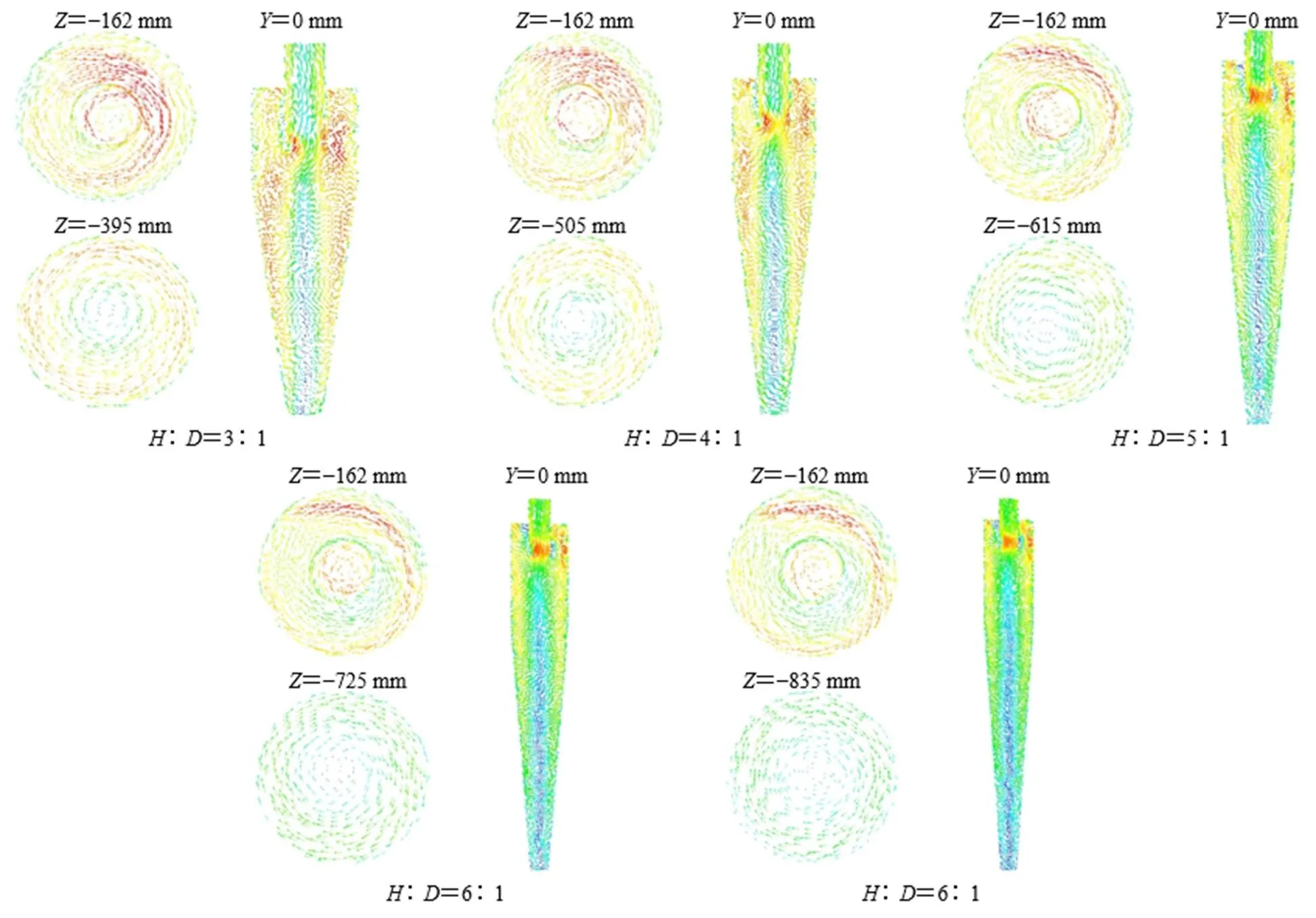
图3 不同设备长径比的分离器内部速度矢量图

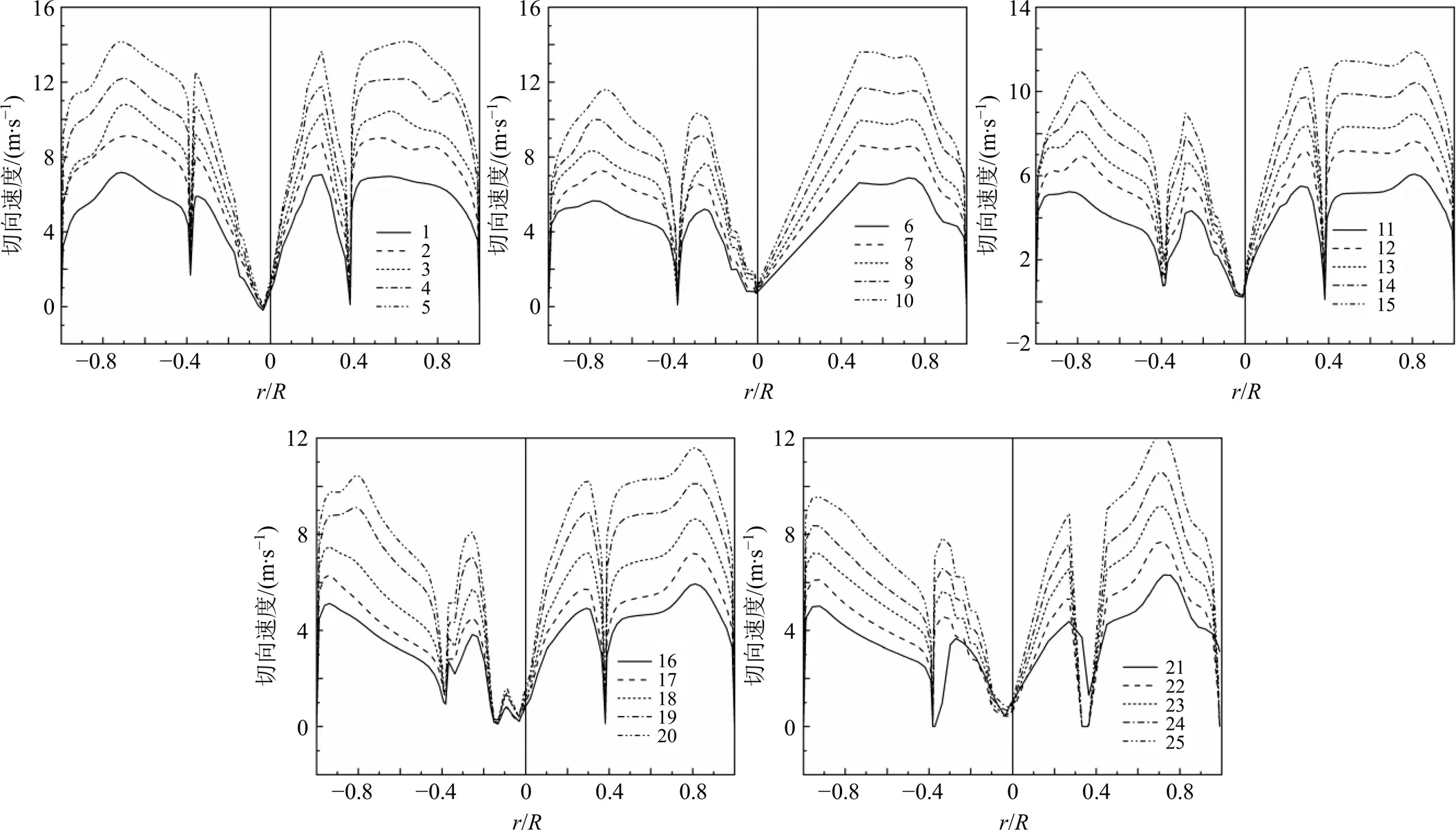
图4 各编号1～25正交试验中分离器(Z＝−162 mm)断面切向速度分布

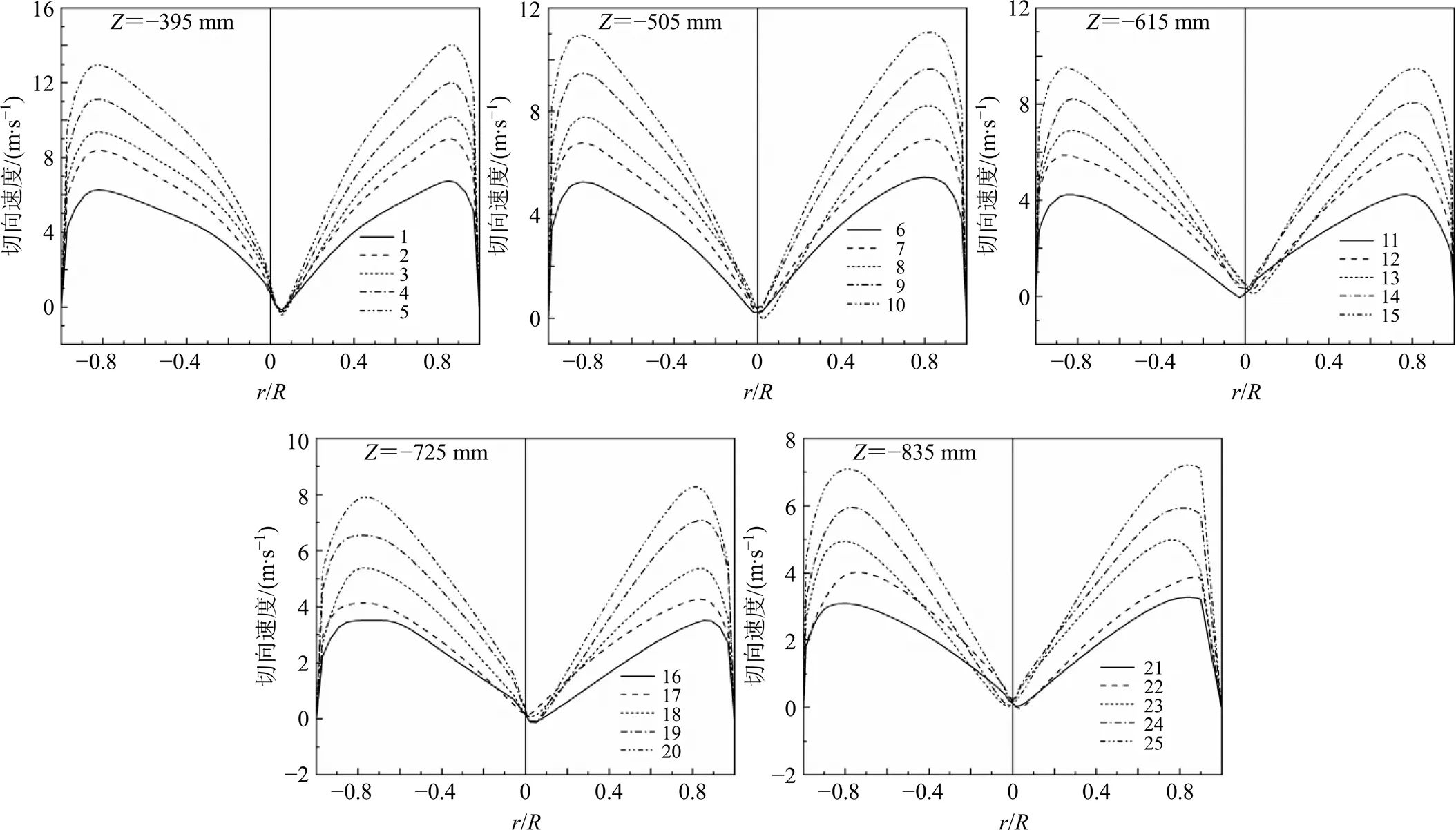
图5 各编号1～25正交试验中分离器圆台罐体不同断面切向速度分布

图8、9分别给出了正交试验组在＝−162断面和＝−（分离器罐体锥部高度的1/2）断面的径向速度比较情况。在图8中速度为负表示气流向设备轴运动。由图9可知，径向速度比切向速度以及轴向速度小，且随着断面分布的不同，利用模型计算得到的径向速度差异明显，说明分离器内部存在沿径向的输运情况。

图6 各编号1～25正交试验中分离器(Z＝−162 mm)断面轴向速度分布

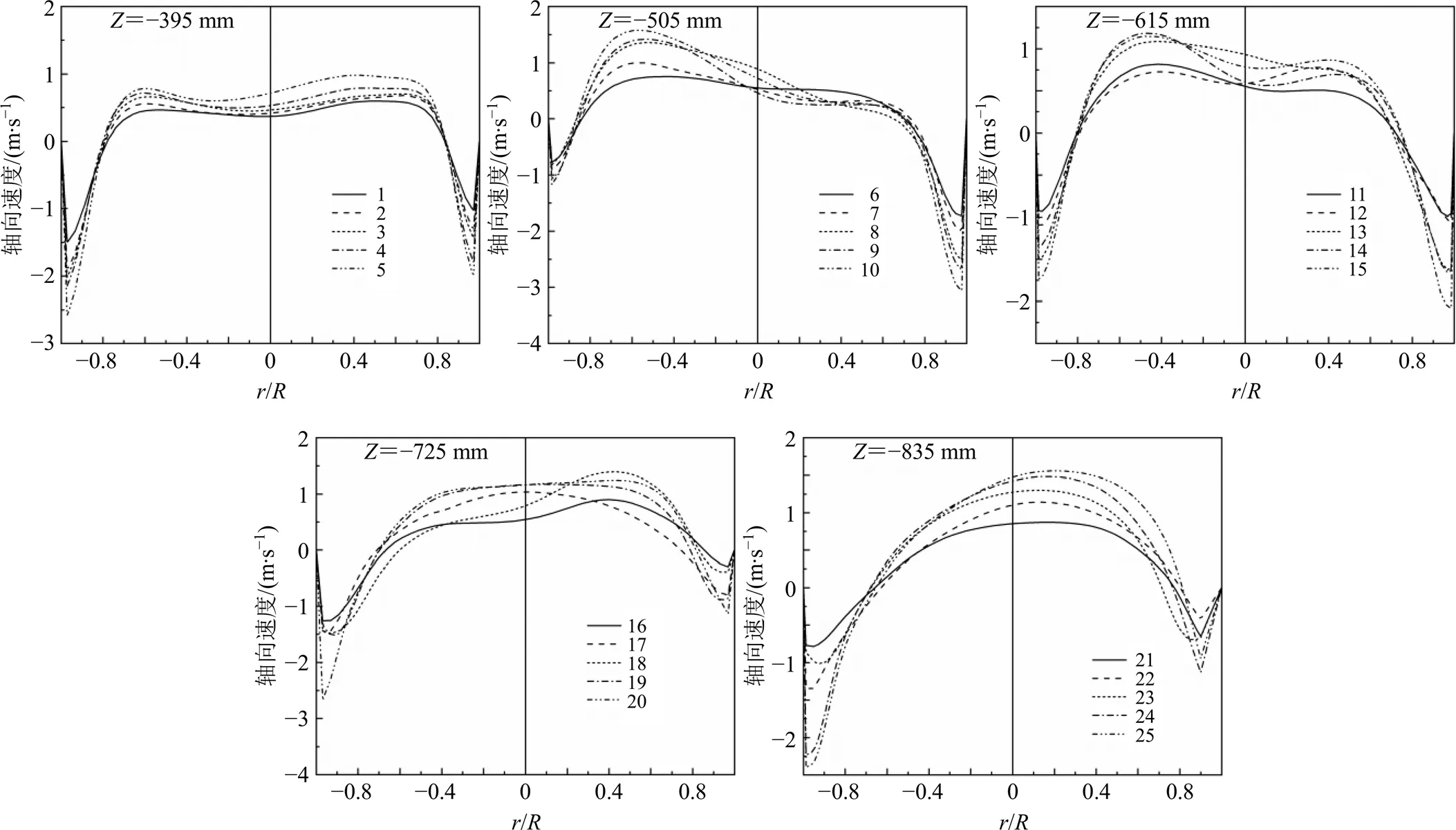
图7 各编号1～25正交试验中分离器圆台罐体不同断面轴向速度分布

综上，在旋风分离器内部的气流存在强制涡和自由涡，涡流带动颗粒在设备内部螺旋运动。随着涡流沿设备轴向运动，气流产生的强制涡逐渐消失，自由涡强度也不断下降，最终让随气流运动的颗粒逐渐沉降，实现颗粒的分离。在实际生产的过程中，由于设备处理的颗粒大小不一，因此有部分颗粒受气流作用明显，将会从排气口逸出设备，从而导致设备的生产效率降低。

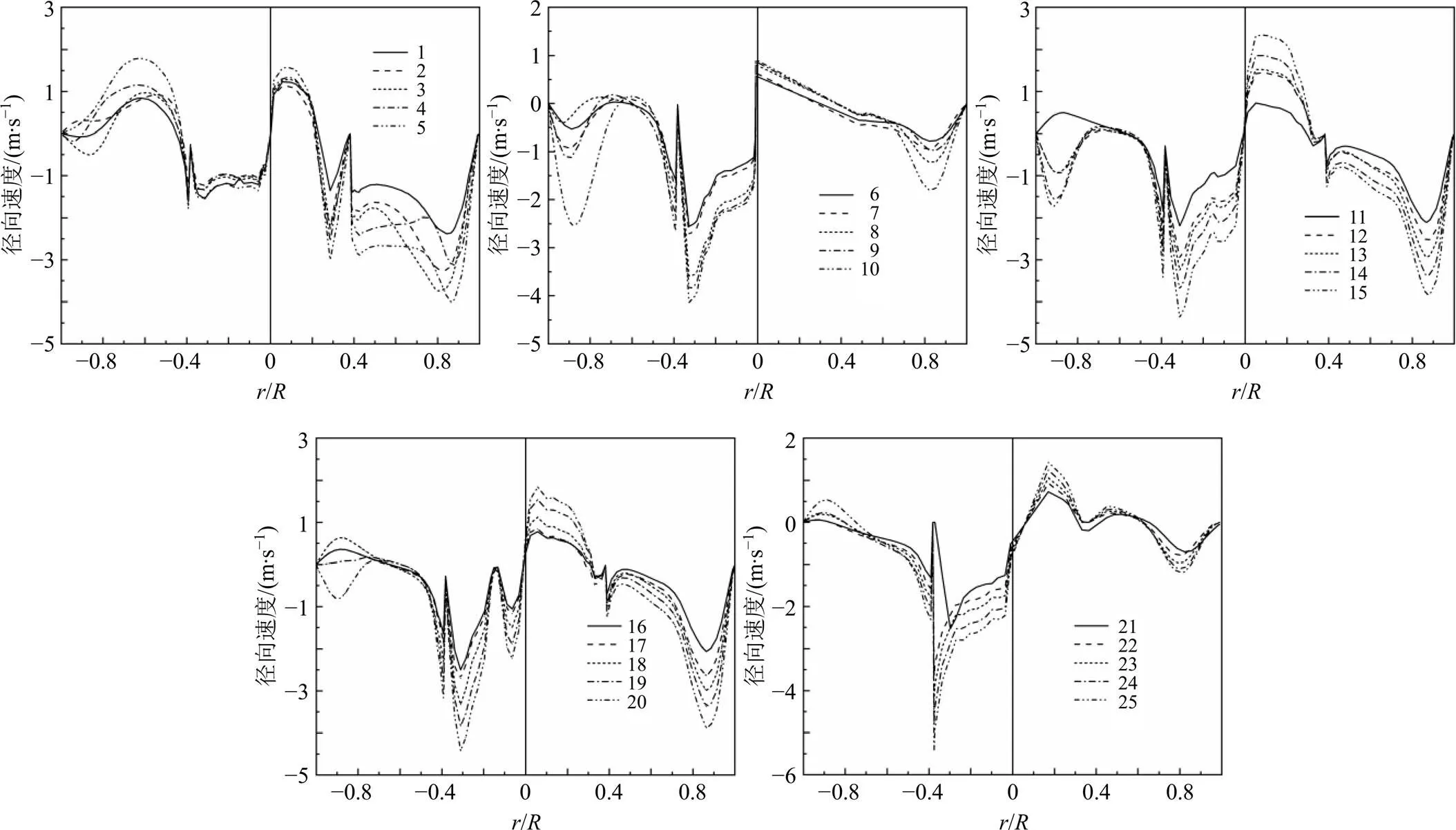
图8 各编号1～25正交试验中分离器(Z＝−162 mm)断面径向速度分布

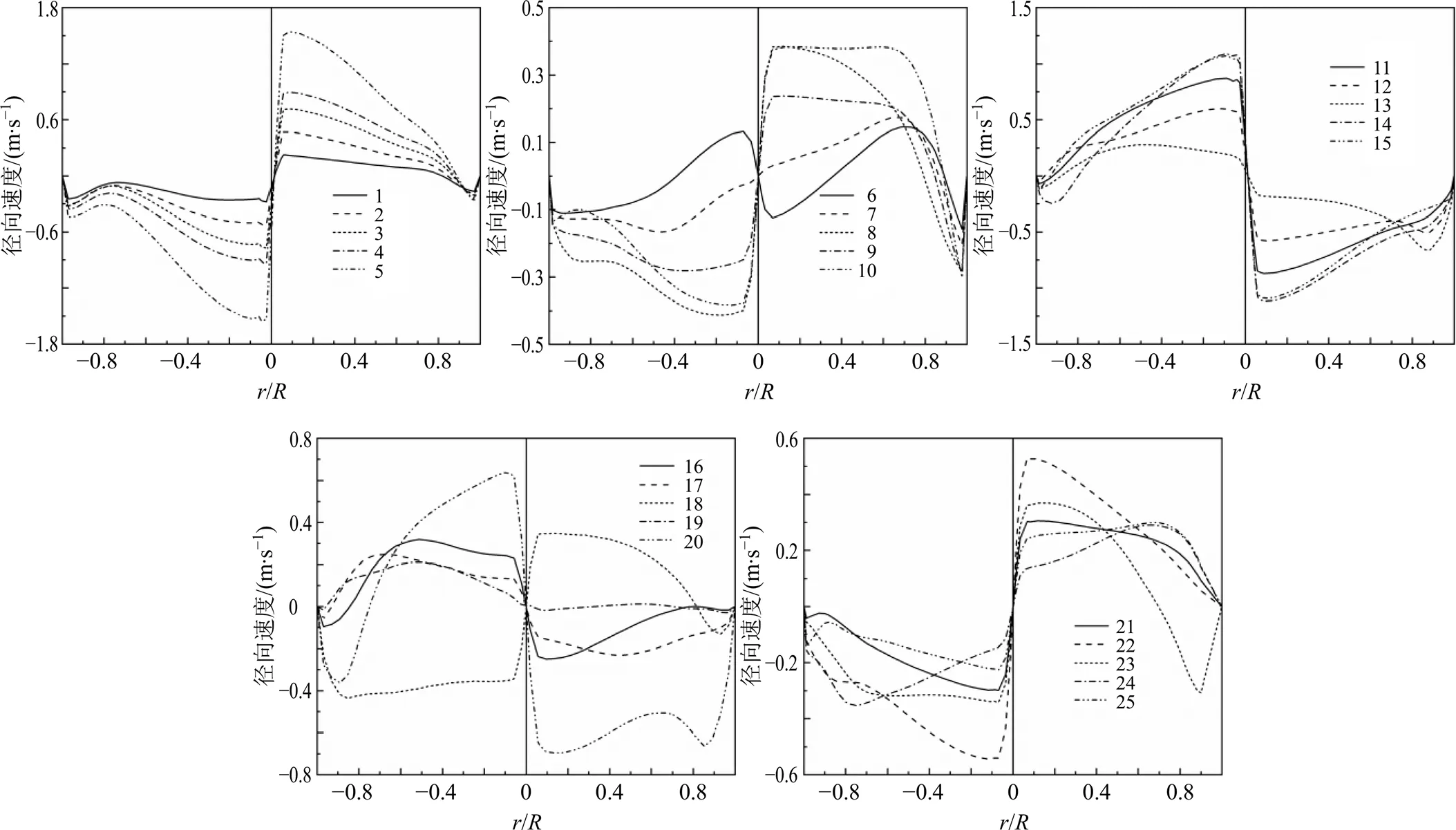
图9 各编号1～25正交试验中分离器圆台罐体不同断面径向速度分布

4.3 颗粒运动模拟

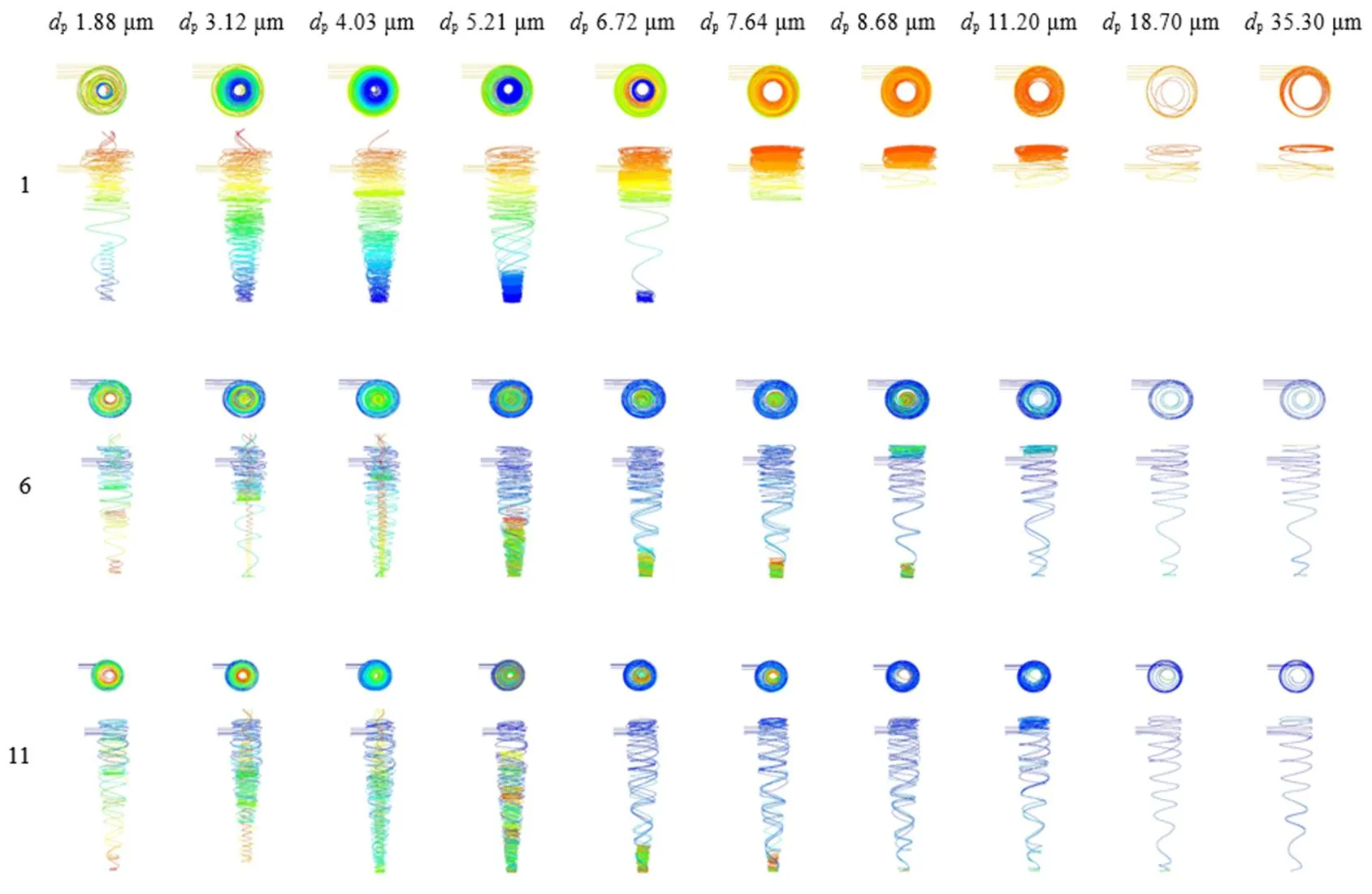
颗粒运动轨迹受设备长径比作用明显，为了更好的说明实验现象，本研究从25组正交实验颗粒轨迹中选择了正交实验编号1（设备∶＝3∶1），编号6（设备∶＝4∶1），编号11（设备∶＝5∶1），编号16（设备∶＝6∶1），编号21（设备∶＝7∶1）的5组运动轨迹图展示在图10中。由图10可知，颗粒粒径（p）为1.88、3.12、4.03 μm的颗粒随气流旋转向下螺旋运动，其中部分颗粒在到达锥部后又随内部的上升气流螺旋向上运动，进入排气管，逸出设备；部分颗粒在没有到达设备底部时就进入内旋流，通过旋流进入排气管。

对于颗粒粒径稍大的颗粒，由于受到较大的离心力作用，被甩向壁面，沿壁面螺旋下滑，到达分离器底部，完成分离[17]。颗粒粒径为7.64～35.30 μm的颗粒在设备内部出现了“上灰环”效应，即颗粒大部分聚集在分离罐体圆柱部分与排气管之间，该现象在设备∶＝3∶1和4∶1的情况下尤为明显，随着设备长径比的增大，该现象逐渐减弱，颗粒随气流向分离器底部螺旋运动。

考虑出现该现象是因为在∶较小的设备内部，气流运行的轴向距离较短，气体的螺旋涡流作用更强（轨迹涡环更加紧密），尤其是排气管附近气流扰动最为剧烈，导致上述粒径范围内的颗粒大量地被束缚在气流中，形成了“上灰环”，随着设备∶的增大，气流运行的涡流作用逐渐减弱（轨迹涡环逐渐稀疏），颗粒被离心力甩向设备壁面后，气流无法再牢牢束缚颗粒，此时颗粒借自由涡流沿壁螺旋运动到达设备排灰口，“上灰环”现象减弱。

4.4 正交试验结果分析

根据正交试验数据处理方法，对表3所示数据分别进行极差分析与方差分析，以获得设备长径比、入口进气雷诺数和颗粒进料质量流量3个因素的影响主次关系，并对各因素的测量结果影响的显著性做出评价[18-20]。

使用极差分析法对正交试验结果进行分析，该方法中极差等于每种试验因素同一水平平均值中的最大值和最小值之差，颗粒得粉率极差分析数值如表4所示。分析表4数据可知，旋风分离器各影响因素对颗粒得粉率的影响敏感度排序为入口进气雷诺数＞设备长径比＞颗粒进料质量流量，说明对颗粒得粉率影响起主导作用的试验因素为入口进气雷诺数，且随着入口进气雷诺数的增大，颗粒得粉率增加，呈正相关，其中颗粒进料质量流量对颗粒得粉率影响最小。

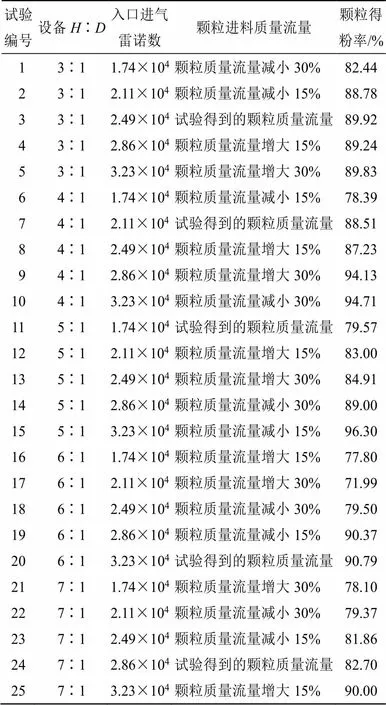
表3 金银花颗粒得粉率正交试验结果

表4 金银花颗粒得粉率极差分析

为了进一步明确颗粒得粉率和各个试验因素之间的相关关系，对试验结果进行方差分析，如表5所示。可知，设备长径比、入口进气雷诺数、进料颗粒质量流量的因子显著性分别为0.04、0.00、0.66，表明不同的设备长径比和不同的进气雷诺数对颗粒得粉率影响的差异显著，而不同颗粒进料质量流量对颗粒得粉率的影响无显著差异。

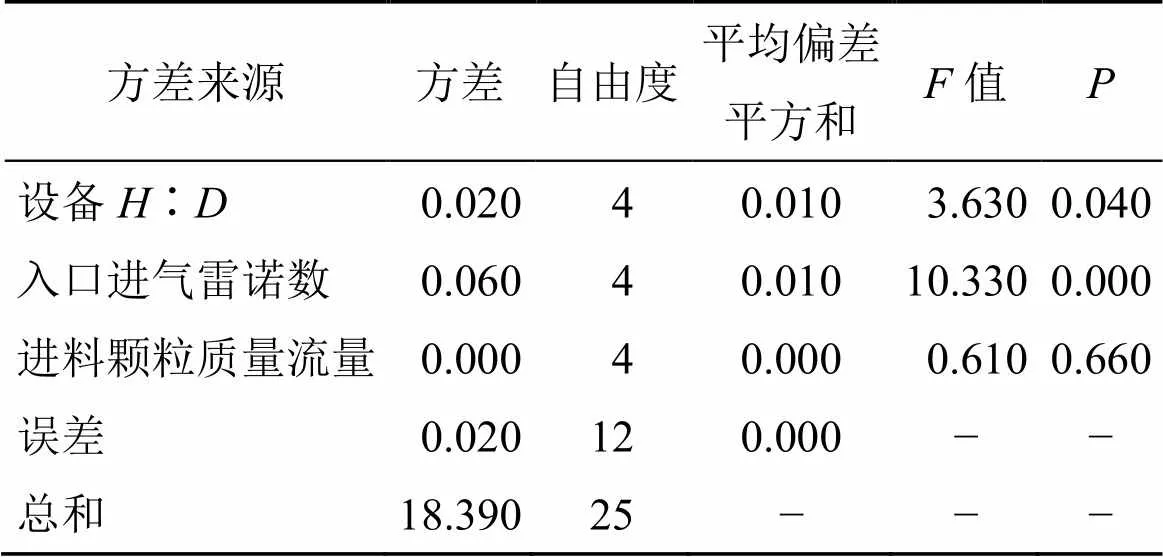
表5 方差分析

综上，在设计旋风分离器过程中为了保证设备生产效率，应重点考察设备入口进气雷诺数，再考虑设备的长径比，而颗粒进料质量流量对生产效率的影响作用较弱，可最后参考调节。本研究通过正交试验设计计算出的最佳工艺为设备∶5∶1，入口进气雷诺数3.23×104，颗粒质量流量减小15%（80.1 mg/s），得到的金银花颗粒得粉率为96.30%。

5 结论

研究以设备的颗粒得粉率为评价指标，采用Shear-Stress Transport（SST）-数值模拟模型，对粉体在设备内部的运动行为过程进行了模拟分析。结果表明，粒径在1.88～4.03 μm的颗粒容易随气体涡流到达设备锥部之后，又借由上升螺旋气流逸出设备；对于粒径稍大的颗粒，由于受到较大的离心力作用，被甩向壁面，沿壁面螺旋下滑，到达分离器底部，完成分离；粒径在7.64～35.30 μm的颗粒在旋风分离器内部易出现“上灰环”现象，该现象随着设备∶的增大会逐渐减弱。

在流场计算的基础上，本研究模拟了受不同设备∶、入口进气雷诺数、颗粒质量流量3个因素影响的金银花颗粒在分离器内的运动规律，计算得到了模拟条件下设备的颗粒得粉率，研究推荐最佳工艺为设备∶＝5∶1，入口进气雷诺数3.23×104，颗粒质量流量80.1 mg/s，得到的金银花颗粒得粉率为96.30%。其中，设备长径比对于颗粒运动轨迹作用明显，设备长径比越大，设备受到的涡流作用越弱，颗粒越容易因挣脱自由涡流作用而完成沉降。而入口进气雷诺数与颗粒得粉率呈正相关，随着入口进气雷诺数的增加，颗粒受到的离心力也在增加，设备内部涡流作用越显著，颗粒越容易在设备内部随涡流运动直至沉降后被捕集。在研究中，大部分颗粒的运动轨迹与空气涡流作用的强弱有关，该现象导致颗粒自身的质量流量对颗粒得粉率的影响与入口进气雷诺数相关。对于旋风分离器的颗粒得粉率而言，是上述3个重要参数综合作用的结果。通过金银花颗粒在旋风分离器中的流场数值模拟研究，为旋风分离器的设备改进和操作工艺优化提供了参考，为其他中药颗粒的分离过程研究提供了借鉴。

利益冲突 所有作者均声明不存在利益冲突

[1] 黄迪菲. 中药制药工艺优化与发展 [J]. 当代化工研究, 2022(012): 137-139.

[2] 薛启隆, 王鐾璇, 苗坤宏, 等. 中药制药工艺知识库构建方法研究 [J]. 中国中药杂志, 2022, 47(12): 3402-3408.

[3] Gao Z, Wang J, Wang J,. Time-frequency analysis of the vortex motion in a cylindrical cyclone separator [J]., 2019, 373: 1120-1131.

[4] 张海红. 旋风分离器流场与分离性能的数值模拟研究 [D]. 郑州: 郑州大学, 2004.

[5] Baltrėnas P, Crivellini A, Leonavičienė T,. Investigation on particulate matter and gas motion processes in the advanced multi-channel cyclone-separator with secondary gas inlets [J]., 2022, 27(1): 1-13.

[6] Winfield D, Cross M, Croft N,. Performance comparison of a single and triple tangential inlet gas separation cyclone: A CFD Study [J]., 2013, 235: 520-531.

[7] 付烜, 孙国刚, 刘佳, 等. 旋风分离器进口涡旋感生速度场的减阻增效作用 [J]. 化工学报, 2011, 62(7): 1927-1932.

[8] 高助威, 王娟, 王江云, 等. 大长径比直筒型旋风分离器内部流动特性研究 [J]. 高校化学工程学报, 2018, 32(6): 1288-1298.

[9] 彭丽, 石战胜, 董方. 基于CFD-DPM的旋风分离器结构优化 [J]. 发电技术, 2021, 42(3): 343-349.

[10] 魏新利, 张海红, 王定标, 等. 旋风分离器内颗粒轨迹的数值模拟 [J]. 郑州大学学报: 工学版, 2004(3): 14-17.

[11] Menter F R. Two-equation eddy-viscosity turbulence models for engineering applications [J]., 1994, 32(8): 1598-1605.

[12] Loureiro J B R, Alho A T P, Freire A P. The numerical computation of near-wall turbulent flow over a steep hill [J]., 2008, 96(5): 540-561.

[13] El-Behery S M, Hamed M H. A comparative study of turbulence models performance for separating flow in a planar asymmetric diffuser [J]., 2011, 44(1): 248-257.

[14] 闫思博, 单学军, 刘芳芳. 旋风分离器分离效率影响因素分析 [J]. 水泥工程, 2022(4): 12-16.

[15] 焦丹丹, 李大尉, 郑辉, 等. 基于分离器工作参数优化及性能分析 [J]. 自动化技术与应用, 2022, 41(8): 113- 114.

[16] 曹万秋. 旋风分离器气相流场数值模拟分析 [J]. 轻金属, 2022(005): 59-62.

[17] 杨柳松, 刘云峰, 孙潞潞, 等. 旋风分离器分离效率关键影响因素研究 [J]. 矿山机械, 2022, 50(2): 44-49.

[18] 赵庆磊, 王以宪. 基于SPSS的正交试验在铁矿石检测中应用研究 [J]. 中国检验检测, 2021, 29(1): 26-27.

[19] 张冬梅, 王灿, 张垒垒, 等. 基于正交设计试验方法的螺栓拧紧伸长量影响因素研究 [J]. 工程机械, 2020, 51(3): 39-43.

[20] 王君顺. 基于正交设计的弱膨胀性泥岩相似材料配比试验研究 [J]. 甘肃科学学报, 2022, 34(4): 130-136.

Numerical simulation ofparticles in cyclone separator

MIAO Kun-hong1, 2, 3, CUI Peng-di1, 2, 3, XUE Qi-long1, 2, 3, YU Yang1, 2, 3, LI Zheng1, 2, 3

1. College of Pharmaceutical Engineering of Traditional Chinese Medicine, Tianjin University of Traditional Chinese Medicine, Tianjin 301617, China 2. State Key Laboratory of Component traditional Chinese Medicine, Tianjin 301617, China 3. Haihe Laboratory of Modern Chinese Medicine, Tianjin 301617, China

To investigate the movement behavior ofparticles (LJFP) in the cyclone separator and the changing laws of the movement process of particles in the equipment under different design parameters and operating conditions.Based on the simulation technology, the movement laws of LJFP in the separator affected by the length- diameter ratio of different equipments, the Reynolds number of inlet air and the particle mass flow rate were investigated. The reliability of the model was analyzed with the powder yield of LJFP as the validation index parameter.The particle trajectory distribution under different process conditions through simulation was obtained, and the corresponding powder yield of particles wascalculated. The optimal process recommendations for the separation of LJFP were as follows: The length-diameter ratio of the equipment was 5:1, the Reynolds number of the inlet air was 3.23 × 104, and the mass flow rate of the particles was 80.1 mg/s. The powder yield of particles was 96.30%.This study can provide guidance for the research on LJFP in cyclones separators and improve the deficiencies in the control and design of cyclones separators.

cyclone separator;particles; numerical simulation technology; laws of movement; powder yield of particles

R283.6

A

0253 - 2670(2023)04 - 1087 - 11

10.7501/j.issn.0253-2670.2023.04.008

2022-08-23

国家自然科学基金面上项目（82074276）；国家中医药管理局创新团队与人才培养计划（ZYYCXTD-D-202002）；国家“重大新药创制”科技重大专项（2018ZX09201011）；天津中医药大学研究生科研创新项目（YJSKC-20201025）

苗坤宏，硕士研究生，研究方向为中药制药过程智能控制。Tel: 13987626533 E-mail: 13987626533@163.com

于 洋，助理研究员，研究方向为中药制药工程技术研究与产业转化。E-mail: yuyang@tjutcm.edu.cn

李 正，研究员，研究方向为中药制药工程技术研究与产业转化。E-mail: lizheng@tjutcm.edu.cn

[责任编辑 郑礼胜]