黏滞阻尼器参数对连续梁桥地震响应影响分析

刘朝福，刘维娟，周慧慧

（1.云南省交通规划设计研究院有限公司，云南 昆明 650224；2.云南新创新交通建设股份有限公司，云南 昆明 650000）

0 引言

地震是一种常见自然灾害，我国西部较为频发，害给国家和人民造成了严重损失。桥梁作为地震灾害中的控制性工程，发挥着不可替代的动脉运输作用，既能第一时间进行抢险救灾、运输物资，又能在灾后重建中承担大部分运输任务，是地震灾害发生时最重要的运输渠道。近些年来，连续梁桥在地震作用中的可靠性及性能得到了系统且深入的研究[1]。其中，减隔震技术[2]可以提高桥梁可靠性与抗震性能。目前在桥梁结构中设置阻尼器被认为是经济、合理的减隔震方法之一。且阻尼器加工方便、施工简单、安全性好，减震效果明显，对环境无副作用，得到了社会上专家、学者的广泛认可，有着广阔的发展前景。

1 工程背景

本文以昆明附近5 跨20 m 的连续梁桥为工程背景，上部结构为连续T 梁[3-4]；0 号桥台、5 号桥台采用双柱埋置式桥台，桥墩采用柱式墩，桥面宽12 m，上设10 cm 厚C50 现浇桥面混凝土，10 cm 沥青混凝土桥面铺装，全桥桥型布置如图1 所示。

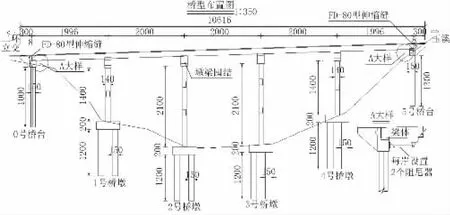
图1 桥梁设计简图（单位：cm）

2 黏滞阻尼器技术参数

本文桥梁采用的是孔隙式黏滞阻尼器。黏滞阻尼器[5-7]装置的动力核心是一套液压装置系统，并辅助活塞头、活塞杆、油缸和黏性阻尼液体。

阻尼力主要来源于以下两个方面：孔缩效应产生的阻尼力和流体黏滞摩擦产生的阻尼力。流速分布示意图如图2 所示。由于篇幅有限，不再具体推导。

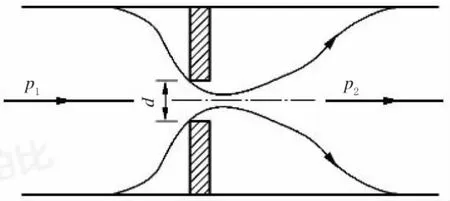
图2 孔缩效应流动示意图

孔缩效应产生的阻尼力

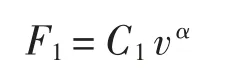
黏滞摩擦产生的阻尼力

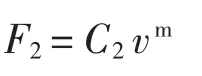
式中：C 为阻尼系数；v 为活塞的运动速度；α 为阻尼指数，p1、p2为流束两侧压强；d 为活塞杆直径；m 为黏度衰减指数。

孔隙黏滞阻尼器阻尼力

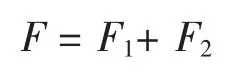
本文着重研究孔缩效应产生的阻尼力F1技术参数变化对桥梁结构的影响。黏滞摩擦产生的阻尼力F2不再赘述。

3 结构建模

3.1 荷载取值

（1）汽车荷载：公路—Ⅰ级。

（2）温度荷载：考虑了结构整体升温25℃,整体降温25℃，温度梯度按规范取值。

（3）地震荷载：震动峰值加速度为0.2g，地震基本烈度为Ⅷ度。

3.2 基础及边界条件的模拟

基础在建模的过程中，考虑桩-土的共同作用，用等效的土弹簧来进行模拟。桥墩与盖梁、承台的连接，在Midas Civil 中应用刚性连接来模拟。桥墩墩顶节点从属于盖梁底节点，桥墩墩底节点从属于承台顶节点。桩基与承台的连接同样采用刚性连接来模拟，桩顶的节点从属于承台底节点，桩底采用固结。两侧桥台设置滑动支座，1#、3#、4# 桥墩设置板式橡胶支座，2#桥墩采用墩梁固结。桥梁二期荷载转换为质量来模拟二期铺装。

3.3 地震波的模拟

采用动力时程分析方法对桥梁进行抗震计算分析。根据《城市桥梁抗震设计规范》[8]5.3 条规定，选取Elcent 波、Sanfer 波和sanfern 波3 条地震波对结构进行动力时程分析。建立的有限元模型如图3 所示。

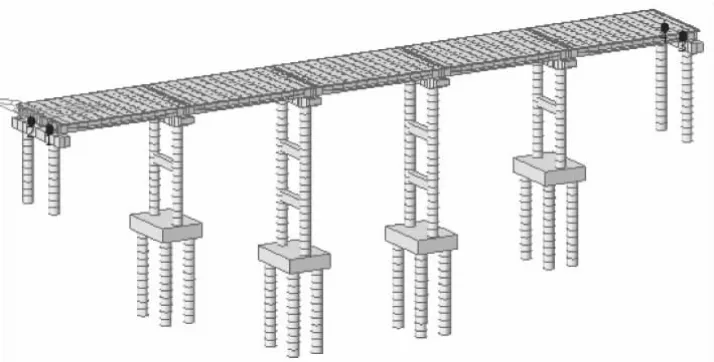
图3 有限元模型图

4 黏滞阻尼器对连续梁桥抗震性能影响分析

根据相关文献可知，计算黏滞阻尼器恢复力的模型为：

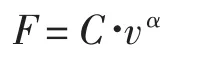
式中阻尼器的阻尼系数C 和阻尼指数α 这两个重要的参数决定了黏滞阻尼器的性能，也是黏滞阻尼器桥梁在地震响应下分析的重要参数。因此，研究这两个参数对桥梁的影响并与普通的桥梁结构在地震响应下的性能进行对比，可为黏滞阻尼器的参数设计提供依据。

图4 是分析模型在阻尼系数C=4 000、阻尼指数α=0.4 工况下前6 阶阵型及相应震动周期（括号内数值为未设置阻尼器工况下桥梁阵型及周期）。

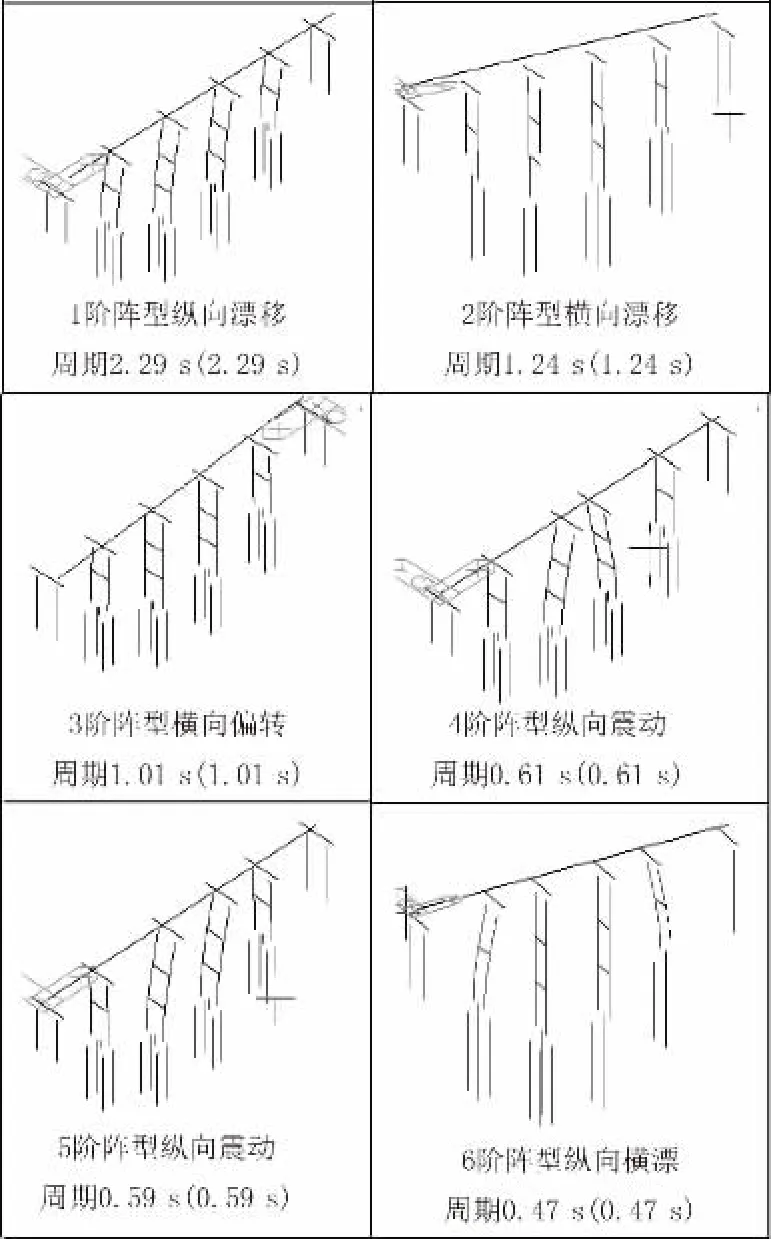
图4 桥梁阵型及周期

通过对阵型及周期的分析可知，阻尼器的设置不会改变结构的固有震动周期。阻尼器对结构只提供附加阻尼，而不提供附加刚度，因而不会改变结构的自振周期。

本文模型中2# 墩采用墩梁固结，其承担的地震荷载较活动墩大，其余活动墩墩顶的位移又相对较大，超出了支座的极限位移。为提高本桥在地震响应下的抗震性能，先通过Midas Civil 在0#、5# 桥台分别模拟设置2 套黏滞阻尼器装置。根据以往的研究报告，本文对参数选取的分析工况见表1。

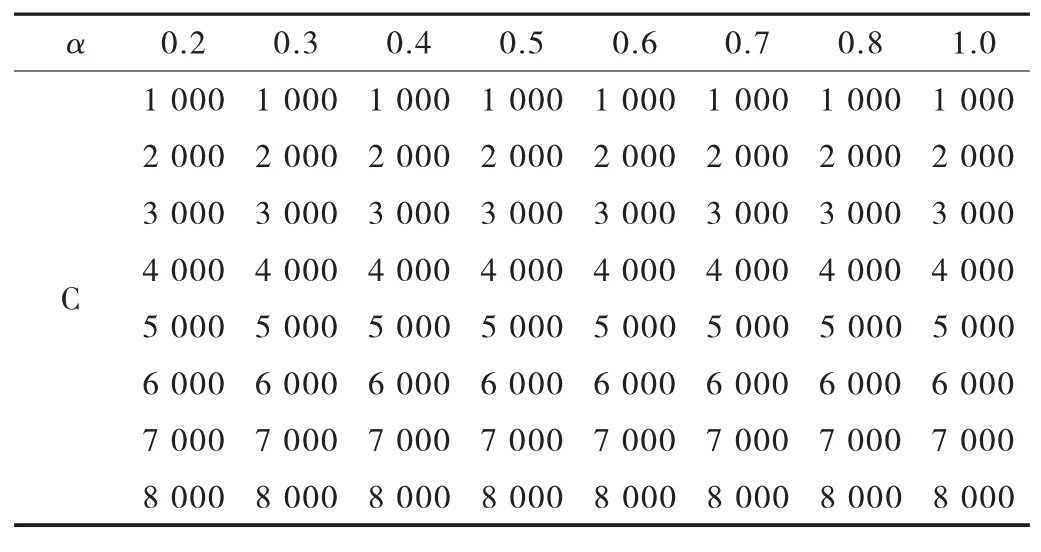
表1 阻尼参数 单位：kN/（m·s -1）

4.1 阻尼系数C 对墩底弯矩的影响

当结构中设置黏滞阻尼器后，在不同阻尼系数下，桥梁的2# 固定墩的墩底弯矩有显著的减少。当α=0.4、C=4 000时，2# 固定墩在EI 波的作用下地震响应最小，为1 567.9 kN·m，如图5 所示。

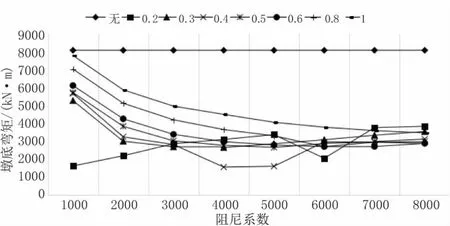
图5 2# 固定墩墩底弯矩

当桥梁设置黏滞阻尼器后，3# 活动墩的墩底弯矩随着阻尼系数的不同而呈现不同的变化。整体而言，当α 取0.2、0.3 或者0.5～0.8时，随着阻尼系数C的增大，墩底的弯矩先增加后趋于稳定，并且相对于不设置阻尼器而言，其活动墩的墩底弯矩增大。当为线型阻尼器时（即α=1），随着阻尼系数C 的增大，墩底的弯矩没有变化，并且墩底弯矩整体减小。其中当C=5 000、α=0.4时，设置阻尼器后桥梁的3# 活动墩在EI 波的作用下地震响应最小，为5 002.1 kN·m，如图6 所示。

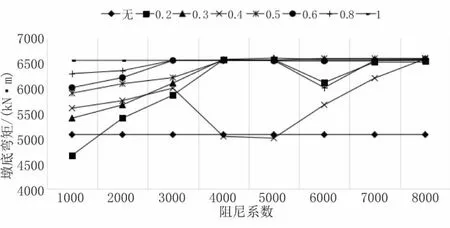
图6 3# 活动墩墩底弯矩

4.2 阻尼系数C 对墩底剪力的影响

当设置阻尼器后，桥梁2# 固定墩的墩底剪力也根据阻尼系数的变化而呈现不同的变化。当采用线性阻尼器时，墩底剪力随着阻尼系数的变化而保持稳定。当α=0.2 或者0.4时，墩底剪力随着阻尼系数的变化而波动，先增大，后降低，再增大。当α=0.3 或者0.5～0.8时，墩底的剪力随着阻尼系数的增大而增大。当α=0.4、C=4 000时，设置阻尼器后桥梁的2#固定墩在EI 波的作用下地震响应最小，为2 689.2 kN，如图7 所示。

当结构设置黏滞阻尼器后，桥梁的3# 墩（活动墩）的墩底剪力的变化情况与图7 中2# 固定墩的变化情况相类似，并且当α=0.4、C=4 000时，设置阻尼器后桥梁的3# 活动墩在EI 波的作用下地震响应最小，为2 699.8 kN，如图8 所示。

图7 2# 固定墩墩底剪力

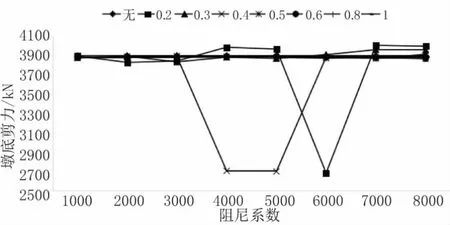
图8 3# 活动墩墩底剪力

4.3 阻尼系数C 对梁端位移的影响

当设置阻尼器后，桥梁的梁端位移得到了显著的改善，大大减小了梁端的位移。其中，当α=0.4、C=4 000时，设置阻尼器后桥梁的梁端位移在EI 波的作用下地震响应最小，为29.9 mm，如图9 所示。

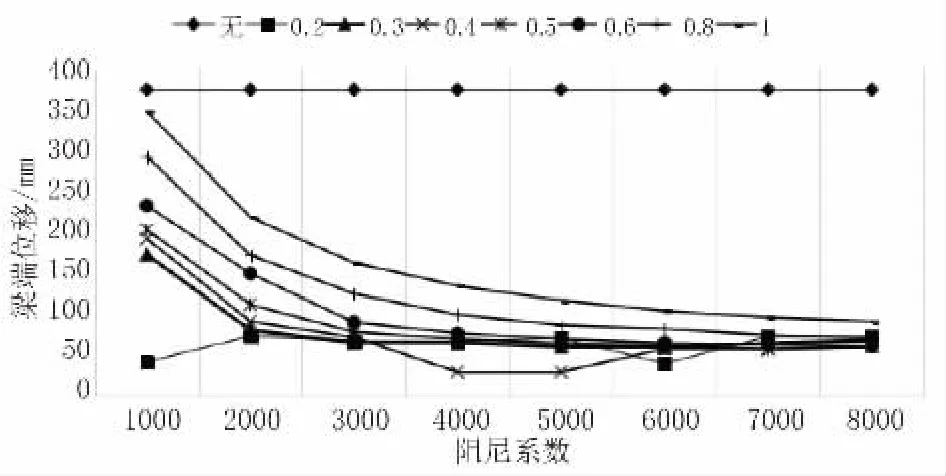
图9 梁端位移

4.4 阻尼指数α 对墩底弯矩的影响

当设置阻尼器后，桥梁的2# 固定墩的墩底弯矩有非常显著的减少。其中，当阻尼系数C=1 000～3 000时，墩底的弯矩随着阻尼指数α 的增加而逐渐增大；但是当阻尼系数C 大于3 000时，墩底的弯矩随着阻尼指数α 的增加而先减小后增大。其中，当α=0.4、C=4 000时，设置阻尼器后桥梁的2#固定墩在EI 波的作用下地震响应最小，为1 567.9 kN·m，如图10所示。

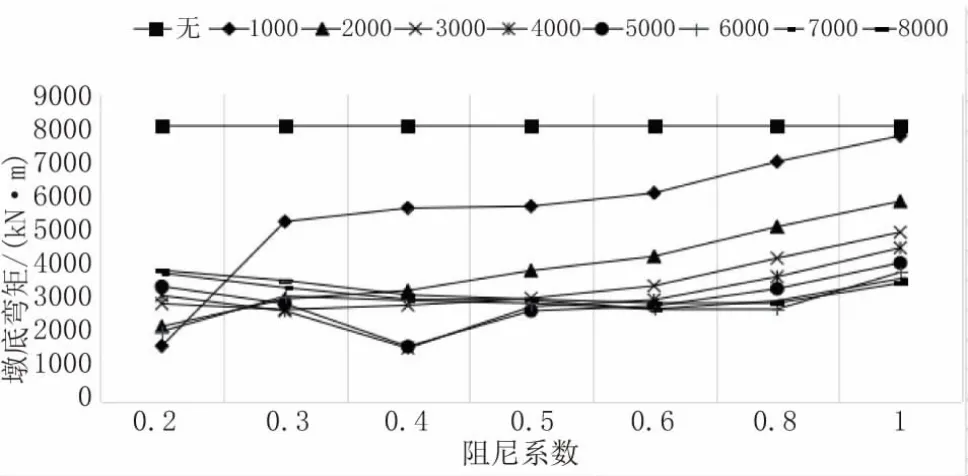
图10 2# 固定墩墩底弯矩

当结构设置黏滞阻尼器后，桥梁的3# 墩（自由墩）的墩底弯矩随着阻尼系数的不同而呈现不同的变化。当为阻尼器的阻尼系数较大（即C=8 000）时，随着阻尼指数α 的增大，自由墩的墩底弯矩并没有很大变化，并且相对于不设置阻尼器的结构而言，墩底弯矩有所增大。当C 在4 000～7 000 之间时，墩底的弯矩随着阻尼指数α 的增大而不断波动，表现为先降低，后增大，再趋于稳定。当C 在1 000～3 000之间时，墩底的弯矩随着阻尼指数的增加而逐渐增大。并且相对于不设置阻尼器的结构体系而言，其活动墩的墩底弯矩反而增大。当C=5 000、α=0.4时，设置阻尼器后桥梁的3# 活动墩在EI 波的作用下地震响应最小，为5 002.1 kN，如图11 所示。

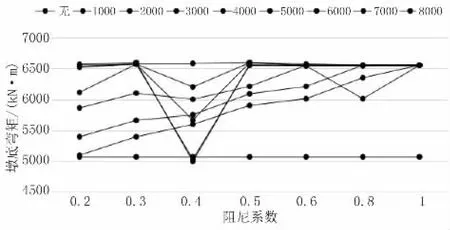
图11 3# 活动墩墩底弯矩

4.5 阻尼指数α 对墩底剪力的影响

当结构设置阻尼器后，桥梁的2# 固定墩的墩底剪力也随着阻尼系数的变化而呈现不同的变化。当黏滞阻尼器的阻尼系数C 大于6 000时，2# 固定墩的墩底剪力随着阻尼指数的增加而先减小后趋于稳定。当阻尼系数C=4 000 或3 000时，墩底剪力随着阻尼指数α 的增加而波动较大，表现为先减小，后增加，再趋于稳定。当阻尼系数C 小于3 000时，随着阻尼指数α 的增加，墩底的剪力保持稳定。当α=0.4、C=4 000时，设置阻尼器后，桥梁的2# 固定墩在EI波的作用下地震响应最小，为2 689.2 kN，如图12所示。

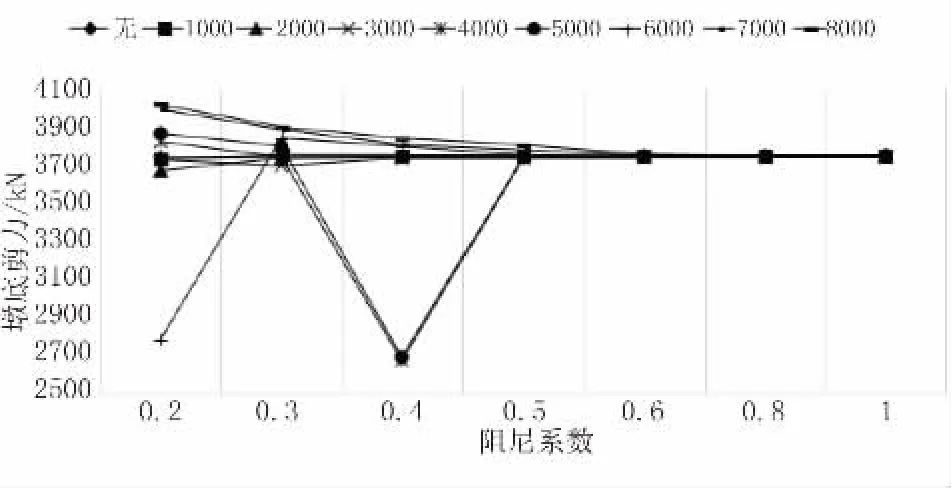
图12 2# 固定墩墩底剪力

当结构设置阻尼器后，桥梁的3# 活动墩的墩底剪力的变化情况与图12 中2# 固定墩的变化情况相类似，并且当α=0.4、C=4 000时，设置阻尼器后，桥梁的3# 活动墩在EI 波的作用下地震响应最小，为2 699.8 kN，如图13 所示。

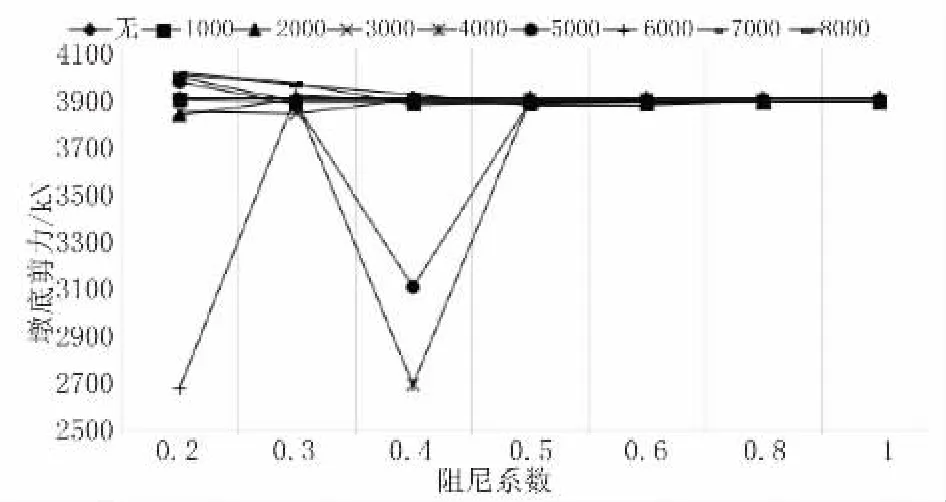
图13 3# 活动墩墩底剪力

4.6 阻尼指数α 对梁端位移的影响

如图14 所示，当结构设置黏滞阻尼器后，桥梁的梁端位移得到了显著的改善。从图中可以得出：当C 在1 000～3 000 之间时，梁端的位移随着阻尼指数α 的增加而逐渐加大。当C=4 000 或者5 000时，梁端的位移随着阻尼指数α 的增大而先减小后增大。当C 不小于6 000时，梁端的位移随着阻尼指数α的变化而趋于稳定。当α=0.4、C=4 000时，设置阻尼器后，桥梁的梁端位移在EI 波的作用下地震响应最小，为29.9 mm。

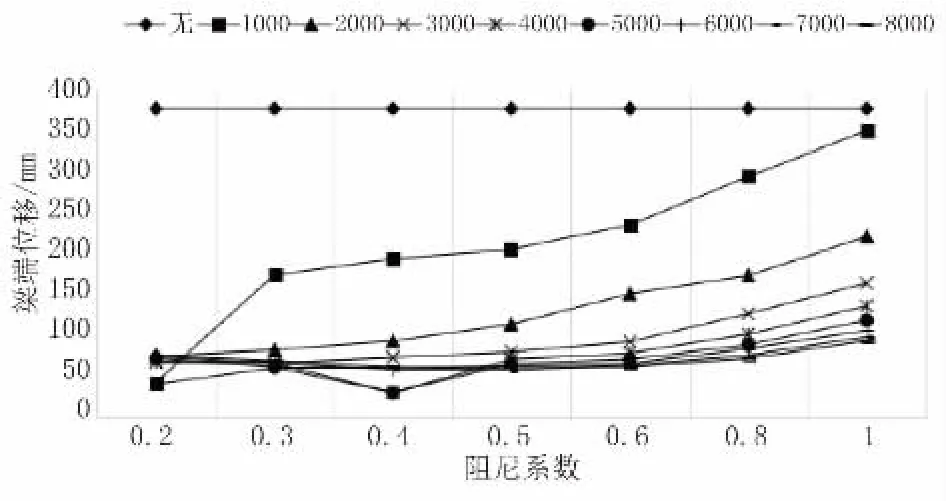
图14 梁端位移

5 结论

本文以实际工程案例为依托，建立了桥梁有限元分析模型。运用非线性动力时程分析法对黏滞阻尼器阻尼系数C、阻尼指数α 进行研究，得出以下主要结论：

（1）当阻尼系数C 一定时，墩底弯矩与梁端位移同阻尼指数呈正向相关关系，随着阻尼指数α 的增大而增大；墩底剪力同阻尼指数呈负向相关关系，随着阻尼指数α 的增大而减小。

（2）当阻尼指数α 一定时，墩底弯矩与梁端位移同阻尼系数C 呈负向相关关系，随着阻尼系数C 的增大而减小；墩底剪力同阻尼系数呈正向相关关系，随着阻尼系数C 的增大而增大。

（3）采用黏滞阻尼器进行桥梁减震设计时，应根据桥梁实际结构的地震响应选择合理的阻尼系数和阻尼指数，阻尼系数并非越大越好，应根据桥梁结构的地震响应情况具体确定。

（4）阻尼器的设置不会改变结构的固有震动周期。阻尼器对桥梁结构只提供附加阻尼，而不提供附加刚度，因而不会改变结构的自振周期。