基于Neuroptica的光学神经网络仿真实验设计

卢 瑾，苏豪宇，王 艳，任宏亮

（浙江工业大学a.计算机科学与技术学院；b.信息工程学院，杭州 310023）

0 引言

光具有天然的并行处理能力以及成熟的波分复用技术，使数据传输容量及带宽大幅度提升。与传统电子器件相比，光学器件具有超大的信号带宽、低延迟和可重构性。

光学神经网络（Optical neural network，ONN）是指经过一定的调制手段以后，将信息加载在光的强度、相位或者偏振等特征上，并通过光的干涉、衍射、偏振或散射等特性直接实现神经网络的计算［1-2］。在计算过程中并不涉及光、电转换的过程，运算结果直接体现在光的输出特性上。光学神经网络能有效减轻软件和电子硬件两者的部分运算，是解决当前算力、功耗极具潜力的途径之一，是人工智能领域很有潜力的研究方向［3-5］。硅光子技术由于其大带宽、低功耗以及和互补金属氧化物半导体（CMOS）工艺兼容性等优势而被认为是突破微电子瓶颈最有希望的候选者之一。根据不同的实现方式，已经提出许多硅光子神经网络体系结构来促进复杂的计算任务，例如衍射神经网络［6-7］和光干涉神经网络［8］。利用衍射元件或光学干涉仪来执行线性操作。已证明硅光子干涉电路比微电子处理器快100 倍，但能量消耗仅为其1／1 000。随着对计算速度和功率的需求迅速增长，硅光子学神经网络为人工智能硬件提供了有前途的替代方案。

Shen等［9］利用硅光学干涉仪芯片实现线性计算，结合电域模拟的非线性激活函数，成功构建全连接神经网络，研制出世界第一颗光子干涉计算单元芯片，通过在这种纳米光子芯片上的深度学习编程实现语音识别功能。Bagherian 等［10］基于光子干涉计算单元芯片，使用时分复用方法扩展了一个可以利用芯片实现图像卷积简单的全连接神经网络。针对用于光子神经网络的反向传播算法很难移植到训练光子神经网络，Hughes等［11］提出片上训练算法。以光子干涉仪计算芯片构建为发端，光计算芯片研究如火如荼进入一个新的阶段［12-13］。不论作为研究还是学习，光子干涉仪芯片作为成熟且即将商用化的光计算芯片都是光子芯片的重要研究基础和对象。

基于片上光电智能计算架构和算法的研究，聚焦光学信号处理和人工智能计算领域的关键问题，采用Neuroptica软件包搭建模型，实现光学神经网络的应用场景拓展，实现用于训练图像处理系统的手写数字数据率（Mixed National Institute of Standards and Technology database，MNIST）手写体数据识别功能，整个实验过程如图1 所示。为设计光子芯片提供重要的研究基础和功能仿真方法；为初学者学习在不同参数下训练模型进行对比实验和自主编程设计ONN 框架实现其它机器学习任务提供重要的仿真平台。

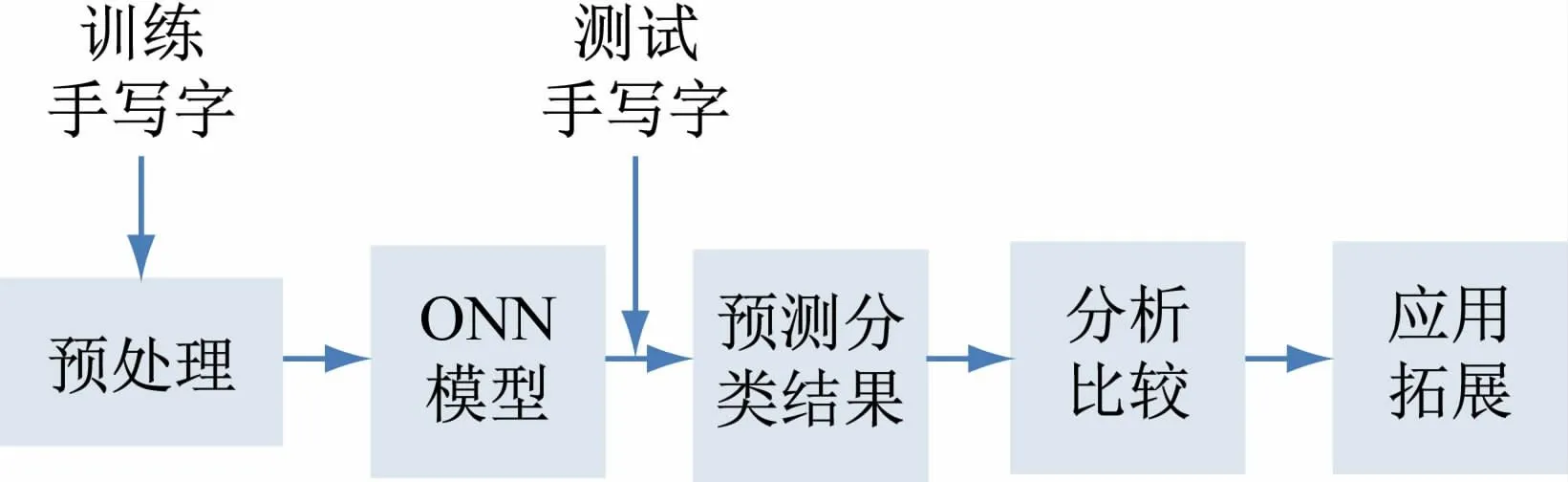
图1 手写体数据识别实验流程图

1 光神经网络理论基础

1.1 光神经网络基本结构

ONN结构如图2 所示，由输入层、输出层以及中间各隐藏层构成。隐藏层包括光学推理单元（Optical Interference Unit，OIU）和光学非线性单元（Optical Nonlinearity Unit，ONU），分别实现光矩阵乘法和非线性激活函数的作用。在ONN的每一层中，信息通过光学矩阵乘法的线性计算组合，应用光学非线性激活函数进行传播。ONN每一层由一个线性矩阵块组成，该矩阵乘以输入向量xin，每层中的fi块为在向量zi上操作的元素非线性激活函数，以产生输出xout。

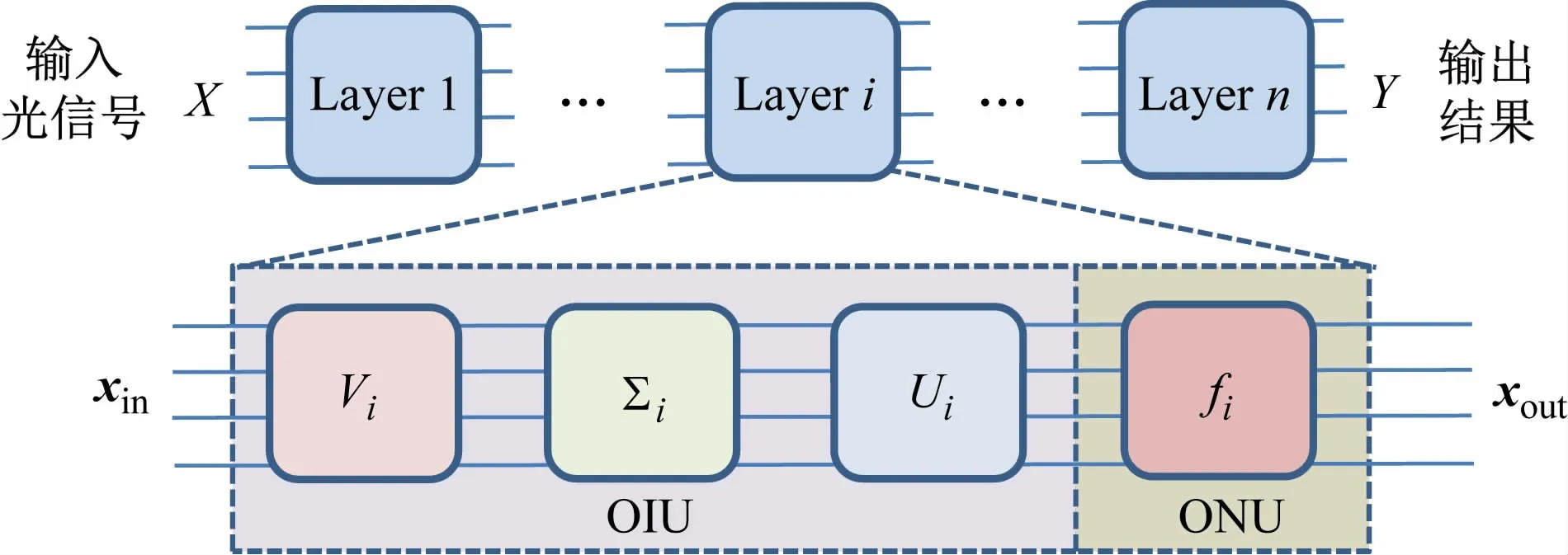
图2 光神经网络基本架构图

1.2 光学推理单元

通过奇异值分解方法（Singular Value Decomposition，SVD），ONN的每层权重实矩阵M 可以分解得到2 个酉矩阵U、V*和一个对角矩阵Σ，则

式中：U 为m×m酉矩阵；Σ 为对角线上非负实数的m×n对角矩阵；V*为n×n酉矩阵V的复共轭。由于任意的酉矩阵都可以表示为一系列旋转矩阵的乘积，如果继续对酉矩阵进行分解，可得

式中，Rθij为单位矩阵。任何一元变换U、V都可用光学分束器和移相器来实现［14］，这样就能使用一系列马赫-曾德尔调制器构建用于一般矩阵乘法的光网络，该方式实现的矩阵乘法原则上不消耗功率，使得ONN架构相比较于ANN具有更高的效率。

OIU在硅光子集成电路中由马赫曾德干涉仪（Mach Zehnder Interferometer，MZI）级联阵列的可编程纳米光子器实现，MZI由前后2 个3 dB 定向耦合器连接上下2 个硅波导分支构成。内移相器通过改变波导折射率控制输出分光比，外移相器控制差分输出、相位延迟。图3 左下为单层前馈神经网络的光学干涉仪网格实现示意图。

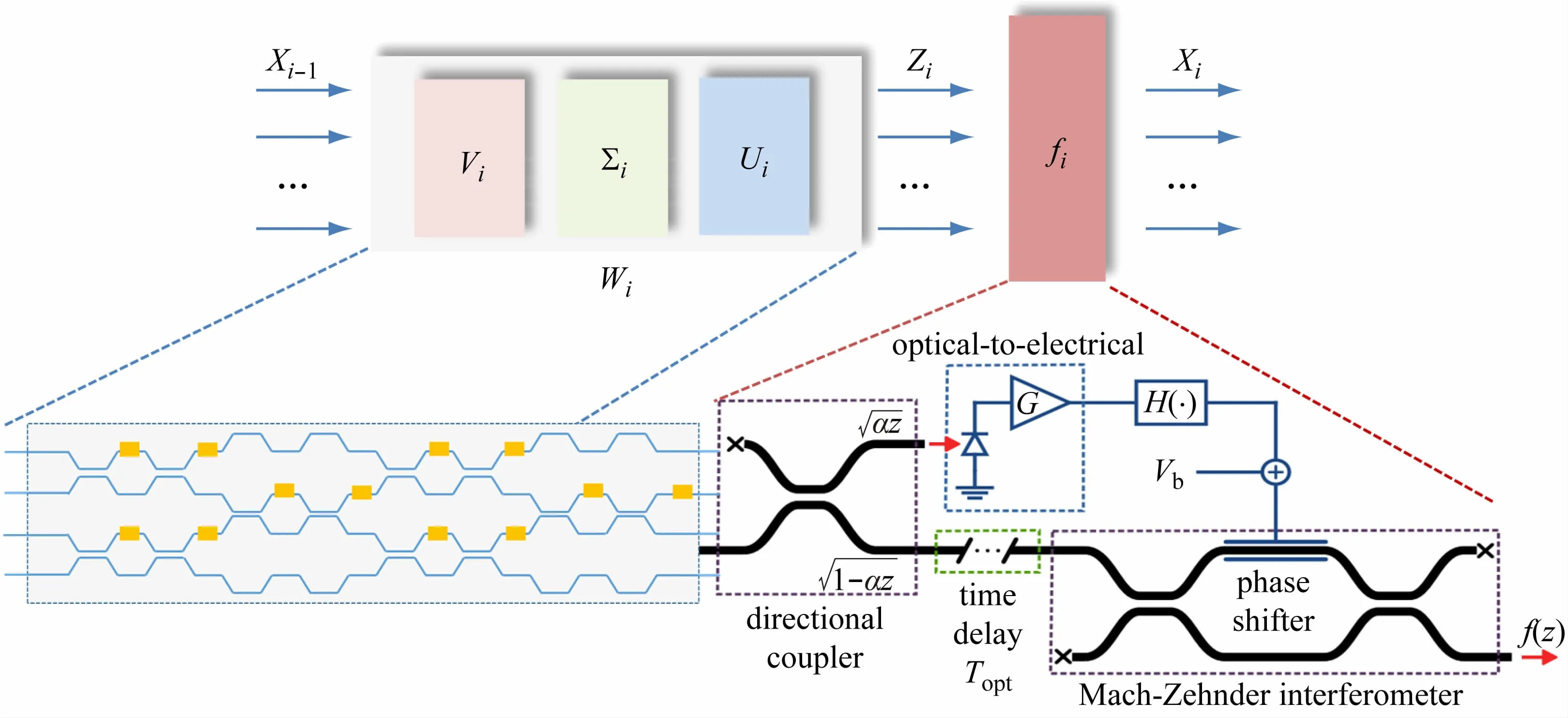
图3 单层前馈神经网络实现示意图

1.3 光学非线性单元

ONU采用一种用于ONN 的非线性激活函数架构，该架构通过将一小部分光学输入功率转换为电压来实现光学到光学的非线性响应。图3 右下部分为光到光激活函数实现的示意图，该函数通过将一小部分光输入信号z转换为电信号，然后在原始光信号通过干涉仪时对其剩余部分进行强度调制，实现非线性响应。这种非线性电光激活函数架构可以重新编程以合成各种不同的非线性响应。激活函数

式中：Vπ为在相位调制器中引起π 相移所需的电压；Vb为激活移相器的电偏置。

相位增益参数定义为：

式中：α为部分输入光功率；G为增益；R 是光电探测器的响应度。式（5）表明每单位输入信号的相移量可以通过增益和光电二极管响应度增加，或者通过将较大比例的光功率转换为电域增加。Vb是确定非线性响应的重要因素，不同电偏置可以合成不同的激活函数响应。

2 伴随变量法片上训练方法

伴随变量法（Adjoint Variable Method，AVM）是通过器件的强度测量来获得后向传播中光路的参数，这与常见的神经网络计算梯度的方法类似。通过对每一个参数梯度的计算，判断出该参数优化的方向，较快地找到最优的训练模型［12］。具体步骤如下：

步骤1用光载波正向输入信号XL－1到OIU集成芯片，记录光信号在经各个相位偏移器时电场强度的幅度，该电场强度即为源场。

步骤2反向输入信号

式中：⊙为逐元素向量相乘；ΓL＝（XL－T）H为步骤1中实际输出与理想输出信号的差值；f′L（ZL）为最后一层非线性激活函数的导数值。记录各个相位偏移器中电场强度的幅度大小。该电场强度即为伴随场。

步骤3将步骤2 中伴随场的等效正向输入信号XTR，与步骤1 的原始输入信号XL－1叠加输入OIU，发生干涉，记录各相位偏移器强度。

步骤4用求和公式计算源场和伴随场的矢量积，取矢量积的实部即为代价函数关于移相器相位的梯度值：

式中，k0为自由空间波数。

步骤5利用梯度下降法对每一个相位偏移器的相位值进行更新，如图4 所示。

图4 伴随变量法片上训练过程

最后重复步骤1～5 不断更新迭代移相器中的相位值来减小代价函数，最终实现片上训练的完整过程。

3 光神经网络实验方案设计

3.1 neuroptica包介绍

neuroptica包是纳米级神经网络的柔性芯片级仿真平台，包括components、componet ＿ layers、layers、Losses、models、nonlinearities、optimizers、utils等，为模拟光学神经网络提供了广泛的抽象层次，可模拟芯片操纵单个移相器的排列和特性，也能通过堆叠网络层来设计ONN。本文使用neuroptica实现ONN建模。

3.2 MNIST手写体数字识别实验设计

3.2.1 数据预处理

手写数字图取自MNIST数据库，图片大小为28 ×28 像素。为减少执行训练过程所需的计算资源，预处理步骤将图像进行傅里叶变换：

式中：g（m，n）为图像中位置（m，n）处的像素的灰度值，其中傅里叶空间轮廓主要集中在小的kx和ky周围。本文将数据限制为具有最小的的N个系数。

傅里叶变换在光学领域可通过标准组件，如透镜和空间滤波器直接实现，N个复值系数c（kx，ky）可由N维ONN处理，而使用实值神经网络处理相同的输入需要两倍大的维度。在ONN广泛应用。

3.2.2 实验步骤

计算图像二维傅里叶变换实现对手写数字集的预处理，转换为复值向量用作ONN的输入。标签的处理则采用了one-hot的思想，将原来的回归问题变为一个分类问题。实验流程如图5 所示。

步骤1 将MNIST 手写体中60 000 张图像作为训练集，分512 个批次通过网络输入，剩余的10 000张图像作为测试集。

步骤2 将图像数据转换为傅里叶空间表示。

步骤3 获取kx＝ky＝0 的N个傅里叶系数，以实现图像降维操作作为输入数据。

步骤4 利用neuroptica 包中函数构建L层的ONN

步骤5 构建drop-mask将最终输出减少到10 个分量。记录10 个输出的强度并通过它们的总和进行归一化，创建一个概率分布，可与从0～9 的数字的one-hot编码进行比较。

步骤6 不同参数下实现ONN 模型构建，并分析对比手写体数字的识别结果。

3.2.3 训练与识别实现

在Python的Tensorflow框架下，使用neuroptica软件包，搭建ONN 网络，设定参数配置，实现模型训练，部分代码如下所示：

4 实验结果及分析

4.1 不同参数仿真结果对比分析

通过设计不同参数下的仿真，实现结果对比，包括输入不同图像维度N、有无激活函数和激活函数配置参数等。

4.1.1 不同输入维度下的实验对比分析

设网络电光激活函数参数配置为gφ＝0.05π、φb＝1.00π和α ＝0.1，当N为16、36 和64 时，分别得到一个4 ×4、6 ×6 和8 ×8 的矩形作为输入数据，传入3层ONN进行训练。图6 中蓝色的实线表示N ＝16，红色表示N ＝36，绿色表示N ＝64，图6（a）反映了输入维度和模型预测准确率成正比，图6（b）显示训练期间的交叉熵损失收敛速度随着输入的维数增加而增加。

4.1.2 有无激活函数对比

输入具有N＝16 个傅里叶分量的3 层ONN，其电光激活函数配置保持不变。比较加入激活函数的ONN和无激活函数的ONN的分类精度。图7（a）显示非线性激活函数在训练期间和训练后显著提高了ONN的性能，带有电光激活函数的ANN 最终预测结果准确率达到了90%以上，而未带有电光激活函数的ANN最终预测结果的准确率仅有83%。由图7（b）可见，加入非线性激活函数后，交叉熵损失值远远小于未加入激活函数的模型。

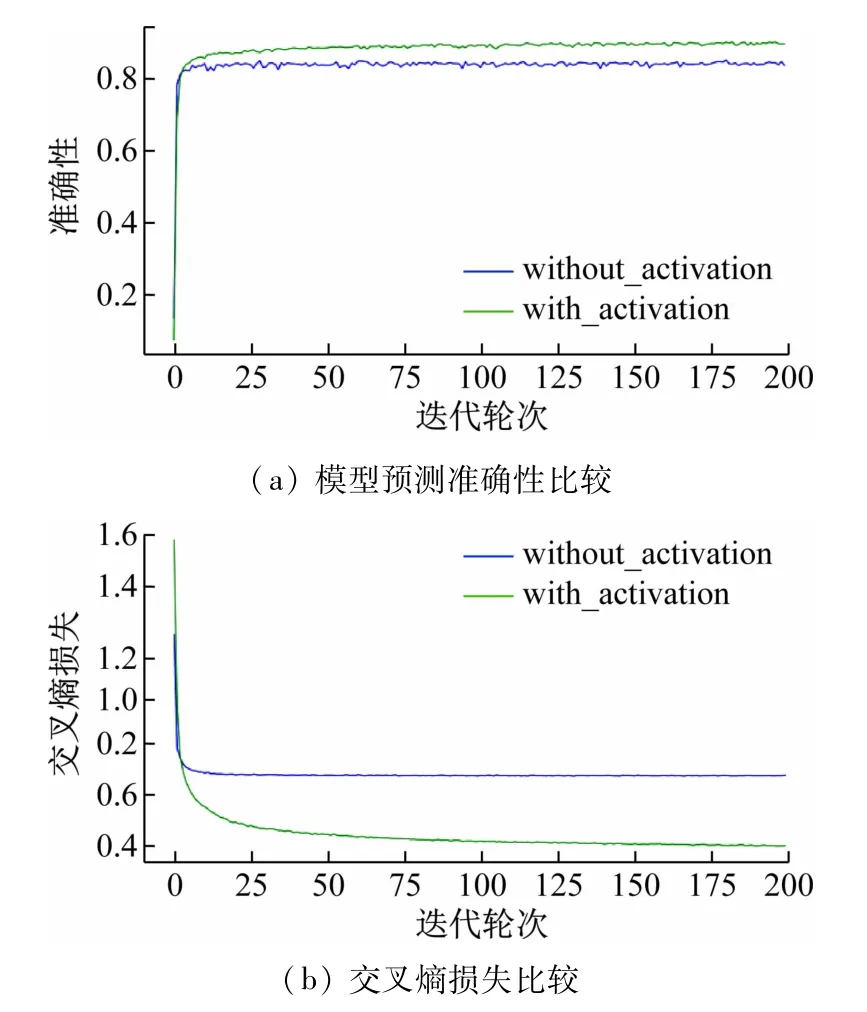
图7 有无激活函数对比实验图

4.1.3 激活函数调参对比实验

激活函数参数包括前馈相位增益gφ，PD 电量α和相位偏移φb。以分析不同相位偏移φb为例，图8 不同颜色实线代表不同的φb值在最后训练得到的平均预测准确率，从放大图中看出，当φb＝－1.5π 时，预测准确率最大，可以达到92.5%。

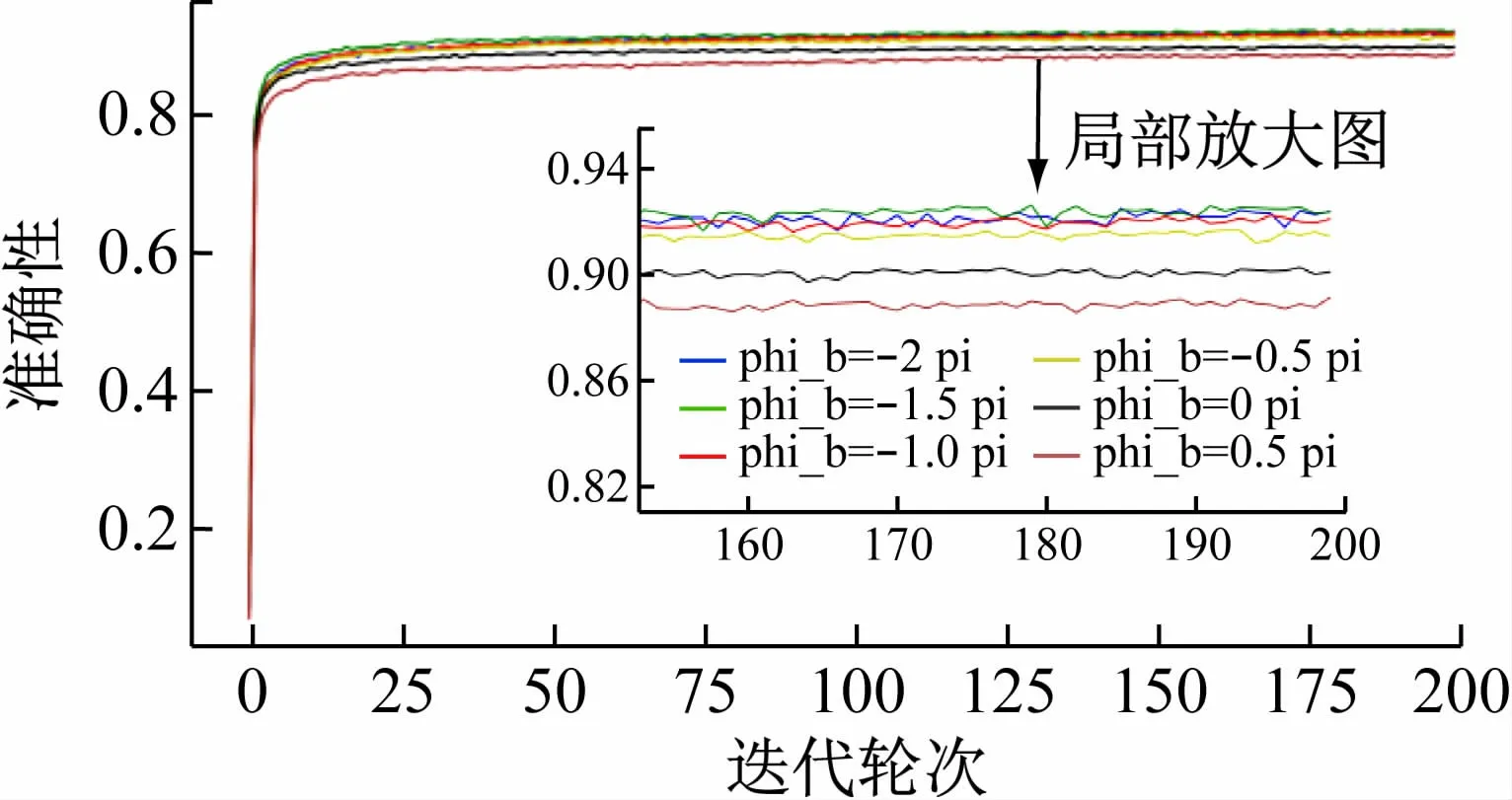
图8 参数φb对于预测准确率影响

4.2 手写字体识别

根据上述激活函数调参对比仿真，激活函数最优参数配置为gφ＝0.3π、φb＝－1.5π和α ＝－0.3 及输入维度N＝16，同时网络以epoch ＝200，batch＿size ＝256 的参数进行训练，输入10 ×104组测试集，最终得到的预测值接近93%，绘制的混淆矩阵如图9 所示。

图9 手写数字识别混淆矩阵

4.3 扩展实验

学生还可自主搭建ONN 拓展应用于其他问题解决上，例如二元分类器、异或逻辑功能以及鸢尾花分类等，图10 为应用结果示例。

图10 应用拓展

5 结语

本文基于python环境下，利用neuroptia 设计和仿真实现基于ONN的手写字体识别实验，通过仿真运行帮助学生梳理合成光学到光学非线性的架构和ONN的相关知识，证实了光电激活函数搭配的ONN在机器学习问题上的应用，从实践中掌握多学科交叉研究的能力，学生还可自主搭建ONN应用于其他机器学习问题上，以提高学生的创新能力和实践动手能力。