Weak localization in disordered spin-1 chiral fermions

Shaopeng Miao(苗少鹏), Daifeng Tu(涂岱峰),†, and Jianhui Zhou(周建辉)

1Anhui Key Laboratory of Condensed Matter Physics at Extreme Conditions,High Magnetic Field Laboratory,HFIPS,Chinese Academy of Sciences,Hefei 230031,China

2University of Science and Technology of China,Hefei 230026,China

Keywords: magnetotransport,weak localization,chiral fermions

1. Introduction

Disorders usually break crystal translational symmetry and play a crucial role in the transport properties of electrons in solids.[1]It has been shown that strong disorders could induce metal-to-insulator transition, leading to Anderson insulators.[2]In the quantum diffusion regime where the mean free path is much shorter than the phase coherent length and the size of the system, electrons remain the phase coherence during the impurity scattering.[3]Consequently, this weak disorders could give rise to noticeable contribution to the classical Drude conductivity at low temperature (Fig. 1(b)),manifesting as weak localization (WL) or weak antilocalization (WAL).[4]WL and WAL correspond to the constructive and destructive interference between time-reversed scattering paths, respectively (Fig. 1(a)). The quantum interference corrections(WL/WAL)strongly depends on the specific properties of the electronic system including the dimensionality, the types of disorders, the form of the spin–orbit coupling, the Berry phase of electrons.[5–9]Recently, the WL effect has been used to identify the nature of two-dimensional(2D) massless Dirac electrons with nontrivial Berry phase in the context of graphene[10,11]and surface states of topological insulators.[3,12–15]

Three-dimensional (3D) topological semimetals, a new state of quantum matter, support massless fermions such as well-known Dirac and Weyl fermions at discrete points in the Brillouin zone.[16–18]The nontrivial topology and unique energy dispersion of massless fermions could lead to a great variety of novel quantum phenomena, such as chiral anomaly and the resulting negative magnetoresistance,[19–25]and chiral sesudomagnetic effect.[26–28]Very recently, first principles calculations suggest that the chiral crystalline family of transition metal silicides, including CoSi, RhSi, RhGe, and CoGe,[29]has been recently proposed as ideal candidates to host unconventional chiral fermions characterized by a large monopole charge,some of which have been observed experimentally through angle-resolved photoemission spectroscopy(ARPES), transport and infrared optical spectroscopy.[30–32]In this work,we focus on the three-component chiral fermion or spin-1 chiral fermion[33]that is characterized by the combination of two Dirac-like bands and a flat band with threefold band crossings(Fig.1(c)),carrying a larger monopole charges of±2. These spin-1 chiral fermions exhibit fantastic physical properties, such as helical surface states,[30–32,34]unusual magnetotransport,[35,36]the circular photogalvanic effect,[37]and unconventional superconductivity.[38]The investigation of the impact of disorders on the quantum transport of new chiral fermions would be highly desired.

In this work, we give a theory of magnetoconductivity for spin-1 chiral fermions due to quantum interference in the presence of scalar impurities by using Feynman diagram techniques. We find a WL correction to the Drude conductivity,which is consistent with the Berry phase analysis. In addition, the impact of anisotropic disorders is also discussed in the weak anisotropy limit.

The paper is organized as follows. In Section 2, we introduce the effective model the spin-1 chiral fermions and calculate the monopole charges. In Section 3, we calculate the Drude conductivity and quantum interference corrections from both the intravalley and intervalley scattering from isotropic disorders. In Section 4, we consider the anisotropic disorders and calculate the quantum interference conductivity in the weak anisotropy limit.

Fig.1. (a) Backscattering of electrons along two time-reversed paths in disordered metals. The blue and red lines in (b) are the magnetoconductivity signature of WL and WAL, respectively. (c) The energy dispersion of the spin-1 fermions.

2. The effective model

According to the Fermion doubling theorem,[39]fermions with opposite chirality usually appear in pairs in solids. Thus we consider a pair of valleys for spin-1 fermions located at±kc

where the Fermi velocity is aboutvF～6.7×107cm/s,[40]¯his the reduced Planck constant,ψkχ=（ψkχ,1,ψkχ,0,ψkχ,-1）is a three-component field operator,χ=±is the valley index,andkis measured from each valley.L=(Lx,Ly,Lz) represents three 3×3 matrices with the pseudospin equaling to 1,and in the bases of eigenstates ofLz,the Hamiltonian near each valley can be written as

The corresponding eigenenergies areEχλk=λvF¯hk,withλ=±1,0 being the band index. Without loss of generality,we assume that the Fermi energyEF＞0 lies in the conduction band and is far away from the band touching point,so as to ignore the interband scattering.The wave functions of the conduction bands in the two valleysχ=±are given as

where the angles are defined as cosθ=kz/|k| and tanφ=ky/kx.|-,k〉can be gotten by replacingkwith-kin|+,k〉,namely,θ →π-θ,φ →π+φ. Note that we here choose this gauge to keep the eigenstates being single-valued in the limitθ →0. The Berry curvature of each valley is defined asΩχ(k)=∇k×〈χk|i∇k|χk〉=[41]Then the relevant monopole charge of the spin-1 fermions can be calculated as

Note that the phase difference between the two time reversal scattering paths is equivalent to the Berry phase along the loop formed by the two paths.[7]For the spin-1 fermions whose Berry phase is 2π, the time reversed scattering paths will interfere constructively, leading to a negative correction to the classical Drude conductivity,that is,the WL effect.

3. Magnetoconductivity for isotropic disorders

In this section,we investigate the impacts of the disorder that is described by the Dirac delta function

whereRidenotes the position of the impurity, anduiis the corresponding scattering intensity,ui=u0for the intravalley scattering,ui=uIfor the intervalley scattering. We utilize Feynman diagram techniques to evaluate the semiclassical Drude conductivityσscas well as the relevant the quantum interference correction to the conductivityσqi,which contains the parts from the intravalley scatteringand the intervalley scattering.

3.1. Semiclassical Drude conductivity

In order to calculate the conductivity,we need the disorder modified velocity through the vertex correction,as shown in Fig. 2(a). Then the semiclassical Drude conductivity(Fig.2(b))can be written as

whereVis volume of the system,vχikis the velocity of electrons in the conduction band near the valleyχ,vχik==vFk/k. The corrected velocity ˜vχikby the disorder scattering can be evaluated from the ladder diagram(Fig.2(a)). The retard and advanced (R/A) Green functions are(ω)=1/(ω-ξk±i),withξk=Ek-EFandEk=vFh¯k.Hereτis the total disorder scattering time[42]and is the inverse of selfenergy from the impurity scattering including the intravalley and intervalley scattering. Within the first-order Born approximation,τcan be written as[6]

Here, the disorder correlation function with impurity average is defined as

with

Due to the isotropic energy dispersion and the disorder potential,we could assume=and put it into Eq.(11). After cumbersome calculations,we find

It has the same form as that of the conventional twocomponent Weyl fermions,[6]except a difference of prefactor of 2. The Drude conductivity is usually expressed asσsc=e2NFDin terms of the diffusion coeffciientD=τηv.

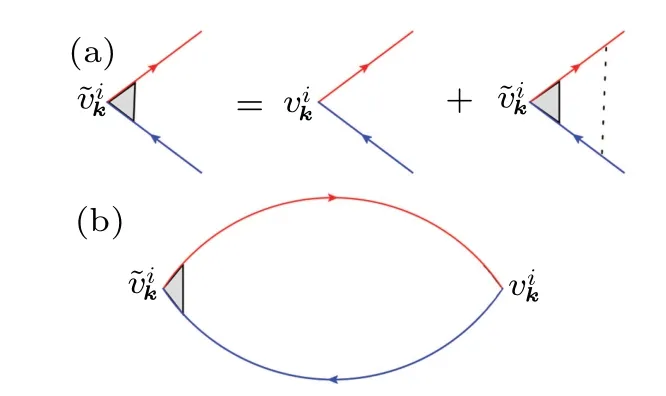
Fig.2. (a) The Feynman diagram for vertex correction and (b) the diagram for the semiclassical Drude conductivity σsc. The red and blue arrowed solid lines denote electron’s retard/advanced Green functions,respectively. The dashed line denotes impurities scattering.

3.2. Conductivity correction from quantum interference σqi

The quantum interference correction to the Drude conductivityσqiusually contains two parts: the intravalley cooperonsand the intervalley cooperons. The total quantum interference conductivity correctionσqiis the sum of the two parts:

We first consider the conductivity correction from the intravalley scattering as shown in Fig.3,

where factor 2 comes from two topological equivalent diagrams, and the conductivity corrections from the bare and dressed Hikami boxes are expressed as[43]

The quantum interference effect comes into the conductivity correction by the maximally crossed diagrams which are called cooperons. For the intravalley scattering, the dressed cooperonΓk1,k2can be obtained through the Bethe–Salpeter equation(BSE),as shown in Fig.3,

Fig.3. The Feynman diagrams for quantum interference correction to conductivity from the intravalley scattering. (a) The bare Hikami box for the intravalley scattering. (b) The dressed Hikami box for the intravalley scattering. (c)The BSE for the intravalley cooperons.

The conductivity correction in Eqs.(16)and(17)can be finally written as

whereQ0andχ0are the cooperon gap and the corresponding weighting factor, respectively, and their values are given in Appendix A. The total quantum interference conductivity correction from the intravalley scattering becomes

It clearly gives rise to a WL effect,which is consistent with the Berry phase argument. We note that the intravalley scattering corrected conductivityonly keeps the term that depends on the relative intensity of the intervalley scatteringηI,and in the limitηI→0 the ratio of bare Hikami boxes to dressed Hikami boxes is

It means that the correction for the bare and dressed Hikami boxes from the intravalley scattering will cancel each other out. In Table 1, we compare our results with those of 3D single Weyl fermions[6,44]and double Weyl fermions.[7]Note that this cancelation may be removed by anisotropic energy dispersion, anisotropic disorders and higher order impurities scattering in the dressed Hikami boxes. We will examine the anisotropic disorders in the next section.

Table 1. Comparison among 3D single-Weyl fermions, 3D double-Weyl fermions,and 3D spin-1 fermions,with±N being the monopolecharge.

We would like to consider the conductivity contributions from the intervalley cooperons:

as shown in Fig.4,which consists of one bare Hikami box

and two dressed Hikami boxes

Note that each of the two dressed Hikami boxes contains two topological inequivalent diagrams.

Fig.4. The Feynman diagrams for quantum interference corrected conductivity from the intervalley scattering: (a) the bare Hikami box for the intravalley scattering,(b)and(c)the dressed Hikami boxes for the intravalley scattering,and(d)the coupled BSEs for the intervalley cooperons.

The intervalley cooperons, as shown in Fig.4(d), satisfy the coupled BSEs:[6]

are the bare cooperons and the detailed derivations are given in Appendix B. Then, the conductivity corrections in Eqs. (24),(25)and(26)from the intervalley scattering cooperons can be written as

whereQiandχi(i=1,2,3) are the cooperon gaps and the corresponding weighting factors, respectively, and their values are given in Appendix B. The total quantum interference correction to the conductivity is the sum over all the above Feynman diagrams:

The phase coherence length is the function of temperatureTand has the formlφ∝T-p/2,[45]wherepis related to the decoherence mechanism,p=3/2 for the electron–electron interaction,p=3 for the electron–phonon interaction.[1]As shown in Fig. 5(a), at low temperatures, we havelφ ≫lB ≫l, and the magnetoconductivity (32)δσ(B)∝, wherel=is the mean free length. As the temperature increases,lφbecomes shorter,and forlB ≪l,lB ≪lφ,the magnetoconductivity(32)becomesδσ(B)∝B2. At the sufficiently high temperatures,the phase coherence length and the mean free length are comparable,the WL correction to magnetoconductivity disappears.

As aforementioned, the dressed and bare Hikami boxes from the intravalley scattering cancel each other out for the isotropic Delta disorders,only the contribution from the intervalley scatteringηIremains. WhenηI+ηa=5/3, the intervalley cooperons gaps are 0,the intervalley cooperons have a major contribution to the magnetoconductivity. The WL effect becomes pronounced,and increases withηI,as shown in Fig.5(b). However,whenηI+ηa/=5/3,the magnetoconductivity of the intravalley cooperons and that of the intervalley cooperons are both small, so the magnetoconductivity curve almost coincides with the horizontal axis for any finites values ofηIandηa.

Fig.5.The magnetoconductivity δσqi(B)for different phase coherence length lφ at ηI+ηa=5/3 and l=10 nm in(a),and for different ηI and ηa at l=10 nm and lφ =1000 nm in(b).

4. Impacts of anisotropic disorder

In this section, we would like to investigate the impacts of the anisotropy of impurities on the quantum transport properties of spin-1 fermions. Specifically, we consider the anisotropic impurity potentialU′=∑i uδ(r-Ri),whereu= diag{u0,u0,(1+η)u0}. The scattering time becomes angle-dependent and has the form

It can be seen that in the weak anisotropy limitη →0, the scattering time reduces to the isotropic oneτ0. As a result,the renormalized velocity becomes anisotropic:

and the renormalized velocities can be obtained by solving the following iterative equation for the vertex correction:

After some complex calculations,we find that the coefficients of renormalized velocity in thexandydirections as follows:

and in thezdirection

Note that in the limitη →0, the renormalized velocity recovers that in the presence of the isotropic disorder=2,η(2)i=0. We first calculate the Drude conductivity to the first order ofηin three directions:

It is clear that anisotropic disorders could cause anisotropic transport even for electrons with an isotropic energy dispersion.

The quantum interference correction to the conductivity from the bare and dressed Hikami boxes can be directly calculated as

and the cooperons for the anisotropic disorder are given in Appendix C.The total quantum interference corrected conductivity in thexorydirection is

In thezdirection,the bared Hikami box gives

and the dressed Hikami box gives

Following the similar calculations,we can obtain the total conductivity in thezdirection as follows:

the magnetoconductivities in thex,yandzdirections can be summarized as

It can be seen that anisotropic disorders could lead to anisotropy of quantum interference correction of conductivity in different directions. Note that in the absence of anisotropy of disorders,η →0, we could reproduce the result for the isotropic disorder.

5. Conclusions

In summary, we have investigated the quantum interference magnetoconductivity of spin-1 chiral fermions in the presence of isotropic and anisotropic disorders by using the method of the standard Feynman diagram. We find a WL correction to the classical Drude conductivity,consistent with the 2πberry phase. The anisotropy of disorders could remove the cancelation of the coherent backscattering from bared Hikami cooperon and non-backscattering from the dressed Hikami ones in the intravalley scattering. The predicted novel transport properties due to quantum interference of new spin-1 chiral fermions can be verified experimentally.

Acknowledgements

The authors thank Yixiong Ren for useful discussion.The work was partially supported by the High Magnetic Field Laboratory of Anhui Province,China.

Appendix A

In this appendix, we show the process of solving the Bathe–Salphter equation for the intravalley scattering. To solve this iterative equation, we use the bare cooperon as the initial value

and the corresponding full cooperon can be obtained through the BSE,as shown in Fig.3,

Replacing the summation by integration, the BSE in Eq.(A2)can be written as

The radial integral can be calculated as[6]

To get the form of the dressed cooperonΓk1,k2, we can first substitute the bare cooperon(A1)as the zeroth order trial solution into the right side of BSE in Eq. (A2), and obtain the first-order solution as follows:

After some calculations, we can find thathas no more linearly independent terms than, which indicates that this set of polynomials becomes closed during iteration.Therefore,the full cooperonΓk1,k2can have the form

To further determine these undetermined coefficients,we put Eq.(A7)into the BSE in Eq.(A2),and obtain a set of linear equations. In the limitωm →0,these coefficients have the form

It can be seen that,in the limitq →0,only the first term becomes divergent and has the form

Appendix B

In this appendix, we give the detailed calculation of the dressed cooperon for the intervalley scattering. Similarly,the intervalley cooperons, as shown in Fig. 4(d), satisfy the coupled BSEs[6]

and substituting them into the coupled BSEs in Eqs.(B1)and(B2),we finally get the coefficients of the full cooperons

where the weighting factors are

and the cooperon gaps are

Appendix C

In this appendix,we turn to evaluate the quantum interference correction to the Drude conductivity. The bare cooperon for the anisotropic disorder becomes

We then assume the dressed cooperon as

where the undetermined coefficients can be obtained by solving the BSE in the similar mean above. In the limitq →0,we find that only the termA1diverges and has the approximate dressed cooperon as

with

In the limitη →0,we have→0,and the dressed cooperon is divergent for smallq →0.