Correlated states in alternating twisted bilayer–monolayer–monolayer graphene heterostructure

Ruirui Niu(牛锐锐), Xiangyan Han(韩香岩), Zhuangzhuang Qu(曲壮壮), Zhiyu Wang(王知雨),Zhuoxian Li(李卓贤), Qianling Liu(刘倩伶), Chunrui Han(韩春蕊), and Jianming Lu(路建明),‡

1State Key Laboratory for Mesoscopic Physics,School of Physics,Peking University,Beijing 100871,China

2Institute of Microelectronics,Chinese Academy of Sciences,Beijing 100029,China

3University of Chinese Academy of Sciences,Beijing 100049,China

Keywords: twisted graphene heterostructure,Pomeranchuk effect,correlated states,van Hove singularity

1. Introduction

Twisted van der Waals heterostructures provide unprecedented capability to design andin-situcontrol electronic correlation,leading to the discoveries of abundant physical properties in a pure carbon system,[1–24]such as correlated insulators, superconductivity, magnetism, quantum anomalous Hall effect and strange metal. Correlated electrons arise from the flat band that is generated by moir´e superlattices at the twisted interface, so that the twist angle –e.g., in twisted bilayer graphene (TBG) –is critical to observe correlated phenomena. Away from the magic angle of 1.05°, superconductivity as one of the essential properties in TBG is suppressed at merely 1.25°,[25–29]challenging the robustness of practical device applications. To overcome the narrow angle range, another ingredient of the flat band, i.e., the dispersion relation of the constituent material itself, is proved to be extremely useful in many systems. For instances,Bernal bilayer graphene is endowed with a‘Mexican hat’[30,31]dispersion at the edge of conduction and valence bands under out-of-plane displacement fields, hence the twist angle could be extended to 1.5°without losing the electronic correlation.[5–7,32]Transition metal dichalcogenides naturally have heavy electron/hole masses, whose large-curvature band edges allow the correlation to survive at twist angles over 5°.[33]Another intriguing attempt is to stack bilayer graphene with monolayer graphene,despite that the two have distinct dispersions. It turns out that the structural asymmetry gives rise to many interesting properties like tunable van Hove singularity (VHS),[34]asymmetric symmetry breaking phases,[35]and (quantum) anomalous Hall.[13,35]These fruitful results encourage wider exploration in more versatile systems.

A Bernal bilayer and twisted bilayer graphene both have weakly dispersive band edges. By exploiting these characteristics,we stack a Bernal bilayer graphene and two monolayer graphene(hence twisted bilayer)in an alternating way,dubbed as AT211G,to investigate correlated properties. Surprisingly,even at a very large angle～1.74°,resistive peaks originating from electronic correlation can be found in both conduction and valence bands. The peaks also depend sensitively on the direction of the displacement fields, which can be attributed to the asymmetric crystal structure and hence band structure.With further characterization of varying temperature in both out-of-plane and in-plane magnetic fields,we identify that the correlated states at filling factorsv=1,-3 may originate from the Pomeranchuk effect.The findings are believed to stimulate extensive exploration of various multilayer hybrid systems.

2. Basic characterization and methods

Figure 1(a)shows the schematic device, where the alternating twisted bilayer–monolayer–monolayer graphene is encapsulated by hexagonal boron nitride(hBN).The bottom gate is made of thick graphite flake to electrostatically screen the charged defects buried in silicon substrates, whereas the top gate is a metallic film. The three constituent graphene flakes come from a single flake exfoliated from a natural graphite crystal. Following the well-established dry transfer method,the pre-cut flakes were stacked sequentially with a twist angle ofθ=1.7°, consistent with the electrically measured 1.74°(see below). Optical characterization of the multilayer heterostructure is displaced in Fig. 1(b), in which the graphene layers are enclosed by dashed lines with colors corresponding to that in Fig. 1(a). We further checked the homogeneity of twist angles over the entire sample, by measuring transfer curves from different parts. As compared in Fig.1(c), all the resistive features coincide with each other, suggesting a low angle disorder. In the following, we present only the result between pins 7–11 (inset of Fig. 1(c)). Displacement fieldDand filling factorvare defined asD/ε0=(εbVb/db–εtVt/dt)/2 andv=4n/n0, wheren=ε0(εbVb/db+εtVt/dt)/e,n0is for the full filling of a flat band,εb(t)is the relative dielectric constant of the bottom(top)gate,anddb(t)is the thickness of the bottom(top)gate.

3. Results and analysis

3.1. Asymmetric performance

Figure 1(d)plots the phase diagram as a function ofDandv.The most significant feature is the asymmetric performance,not only between electron and hole,but also between positive and negativeD. Let us look at the charge neutral point(CNP)firstly. At-0.5 V·nm-1＜D/ε0＜0.25 V·nm-1, the energy gap is not opened, manifesting as a small resistance, which could also be seen atv=0 in Fig. 1(c). AsDincreases, the CNP peaks do not grow symmetrically along positive and negative directions. Similar asymmetry could be found for other bandgaps(v=±4)and correlated resistive peaks at fractional fillings. Atv=-2,in the region ofD ＞0 it starts to develop atD/ε0as low as 0.1 V·nm-1(even without the presence of a CNP gap),peaks atD/ε0=0.4 V·nm-1,and then gradually decays. In contrast, forD ＜0, there is nothing but metallic states. An opposite case takes place on the electron side,where it is theD ＜0 regime that exhibits correlated peaks atv=1,2 and 3.

Such an asymmetry could find its origin in an intuitive picture. ForD ＞0(D ＜0),electron(hole)wavefunctions are pushed away from the twisted bilayer, so that it is the Bernal bilayer graphene that contributes to the correlated features.On the one hand, this is reasonable, as the twist angle of our device is 1.74°which is too large for a TBG to exhibit correlation. On the other hand,such correlated peaks at hole sides have not been found in twisted mono-bilayer graphene[13,34,35]or twisted double bilayer graphene.[5,7,32]A detailed theoretical calculation is needed to give some hints from the band structure.

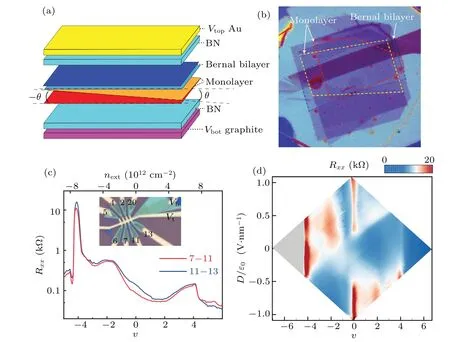
Fig.1. Electric characterization of alternating twisted bilayer–monolayer–monolayer graphene with θ =1.74°. (a)Schematic of the device.(b)Optical characterization of the multilayer heterostructure,where the graphene layers are enclosed by dashed lines. The colors correspond to that in panel(a). (c)The angle homogeneity across the entire sample can be seen by consistent resistive features. Inset: Optical image of the finished device with pin indexes. (d)Phase diagram as a function of displacement field and filling factor.

3.2. Tunable van Hove singularity

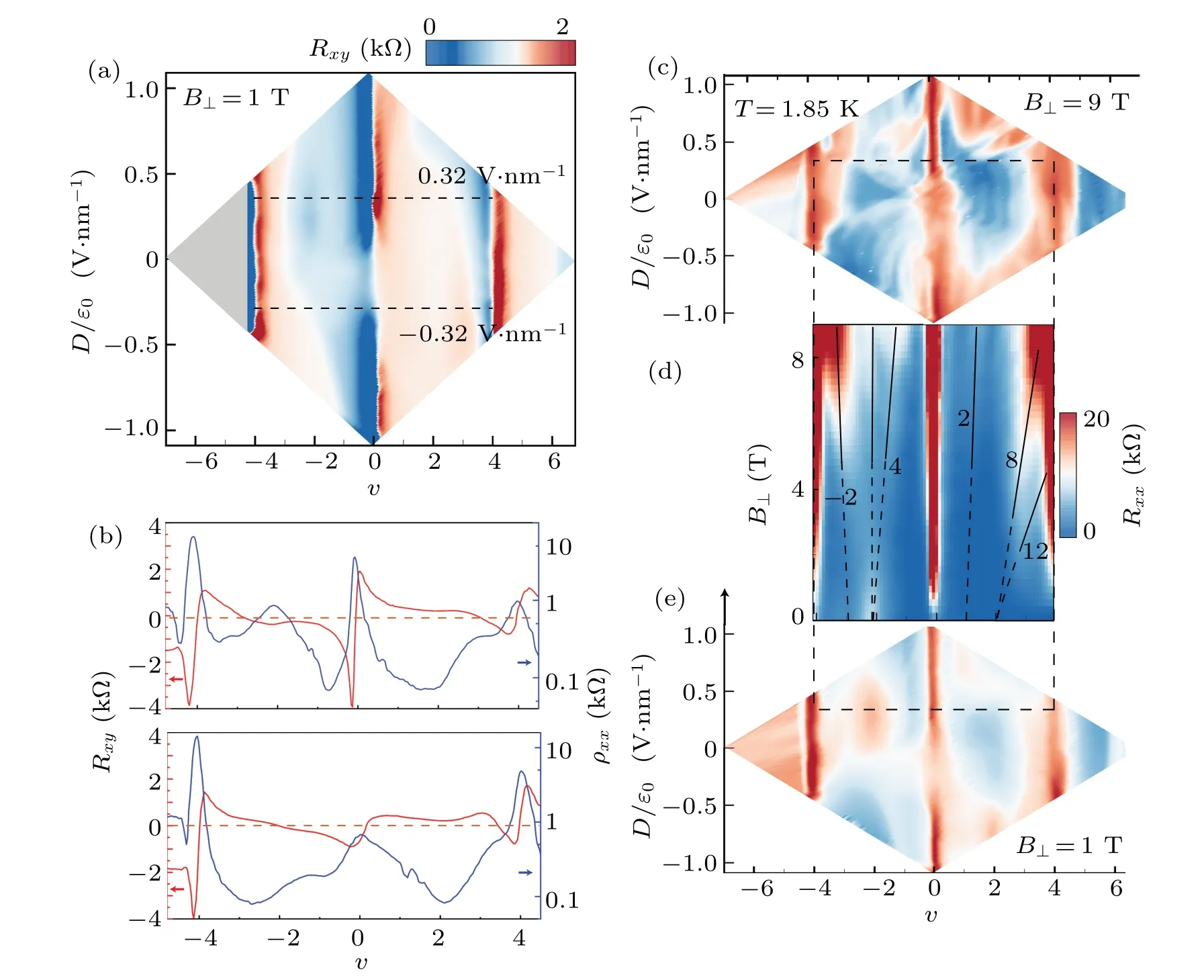
Fig.2. Tunable van Hove singularity and additional correlated states in perpendicular magnetic fields. (a)The van Hove singularity denoted by zero Hall resistance(white color)is highly tunable by displacement fields. (b)Asymmetric response of Hall carrier density can be identified at positive and negative D. (c)–(e) Phase diagrams measured at 9 T (c) and 1 T (e) are connected by Landau fan characterization (d) at D/ε0=0.32 V·nm-1. In(b),various Landau levels emanate from fractional filling of the flat band,such as(-2,-3),(4,-2),(1,2),(2,8)and(2,12). Here the first number is LL index and the second is filling factor.

Experimentally,prominent features of the band structure can be unveiled by Hall effects characterization. Figure 2(a)plots a phase diagram, where blue and red regions represent hole and electron characteristics and the white color is for vanishing Hall signal. Besidesv=0,±4 where electron–hole puddles will balance to result in zero Hall resistance, white curves with irregular shapes can also be observed inside the flat band, which is due to van Hove singularity. Again, it is asymmetric with respect to electron/hole or±D. To see the asymmetry more clearly, the Hall resistances are plotted forD/ε0=0.32 V·nm-1(upper) and-0.32 V·nm-1(lower) in Fig.2(b). The four VHS points arev=-2.94 andv=+2.96(D ＞0),v=-1.92 andv=+3.44(D ＜0),respectively. The traces of VHS as a function ofDplace a strong constraint for the band structure calculation in the future.

3.3. Additional correlated states

Careful examination of Fig.2(a)reveals another correlation feature – a kink ofRxyaroundv=-2 (D ＞0), which is the remanence of flavor symmetry breaking. In twisted mono-bilayer graphene and other systems(of proper twist angles) that exhibit much stronger correlation,[5–7,13,18,32,34,35]the Hall signal evolves from the present kink to ‘reset’. This correlation feature can be better visualized inRxxsignal, as shown in Figs. 2(c)–2(e). In a magnetic fieldB⊥= 9 T(Fig. 2(c)), complicated features are observed, which can be resolved in the Landau fan characterization (Fig. 2(d)). Using a pair of quantum numbers (t,s) satisfying the Diophantine equationν=tφ/φ0+s,whereφis the magnetic flux per moir´e unit cell,andφ0is the magnetic flux quantum,we identify Landau levels(LLs)emanating fromv=-3,+1 and+2,in addition tov=-2. Interestingly, correlated state (CS) atv=+1 already appears inB=1 T (Fig. 2(e)). Another unexpected feature is the LL(4,-2),indicating electrons rather than holes residing on the Fermi surface, in contrary to the positiveRxyshown in Fig. 2(a). These effects suggest that magnetic fields not only generate LLs but also play a nontrivial role in the reconstruction of band structures (probably associated with flavor symmetry breaking).

3.4. Pomeranchuk effect at v=1

Besides the correlated states,a widely observed phenomena among various twisted systems is isospin Pomeranchuk effect. This entropy driven localization was originally discovered in3He,[36]in which heating unexpectedly turns a liquid into a solid.The underlying mechanism is the fluctuating magnetic moment of nuclear spin of3He that provides substantial entropy at high temperature. In TBG,the charge carriers and their isospin correspond to nuclear (i.e., atoms) and nuclear spin, respectively, hence the crystallization of atoms in turn means the localization of charge carriers. As a result,one can see a higher resistance peak (stronger localization) at higher temperatures. Furthermore,it was found in TBG the electron spin rather than the valley degree of freedom bears the fluctuating moment.[37,38]

Here in our AT211G, atD/ε0=-0.6 V·nm-1we find a similar temperature dependence atv=1. Figure 3(a)shows the non-monotonic evolution of the correlated peaks.The peak position is not pinned tov=1 but rather shifts with temperature (red dashed line). To quantify carrier localization, the effective peak magnitudeR*is obtained by subtraction of a smooth background (see illustration of 10 K in the inset of Fig.3(a))and plotted in Fig.3(b)forv=1,2. In-plane magnetic fields are also applied to quench the fluctuation of spin moment and hence entropy. However,the negligible effect observed in Fig. 3(c) and also Fig. 3(b) indicates a weak coupling between magnetic fields and spin, in respect of which AT211G is similar to twisted trilayer graphene[39]but contrary to TBG.[37,38]

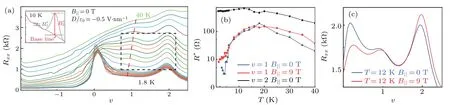
Fig.3. Pomeranchuk effect at v=1 (D/ε0 =-0.6 V·nm-1). (a) The temperature dependence of resistance up to 40 K indicates a non-monotonic evolution of correlated peaks at v=1. The peak position is roughly guided by a red dashed line,while the peak magnitude R*is obtained by subtraction of a smooth background(see illustration at 10 K in the inset). (b)R* (T)for v=1,2. (c)The in-plane magnetic field shows little effect to the correlated state of v=1 at 12 K,which is also evidenced in(b).

3.5. Signature of Pomeranchuk effect at v=-3

Then we focus on the CS atv=-3. Firstly, we carried out temperature dependent measurements atD/ε0=0.32 V/nm. As shown in Fig. 4(a), the correlated feature atv=-2 is smeared out at 40 K, leaving only a broad peak as a background. The background peak can be ascribed to the VHS depicted in Fig. 2, which has been widely observed in twisted mono-bilayer graphene of various angles.[34]To identify the magnitude of the correlation peak,a simple method is adopted to remove the background peak. Inset of Fig.4(a)illustrates the subtraction process for the data at 10 K,whereR*denotes the results forv=-2,-3.Obviously,R*(v=-2)follows a general expectation that correlation peaks get stronger as thermal fluctuation diminishes. In contrast,forv=-3,R*firstly grows then below 15 K decreases sharply. The abnormal behavior below 15 K,however,is similar to the electronic Pomeranchuk effect found above atv=1 and those in TBG ofv=±1.[37,38]

To examine whether the essential ingredient of Pomeranchuk effect atv=-3 remains spin,rotatedBfields should be applied. Limited by experimental instruments, here only an in-planeBfield will be presented. As shown in Fig. 4(c),resistive peaks atv=-2,-3 both increase with strongerB(the colored curve in the inset corresponds to the dashed lines in the main figure). The former one is similar with that of twisted double bilayer graphene,[5–7,32]probably a remanence of spin-polarized bands. The latter can find its similarity withv=±1 in TBG,[37,38]where isospin fluctuation is quenched by theBfield and isospin ferromagnetism(insulating states)is restored.To further confirm the scenario of Pomeranchuk effect,we carry out the in-plane field characterization at a higher temperature but below 15 K.As shown in Fig.4(d),qualitatively similar results are observed atT=8 K.

We note that the phase boundary between an insulating isospin ferromagnetism and Fermi liquid usually shifts upon varying temperature or magnetic fields in TBG.[37,38]In other words,the filling factor of thev=-1 peak deviates away from the integer. This is not the case in AT211G atv=-3,where the peak position is pinned tov=-3 despite changing temperature andBfields. Remember in twisted trilayer graphene,[39]only the temperature can effectively shift the peak position,whereas in-planeBfield is much less effective ascribed to the ineffective coupling between isospin and magnetic field. As such,the coupling withBfields is also expected to be weak in our twisted multilayer graphene.

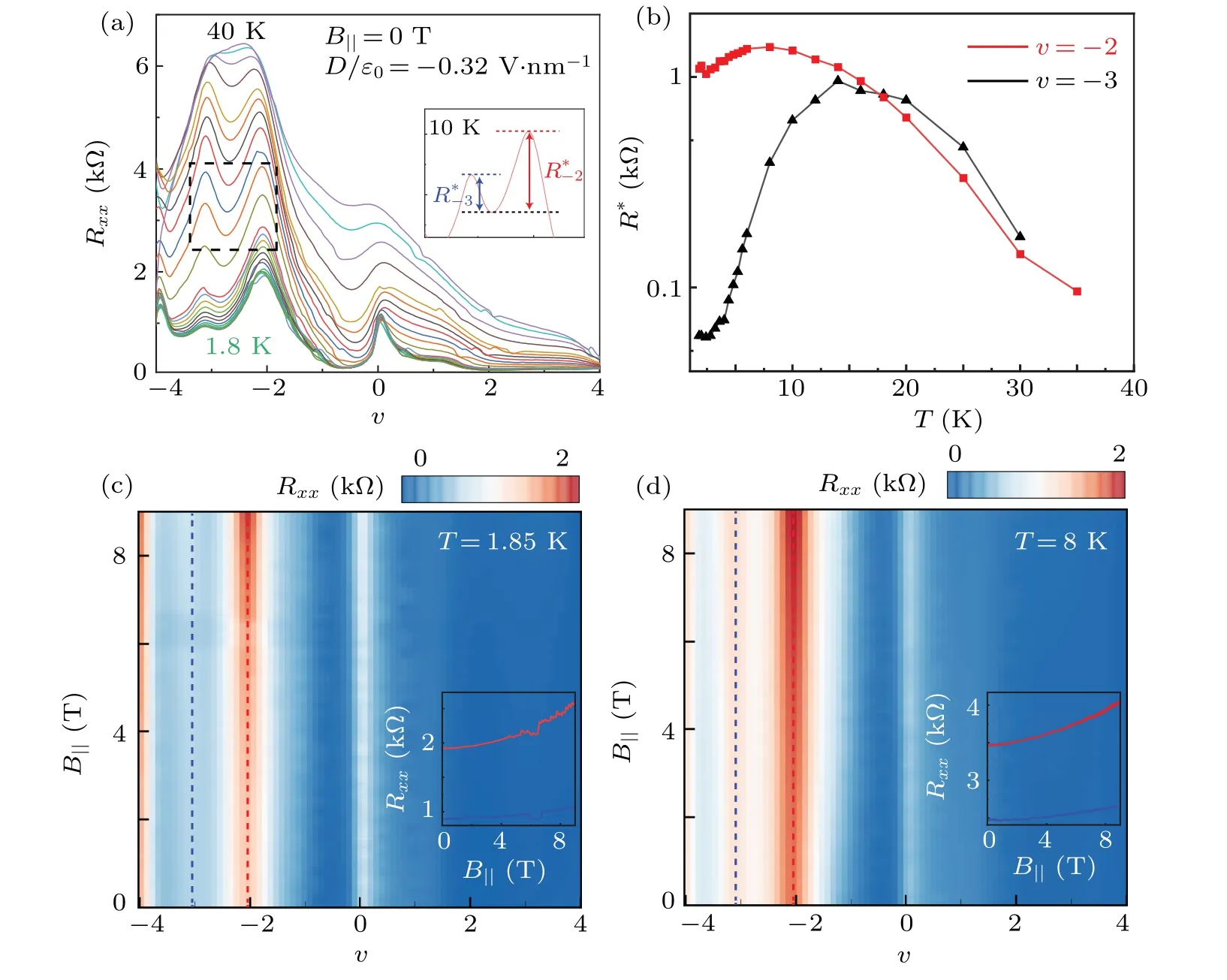
Fig.4. Signature of Pomeranchuk effect at v=-3(D/ε0=0.32 V·nm-1). (a)Temperature dependence of resistive peaks at v=-2 and-3.Inset: Definition of the effective magnitudes of correlated peaks with background removed. (b) Non-monotonic temperature dependence of correlated peaks at v=-3(c). An in-plane magnetic field enhances resistive peaks at v=-2 and-3. (d)The field enhancement is stronger at higher temperature of 8 K.

4. Conclusion and perspectives

At last, we would like to discuss a more general scenario, where the upper twist angleθ12is not equal to the lower oneθ23. Keepingθ12as the magic angle,one can varyθ23in a large range: (1) Whenθ23is relatively large, e.g.,＞5°, it was shown theoretically that the narrow band (due toθ12) is largely not hybridized by the additional dispersive band.[40]Such a decoupling behavior has been experimentally confirmed for two graphene layers.[41–43](2)With decreasingθ23, the hybridization at low energy levels is expected to increase the bandwidth and suppress electronic correlation.[40](3)When the two angles are in the same scale,moir´e-of-moir´e superlattices will emerge, bringing in novel control knobs of the band structure.[44–46]For instance, correlated states were observed in the high-order narrow band of a doubly aligned hBN–graphene–hBN heterostructure.[47]

To summarize, in an alternating twisted Bernal bilayer–monolayer–monolayer graphene of～1.74°, we found asymmetric van Hove singularities and multiple correlated states tuned by displacement fieldD. Especially atv=-3,temperature dependence characterization identified the signature of Pomeranchuk effect. Our results are expected to inspire more investigation of multilayer hybrid systems for correlated properties.

Acknowledgements

J.L. acknowledges support from the National Key R＆D Program of China (Grant Nos. 2021YFA1400100 and 2019YFA0307800),the National Natural Science Foundation of China(Grant No.11974027), and Beijing Natural Science Foundation (Grant No. Z190011). C.H. acknowledges support from the National Natural Science Foundation of China(Grant No. 62275265) and Beijing Natural Science Foundation(Grant No.4222084).